基于构型力断裂准则的裂纹与夹杂干涉问题1)
古 斌 郭宇立 李 群
(西安交通大学航天航空学院机械结构强度与振动国家重点实验室,西安710049)
基于构型力断裂准则的裂纹与夹杂干涉问题1)
古 斌 郭宇立 李 群2)
(西安交通大学航天航空学院机械结构强度与振动国家重点实验室,西安710049)
基于构型力概念提出一种可判断裂纹起裂以及裂纹扩展方向的新断裂准则.该准则假设当构型合力值达到一个临界值时裂纹开始扩展,而裂纹扩展的方向则为构型合力的矢量方向.基于此断裂准则,本文开发构型力的有限元计算方法,实现对裂纹扩展的数值模拟,并着重对工程中常见的含孔洞/夹杂结构的裂纹扩展问题展开研究.研究结果表明,基于构型力的裂纹扩展准则可以很好地预测裂纹与孔/夹杂的干涉作用,其数值模拟结果与实验结果相符,从而验证了该裂纹扩展模拟方法的有效性.通过对裂纹和夹杂(圆孔、软夹杂、硬夹杂)干涉问题的数值模拟表明,裂纹前端夹杂对裂纹的扩展具有重要影响.裂纹的扩展方向与裂纹和夹杂的相对位置、以及夹杂类型密切相关.软夹杂和圆孔会吸引裂纹向其扩展,而硬夹杂会排斥裂纹扩展,裂纹在扩展过程中会绕开硬夹杂.当裂纹与夹杂夹角较小时,夹杂对裂纹扩展的影响作用明显,当夹角较大时,夹杂对裂纹扩展的影响较小;特别当裂纹与夹杂夹角为45◦时,软夹杂和圆孔可能会抑制裂纹的扩展,使裂纹扩展发生止裂.研究结果有助于认清含孔洞/夹杂结构中的裂纹扩展或止裂问题,对于工程中的断裂问题具有重要指导意义.
构型力,断裂准则,裂纹扩展,夹杂,孔洞
引言
许多工程结构材料中通常存在着孔洞、裂纹类缺陷,对于这类结构材料断裂行为的准确预测,需要考虑孔洞和裂纹的扩展及其相互作用,研究夹杂与裂纹的相互作用问题,具有重要的工程实际意义和理论价值[1-3],国内外诸多学者针对此问题,开展了理论、数值以及实验相关研究.Atkindon[4]提出了一种包含夹杂的裂纹尖端应力强度因子的数值计算方法.Rubinstein[5]研究了宏观裂纹和微观缺陷的相互作用机制.Li等[6]采用Eshelby等效夹杂理论分析了I型裂纹与圆形夹杂体间的相互作用关系.Soh等[7]对裂纹和多缺陷介质相互作用机制进行了研究.闫相桥[8]基于单一裂纹的Bueckner原理提出了一种平面弹性介质中多孔洞多裂纹相互作用问题的数值计算方法.Mishuris等[9]采用数值模拟的方法研究了面外剪切作用下裂纹与缺陷介质的作用机制.Zhang等[10]基于分布位错法分析了有限板中裂纹与圆形夹杂的相互作用.付云伟等[11]基于相互作用直推估计法,建立一种考虑含夹杂相互作用的夹杂界面裂纹开裂模型.杨仁树等[12]采用数字激光动态焦散线方法研究了运动裂纹与圆形孔缺陷的相互作用机制.张财贵等[13]采用压缩单裂纹圆孔板确定了岩石动态起裂、扩展和止裂韧度.
裂纹与夹杂的干涉问题研究,主要借助于断裂力学的知识.虽然过去几十年,大量学者的深入研究使得断裂力学取得了长足的发展,并提出了一些经典断裂准则预测裂纹扩展,如能量释放率G[14]、应力强度因子K[15]、J积分[16-17]、裂纹尖端张开位移CTOD[18]、最大周向应力σθθ[19]和应变能密度因子S[20]等.但是由于断裂现象涉及外部载荷、介质几何构型等各方面因素,至今为止,还没有出现能够处理所有断裂问题的统一性理论,而且某些特定准则也存在着一定的局限性.其中,G,K,CTOD和J仅可以用来预测裂纹的萌生或者起裂,而无法预测裂纹的扩展方向;σθθ和S可以用来预测裂纹起裂方向,但需要一个标定距离rc来计算相关的参数,且其预测结果受该标定距离的影响.此外,在实际工程结构中,材料通常承受复杂载荷作用或者需要考虑夹杂/孔洞对裂纹的干涉作用,就需要对其复合型裂纹问题进行准确预测.许多学者对复合型断裂问题进行了理论和实验上的广泛研究,并提出了许多关于复合型断裂问题的准则.但是至今为止,对复合型裂纹的理论预测结果与实验数据之间还存在着一定的差别.
近期,材料构型力学的发展为处理复杂裂纹扩展问题提供了一种有效的手段.关于构型力的概念可以追溯到Eshelby[21]关于晶格缺陷的研究,其相关工作为随后材料构型力学的建立奠定了基础.近年来,科研工作者们在构型力的各个应用领域研究上取得了诸多进展[22-34].材料构型力学的发展对于促进断裂力学的发展和完善具有重要意义.因此,本文将首先基于材料构型力学的概念,提出一种预测裂纹起裂和扩展的统一性判定准则,该构型力断裂准则可以弥补前述准则的不足;基于构型力断裂准则,通过有限元方法对裂纹扩展过程进行数值实现,并着重研究断裂力学中的裂纹与夹杂干涉问题,分析夹杂对裂纹扩展的促进和抑制作用,最终为含复杂裂纹的材料断裂失效评估提供支撑.
1 构型力断裂准则
材料构型力学研究当材料中缺陷(夹杂、空穴、位错、裂纹、塑性区等)的构型(形状、尺寸和位置)改变时系统自由能的改变.因此,其在描述含裂纹材料的破坏行为方面具有得天独厚的优势.构型力的定义如下[21]

式中W表示应变能密度,为W对xi的显式求导,gi也称之为Eshelby构型力.此外,小变形情况下构型应力的定义如下

其中,δji为Kronecker符号,σjk为应力分量,uk,i为位移uk对坐标xi的求导,bji也称为Eshelby构型应力张量.在大变形下,构型应力可定义为
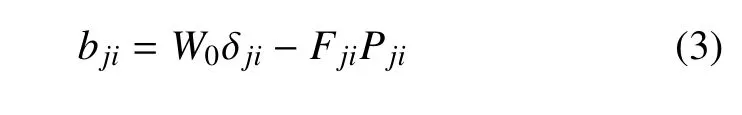
其中,W0表示应变能密度,Pji为第一Piola-Kircho ff应力分量,Fji为变形梯度.构型力与构型应力之间满足如下平衡方程

构型力是材料损伤演化的驱动力,可以作为裂纹扩展的驱动力,表征着单位厚度的无穷小单元沿xi方向滑动单位距离所产生的总势能改变量,如图1所示.
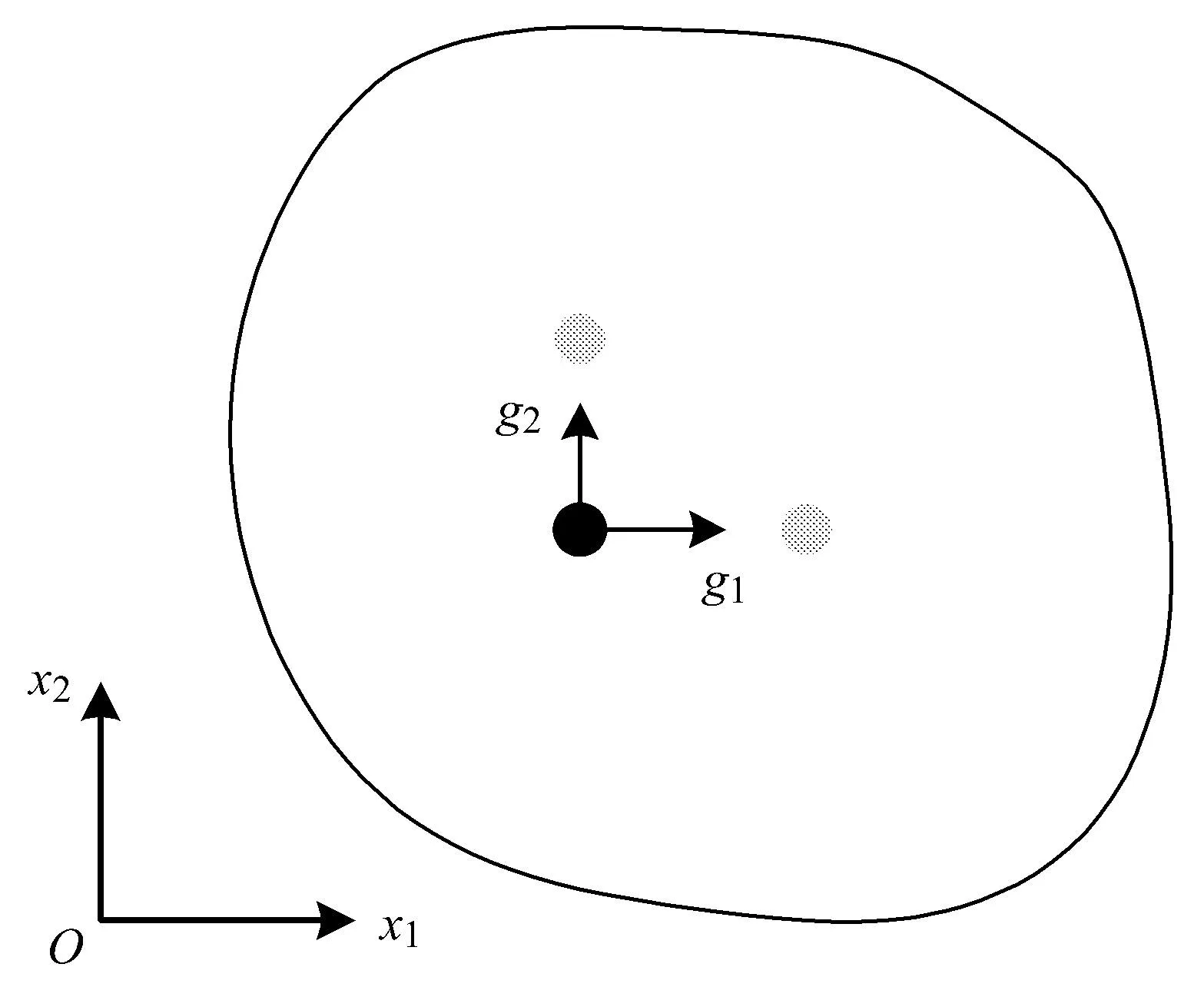
图1 平面无限小单元的滑动与构型力的关系Fig.1 The relation between the translation motion and the con fi gurational forces of planar in fi nitesimal elements
构型力的数值计算可借助于有限元方法[22],根据平衡方程式(4),首先对单元上的构型应力进行计算,进而得到单元内某个确定节点的构型力在线弹性条件下,有

其中,N表示节点对应的单元形状函数,上标e表示单元编号,βe为单元的面积.在得到某个单元内的节点构型力后,对应于K节点上构型力值则为该节点相邻的所有单元的构型力之和,即
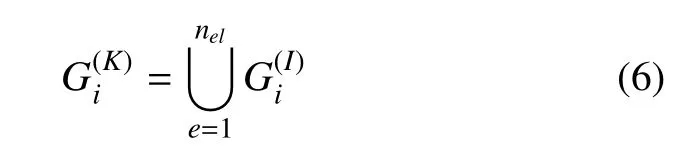
其中,nel表示节点相邻单元的个数.通过此方法,可最终得到每个单元的节点构型力数值,进而用于后面的裂纹扩展数值计算中.
而在弹塑性条件下,构型力可计算为

其中,B为塑性构型力,满足B=σ·∇εp−q∇α,α为内变量,与加载历史有关,εp为塑性应变,q是与塑性应变能密度有关的量.
基于构型力可建立相应的裂纹断裂准则,描述材料中任意裂纹的起裂和裂纹扩展方向.其描述如下:
(1)假设裂纹尖端的构型力矢量为G=(Gx,Gy),当构型力矢量(或者称为构型合力)的幅值|G|大于某一临界值时,即裂纹尖端的扩展驱动力大于材料断裂韧性时,裂纹开始扩展.即

其中Gc为材料的临界构型力断裂韧性,为材料常数,与裂纹构型和载荷无关.
(2)裂纹扩展方向假设为构型力矢量方向,其裂纹起裂角度θ可定义为

基于构型力断裂准则的优点主要有:该准则不需要定义裂尖的断裂进行区rc,即圆形损伤核,因而可以较为准确地预测裂纹起裂;该准则可同时判断起裂条件和预测裂纹扩展方向.
基于构型力断裂准则的裂纹扩展模拟算法,其流程如图2所示.首先建立含有裂纹的几何模型,划分网格,对其单元属性和材料属性进行设置.然后设置边界条件,包括力边界条件和位移边界条件.计算求解得出Eshelby构型力在裂纹尖端局部坐标系下的两个分量,根据两个分量确定Eshelby构型力合力矢量的大小,并将其与构型力临界值Gc进行比较,判断裂纹是否发生扩展,若构型力合力超过临界值Gc,裂纹继续进行扩展.根据判定准则 (9),计算裂纹偏转角θdefl,并用于建立扩展后的几何模型,沿着裂纹尖端的材料构型力合力矢量方向平移一个增量∆a,作为新的裂纹尖端,重新划分网格,求解问题,计算新的裂纹构型下的构型力合力矢量,判定是否裂纹扩展.而一旦构型力合力小于临界值Gc,则意味着裂纹扩展驱动力小于裂纹扩展阻力,裂纹发生止裂现象,此时在计算中需要跳出循环,停止计算.
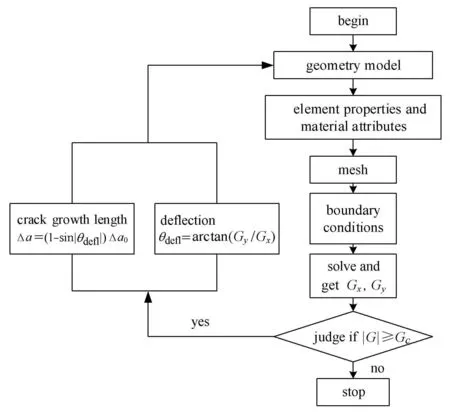
图2 基于构型力准则的裂纹扩展数值模拟流程图Fig.2 Flow diagram of numerical simulation of crack propagation based on the con fi gurational force criterion
在模拟裂纹扩展过程中,裂纹偏转角θdefl是通过构型力合力矢量与裂尖局部坐标系夹角得到.而另一个关键的控制变量就是裂纹的扩展步长∆a,为了减少不必要的数值计算量,每个子步长根据偏转角不断修正,如图 3所示,每步的扩展步长为∆a=(1−sin|θdefl|)∆a0,其中 ∆a0表示初始裂纹扩展步长,∆a为当前的扩展步长,θdefl表示裂纹尖端局部坐标系下所预测的裂纹偏转角.通过如此设置,在偏转角较小的时候,裂纹能够实现快速扩展,减少计算负担;而偏转角θdefl较大的时候,步长∆a迅速减小,便于精细观察裂纹偏转变化,提高计算准确度.另外,在数值模拟过程中,为了加快运算的速度,采用智能网格算法对裂纹可能会通过的区域采用局部加密的自由网格进行处理,并且只对裂纹尖端附近的网格进行重新划分,而远离裂尖对计算结果影响不大的区域则采用固定的网格划分.

图3 裂纹扩展子步长设置Fig.3 Substep of the crack propagation
2 裂纹和夹杂相互干涉问题的数值模拟与结果讨论
2.1 构型力准则验证
首先,通过一个含圆孔的四点弯曲梁对裂纹扩展模拟算法的可靠性进行验证,该模型常常用于验证断裂力学新准则及其相关算法的有效性,具有很强代表性.模型尺寸如图4(a)所示.初始裂纹长度为a=2.5mm,位于梁的底部中央,在裂纹附近存在一个圆形孔洞,边界条件和外载荷条件分别采用四点弯曲实验的边界条件.

图4 含圆孔四点弯曲梁的裂纹扩展模拟Fig.4 Crack propagation simulation of four-point-bending beam with circular hole
材料采用线弹性本构,弹性模量E为205GPa,泊松比υ为0.3.在计算中,其施加载荷P始终满足裂纹G>Gc的裂纹起裂条件.在本例中,不涉及失效临界载荷的判定,只是对裂纹在圆孔干涉下的扩展路径进行观察,将构型力准则计算得到的裂纹扩展数值结果与Miranda等[35]的四点弯曲实验结果进行对比.图4(b)左侧为基于构型力断裂准则的四点弯曲模型裂纹扩展路径数值模拟结果;图4(b)右侧为Miranda等的实验所得的裂纹扩展趋势.数值和实验结果表明,裂纹受孔洞的影响一直向孔的方向靠近,并最终和单孔重合,裂纹扩展结束.通过对比图4(b)中的裂纹扩展趋势,可以发现数值模拟的裂纹扩展趋势和实验结果吻合较好,这验证了通过构型力准则对裂纹扩展预测的数值模拟是可信且可行的,该准则可用于后续裂纹和孔洞干涉问题的研究中.
2.2 裂纹与孔洞干涉问题的研究
本节着重对裂纹和圆形孔洞的干涉问题进行分析,通过数值方法模拟裂纹在孔洞干涉作用下的扩展趋势,并得到Eshelby构型驱动力在裂纹扩展过程中随着裂纹扩展的变化趋势,分析和讨论裂纹扩展过程中孔洞对裂纹的屏蔽和反屏蔽作用.
如图 5所示,考虑裂纹前端存在一个圆形孔洞,α为初始裂纹与孔洞圆心和裂尖连线的夹角,裂纹尖端与圆形夹杂中心距离d=8mm,初始裂纹长度a=10mm,圆形夹杂的半径r=3mm,σ=100MPa为模型所受的均匀分布拉伸载荷,模型下端固定,假设该模型处于平面应力状态.材料采用线弹性本构,基体弹性模量E=71GPa,泊松比υ=0.33.在裂纹与夹杂干涉效应的研究中,夹杂相对于裂纹尖端的位置是一个重要参量.如图5所示,夹角α以及裂尖与圆心距离d共同决定了圆形夹杂的位置,将距离d固定,圆形夹杂的位置就可以由单一变量夹角α确定,本文的主要研究目标就是认清不同夹角α下,圆形夹杂对裂纹扩展的干涉影响.

图5 裂纹和夹杂干涉模型(单位:mm)Fig.5 Model of the crack interacting with an inclusion(unit:mm)
为了实现这一目标,分别对夹角α为0◦,15◦,30◦,45◦,60◦,75◦及 90◦的圆形孔洞进行数值模拟,观察在不同孔洞与裂纹相对位置下,裂纹扩展轨迹所受的影响,结果如图6所示.

图6 不同孔洞位置 (α =0◦,15◦,30◦,45◦,60◦,75◦及 90◦)干涉作用下裂纹的扩展趋势Fig.6 The crack propagation trend under the interaction of the hole in the di ff erent positions(α =0◦,15◦,30◦,45◦,60◦,75◦ and 90◦)
由图6可以看出,当α=0◦时,裂纹从开始扩展一直沿着它的正前方,直至与孔洞发生聚合,裂纹扩展结束;当α=15◦和30◦时,裂纹从起裂时就受到孔洞的作用,而向孔洞的方向逐渐偏转,直到裂纹与孔洞聚合,裂纹停止扩展;当α=45◦和60◦时,裂纹同样从起裂时就受到孔洞的作用向孔洞的方向偏移,偏移一定方向和距离后,裂纹扩展受到孔洞的影响力减小,裂纹绕开孔洞,一直向前继续扩展;当α=75◦和90◦时,裂纹从起裂时受到孔洞的干涉作用就非常小,裂纹存在微小偏转,裂纹呈现出完整的I型裂纹轨迹扩展,直到发生断裂为止.
裂纹尖端构型驱动力变化趋势如图7所示,为了方便对比,对不含孔洞的均质材料在相同的边界条件下的裂尖构型力进行计算.可以发现,当夹角较小时 (α=0◦,15◦,30◦),裂纹尖端的构型力在发生起裂之后迅速增大,直至发生聚合,增长的幅度远远超过没有孔洞干涉下的I型裂纹,这意味着当夹角较小时,孔洞促进裂纹的扩展.另外,随着夹角α的增大,裂尖的构型力增长幅度呈现出下降的趋势;而在夹角α=45◦和60◦时,裂尖构型力在初始增大之后,出现了短暂的下降趋势,之后再次迅速增大,对于孔洞干涉下的裂纹,其构型驱动力均小于没有孔洞干涉的纯I型的裂纹扩展构型力,说明此时孔洞的存在对裂纹扩展起到了抑制的作用;当α=75◦和90◦时,由于孔洞对于裂纹尖端的干涉作用已经非常微弱,裂尖构型力与没有孔洞干涉的纯I型裂纹扩展非常接近,孔洞的存在仅对裂纹扩展起到轻微的抑制作用.综上所述,当孔洞与裂尖的夹角α较小时(α=0◦,15◦,30◦),孔洞的存在促进了裂纹的扩展,当夹角α>45◦时,孔洞将在不同程度抑制裂纹的扩展.

图7 孔洞干涉作用下,裂尖构型力断裂参数随裂纹扩展的变化趋势Fig.7 Variation of the resultant con fi gurational force(C-force)at crack tip with crack propagation under the interaction of the hole
2.3 裂纹与软夹杂干涉问题的研究
下面,我们考虑软性夹杂对裂纹扩展轨迹的影响.裂尖附近存在弹性模量E=7GPa的均质圆形软夹杂,其弹性模量约为基体的1/10,采用与图5中相同的边界条件与外部载荷,研究7个不同夹角α下的裂纹扩展轨迹,结果如图8所示,其中黄色圆形表示均质的软夹杂材料.

图8 不同软夹杂位置 (α =0◦,15◦,30◦,45◦,60◦,75◦ 和 90◦)干涉作用下裂纹的扩展趋势Fig.8 The crack propagation trend under the interaction of the soft inclusion in the di ff erent positions(α =0◦,15◦,30◦,45◦,60◦,75◦ and 90◦)
由图8可以看出,当α=0◦时,裂纹从开始扩展到扩展结束一直沿着I型裂纹的扩展方向,即朝向软夹杂前进;α=15◦和30◦时,裂纹从起裂时就受到软夹杂的作用并向它的方向偏转,直到裂纹与软夹杂聚合;α=45◦和60◦时,裂纹从起裂时就受到软夹杂的作用发生偏转,在裂纹扩展受到软夹杂的干涉减小到一定程度后,裂纹便一直向前继续扩展;α=75◦和90◦时裂纹在起裂之后,首先向着软夹杂发生轻微的偏转,之后软夹杂对于裂尖的作用迅速减小,裂纹则继续进行着近似I型裂纹的扩展直到发生断裂为止.对比图6可以看出,软夹杂对裂纹扩展的影响趋势与孔洞模型的裂纹扩展趋势基本相似.图9给出裂纹附近存在软夹杂时,裂尖构型力随裂纹长度改变的变化趋势,可以发现,不同夹角α的软夹杂模型的裂尖构型力变化趋势与圆孔模型相似.它也很好地证明了孔洞与软夹杂的相似性.这也意味着,不管是在促进裂纹扩展的阶段还是在抑制裂纹扩展的阶段,对裂纹的干涉作用,孔洞对裂纹的干涉作用都比软夹杂要更强.
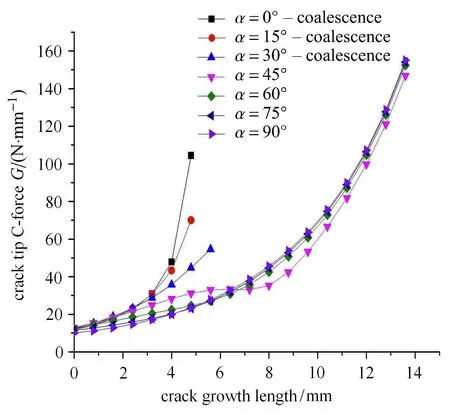
图9 软夹杂干涉作用下,裂尖构型力断裂参数随裂纹扩展的变化趋势Fig.9 Variation of the resultant con fi gurational force at crack tip with crack propagation under the interaction of the soft inclusion
2.4 裂纹与硬夹杂干涉问题的研究
图10给出硬夹杂材料对裂纹扩展趋势的影响规律.其中,取硬夹杂弹性模量E=500GPa,其弹性模量约为基体的7倍.边界条件与外部载荷不变,研究7个不同夹角α下的裂纹扩展,红色圆形表示均质线弹性硬夹杂材料.
由图10可以看出,硬夹杂对裂纹的扩展轨迹显示出与之前孔洞和软夹杂完全不同的一些现象.α=0◦时,裂纹从起裂到扩展结束一直沿着I型裂纹的轨迹扩展最终与硬夹杂聚合,这与软夹杂和孔洞的情况基本相似;但当α=15◦和30◦时,裂纹在靠近硬夹杂时受到强烈的干涉作用,绕开硬夹杂后,继续向前扩展;当α>45◦(α=45◦,60◦,75◦,90◦)时,裂纹从起裂时就受到硬夹杂的作用而选择远离硬夹杂的方向偏移,在受到硬夹杂的作用逐渐减小后,裂纹便一直向着前继续扩展.事实上,此时硬夹杂对裂纹的影响可以忽略不计,裂纹几乎是沿着纯I型裂纹扩展的方向扩展直到发生断裂.

图10 不同硬夹杂位置 (α =0◦,15◦,30◦,45◦,60◦,75◦ 和 90◦)干涉作用下裂纹的扩展趋势Fig.10 The crack propagation trend under the interaction of the hard inclusion in the di ff erent positions(α =0◦,15◦,30◦,45◦,60◦,75◦ and 90◦)
对比图6,图8和图10,可以得出如下结论,软夹杂和圆孔会吸引裂纹向其扩展,而硬夹杂会排斥裂纹扩展,裂纹在扩展过程中会绕开硬夹杂.当裂纹与夹杂夹角较小时,夹杂对裂纹扩展的影响作用明显,当夹角较大时,夹杂对裂纹扩展的影响较小;当圆形夹杂与初始裂尖的夹角α超过60◦时,不论是软夹杂、硬夹杂还是孔洞,对裂尖的影响都非常小,裂纹都会呈现出近似于I型裂纹的趋势进行扩展.
图11给出硬夹杂干涉作用下裂尖构型力随着裂纹扩展长度的变化.可以发现,当α=0◦时,硬夹杂能够明显抑制裂尖构型力的增加,直至裂纹与硬夹杂发生聚合;当α=15◦和30◦时,裂尖构型力一开始增加缓慢,之后又迅速增大,直接增长到纯I型裂纹扩展的程度,这表明,此时硬夹杂对裂纹的影响完全可以忽略当α>45◦(α=45◦,60◦,75◦,90◦)时,裂纹在起裂之后的受到轻微的抑制作用,之后便不同程度的迅速增大,直至最后曲线重合,这说明了在绕过硬夹杂后,硬夹杂对裂纹将不再有影响.观察夹角α从15◦增长到90◦,可以发现,随着夹角α的增大,硬夹杂对裂纹的抑制作用逐渐减小,对裂纹扩展趋势的影响也越小.

图11 硬夹杂干涉作用下,裂尖构型力断裂参数随裂纹扩展的变化趋势Fig.11 Variation of the resultant con fi gurational force at crack tip with crack propagation under the interaction of the hard inclusion
2.5 孔洞、软夹杂、硬夹杂对裂纹扩展影响的对比研究
为了更好地对比分析不同夹杂类型对裂纹干涉屏蔽的影响,本节将着重对孔洞、软夹杂和硬夹杂干涉下裂纹扩展轨迹,以及裂尖构型力断裂参数的影响趋势进行对比分析.其中软夹杂的弹性模量约为基体弹模的1/10,而硬夹杂弹性模量约为基体的7倍.图12和图13分别给出当夹杂与裂纹相对角度α=0◦和45◦时,其裂纹扩展趋势和裂纹尖端构型力变化趋势对比.

图12 当α=0◦时,3种不同夹杂对裂纹扩展影响Fig.12 E ff ect of three di ff erent inclusions on crack growth while α =0◦


图13 当α=45◦时,3种不同夹杂对裂纹扩展影响Fig.13 E ff ect of three di ff erent inclusions on crack growth while α=45◦
由图12(a)可以看出,当夹杂位于α=0◦时,3种夹杂模型的裂纹扩展趋势是相同的,这是模型的对称性产生的必然结果.在裂纹刚刚发生起裂时,受软夹杂与孔洞作用的裂纹,裂尖构型力比均质材料大,这说明它们会优先发生起裂.而在发生起裂之后,孔洞的作用比软夹杂增长得更为迅速.而硬夹杂与无夹杂在裂纹开始发生扩展时,裂尖构型力要小,而在起裂之后,受硬夹杂作用的裂尖构型力增长更为缓慢.显然,裂尖构型力的增长速度与裂尖附近夹杂的弹性模量相关,弹性模量越大,裂尖构型力越不容易增大,裂纹越不易扩展,更趋近于稳定的状态.
而当α=45◦时,由图13(a)可以看出,软夹杂和圆孔会吸引裂纹向其偏转,而硬夹杂会排斥裂纹,裂纹在扩展过程中会绕开硬夹杂.另一方面,在图13(b)中软夹杂和圆孔模型的构型力均为先增大再减小,然后增大,而硬夹杂模型的构型力与无夹杂情况相似,一直在增大.尤其需要注意的是,当α=45◦时,如果材料基体的断裂韧性位于软夹杂(或孔洞)曲线的两个极值点之间,那么当裂纹扩展到一定程度后,构型力值将减小,并有可能小于材料的断裂韧性Gc,此时裂纹就会出现止裂的现象.
为了更好分析孔洞夹杂对裂纹的止裂屏蔽现象,图 14给出α=45◦时,裂纹初始构型,即孔洞模型扩展4mm后的状态,假设材料断裂韧性为Gc=32N/mm,由于初始裂尖节点构型力大于临界值Gc,裂纹开始扩展,随着裂纹扩展,当裂纹扩展3.5mm时,裂尖节点构型力将小于临界值,此时裂纹将停止扩展,材料将会出现止裂现象,如图14中构型力变化趋势所示.这说明存在某些特殊的裂纹和夹杂构型,裂纹会因为圆孔的存在而发生止裂,即孔洞的存在对于材料整体来说并不意味着整体强度的下降,而会对裂纹扩展产生抑制作用,从而起到材料增韧效果.
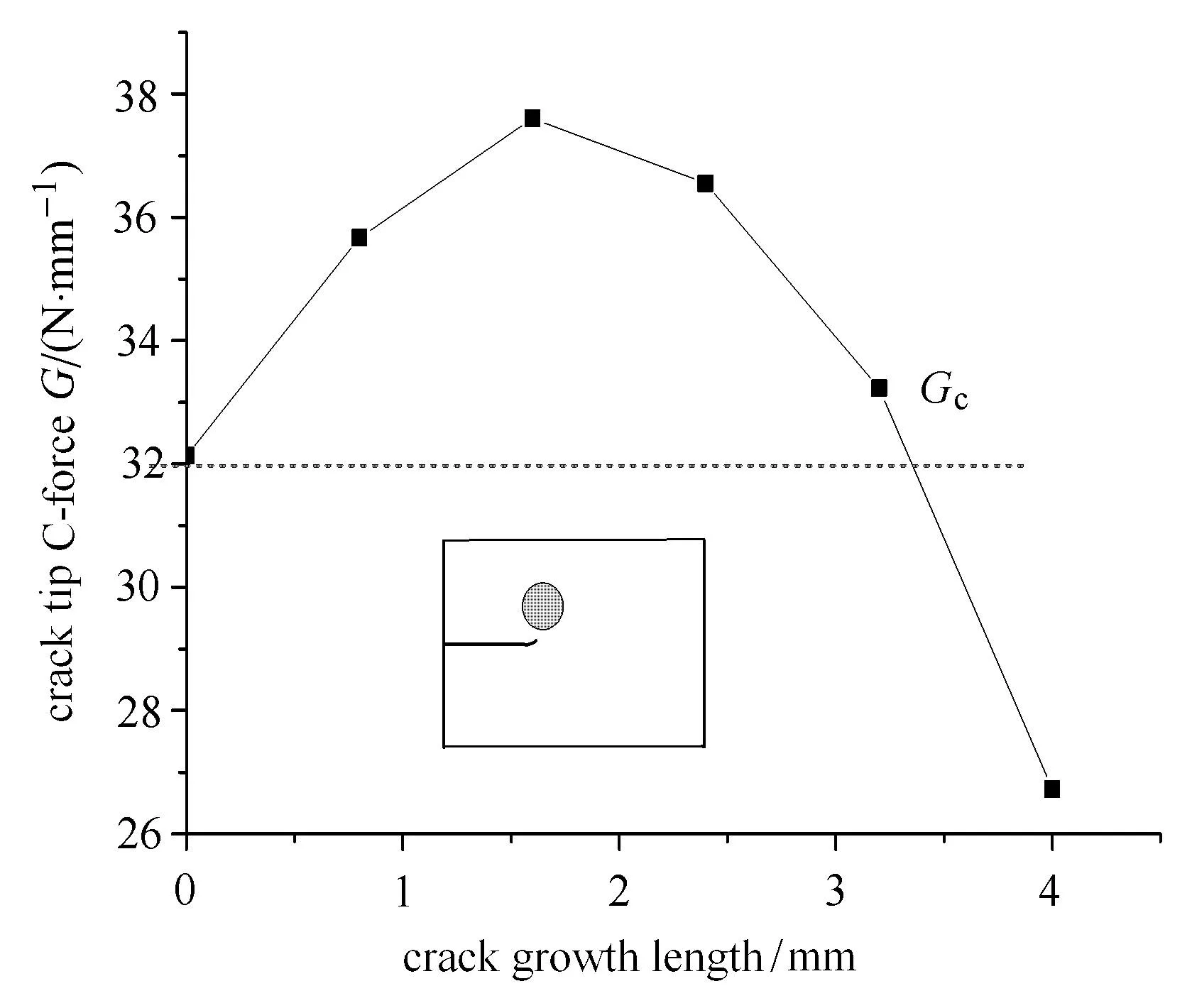
图14 α=45◦时,孔洞对于裂纹扩展的止裂分析Fig.14 Crack arresting by the hole while α =45◦
3 结论
本文基于材料构型力学概念提出一种可预测复杂裂纹起裂和扩展的构型力断裂准则,通过有限元方法对其裂纹扩展过程进行数值实现,并着重研究了裂纹和夹杂(孔洞、软夹杂和硬夹杂)的干涉屏蔽效应,主要结论如下:
(1)通过该准则对含圆孔的四点弯曲梁进行了裂纹扩展模拟,并与现有的实验结果进行了对比,构型力准则可准确预测裂纹在圆孔干涉下的扩展轨迹.对裂尖附近存在软夹杂、硬夹杂以及孔洞的模型,通过控制单一变量夹角α,表征夹杂相对裂纹的不同状态,结果发现,软夹杂和圆孔会吸引裂纹向其扩展,而硬夹杂会排斥裂纹扩展,裂纹在扩展过程中会绕开硬夹杂.
(2)通过分析三种不同类型夹杂对裂纹扩展的影响发现,当夹角α较小时,夹杂对裂纹的干涉作用非常明显,并且随着夹角α增大,夹杂对裂纹扩展的干涉作用会逐渐减小.而当圆形夹杂与初始裂尖的夹角α超过60◦时,不论是软夹杂、硬夹杂还是孔洞,对裂尖的影响都非常小.
(3)对于某些特定的初始裂纹和孔洞构型的研究发现,孔洞的存在确实可以造成裂纹止裂现象的发生.某些特定构型下,裂尖构型驱动力会出现下降的趋势,孔洞将在不同程度抑制裂纹的扩展.由此可见,孔洞的存在对于材料整体来说并不意味着整体强度的下降,反而在某些构型下会对裂纹扩展产生抑制作用,从而起到材料增韧效果.
1 Dundurs J,Mura T.Interaction between an edge dislocation and a circular inclusion.Journal of the Mechanics and Physics of Solids,1964,12(3):177-189
2 Erdogan F,Gupta GD.The inclusion problem with a crack crossing the boundary.International Journal of Fracture,1975,15(1):13-27
3 师俊平,杨成,刘协会等.夹杂对两相材料界面裂纹的影响.力学学报,2004,36(2):177-183(Shi Junping,Yang Cheng,Liu Xiehui,et al.In fl uence of inclusions on bi-materials interface crack.Acta Mechanica Sinica,2004,36(2):177-183(in Chinese))
4 Atkindon C.The interaction between a crack and a inclusion.International Journal of Engineering Science,1972,10(2):127-136
5 Rubinstein AA.Macrocrack-microdefect interaction.Journal of Applied Mechanics,1986,53(3):505-510
6 Li Z,Chen Q.Crack-inclusion interactionfor mode I crack analyzed by Eshelby equivalent inclusion method.International Journal of Fracture,2002,118(1):29-40
7 Soh AK,Yang CH.Numerical modeling of interactions between a macro-crack and a cluster of micro-defects.Engineering Fracture Mechanics,2004,71(2):193-217
8 闫相桥.孔洞裂纹问题的一种数值方法.固体力学学报,2006,27(2):198-202(Yan Xiangqiao.A numerical approach for voi crack interaction.Acta Mechanica Solida Sinica,2006,27(2):198-202(in Chinese))
9 Mishuris G,Movchan A,Movchan N,et al.Interaction of an interfacial crack with linear small defects under out-of-plane shear loading.Computational Materials Science,2012,52(1):226-230
10 Zhang J,Qu Z,Huang Q,et al.Interaction between cracks and a circular inclusion in a fi nite plate with the distributed dislocation method.Archive of Applied Mechanics,2013,83(6):861-873
11 付云伟,张龙,倪新华等.考虑夹杂相互作用的复合陶瓷夹杂界面的断裂分析.力学学报,2016,48(1):154-162(Fu Yunwei,Zhang Long,Ni Xinhua,et al.Interface cracking analysis with inclusions interaction in composite ceramic.Chinese Journal of Theoretical and Applied Mechanics,2016,48(1):154-162(in Chinese))
12 杨仁树,许鹏,岳中文等.圆孔缺陷与I型运动裂纹相互作用的试验研究.岩土力学,2016,37(6):1597-1602(Yang Renshu,Xu Peng,Yue Zhongwen,et al.Laboratory study of interaction between a circular hole defect and mode I moving crack.Rock and Soil Mechanics,2016,37(6):1597-1602(in Chinese))
13 张财贵,曹富,李炼等.采用压缩单裂纹圆孔板确定岩石动态起裂、扩展和止裂韧度.力学学报,2016,48(3):624-635(Zhang Caigui,Cao Fu,Li Lian,et al.Determination of dynamic fracture initiation,propagation,and arrest toughness of rock using SCDC specimen.Chinese Journal of Theoretical and Applied Mechanics,2016,48(3):624-635(in Chinese))
14 Griffith AA.The phenomena of rupture and fl ow in solids.Philosophical Transactions of the Royal Society of London,1921,221(2):163-197
15 Irwin GR.Analysis of stresses and strains near end of a crack traversing a plate.Journal of Applied Mechanics,1956,24:361-364
16 Cherepanov GP.The propagation of cracks in a continuous medium.Journal of Applied Mathematics&Mechanics,1967,31(3):503-512
17 Rice JR.A path independent integral and the approximate analysis of strain concentration by notch and cracks.Journal of Applied Mechanics,1968,35(2):379-386
18 Wells AA.Unstable crack propagation in metals cleavage and fast fracture.Proceedings of the Crack Propagation Symposium,1961,2:210-230
19 Hussain MA,Pu SL,Underwood J.Strain-energy-release rate for a crack under combined mode I and mode II.Fracture Analysis,1974,560:2-28
20 Sih GC.Strain-energy-density factor applied to mixed mode crack problems.International Journal of Fracture,1974,10(3):305-321
21 Eshelby JD.The elastic energy-momentum tensor.Journal of Elasticity,1975,5(3):321-335
22 Mueller R,Kolling S,Gross D.On con fi gurational forces in the context of the fi nite element method.International Journal for Numerical Methods in Engineering,2002,53(7):1557-1574
23 Kienzler R,Herrmann G.Fracture criteria based on local properties of the Eshelby tensor.Mechanics Research Communications,2002,29(6):521-527
24 Mueller R,Gross D,Maugin GA.Use of material forces in adaptive fi nite element methods.Computational Mechanics,2004,33(6):421-434
25 Carka D,Landis C.On the path-dependence of the J-integral near a stationary crack in an elastic-plastic Material.Journal of Applied Mechanics,2011,79(4):044502-044503
26 Gommerstadt BY.The J and M integrals for a cylindrical cavity in a time-harmonic wave fi eld.International Journal of Engineering Science,2013,83(10):76-84
27 Maugin GA.Sixty years of con fi gurational mechanics(1950–2010).Mechanics Research Communications,2013,50(4):39-49
28 Guo YL,Li Q.On some fundamental properties of the L-integral in plane elasticity.Acta Mechanica,2015,226(1):137-148
29 Baxevanakis KP,Giannakopoulos AE.Finite element analysis of discrete edge dislocations:Con fi gurational forces and conserved integrals.International Journal of Solids&Structures,2015,62:52-65
30 Tracy J,Waas A,Daly S.Experimental assessment of toughness in ceramic matrix composites using the J-integral with digital image correlation part I:methodology and validation.Journal of Materials Science,2015,50(13):4646-4658
31 Judt PO,Ricoeur A.A new application of M-and L-integrals for the numerical loading analysis of two interacting cracks.Journal of Applied Mathematics and Mechanics,2015,96(1):24-36
32 李群.材料构型力学及其在复杂缺陷系统中的应用.力学学报,2015,47(2):197-214(Li Qun.Material con fi gurational mechanics with application to complex defects.Chinese Journal of Theoretical and Applied Mechanics,2015,47(2):197-214(in Chinese))
33 Özenc¸K,ChinaryanG,KaliskeM.Acon fi gurationalforceapproach to model the branching phenomenon in dynamic brittle fracture.Engineering Fracture Mechanics,2016,157:26-42
34 Guo YL,Li Q.Material con fi gurational forces applied to mixed mode crack propagation.Theoretical and Applied Fracture Mechanics,2017,89:145-157
35 Miranda ACO,Meggiolaro MA,Castro JTP,et al.Fatigue life and crack path predictions in generic 2D structural components.Engineering Fracture Mechanics,2003,70(10):1259-1279
CRACK INTERACTING WITH AN INDIVIDUAL INCLUSION BY THE FRACTURE CRITERION OF CONFIGURATIONAL FORCE1)
Gu Bin Guo Yuli Li Qun2)
(State Key Laboratory for Strength and Vibration of Mechanical Structures,School of Aerospace,Xi’an Jiaotong University,Xi’an710049,China)
Based on the concept of con fi gurational force,a new fracture criterion is proposed to determine the crack initiation and the direction of crack propagation.The criterion assumes that when the resultant con fi gurational force reaches a critical value,the crack begins to grow,while the direction of the crack propagation is the vector direction of the resultant con fi gurational force.Moreover,the fi nite element method of con fi gurational force is developed to realize the numerical simulation of crack propagation.The crack propagation problem of the structure with an individual hole/inclusion in engineering is studied.The results show that the crack propagation criterion based on con fi gurational force can predict the crack growth interacting with an individual hole/inclusion well,the results of the numerical simulation are consistent with experimental results,which veri fi es the validity of the simulation method of the crack propagation.The numerical simulation of the interference between cracks and inclusions(holes,soft inclusions or hard inclusions)shows that the inclusion near tip of the crack has an important in fl uence on the propagation of the crack.The propagation direction of the crack is related to the relative position of crack and inclusion,and the type of inclusion.The soft inclusion and the circular hole attract the crack to expand,while the hard inclusion will repel the crack growth,and the crack will bypass the hard inclusion during the propagation.When the intersection angle of the crack and inclusion is small,the e ff ect of inclusion on crack propagation is obvious.The inclusion has little e ff ect on crack propagation when the angle is large.Particularly,when the angle is 45◦,and the growth of soft inclusion may suppress the crack propagation.This study can help to understand the crack propagation in the structure with voids and inclusions,and have important guiding signi fi cance for the fracture problems in engineering.
con fi gurational force,fracture criterion,crack propagation,inclusion,hole
O346.1
A doi:10.6052/0459-1879-17-209
2017–06–01 收稿,2017–08–07 录用,2017–08–11 网络版发表.
1)国家自然科学基金资助项目(11472205).
2)李群,副教授,博士生导师,主要从事断裂与损伤力学研究.E-mail:qunli@mail.xjtu.edu.cn
古斌,郭宇立,李群.基于构型力断裂准则的裂纹与夹杂干涉问题.力学学报,2017,49(6):1312-1321
Gu Bin,Guo Yuli,Li Qun.Crack interacting with an individual inclusion by the fracture criterion of con fi gurational force.Chinese Journal of Theoretical and Applied Mechanics,2017,49(6):1312-1321

