开放题:筑起“空间想象”的新时空
仲崇恒
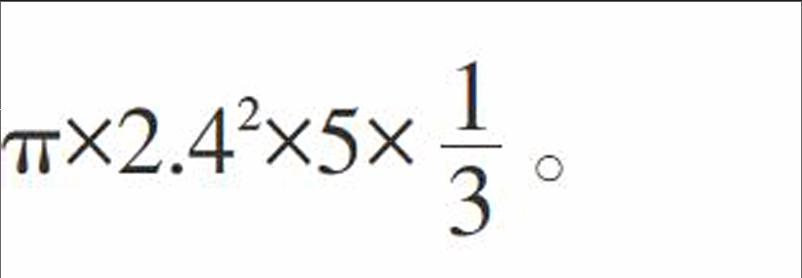
数学能力是数学教育的重要课程目标,空间想象能力是传统的三大数学能力之一。笔者在开放题评测研究中发现,开放题对学生空间想象能力有着较为直接而积极的影响,开放题教学是培养小学生空间想象能力的一条有效路径。培养学生空间想象能力,材料有很多,如图形的转换、分解、组合、辨认、概括、推理、计数、展开和折叠等。下面结合几个教学实例,来说说开放题对小学生空间想象能力培养的影响。
一、开放题,为“空间想象”奠定基石
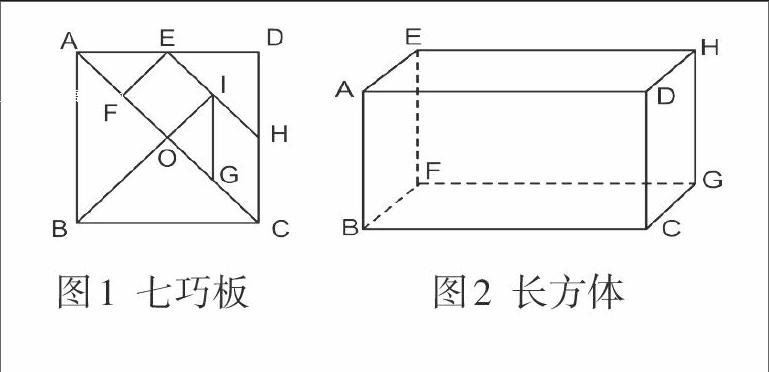
“平行和垂直”教学时,教师设计这样一道同步练习:在下列图形中,哪两条线段是相互平行的?哪两条线段是相互垂直的?
出示图1,学生小组合作探究交流后,教师追问学生有什么发现?有的发现一条直线和一组平行线的其中一条直线垂直,也与另一条直线垂直;有的发现与同一条线段垂直的两条线段是互相平行的。出示图2时,学生逐一审视长方体的十二条棱间所构成的平行或垂直。回顾图1中的发现,就有学生在图2中找到反例,从而进一步认同了“同一平面”这个判断前提。二维和三维之间的相互转换,恰是发展学生空间观念的有益举措。
一个好的开放题不是条件的多余或缺少的简单取舍,也不是问题的一而再、再而三的无序提出。开放题设计首先是从教学内容的核心知识出发,寻找思维训练的落脚点。上面习题富含空间想象元素,隐含多重维度,多种可能,相比传统的封闭习题,开放题如同一块坚实的基石,稳定性和延伸性更好,可以承载全体学生各种空间思维的不同建构。
二、开放题,为“空间想象”竖起脚手架
“长方体和正方体”单元复习时,教师课件呈现:
仓库里有以下四种规格的长方形、正方形铁皮。①长6分米,宽4分米;②长6分米,宽5分米;③长5分米,宽4分米;④边长4分米。张师傅从中选了5张铁皮,焊接成一个无盖的长方体(或正方体)水箱。你能描述一下这个水箱吗?
学生独立思考和集体交流后,教师问:怎样找出更多的,甚至所有的情况?有的学生认为:四种不同规格铁皮中有6分米、5分米、4分米三种数据,这也是焊成的水箱长宽高的长度。可以分别考虑长宽高中有三种数,或两种数,或只有一种数。有的学生认为:先定底面再选侧面,侧面的长方形铁皮和底面相连的地方长度相同。教师引导学生思考:第一种先定长宽高,第二种先定底面,两种思路都是从简到繁。接着继续探究,师问:请选择你能理解的一种思路,试一试能焊出几种不同的水箱。第二次深入交流后,教师引导:回顾过程,我们的思考和表达怎样改进才能更清晰呢?
本题条件多,答案也多,属于典型的条件和答案双开放习题。学生的不同思路呈现了两种不同的思维视角,共同点是都是从“体”出发,然后进行材料匹配。学生为了让头脑中的“体”可视化,搭建了一个个结结实实的思维脚手架,学生经历多途径、多层次的筛选、比对,通过独立思考和自主探究,理解棱、面、体之间的密切联系,进一步涵养了空间想象能力。
三、开放题,为“空间想象”架起立交桥
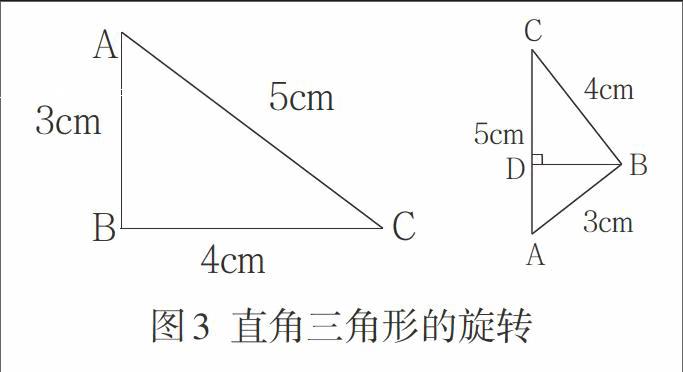
“圆锥的体积”教学时,教师出示:以直角三角形(图3)的一条边为轴,将三角形旋转一周,可以得到一个什么体?试一试画出来,然后计算它的体积。
“掌握旋转体”是中小学生空间想象能力水平的最高级。三角形有三条边,旋转后有三种情况,其中以斜边AC为轴的旋转体思维难度最大。学生通过想象,画图,讨论,交流,解决了以AB、BC两直角边为轴旋转后圆锥体积的情况。
教师:以AC为轴可以吗?想象一下能得到一个怎样的立体图形?谁能用橡皮泥把它捏出来?
两名学生捏泥,集体修正、展示后,全体学生画旋转示意图,并找出半径和高的数据。
教師:半径BD和旋转轴AC是什么关系?
学生讲解:线段BD与AC垂直,半径是2.4厘米。
教师:上下两个圆锥的高又各是多少呢?
学生讲解:不需要求出两个高。两个圆锥半径相同,底面积相同,可以合二为一,整体考虑,组合体的体积就是
上面教学中,师生互动,生生联通。整个开放题处理呈现一种立交桥结构:首先是方法孵化的立体思维。教师在学生思维遇到阻碍时,停下来,从动手捏泥到画示意图,再到联想推理,由浅入深,步步提升。其次是伙伴式的立体学习。学生们呼朋引伴,互相启发,用团队思考提升思维品质。
在空间想象能力的培养中,图形与几何是十分重要的领域,同时在数与代数、统计与概率等领域也有用武之地。比如,乘法分配律,行程问题,平均数,折线统计图等。我们认为,教与学中首先有想象的空间,然后才有空间想象。不同的学生面对一道数学题,应该有不同的思维打开方式。开放题教学不仅要在开放题的条件、问题、情境设计上下功夫,还要开放地教,开放地学。我们应该围绕这些方面进一步展开多元思考,设计出更有张力的开放题,探索更有亲和力的教学流程,帮助学生更好地理解数学,发展数学素养。
(作者单位:江苏省昆山市玉峰实验学校)

