结合非下采样Contourlet变换的改进图论MST图像分割*
廖一鹏 王卫星
(福州大学 物理与信息工程学院, 福建 福州 350108)
结合非下采样Contourlet变换的改进图论MST图像分割*
廖一鹏 王卫星
(福州大学 物理与信息工程学院, 福建 福州 350108)
为提高图论最小生成树的分割精度,保留更多边缘细节,提出了一种结合非下采样Contourlet变换(NSCT)及改进图论最小生成树(MST)的图像分割方法.首先,将图像进行NSCT分解,得到一个低频子带和多个高频方向子带,对各高频方向子带采用改进的贝叶斯萎缩阈值抑制噪声,通过模极大值检测关联边缘的像素点,结合低频子带灰度值和高频子带系数构造多尺度多方向的MST边权,并加重关联边缘的边权重;然后,从区域内部和区域间差异函数以及合并机制方面对MST分割算法进行改进,降低噪声或孤立点的影响;最后,改进和声搜索算法的“调音”策略,自适应获取MST分割算法的最优参数,得到全局最优分割.实验结果表明:与其他改进图论MST分割方法相比,文中方法的抗噪声性能好,提高了分割精度,且错分率低,所得图像边缘细节明显,分割效果较好.
图像分割;非下采样Contourlet变换;最小生成树;贝叶斯萎缩阈值;和声搜索算法;分割精度;抗噪性能
自Zahn[1]最早将图论应用于图像分割以来,图论图像分割技术因具有对数据聚类有较好的鲁棒性、对形状不敏感且能够把握住全局信息等优点,逐步成为图像分割领域中的一个新热点.2006年Sharon等[2]提出了一种分层的至上而下的图论分割方法,利用该方法,和岩石背景颜色相近的猎豹和不易分辨的草丛中的蝴蝶都能清晰地提取出来,分割效果好且效率高.2004年Felzenszwalb等[3]提出了最小生成树(MST)分割算法,该算法结果简单、分割过程充分考虑全局信息,可根据图像特性进行不同分割且效率高;但MST分割算法存在一定缺陷——边权设置只考虑灰度值,目标边缘细节易丢失;人工设置参数,参数设置偏大易产生欠分割,而参数设置过小易产生过分割,不易把握分割尺度.
为解决这一问题,Van等[4]提出结合k-均值聚类的改进MST算法实现对水果缺陷检测;王卫星等[5]提出了结合形态学分析的改进MST算法实现对粘连细胞图像分割、提出了结合抠图的改进MST算法实现模糊背景图像分割[6];李慧等[7]提出结合最小异质性合并的改进MST算法实现对遥感图像分割.但是这些改进方法都是基于具体图像目标特点来确定分割准则的,而且边权函数的改进都是单一尺度的.近几年来,多尺度几何理论的发展为图像处理提供了新的思路,在图像去噪、边缘检测、图像融合领域得到广泛应用[8- 10].Cunha等[11]提出了非下采样Contourlet变换(NSCT),继承了Contourlet变换的多方向性和各向异性的特点,而且具有平移不变性,更能表现图像的细节和几何结构,所以可在NSCT域构造多尺度多方向的MST边权,以提高像素间的差异.Oran等[12]提出的和声搜索算法(HS)对乐队调音进行模拟以实现完美和声,是一种人工智能优化算法,具有很强的全局搜索能力,是解决MST图像分割算法参数自适应优化的有效工具.
现有研究表明,可以结合NSCT分解、改进MST分割准则以及和声搜索算法来弥补传统MST分割算法的不足.为此,文中提出了一种结合非下采样Contourlet变换及改进图论最小生成树的图像分割方法.该方法首先将图像进行NSCT分解,得到多尺度多方向子带图像,高频子带通过改进贝叶斯萎缩阈值和非线性增益函数抑制噪声,结合低频子带灰度值和高频方向子带系数构造多尺度多方向的MST边权,并加重关联边缘的边权重以提高分割精度;然后从区域内部和区域间差异函数、边权函数和合并机制方面对MST分割准则进行改进,以降低噪声或孤立点的影响;最后对和声搜索算法的“调音”策略进行改进,自适应获取MST分割算法的最优参数,以得到全局最优分割.并通过实验对提出的方法的性能进行了验证.
1 NSCT域边权函数构造
1.1 非下采样Contourlet变换
Do等[13]提出的Contourlet变换对图像进行下采样,不具有平移不变性.非下采样Contourlet变换继承了Contourlet变换多尺度多方向的特性,而且分解过程中去掉下采样环节,使分解后图像具有平移不变性,能更准确地表现图像的细节和几何结构信息.NSCT分解流程如图1所示,先采用非下采样塔式滤波器组(NSPFB)对图像进行多尺度分解,得到低频子带和多个带通子带,然后再采用非下采样方向滤波器组(NSDFB)对各个带通子带进行多方向分解,得到多个不同方向的高频子带图像,最后得到一个近似图像的低频子带和多个不同尺度不同方向高频子带,而且这些子带图像的分辨率都和原始图像相同.
1.2 高频子带系数处理

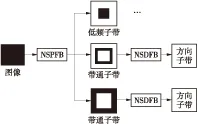
图1 非下采样Contourlet分解流程
Fig.1 Flow chart of nonsubsampled contourlet decomposition
(1)

(2)
根据贝叶斯准则,可得贝叶斯萎缩阈值:

(3)
此阈值没考虑同尺度各方向子带间的关系;图像中的边缘及细节信息对应系数的绝对值比较大,所具有的能量也比较大;而噪声比较分散,对应能量较小,系数绝对值也较小;根据能量特征改进阈值:
(4)
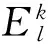

(5)

局部模极大值点,也就是边缘点,并乘上权重系数λ.
(6)
最后,该方向子带的系数处理函数为
(7)

1.3 边权函数构造
原MST算法的权重函数仅考虑灰度值的差异,没考虑像素点的空间位置,若两像素距离较远,其相关性也较弱.另外,也没考虑到边缘梯度和方向,如图2所示,红色线条代表关联图像边缘的边,黑色线条代表属于区域内部的边,原MST算法分割如图2(b),如果加大关联图像边缘的边权重(比如放大1.2倍),分割如图2(c),可提高分割精度,突出边缘细节.

图2 边权图分割
(8)
综合考虑低频子带灰度值、像素间距离、多尺度多方向高频子带系数,重新定义边权函数:
w(vm,vn)=|I(vm)-I(vn)|+d(vm,vn)+
exp[G(vm,vn]
(9)
其中,I(vm)和I(vn)分别是像素点vm和vn的在低频子带的灰度级;d(vm,vn) 代表vm和vn之间的空间欧氏距离,d(vm,vn)=[ (xm-xn)2+(ym-yn)2]1/2.
2 差异函数及合并机制改进
在NSCT域边权构造的基础上,将图像映射成一个加权图G(V,E),采用基于合并策略的Krusal算法进行分割,该算法运算效率高、分割效果好且结构简单,但存在一定缺陷,本研究改进如下.
原算法用最大边权来代表区域内部的差异,容易受噪声或孤立点影响,本研究采用平均边权来代表区域内部的差异:
(10)
而区域间的差异用最大边权和最小边权的平均值来代替,重新定义差异函数为
(11)
(12)
C1与C2是V的子集,对应于图像分割出的区域,C1与C2是两个相邻的分割区域.改进后的差异函数降低了分割敏感度,易造成欠分割,但可通过参数t来调节分割尺度.
(13)
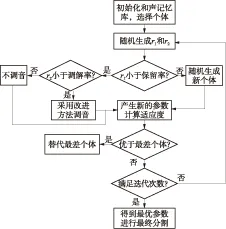
根据式(13)的判别准则,若D(C1,C2)=0,则将两区域合并一起,否则不合并.对于分割结果,如果Cα≠Cβ并且|Cα| 图像分割效果取决于参数t和q的设置,为此,把最优分割的求解转换成一个优化问题,也就是要求分割结果的类间差异和类内差异的比值最大,建立目标函数为 (14) 基本和声搜索(HS)算法对乐队调音进行模拟以实现完美和声[16],根据该思想可对优化问题进行求解.在HS算法中,候选解之间的“调音”相互独立,没有信息共享机制,而且迭代过程带宽BW保持不变,易陷入局部最优解.本研究对HS算法的“调音”策略和BW的设置进行改进,设记忆库保留概率为HMCR,音调调解率为PAR,xbest和xworst为记忆库中的最优和最差和声,xnew为将产生的新和声.随机产生r1、r2,若r1 xnew=rand(xbest-BW,xbest+BW) (15) BW=|xbest-xworst| (16) 改进了最优位置的更新策略,即对记忆库“最优美和声”xbest进行“调音”,又保留了音调调节参数BW,且随着迭代次数增加,BW慢慢缩小,能快速找到全局最优解.设置2个乐器(即t和q),初始化和声记忆库HM,产生M个初始和声,记录每个个体的适应度值,这里适应度是式(14)中H的值,算法流程如图3所示. (17) 图3 改进和声搜索算法流程图 (1) 对图像进行NSCT分解得到一个低频子带和多尺度多方向高频子带,提取低频子带灰度值,对各高频方向子带系数进行噪声抑制和模极大值检测. (2) 将图像映射为图G(V,E):构造8邻域加权图,|V|=n,|E|=m,并进行边权设定.把E中所有的权重按照升序排列,得到集合π=(O1,O2,… ,Om). (3) 初始化和声记忆库HM,产生初始和声,记录每个个体的适应度,并从HM中随机选择一组t和q. (4) 令初始分割为S0,S0=(v1,v2,…,vn),即V中每一个元素(顶点)为一类,设d为区域合并的执行次数,对于d=1,2,…,m,重复步骤(5). (6) 返回S=Sm,然后进行细小区域合并,并进行适应度计算,如果新个体优于HM中最差个体,则替换所对应的个体,否则不变. (7) 判断是否达到终止条件,如果达到最大迭代次数,转步骤(8),否则采用改进的“调音”策略产生新的个体,并转步骤(4). (8) 给分割结果的各个区域着色,并输出分割结果. 为验证本研究所提出的改进MST分割方法的性能,以Intel(R) Core(TM)i5-4 570 CPU@3.20 GH、4.00 GB(RAM)为硬件平台,以Windows 7 Matlab 2014a为仿真运行环境,结合相关图片进行测试. 在分割之前,先构造边权函数,对图像进行NSCT多尺度分解,实验对‘Peppers’图像进行2尺度分解,得到1个低通图像、高频尺度1的4个方向子带图像和高频尺度2的8个方向子带图像,如图4所示.低频反映的是图像的轮廓信息,提取各像素的灰度值和计算像素间距离.高频方向子带表现的是图像噪声、边缘和纹理细节,先进行噪声抑制,采用模极大值提取边缘系数,并相应增大其权重值,这里设λ=1.2,最后根据式(9)计算各顶点的多尺度边权. 采用文中提出的改进MST分割方法对256×256‘Peppers’图像进行分割实验,参数设置为:①t为分割控制尺度,50≤t≤600;②q为细小区域合并控制参数,这里取范围为2≤q≤80;③和声记忆库HM的和声个数M=10,和声记忆库保留概率HMCR=0.9,记忆库扰动概率PAR=0.33,实验发现迭代次数超过1 160以后不再替代最差个体,因此设置最大迭代次数N=1 200.文中方法与已有文献中的方法的分割效果如图5所示. 图4 图像NSCT分解 由图5可见,与其他MST分割效果比较,原MST算法分割结果存在大量过分割和欠分割,分割效果差;文献[4]的算法通过t均值聚类,有效解决了过分割,但是存在部分欠分割和细小区域;文献[5]的算法结合形态学对分割区域再处理,小区域合并而大区域再分割,解决了细小区域的存在,但是大区域部分存在大量过分割;文献[6]的算法通过手动调节参数t和合并参数q,并改进了合并规则,一定程度上解决了过分割和欠分割现象,但边权设置简单,大量边缘细节丢失; 文献[7]的算法采用颜色最小异质性对相邻区域进行合并,有效解决了过分割现象,但颜色相近的相邻区域易产生合并,使颜色相近的水果粘连在一起;文中方法通过改进和声搜索最优参数t和q有效解决了过分割和欠分割现象,通过NSCT域构造多尺度边权函数和加重关联边缘的边权值,使分割区域边缘细节明显,与实际目标较吻合. 图5 本文方法与已有方法的分割效果 Fig.5 Segmentation effect of proposed method and existing methods 为评价文中方法的抗噪性能,对‘Peppers’图像叠加均值为0、方差为20的高斯白噪声,采用不同的频域去噪方法进行处理,并进行比较,结果如图6所示.去噪后图像峰值信噪比(PSNR)统计如表1所示. 由图6可见,文中算法无论在信噪比,还是在平滑和边缘保持度方面,都有很大的提高.为验证去噪分割效果,分别对噪声图像6(b)和去噪后图像6(f)进行分割,效果如图6(g)和6(h),对噪声图像分割,结果出现了过分割和很多噪声孤立点,去噪处理后再分割,平滑了噪声,解决了过分割和减少了孤立噪声点,且边缘较完整.为了评价本文方法的分割效果,将文中分割方法与现有的改进MST方法进行比较,图7展示了3幅经典图像的分割效果及比对. 由图7可见,文献[4]方法存在欠分割现象,马身体部位缺失,花瓣粘连一起,无法将兔子完全分离模糊背景;同时,草地背景、兔子身体部位和花瓣周边背景区域过分割,存在孤立细小区域. 文献[5]方法对中等大小的区域分割效果好,小区域存在欠分割而大区域存在过分割现象,3幅图的背景部分过分割现象严重,花瓣内部粘连一起,兔子被分割为多个区域且眼睛部位不明显.文献[6]方法解决了上述的部分过分割和欠分割问题,但是边缘细节丢失,马与草地不能很好地分离,花瓣内部边缘缺失,兔子胡须不明显.文献[7]方法有效解决了过分割现象,但颜色相近的相邻区域易产生最小异质性合并,使颜色相近的区域粘连一起,马脚与背景合为一体,红色花瓣粘连为一体,兔子胡须被背景吸收且眼睛部位缺失.文中方法较好地解决了上述问题,很好地解决了过分割和欠分割现象,且合并了孤立细小区域,分割效果较好,结合NSCT域构造多尺度边权函数使分割结果的边缘较完整,细节更加明显. 图6 不同方法的图像去噪及分割结果 Fig.6 Image denoising and segmentation effect of different methods 表1 不同去噪方法的PSNRTable 1 PSNR of different denoise methods 图7 不同方法分割结果比较 为了进一步客观评价分割精度,对5种方法的分割精度进行比较,精度计算公式如下[6]: (18) 式中:WEpixel是期望分割结果的总边界像素点;Epixel和Upixel分别表示和期望分割结果对比,出现在期望分割结果中的边界像素点和不出现的边界像素点,即边界点的正确率与错误率;μ是惩罚系数,其值越小对错误像素点的惩罚越小,精度也越高,这里选取μ=0.3,这里期望的分割结果采用人工绘制的边界图.随机选取40幅图像,分别对原始图像和加入0均值、不同程度方差(S)的高斯白噪声图像进行分割,平均分割精度统计如表2所示. 表2 不同方法分割精度的比较Table 2 Comparison of precision of different methods 由表2可见,对原始图像分割时,相比于文献[4- 7]的方法,文中方法最少可提高3.2个百分点的分割精度;另外,随着噪声水平的增加,文献[4- 7]方法的分割精度大幅度下降,而文中方法保持较高的分割精度. 将文中方法进行实际应用,用来处理网状型裂缝之间交错复杂、线形杂乱、图像上存在很多噪声的路面网状裂缝图像,并与其他方法的处理结果进行比较,结果如图8所示。 图8 路面图像分割结果对比 由图8可见,采用文献[4- 6]中方法进行分割时因受噪声影响,存在大量过分割且裂缝细节不明显;采用文献[7]中方法进行分割时,微弱裂缝与背景颜色接近,被最小异质性合并到背景,造成一部分裂缝缺失;采用文中方法进行分割时,裂缝连续、细节明显,且裂缝完全分离背景,通过二值化、细化、毛刺去除及断点连接后与原图叠加,最终结果如图8(i)所示.采用其他传统方法检测时,检测出的裂缝不清晰,检测结果中新增了许多斑点和伪裂缝噪声,无法进一步的裂缝提取分离.由此可见,文中方法对于含大量噪声的裂缝图像在抗噪性能、分割精度方面有较大的优势. 针对图论最小生成树分割算法精度低、分割尺度无法正确把握、边缘细节信息易丢失等不足,提出了一种结合非下采样Contourlet变换和改进图论最小生成树的图像分割方法.首先将图像进行NSCT分解,高频子带通过改进贝叶斯萎缩阈值和非线性增益函数抑制噪声,通过模极大值检测关联边缘的像素点,提取低频子带灰度值和各个高频子带系数构造多尺度多方向的MST边权,并加重关联边缘的边权重;其次从区域内部和区域间差异函数、边权函数和合并机制方面对MST分割准则进行改进,降低了噪声影响和孤立细小区域;最后改进和声搜索算法,自适应获取MST分割算法的全局最优分割,有效地克服了过分割和欠分割现象.并通过实例应用对不同图像分割方法的抗噪性能、分割效果和分割精度进行比较.结果表明,该方法与其他改进MST算法相比,抗噪性能好,分割精度提高了3.2个百分点,且边缘细节明显,与实际目标较为吻合,分割效果较好.该方法也存在计算量大的问题,如何优化算法效率是下一步的研究工作. [1] ZAHN C.Graph-theoretical methods for detecting and describing gestalt clusters [J].IEEE Transactions on Com-puters,1971,C- 20:68- 86. [2] SHARON E,GALUN M,SHARON D,et al.Hierarchy and adaptivity in segmenting visual scenes [J].Nature,2006,442:810- 813. [3] FELZENSZWALB P F,HUTYENLOCHER D P.Efficient graph-based image segmentation [J].International Journal of Computer Vision,2004,59(2):167- 181. [4] VAN H P,BYUNG R L.An image segmentation approach for fruit defect detection using k-means clustering and graph-based algorithm [J]. Vietnam Journal of Computer Science,2015, 2(1):25- 33. [5] 王卫星,田利平,王悦.基于改进的图论最小生成树及骨架距离直方图分割细胞图像 [J].光学精密工程,2013,21(9):2464- 2472. WANG Wei-xing, TIAN Li-ping, WANG Yue. Segmentation of cell images based on improved graph MST and skeleton distance mapping [J].Optics and Precision Engineering, 2013, 21(9):2464- 2472. [6] 王卫星,石红玉.结合闭合解抠图及最小生成树的图论分割算法 [J].哈尔滨工业大学学报,2014,46(9):682- 687. WANG Wei-xing,SHI Hong-yu.A minimum spanning tree based image segmentation algorithm with closed form solution [J]. Journal of Harbin Institute of Technology, 2014,46(9):682- 687. [7] 李慧,唐韵玮,刘庆杰,等.一种改进的基于最小生成树的遥感影像多尺度分割方法 [J].测绘学报,2015,44(7):791- 796. LI Lui,TANG Yun-wei,LIU Qing-jie,et al. An improved algorithm based on minimum spanning tree for multiscale segmentation of remote sensing imagery [J].Acta Geodaeticaet Cartographica Sinica,2015,44(7):791- 796. [8] LIU L, JIA Z H, YANG J,et al.A medical image en-hancement method using adaptive thresholding in NSCT domain combined unsharp masking [J].International Journal of Imaging Systems and Technology,2015,25(3):199- 205. [9] ZHONG F P,MA Y Q,LI H F.Multifocus image fusion using focus measure of fractional differential and NSCT [J]. Pattern Recognition and Image Analysis,2014,24(2):234- 242. [10] 吴一全,朱丽,李立.基于NSCT和KFCM聚类的图像边缘检测方法 [J].华南理工大学学报(自然科学版),2015,43(5):59- 65. WU Yi-quan,ZHU Li, LI Li.Edge detection of images based on NSCT and KFCM [J].Journal of South China University of Technology(Natural Science Edition),2015,43(5):59- 65. [11] CUNHA A L,ZHOU J P,DO N M.The nonsubsampled contourlet transfortn:theory,design,and applications[J]. IEEE Transactions on Image Processing,2006,15(10):3089- 3101. [12] ORAN M G,MAHDAVI M.Global best harmony search [J].Applied Mathematics and Computation,2008,198(2):643- 666. [13] DO M N,VETTERLI M.The contourlet transform:an efficient directional multiresolution image representation [J].IEEE Transactions on Image Processing,2005,14(12):2091- 2106. [14] 吴一全,殷骏,戴一冕.基于人工蜂群优化的NSCT域图像模糊集增强方法 [J].华南理工大学学报(自然科学版),2015,43(1):59- 65. WU Yi-quan,YIN Jun,DAI Yi-man. Image enhancement in NSCT domain based on fuzzy sets and artificial bee colony optimization [J].Journal of South China University of Technology(Natural Science Edition),2015,43(1):59- 65. [15] TONG Y,ZHAO M R,WEI Z L,et al.Synthetic aperture radar image nonlinear enhancement algorithm based on NSCT transform [J].Physical Communication,2014,13(C):239- 243. [16] DAS S,MUKHOPADHYAY A,ROY A,et al.Exploratory power of the harmony search algorithm:analysis and improvements for global numerical optimization[J].IEEE Transactions on Systems,Man,and Cybernetics-Part B:Cybernetics,2011,41(1):89- 106. ImprovedGraphMST-BasedImageSegmentationwithNon-SubsampledContourletTransform LIAOYi-pengWANGWei-xing (College of Physics and Information Engineering, Fuzhou University, Fuzhou 350108, Fujian, China) In order to improve the segmentation accuracy of graph's minimum spanning tree and reserve more edge details, a new image segmentation method, which is on the basis of non-subsampled Contourlet transform (NSCT) and improved graph's minimum spanning tree (MST) is proposed. Firstly, an image is decomposed into a low-frequency sub-band and several high-frequency direction sub-bands through NSCT decomposition. Secondly, the high-frequency direction sub-bands are denoised according to the improved Bayes shrink threshold, and edge points are detected according to the module maxima. Then, a multi-scale multi-direction MST edge weight is constructed according to the grey value of low-frequency sub-band and the coefficients of high-frequency sub-bands, and the edge weight of edge points is increased. Moreover, MST algorithm is improved in two main aspects, one is the function of intra-regional and inter-regional differences, and the other is the re-merge mechanism after segmentation. Thus, the impact of noises or isolated points can be reduced. Finally, the optimal position adjustment strategy of harmony search is improved and adopted to find the optimal parameters of global optimal MST segmentation results adaptively. Experimental results show that, in comparison with other improved MST algorithms, the proposed method improves both anti-noise performance and segmentation accuracy, and helps obtain images with higher segmentation accuracy and better edge details. image segmentation; non-subsampled Contourlet transform; minimum spanning tree; Bayes shrink threshold; harmony search algorithm; segmentation accuracy; anti-noise performance 2016- 08- 19 国家自然科学基金资助项目(61170147,61471124,61601126) *Foundationitems: Supported by the National Natural Science Foundation of China(61170147,61471124,61601126) 廖一鹏(1982-),男,博士生,讲师,主要从事图像处理与模式识别研究.E-mail:fzu_lyp@163.com 1000- 565X(2017)07- 0143- 10 TP 391 10.3969/j.issn.1000-565X.2017.07.0203 基于改进和声搜索的最优分割
3.1 目标函数

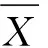
3.2 改进和声搜索最优参数
3.3 改进后MST算法的分割步骤
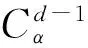
4 实验结果与分析
























5 结论

