突变信号的时幅拐点分析法*
戴屹梅 张和生 李东 齐红梅 方轲
(1.北京交通大学 电气工程学院, 北京 100044; 2.华南理工大学 软件学院, 广东 广州 510006)
突变信号的时幅拐点分析法*
戴屹梅1张和生1李东2齐红梅1方轲1
(1.北京交通大学 电气工程学院, 北京 100044; 2.华南理工大学 软件学院, 广东 广州 510006)
为解决发动机高速轴承振动数据时域信号中隐藏的突变信号难以精确时频定位的问题,提出一种突变信号的时幅拐点分析算法.该算法首先通过离散傅里叶变换对信号进行特征频率的提取,再针对该特征频率进行时移傅里叶分析,通过该频率时移傅里叶分析下的时幅拐点找出突变信号的进入时刻和消失时刻,最后通过对确定时段内的信号进行二次傅里叶分析获得该突发信号的幅值.理论分析、理论仿真和高速轴承振动数据工程仿真验证均表明,该算法能准确捕捉和提取突变信号的幅值及其在振动信号中的出现时刻和消失时刻.
突变信号;傅里叶变换;时幅拐点;频率分析
目前,在信号分析中人们普遍认为存在一种测不准关系,即:信号不能同时在时域和频域准确定位[1].传统的博里叶变换是一种基于平稳信号的全局性变换,无法反映信号的局部特征,即无法反映非平稳信号频率随时间变化的特征.
自20世纪80年代以来,随着现代信号处理理论和方法的逐步发展,对于非平稳信号的分析方法逐渐丰富起来,时频域分析法成为目前最为有效的非平稳信号处理方法.其中短时傅里叶变换(STFT)、小波变换、S变换和广义S变换等方法目前已广泛应用于非平稳信号的分析[2- 7].
短时傅里叶分析是为解决传统傅里叶分析无法获取信号的局部特征而提出来的.它通过引入一个时间窗函数来获取信号频率随时间的变化情况.文献[8]提出一种基于短时傅里叶变换的能量谱和独立分量分析的抗干扰滚动轴承包络分析方法,该方法首先对获取的信号进行STFT能量谱分析,然后进行带通滤波并提取滤波后的包络波形,再通过ICA实现包络波形分离去噪,最后通过匹配各独立分量的包络频谱和理论计算的故障特征频率来实现特征提取.
小波变换是目前使用最为广泛的时频分析方法,关于该方法的研究成果也颇为丰富,文献[9]中采用小波时频分析的方法,对航空发动机实测数据进行了分析,发现其在不同频率范围内含有不同的冲击成分;然后采用谐波小波包对不同的频带进行分解,成功地得到了其故障特征.文献[10]利用小波分解重构具有故障特征的信号,再通过Hilbert变换进行解调和细化频谱分析,能有效地提取特征频率.文献[11]中利用小波包分解对轴承的动态信号进行分析、提取特征,采用RBF神经网络进行轴承故障诊断.文献[12]对小波和Hilbert变换、小波包变换、EMD经验模态分解方法进行了深入研究,提出小波包和EMD分解相结合的故障诊断方法.该方法首先利用小波包分解去噪,重组后进行EMD分解,分析前几个IMF,提取故障脉冲的有用信息.然后找到与原始信息最相关的IMF,进行小波包分解,最后选择合适的小波包进行快速傅里叶变换,提取特征频率.
S变换和广义S变换是近年来新兴起的信号特征提取方法,该方法是小波变换和短时傅里叶变换的继承和发展.文献[13]基于STFT和连续小波变换的理论基础推导出连续S变换,并利用快速傅里叶变换(FFT)实现S变换离散化计算,仿真结果表明该方法能够提取低信噪比信号中的冲击特征.文献[14]对采集到的轴承信号进行S变换,并对变换结果s进行奇异值分解,成功提取了轴承信号特征.
为了弥补传统频谱分析在局部时域上的局限性,本研究基于快速傅里叶变换,提出了一种突变信号的时幅拐点分析方法.该方法先通过降低阈值来获取全时域下傅里叶变换的特征频率,然后针对某一个频率进行时移傅里叶分析,即在全时域(T1,T2)内,从T1时刻开始,以某一时间步长为单位逐步后移逼近T2,获取每一个时段内分析得到的频率幅值,最后将所有获得的频率幅值与分析时段形成一条时幅曲线.若该频率信号为突发信号,则可根据其时幅曲线的变化特征及其拐点来判断该信号的存在时间,最后对该频率在出现时段内进行FFT分析,获得该频率对应的信号幅值,从而较为准确地获得突发信号的特征参数.
1 时幅拐点分析算法
1.1 信号叠加的基本原理
在讨论突变信号的频率幅值在时移傅里叶分析中形成时幅拐点之前,首先分析在一信号序列上线性叠加另一个频率为k的信号序列后,该合成序列中频率k所对应的幅值变化情况.
现假设在(T1,T2)时间内,有一采样频率为Fs的信号序列q[x]={q[0],q[1],q[2],…,q[N-1]},在z时刻,q[x]上线性叠加另一序列p[x]={p[0],p[1],p[2],…,p[M-1]},其中,0≤Z≤N-M+1,M≤N.则合成后的信号序列f[x]如下式:
f[x]={q[0],q[1],…,q[Z]+p[0],q[Z+1]+
p[1],…,q[Z+M-1]+p[M-1],…,
q[N-1]}
(1)
由离散傅里叶变换可知频率k在原序列q[x]中的变换表示为式(2),其中N为原序列q[x]的总采样点数,记其变换系数为E,则有
(2)
同理,频率k在序列p[x]中的离散傅里叶变换系数表示为式(3),其中M为突变信号q[x]的总采样点数,记其变换系数为D,则有
(3)
那么,由式(1)可得频率k在合成序列f[x]中的离散傅里叶变换系数F[k]表示为式(4),记其变换系数为Y,则有
(4)
1.2 时幅拐点分析算法介绍

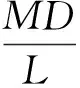
(5)
由式(5)可知E和D均为常数,其中E是频率k在原始序列中的变换系数.若原始序列不包含频率k,则E=0,此时为频率突变;若包含频率k,则E为一个正数,该值只能上下平移时幅曲线,不影响曲线的变化趋势及时幅拐点的对应时刻,此时为幅值突变.下面针对突变信号出现的不同情况进行相应分析,并找出其时幅拐点与突变信号发生时间的对应关系.
设突变信号进入到原始信号的时刻为TZ,消失时刻为Tm.则突变信号出现的时间可能有以下3种情况.
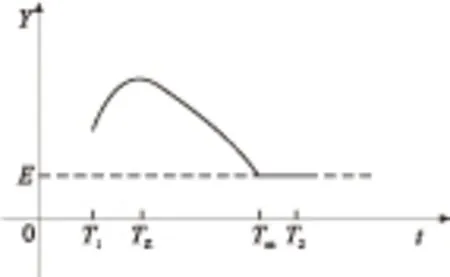
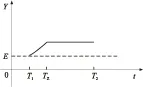
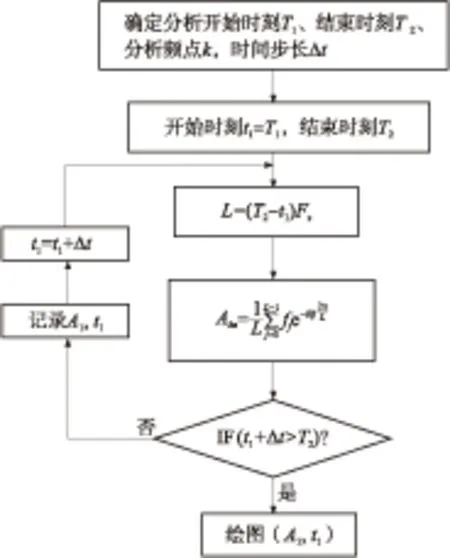
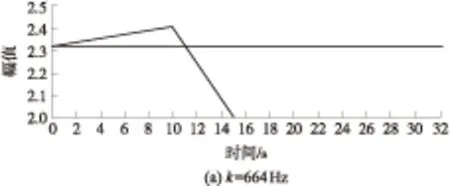
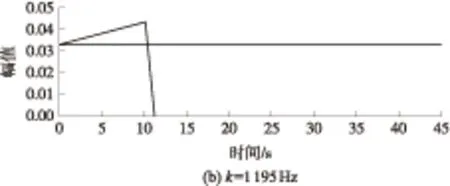
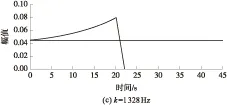
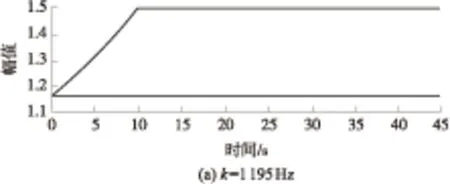
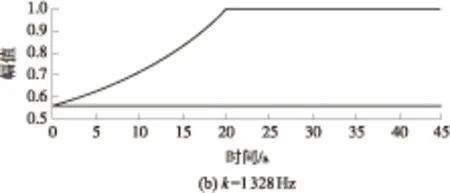
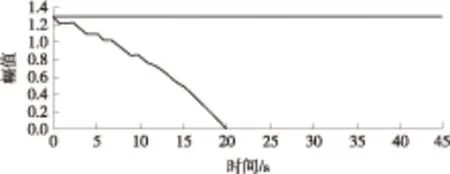
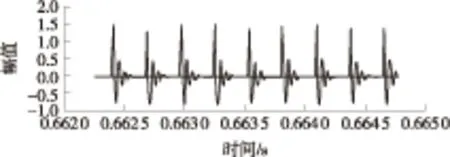
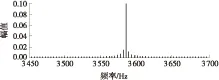
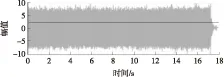
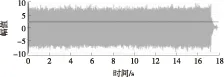
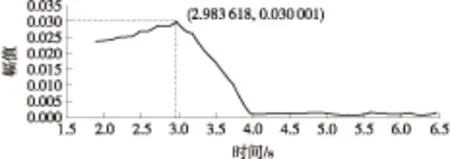
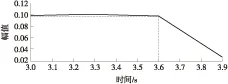
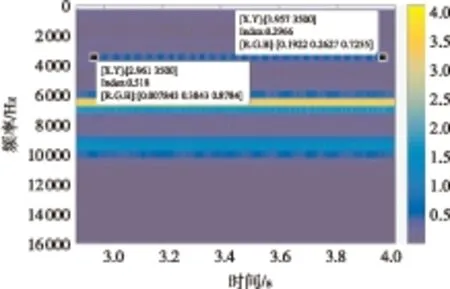
(1)TZ=T1且T1 此时由式(5)可得合成序列下频率k的幅值与递进时间之间的关系式: E,Tm (6) 由上式得出频率k的时幅曲线如图1所示,该曲线可明显看出一个时幅拐点出现在Tm时刻.在该时刻,频率幅值由递减状态进入常值状态,可判断出该频率信号的消失时刻. 图1 频率k的时幅曲线(TZ=T1且T1 (2)T1 此时由式(5)可得 (7) 由上式得出频率k的时幅曲线如图2所示,该曲线可明显看出两个时幅拐点:一个为曲线峰值,出现在TZ时刻;一个为曲线递减进入常值时刻Tm.由此可判断出该频率信号的进入时刻和消失时刻. 图2 频率k的时幅曲线(T1 (3)T1 此时由式(5)可得 (8) 由上式得出频率k的时幅曲线如图3所示,该曲线可明显看出一个时幅拐点出现在TZ时刻.在该时刻,频率幅值由递增状态进入常值状态,可判断出该频率信号的出现时刻. 图3 频率k的时幅曲线(T1 以Δt为时间步长,在(T1+nΔt,T2)时间段内逐次取信号序列fj的傅里叶变换中频率k的幅值Akn,则有 (9) 其中L为分析点数,L=N-nΔtFs;N为原序列的总采样点数,N=(T2-T1)Fs,n≤N. 实现该算法的流程图如图4所示. 图4 算法流程图Fig.4 Flow chart of the algorithm 3.1.1 仿真函数f1 该函数采样频率为12 800 Hz,采样时间50 s.f1为以下4个正弦函数的叠加: (10) 对f1的采样信号进行时移傅里叶分析,结果如图5所示. 图5 f1信号的时幅曲线Fig.5 Amplitude-time curve of signal f1 图5结果表明:①664 Hz信号的时幅曲线表现为幅值突变,符合上述图2情况,该频率的时幅曲线存在一个峰值时刻t=10 s,一个曲线递减进入常值时刻t=15 s,说明该信号的进入时刻为10 s,消失时刻为15 s;曲线最终进入一个常数状态,幅值为2,说明在该信号中始终存在一个幅值为2的664 Hz的正弦信号.②1 195 Hz信号的时幅曲线最终进入幅值为0状态,表现为频率突变,同样符合上述图2情况,存在一个峰值时刻t=10 s,一个曲线递减进入常值时刻t=12 s,说明该频率信号的进入时刻为10 s,消失时刻为12 s.③1 328 Hz信号的时幅曲线仍符合图2情况,可判断出该信号的出现时刻为20 s,消失时刻为22 s.该结果准确地捕捉到了上述第2种情况下突变信号的进入时刻和消失时刻. 3.1.2 仿真函数f2 该函数采样频率为12 800 Hz,采样时间为50 s.f2为以下3个正弦函数的叠加: (11) 对f2的采样信号进行时移傅里叶分析,结果如图6所示. 图6 f2信号的时幅曲线Fig.6 Amplitude-time curve of signal f2 图6结果表明:①1 195 Hz信号的时幅曲线符合图3情况,存在一个幅值递增进入常值时刻t=10 s,说明该信号的出现时刻为10 s;②1 328 Hz信号的时幅曲线同样符合图3情况,存在一个幅值递增进入常值时刻t=20 s,说明该信号的出现时刻为20 s.该结果准确地捕捉到了上述第3种情况下突变信号的进入时刻. 3.1.3 仿真函数f3 该函数采样频率为12 800 Hz,采样时间为50 s.f3为以下两个正弦函数的叠加: (12) 对f3的采样信号进行时移傅里叶分析,结果如图7所示. 图7结果表明:1 195 Hz信号的时幅曲线符合图1情况,存在一个幅值递减进入常值时刻t=20 s,说明该信号的消失时刻为20 s.该结果准确地捕捉到了上述第1种情况下正弦突变信号的消失时刻. 图7 f3信号的时幅曲线Fig.7 Amplitude-time curve of signal f3 根据参考资料[9],可以构造以下函数来仿真轴承外圈单点故障特征频率时域波形: (13) 图8 外圈单点故障特征波形Fig.8 Characteristic waveform of single point fault of outer ring 对该函数进行128 000 Hz采样,采样时间为1 s,其频谱图如图9所示.从图上可看出,基频3 585 Hz的幅值为0.1. 图9 外圈单点故障频谱图Fig.9 Single point fault spectrum of outer ring 采用某火箭发动机高速滚动轴承正常试验振动数据,将仿真波形采样数据从第378 952个数据点叠加到真实的试验数据上,构成一个新的数据序列.真实数据与合成数据的波形如图10和图11所示,从图中可以看出,在时域上很难发现该信号,而直接进行频谱分析又会大大削弱该频率信号的幅值. 针对外圈单点故障特征波形的基频3 585 Hz,采用文中提出的分析方法对合成数据进行定频分析,分析结果如图12所示,显然符合上述图2情况,可以找出该频率出现和消失的时点分别为2.983 61 s和3.983 61 s. 图10 真实试验数据的时域图Fig.10 Time domain figure of real test data 图11 合成数据的时域图Fig.11 Time domain figure of synthetic data 图12 合成数据的时幅曲线Fig.12 Amplitude-time curve of synthetic data 在找出频率的存在时间后,在该时间区域内进行二次频谱分析便可得到该信号的实际幅值.根据图12的结果可知,3 585 Hz信号出现在2.983 61 s到3.983 61 s之间.对2.983 61 s到3.983 61 s之间的数据进行频谱分析则可得到信号的实际幅值,结果如图13所示,从图中可以看出该信号的幅值为0.1,与图9添加前的信号幅值相等. 图13 合成数据的区间分析Fig.13 Interval analysis of synthetic data 用Matlab中“cmor5- 5”对3.2节的工程数据采用‘db4’三层分解,取第三层低频段数据进行小波变换,得出的时频图如图14所示. 由图14可见,在2.961~3.957 s时间段内出现了一个在3 250~3 750 Hz频带范围内的频率.将该时间段进行局部放大,可以看出该条纹呈齿轮状,说明信号幅值是周期变化的. 与时幅拐点分析方法相比,两者都准确地捕获到突发信号的出现和消失时刻,区别在于时幅拐点分析的是一个频率,小波分析的是一个频带.在突发信号的幅值确定方面,小波分析方法并不能直接获取该突发信号的幅值.图中通过颜色来区分的仅代表该突发信号与小波基函数的相关程度,不代表频率幅值情况. 图14 小波分析频谱图Fig.14 Wavelet transform spectrum 针对时域信号中突变信号难以准确定位的问题,提出一种突变信号的时幅拐点分析算法.该算法弥补了传统频谱分析在局部时域上的局限性,与短时傅里叶变换和小波变换相比,它以充足的信息量作为傅里叶变换的基础,对单频率进行时移傅里叶分析,获得其时幅曲线,通过时幅曲线拐点能较为准确地判别特征频率信号的出现与消失时刻,对分析时段内的信号进行二次傅里叶分析可获得较为准确的信号幅值.最后通过理论分析、理论仿真和工程仿真验证了文中模型的精确性以及时幅拐点算法在捕捉突变信号中的有效性. [1] Ingrid Daubechies.小波十讲 [M].李健平,译.北京:国防工业出版社,2011:1- 5. [2] 隆军,吴金强.STFT和HHT在风力机轴承故障诊断中的应用 [J].噪声与振动控制,2013(4):219- 222. LONG Jun,WU Jin-qiang.Application of short time fourier transform and hilbert-huang transform in fault diagnosis of rolling bearing of windmill [J].Noise and Vibration Control,2013(4):219- 222. [3] 苏文胜,王奉涛,朱泓,等.基于小波包样本熵的滚动轴承故障特征提取 [J].振动、测试与诊断,2011,31(2):162- 166. SU Wen-sheng,WANG Feng-tao,ZHU Hong,et al.Feature extraction rolling element bearing fault using wavelet packet sample entropy [J].Journal of Vibration Measurement & Diagnosis,2011,31(2):162- 166. [4] 苏涛,夏均忠,李树珉,等.基于小波降噪和希尔伯特黄变换的滚动轴承故障特征提取 [J].军事交通学院学报,2014,16(3):52- 56. SU Tao,XIA Jun-zhong,LI Shu-min,et al.Fault features extraction of rolling bearing based on wavelet De-noising and HHT [J].Journal of Military Transportation University,2014,16 (3):52- 56. [5] 张云鹏,盖强.S变换在滚动轴承故障诊断上的应用 [J].应用科技,2011,38(7):26- 28. ZHANG Yun-peng,GAI Qiang.Application of S-Transform in rolling bearing fault diagnosis [J].Applied Science and Technology,2011,38(7):26- 28. [6] 陈换过,易永余,陈文华,等.基于广义S变换的齿轮箱轴承故障诊断方法 [J].中国机械工程,2017,28(1):51- 56. CHEN Huan-guo,YI Yong-yu,CHEN Wen-hua,et al.Fault diagnosis method of gearbox bearings based on gene-ralized S-transform [J].China Mechanical Engineering,2017,28(1): 51- 56. [7] 张云强,张培林,吴定海,等.基于最优广义S变换和脉冲耦合神经网络的轴承故障诊断 [J].振动与冲击,2015,34(9):26- 31. ZAHNG Yun-qiang,ZHANG Pei-lin,WU Ding-hai,et al.Bearing fault diagnosis based on optimal generalized S transform and pulse couped neural network [J].Journal of Vibration and Shock,2015,34(9):26- 31. [8] 唐先广,郭瑜,丁彦春,等.基于短时傅里叶变换和独立分量分析的滚动轴承包络分析 [J].机械强度,2012,34(1):5- 9. TANG Xian-guang,GUO Yu,DING Yan-chun,et al.App-lication of rolling element bearing envelope analysis based on short time fourier transition and Independent components analysis [J].Journal of Mechanical Strength,2012,34(1):5- 9. [9] 何卫锋,程礼,李应红.某双转子发动机冲击振动的分频小波提取与故障分析 [J].航空动力学报,2006,21(2):361- 365. HE Wei-feng,CHENG Li,LI Ying-hong.Wavelet extraction of Impact vibration frequency component and fault analysis for a twine spool aero-engine [J].Journal of Aerospace Power,2006,21(2):361- 365. [10] 陈东雷.高速牵引电机轴承试验与测试研究 [D].北京:北京交通大学,2009. [11] 吴德华,鲁五一,熊红云,等.基于RBF神经网络的航空发动机轴承故障诊断 [J].长沙航空职业技术学院学报,2005,5(2):23- 26. WU De-hua,LU Wu-yi,XIONG Hong-yun,et al.Aeroplane engine bearing fault testing by RBF neural network [J].Journal of Changsha Aeronautical Vocational & Technical College,2005,5(2):23- 26. [12] 吴勇.基于小波分析的高速牵引电机轴承故障诊断研究 [D].北京:北京交通大学,2011. [13] 郭远晶,魏燕定,周晓军,等.S变换用于滚动轴承故障信号冲击特征提取 [J].振动、测试与诊断,2014,34(5):818- 822. GUO Yuan-jing,WEI Yan-ding,ZHOU Xiao-jun,et al.Impact feature extraction from rolling bearing fault signal by S transform [J].Journal of Vibration Measurement & Diagnosis,2014,34(5):818- 822. [14] 徐宏武,范玉刚,吴建德.基于S变换特征提取和隐马尔科夫模型的故障诊断方法研究 [J].计算机与应用化学,2016,33(2):152- 156. XU Hong-wu,FAN Yu-gang,WU Jian-de.The research on fault diagnosis method based on feature extraction by S-transform and hidden Markov Model [J].Computers and Applied Chemistry,2016,33(2):152- 156. [15] 杨国安.滚动轴承故障诊断实用技术 [M].北京: 中国石化出版社,2012:32- 54. AMethodtoAnalyzeAmplitude-TimeInflectionPointofMutationSignals DAIYi-mei1ZHANGHe-sheng1LIDong2QIHong-mei1FANGKe1 (1. School of Electrical Engineering, Beijing Jiaotong University, Beijing 100044, China; 2. School of Software Engineering, South China University of Technology, Guangzhou 510640, Guangdong, China) As the mutation signals hidden in the vibration data of engine’s high-speed bearing are difficult to pinpoint in time domain, a new algorithm to obtain the amplitude-time inflection point of mutation signals is proposed. Firstly, the characteristic frequency of the signal is extracted via discrete Fourier transform. Secondly, a time-lapse Fourier analysis of the frequency is executed, which helps obtain amplitude-time inflection points. Then, the appearing and disappearing moments of the mutation signal are discovered according to the inflection points. Finally, the amplitude of the mutation signal is obtained via the quadratic Fourier analysis of the signal in a certain period. The results of theoretical analysis, theoretical simulation and engineering simulation all indicate that the proposed algorithm can capture the amplitude of mutation signals accurately, and obtain the appearing and disappearing moments of mutation signals in vibration data. mutation signal; Fourier transform; amplitude-time inflection point; frequency analysis 2016- 10- 28 广东省科技计划项目(2015B010103002,2016B09098062);北京航天动力研究所委托项目(E14GY500010) *Foundationitems: Supported by the Science and Technology Plan of Guangdong Province(2015B010103002,2016B09098062) 戴屹梅(1970-),女,博士生,高级工程师,主要从事信号采集、数值分析、高速轴承故障诊断等研究.E-mail:daiym@spacechina.com 1000- 565X(2017)07- 0077- 07 TH 133.3 10.3969/j.issn.1000-565X.2017.07.011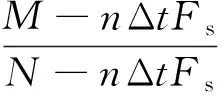

2 数学模型
3 仿真校验
3.1 理论仿真
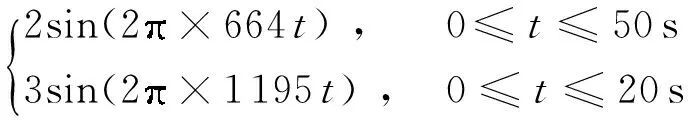
3.2 工程仿真


4 与小波分析的比较
5 结论

