完备Brouwerian格上@-Fuzzy关系方程有唯一解的判别法

夏 嫦

(成都文理学院 数学与统计学院, 四川 成都 610400)

完备Brouwerian格上@-Fuzzy关系方程有唯一解的判别法

夏 嫦

(成都文理学院 数学与统计学院, 四川 成都 610400)

在完备Brouwerian格上讨论了@-Fuzzy(其中@表示inf-α合成)关系方程有唯一解的问题，首先定义了@-Fuzzy关系方程的特征矩阵，然后利用特征矩阵给出了方程有唯一解的判别法.

完备Brouwerian格； 交既约元； @-Fuzzy关系方程； 极大解； 唯一解

自从1976年E. Sanchez[1]介绍了max-min合成Fuzzy关系方程的理论后,许多研究工作者进一步扩大了此理论的研究，如文献[2-7]． 1985年，A. Di Nola等[8]引入了@-Fuzzy关系方程并找到了方程的最小解，得到了@-Fuzzy关系方程有解的一个充要条件，即一个@-Fuzzy关系方程有解当且仅当方程有最小解．1989年，A. Di Nola等[9]在线性格上讨论了@-Fuzzy关系方程并构造出其极大解．人们发现定义在完备Brouwerian格上的@-Fuzzy关系方程的解集通常是一交半格,解集是由一个个区间构成的[9]．因此，如果能够证明对@-Fuzzy关系方程的每个解至少存在一个大于或等于它的极大解，且这样的极大解只有有限个，那么方程的整个解集就可以确定．因此，围绕定义在完备Brouwerian格上的@-Fuzzy关系方程的解集中的每个解是否存在一个大于或等于它的极大解问题，研究者们做了大量的工作[10]．模糊关系方程的极小(大)解的求解问题与矩阵的覆盖问题密切相关[11],熊清泉[12]讨论了[0,1]格上inf-IT合成模糊关系方程极大解与特征矩阵的覆盖问题的关系，并通过特征矩阵的覆盖问题获得方程有唯一(极大)解的充要条件．之前的讨论多集中在[0,1]格上，本文在完备Brouwerian格上讨论@-Fuzzy关系方程有唯一解的判别问题.

1 预备知识

设A=(aij)I×J为完备Brouwerian格上的矩阵,B=(bi)i∈I为完备Brouwerian格上的一列常向量，X=(xj)j∈J为取值于完备Brouwerian格上的一未知向量，I、J为有限集，则称

A@X=B,

(1)

即

为@-Fuzzy有限关系方程，其中,“@”表示inf-α合成．

本文研究方程(1)有唯一解的判别方法，并记

χ*={x∈χ:x是χ的极大元}.

定义1.1[11]设(P,≤)为一个偏序集且X⊆P，如果p∈X，不存在x∈X使得xgt;p，则称p为X的极大元.

注1.1由定义1.1，x*∈χ是χ的极大元当且仅当∀x∈χ，x≥x*蕴含x=x*.

定义1.2设A=(aij)n×m,B=(bij)m×k，定义A⊙B=(dij)n×k如下：

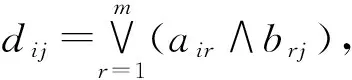
定义1.3[13]设L为格，任取x,y,b∈L，如果b=x∧y蕴含x=b或x=a，则称b为格L的交既约元.

引理1.1[14]设L为完备Brouwerian格，∀a,b∈L,aαb≥b.

引理1.2[10]aαx=b有解当且仅当a∧b是解.进一步，当aαx=b有解时，x∈[a∧b,b].

引理1.3[9]χ≠Ø当且仅当AT⊙B∈χ.进一步，AT⊙B是方程(1)的最小解.

以下均假设∀i∈I,bi为交既约元.

引理1.4如果x=(xj)j∈J∈χ当且仅当∀i∈I,j∈J，有aijαxj≤bi，并且对每一个i∈I，存在j∈J使得aijαxj=bi.

证明由于∀i∈I,bi为交既约元，结论显然成立.

2 解的唯一性

定义2.1对于方程(1)的最小解x*=(xj*)j∈J，方程(1)的特征矩阵Q=(qij)I×J定义如下：

∀i∈I,j∈J.

(2)

特征矩阵Q中的每个元qij中的值xj∈[xj*,bi]满足aijαxj*=bi.

由引理1.4和定义2.1容易得到以下定理.

定理2.1χ≠Ø当且仅当Q的每一行都不全是空集.

证明必要性 设χ≠Ø，则方程有最小解x*，由引理1.4知∀i∈I,存在j∈J使aijαxj*=bi,则由定义2.1知qij=[xj*,bi],即qij≠Ø，故Q的每一行都不全是空集.

充分性 设Q的每一行都不全是空集，则∀i∈I,存在j0∈J，使qij0=[xj0*,bi]≠Ø，且aij0αxj0*=bi，令y=(yj)j∈J满足：

则y∈χ，即χ≠Ø.

例2.1设格L=([0,1]2,∨,∧),任取〈c1,c2〉,〈d1,d2〉∈L,定义〈c1,c2〉≤〈d1,d2〉当且仅当c1≤d1,c2≤d2；

〈c1,c2〉∧〈d1,d2〉=〈c1∧c2,d1∧d2〉,
〈c1,c2〉∨〈d1,d2〉=〈c1∨c2,d1∨d2〉,
〈c1,c2〉α〈d1,d2〉=〈c1αc2,d1αd2〉.

任取e,f∈L，记[e,f]={x∈L:elt;xlt;f}.考虑方程A@X=B,其中

b1=〈1,0.4〉,b2=〈0.4,1〉均为交既约元.该方程有解，且最小解为

因此特征矩阵为

Q=

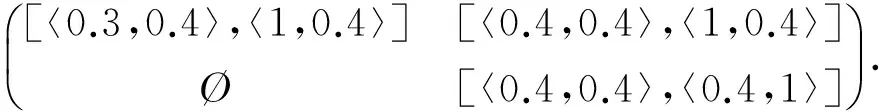
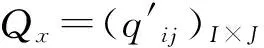
(3)

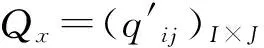
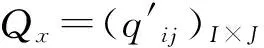
定义2.2若对所有的j∈J，都有qi2j⊆qi1j，则说Q的第i1行控制第i2行.易知，若Q的第i1行控制第i2行,则bi2≤bi1.由引理2.1可知，若Q的一个行控制了其他一个或几个不全为0的行，则该行可被排除掉.

定义2.3∀j∈J,若存在i∈I，使qij是Q的第i行唯一一个非空集，则称j在核ker(Q)中，即j∈ker(Q)={j∈J|qij为Q的第i行的唯一一个非空集}.

对∀j∈J，设Mj={i∈I|qij为Q的第i行的唯一一个非空集}，显然Mj≠Ø当且仅当j∈ker(Q).∀j∈J，设

(4)

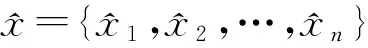
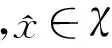
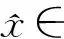
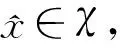
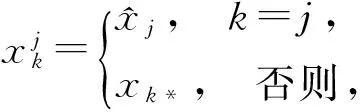
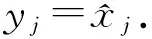
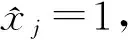
推论2.1设χ≠Ø，则(1)式有唯一极大解当且仅当∀j∈J,j∈ker(Q).

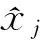
而且，(1)式有唯一解当且仅当∀j∈J,j∈ker(Q).

由定理2.1和推论2.2容易得到下面定理：

定理2.3设χ≠Ø，则Q的每一行恰有一个非空元素且每个非空元素为单点当且仅当(1)式的解唯一.

例2.2设L为例2.1中定义的格，考虑方程A@X=B,其中

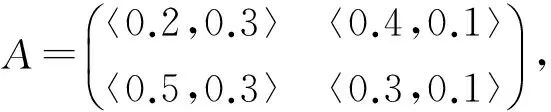
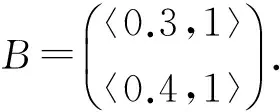
b1=〈0.3,1〉,b2=〈0.4,1〉均为交既约元.该方程有解，且最小解为

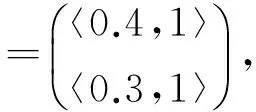
因此特征矩阵为

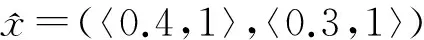
[1] SANCHES E. Resolution of composite fuzzy relation equations[J]. Inform and Control,1997,30(6):38-48.

[2] 王学平,张三华,冯山. 完备格Brouwerian上Fuzzy关系方程极小解存在的一个充分条件[J]. 四川师范大学学报(自然科学版),1999,22(6):627-630.

[3] WANG X P. Method of solution to fuzzy relation equations in a complete Brouwerian lattice[J]. Fuzzy Sets and Systems,2001,120(3):409-414.

[4] 王学平. 完备Brouwerian格上Fuzzy关系方程有极小解的条件[J]. 数学进展,2002,31(3):220-228.

[5] WANG X P. Infinite fuzzy relational equations in a complete Brouwerian lattice[J]. Indian J Pure Appl Math,2002,33:87-95.

[6] WANG X P. Infinite fuzzy relational equations on a complete Brouwerian lattice[J]. Fuzzy Sets and Systems,2003,13(3)8:657-666.

[7] WANG X P, XIONG Q Q. The solution set of a fuzzy relational equation with sup-conjunctor compsition in a complete lattice[J]. Fuzzy Sets and Systems,2005,153(2):249-260.

[8] DI NOLA A. Fuzzy relation equations and algorithms inference mechanism in expert systems[C]//GUPTA M M, KANDEL A, BANDLER W, et al. Approximate Reasoning in Expert Systems. Amsterdam:Elsevier Science Publishers,1985,34:355-367.

[9] DI NOLA A. Fuzzy Relation Equations and Their Applications to Knowledge Engineering[M]. Dordrecht:Kluwer Academic Publishers,1989.

[10] LI Y M, WANG X P. Necessary and sufficient congditions for existence of maximal solutions for inf-@ composite fuzzy relation equations[J]. Comput Math Appl,2008,55:961-1973.

[11] CHEN L, WANG P P. Fuzzy relation equations(I): the general and specialized solving algorithms[J]. Soft Computing,2002,45(6):428-435.

[12] 熊清泉. 完备Brouwer格上几类模糊关系方程的求解[D]. 成都:四川师范大学,2012.

[13] GRAWLEY P, DDWORTH R P. Algebraic Theory of Lattices[M]. NJ:Prentice-Hall, Englewood Cliffs,1973.

[14] BIRKHOFF G. Lattice Theory[M]. 3rd ed. Providence RI:Am Math Soc,1979.

2010MSC:03E72； 06D72； 08A72

(编辑 周 俊)

The Determinant Method That @-Fuzzy Relational Equation on Complete Brouwerian Lattices Has a Unique Solution

XIA Chang

(CollegeofMathematicsandStatistics,ChengduCollegeofArtsandSciences,Chengdu610400,Sichuan)

In this paper we study the unique solution problem for the @-fuzzy relational equation on complete Brouwerian Lattices, where @ denotes inf-αcomposition. We firstly define a characteristic matrix of the @-fuzzy relational equation and then use it to give a criteria for the existence of the unique solution of the equation.

complete Brouwerian lattices; meet irreducible element; @-fuzzy relational equation; maximmal solution; unique solution

O159

A

1001-8395(2017)06-0787-04

10.3969/j.issn.1001-8395.2017.06.013

2017-01-10

国家自然科学基金(61273242)

夏 嫦(1981—)，女，讲师,主要从事格上关系方程的研究，E-mail：028xiachang@163.com