基于二维非齐次泊松过程的风险度量研究——以中兴通讯日收益数据为例

于 健， 徐美萍

(1. 北京建筑大学 理学院, 北京 102616； 2. 北京工商大学 理学院, 北京 100048)

基于二维非齐次泊松过程的风险度量研究
——以中兴通讯日收益数据为例

于 健1， 徐美萍2*

(1. 北京建筑大学 理学院, 北京 102616； 2. 北京工商大学 理学院, 北京 100048)

以具有厚尾的中兴通讯日收益数据为例,考虑年度趋势和波动率等影响因素,应用二维非齐次泊松过程对超出时刻和相伴损失进行拟合,结果显示非齐次泊松过程的拟合表现明显优于其特殊情形齐次泊松过程,说明影响因素起了显著作用.模型的合理性通过模型校验予以阐明,并计算了拟合模型下的在值风险和相伴预期损失.研究表明,使用非齐次泊松模型可以更好地捕捉极端数据信息,得到更精确的风险度量估计值,为投资者规避损失提供借鉴.

超阈值模型; 二维非齐次泊松过程; 在值风险; 预期损失

在值风险(VaR)是业界用做风险度量的一个重要工具,但它有两方面不足:第一,它没有考虑一旦非正常情况出现(即损失超过VaR)时极端损失的严重程度,可能低估实际损失;第二,它不满足次可加性质,违背了以分散化投资来降低投资组合风险的初衷.为此另一个风险度量工具应运而生,它就是预期损失(ES).由于ES在VaR的基础上进一步考虑了出现极端情况时的平均损失程度且满足次可加性,因而可以更完整地衡量极端损失风险.

对VaR进行计算的多种统计方法中,极值理论作为度量极端市场条件下市场风险的一种方法,具有超越样本数据的估计能力,可以准确地描述分布尾部的分位数.极值理论有2类模型:分块样本极大值(BM)模型和超阈值(POT)模型.BM模型是应用极值理论计算VaR的一种便捷方法,但在计算过程中遇到一些困难:首先,如何分块无法清晰定义;其次,这是一种无条件方法,无法考虑其他解释变量的影响[1].为克服这些困难,文献[2-3]提出了POT方法,它聚焦于超出某个高阈值的数据和超出发生的时刻.如文献[2]提出了一个二维泊松过程同时考虑超出量和超出时刻,文献[4-5]运用该方法来研究风险管理中的VaR.考虑到实践中,通常可以找到一些影响收益的解释变量.而应用POT方法计算VaR的一个优势是它可以很容易把解释变量的影响考虑在内.相较于BM模型,POT模型能有效地使用有限的极端观测值,在实践中是最有用的模型之一.例如文献[6]最早把POT模型应用于股票市场收益并给出了很好的解释.文献[7-8]应用POT模型分别对沪深股市极端风险和地震风险进行了度量.文献[9-10]则分别研究了基于非齐次泊松过程的截断δ冲击模型和航空装备无故障工作期预计.但通过翻阅文献发现结合POT模型使用二维非齐次泊松过程拟合中国股票收益数据并计算风险度量的文献并不多见.

本文选取了中国非金融类跨国公司100强的民营企业中兴通讯股份有限公司从上市至2016年8月底的日收益数据,该数据具有明显的厚尾.首先,在选取阈值时,本文提出了一种综合考虑了模型估计的偏差和方差折中的差异度量方法,精确地估计出阈值的大小,以提高模型的拟合精度.然后,考虑到年度趋势和波动率等因素的影响,应用二维非齐次泊松过程拟合其损失的超出时刻和超出量,拟合结果显示使用非齐次泊松过程明显优于相应的齐次泊松过程,且估计系数可给出合理解释,说明解释变量起了显著作用.并通过模型校验说明所给模型的合理性.最后,给出拟合模型下的风险估计值供投资者参考以规避损失.

1 建模思路

1.1通过尾部差异度量选取阈值POT模型关注的是超过某一阈值的数据的利用.由于它可以充分地利用有限的极值数据,在实践中通常是非常有效的方法.以持有某只股票的多头头寸为例,记第t天观察到的该股票的负的日收益为rt,令η(ηgt;0)是一个事先指定的高阈值.假定第i次超出发生在第ti天,即rti≥η,则POT方法关注的是数据(ti,rti-η)的建模,此处rti-η表示的是超出阈值η的超出量.而对于股票的空头头寸,POT方法考虑的是满足正的日收益rti≥η的数据(ti,rti-η),其中η(ηgt;0)的选取与多头头寸类似.

对于给定的rt≥η,rti-η的条件分布函数记为Fη(x),由极值分布理论知:当选取的阈值足够大时,Fη(x)可以用广义帕累托分布(GPD)的分布函数来拟合[11],其形式如下:

其中ξ是形状参数,ψ(η)=α+ξ(η-β)gt;0是尺度参数.当ξ≥0时,x≥0;当ξlt;0时,0≤x≤-ψ(η)/ξ.

通过上述分析易见:利用POT模型对尾部分布进行估计时,首先需要选取合适的阈值η,使得Fη(x)≈G(x;ξ,ψ(η)).在实际中操作中,人们通常把Hill图法[12]和超额均值函数图法[13]结合起来使用,此方法虽然简单实用但是比较主观粗暴.考虑到选取太大的阈值,会导致超出数据太少,使得应用这些数据进行模型分析时的方差过大;反之,太小的阈值,虽然用于分析的数据多了,但是其对尾部的渐近性就会受到质疑,可能产生偏差较大的估计.基于统计学意义下的折中考虑,提出了下面的差异度量:

(1)

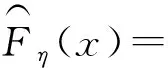
η*=arg minηD(η).

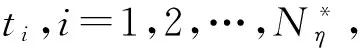
在实践中,发生时间ti为重要“稀有事件”(rti≥η*)发生的强度提供了有用的信息,一簇出现的ti意味着一段时间的大的市场下跌.超出量也是重要的,因为它提供了我们感兴趣的量.为此,结合极值理论,可以假定超出时刻和相伴损失{(ti,rti)}联合形成一个二维非齐次泊松过程,其强度测度具有下面的表示式:

A[(D1,D2)×(r,∞)]=

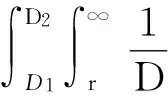
(2)

其中

(3)

是损失的密度函数,变量r≥η*,0≤D1≤D2≤T,参数αgt;0,β和ξ分别是尺度、位置和形状参数,当添加足标t时表示它们是时变的.

进一步假设xt=(x1t,…,xvt)T是先于时刻t获得的v个解释变量构成的向量,并假定式(2)中的3个参数ξt,αt和βt为解释变量的线性函数.具体而言,即假设

(4)

此处使用ln(αt)是为了满足对αt取正数的约束条件.从而,{(ti,rti)}的似然函数可以写为

(5)

其中

是密度函数式(3)对应的生存函数,变量z≥η*,记号[x]+=max(x,0).

注如果假定参数ξt、αt和βt在每一个交易日都是常数,则上述模型对应于二维齐次泊松过程的情形.

1.3检验模型的合理性校验一个对超出时刻和超出量构建的二维泊松过程是否合理,需要检验模型是否具有以下3个主要特性:验证超出率是适当的,检验超出量的分布以及模型的独立性假设.

超出率的检验:如果二维泊松过程模型适合,相邻两次超出的持续时间应该相互独立且服从同一个指数分布.具体而言,令t0=0,期待

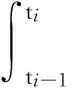
是独立同分布的标准指数变量.由于日收益是离散时间观测值,使用持续时间

通过观察Q-Q图并辅以KS和Box-Ljung检验来检查{zti}独立同分布于标准指数分布的有效性.

超出量的检验:在二维泊松过程模型下,超出阈值η*的量rti-η*服从形状参数ξt,尺度参数ψt(η*)=αt+ξt(η*-βt)的GPD.令

则应有{wti}独立同分布于标准指数分布[14].这样问题转化为对{wti}独立同分布于标准指数分布有

效性的检验,从而可以像检验{zti}那样处理.

模型的独立性检验:在去除解释变量的影响后,检验独立性假设的一个简单的方式是查看{zti}和{wti}的样本自相关函数(ACF)图.在独立性假设性下,期待{zti}和{wti}都无序列相关.在本文中使用Box-Ljung和x2检验对数据本身及数据之间的相互独立性进行检查.

1.4计算风险值VaR和ES对于给定的上尾概率p和阈值η*,由文献[15]知,rti-η*服从形状和尺度参数分别为ξt和ψt(η*)=αt+ξt(η*-βt)的GPD,因而VaR(p)可用下面的式子计算得到

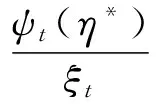
(6)

正如引言所述,与VaR相伴的ES是一个有用的风险度量,对于连续型损失,由ES的定义可得ES(p)=E[rt|rtgt;VaR(p)].再结合GPD的性质,得到下面的计算式

“猜成语”栏目自从开展以来好评如潮，每天短信爆棚，信和明信片也是让小意收到手软～我们将每期抽出3位答对的幸运意粉，送上神秘大礼一份！名单和答案将在隔期公布，小伙伴们快快参与起来吧～现在我们公布一下第23期的答案：爱屋及乌，望洋兴叹，日行千里，度日如年，拍案叫绝，百里挑一，晴天霹雳，昙花一现。

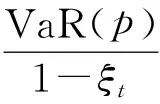
(7)

2 实证分析

2.1数据的描述性分析及阈值的选取众所周知,中国经济的快速发展使得中国资本市场极端不稳定.中国股票市场作为全球增速最快的资本市场,其中股票收益数据大都呈现出厚尾特征.为了研究股票收益的极值分布特性,从网易财经个股行情(http://quotes.money.163.com/trade/lsjysj-000063.html)下载了中兴通讯(ZTE)从1997年11月18日至2016年8月29日的日收盘价数据,以pt表示股票在第t个交易日的收盘价,利用对数收益公式rt=lnpt-lnpt-1计算得到4 549个ZTE日收益数据的观测值(单位:%),其中缺失值记为0.

下面是该数据的统计概述(表1)和时间序列图(图1).

表 1 ZTE日收益数据的统计概述

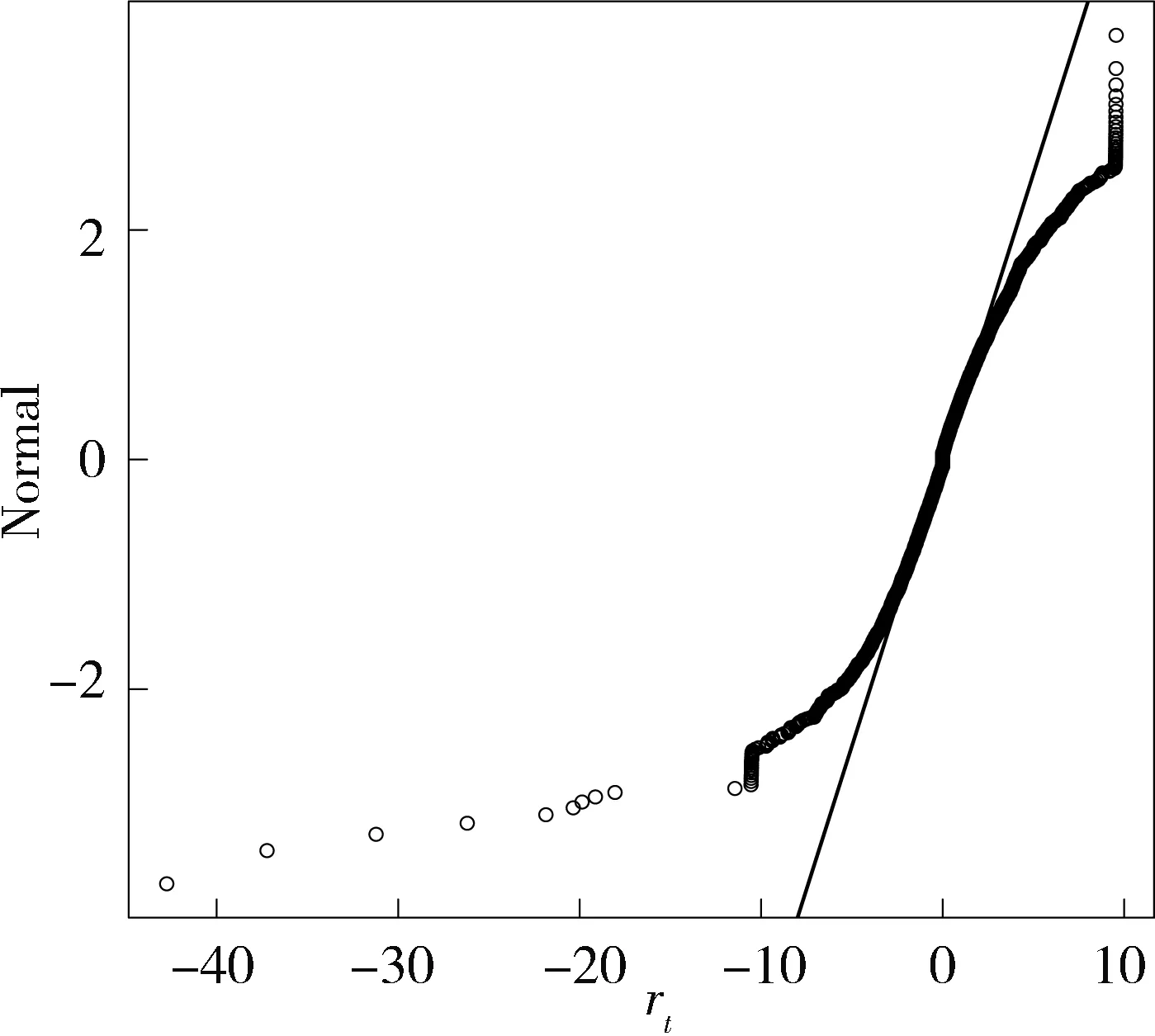
图 1 正态分布对ZTE日收益数据的Q-Q图

表1中偏度系数为负值隐含着该数据是不对称的,峰度系数值远大于3,提示该数据可能存在厚尾,JB统计量值的相伴p值几乎为0,暗示该数据不能用正态分布拟合.事实上,从时间序列图(本文略去)上也可观察到该数据有许多极端正的和负的收益,再通过图1,该数据相对正态分布的Q-Q图,可明显看出样本数据点并没有落在直线上,收益在上下两端均体现出厚尾的特征.综上,说明所研究的数据是非对称且具有较正态更厚的尾部.

本文仅考察持有ZTE的多头头寸的情形(空头情形类似),图2是根据(1)式计算出的差异度量D(η)随阈值变化的图形,由此获得最优阈值为η*=2.78,相应得到481个可用于建模的观测值.

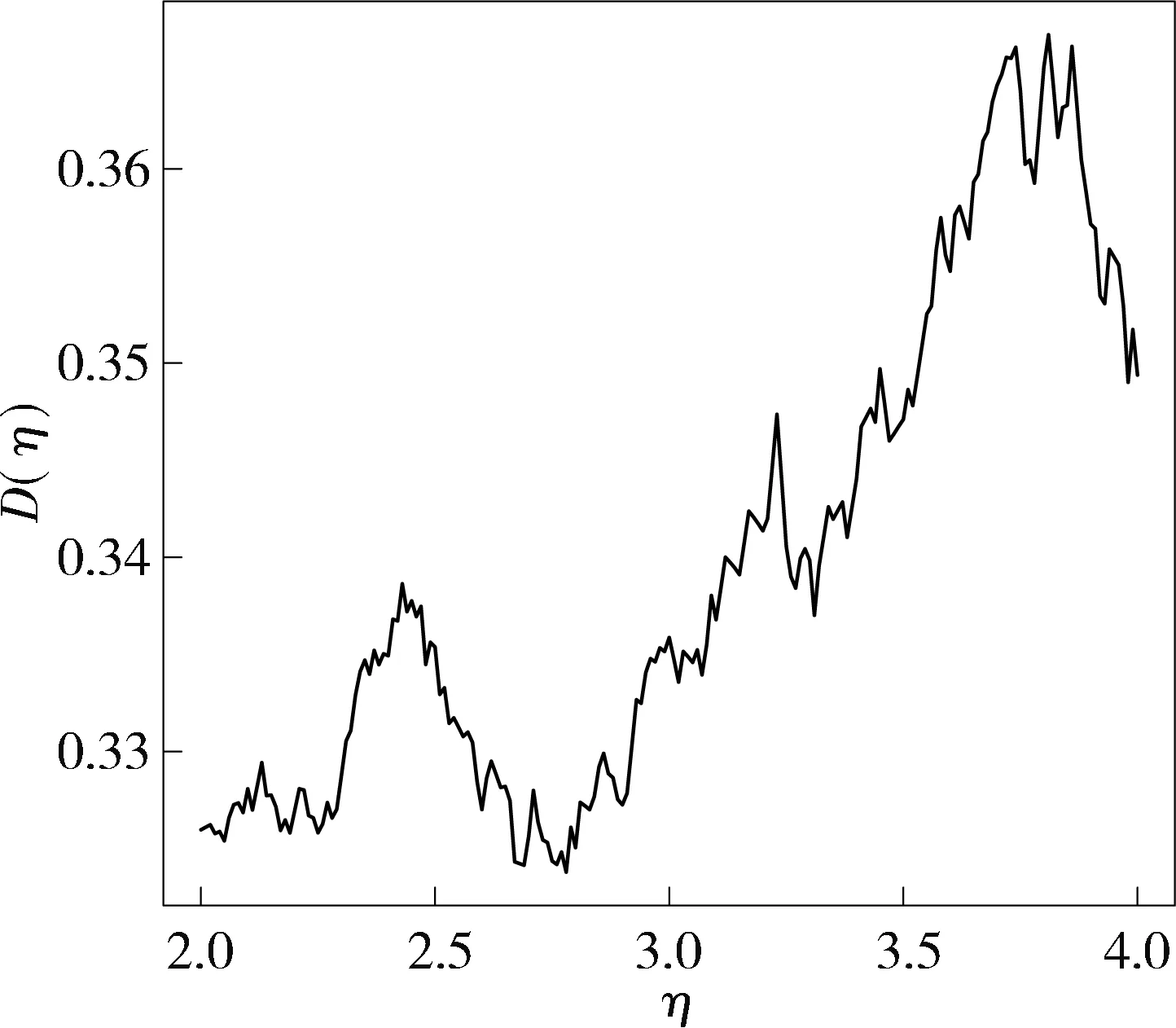
图 2 D(η)随η变化的关系图

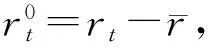
(8)

模型(8)的第一式中5个参数的标准误依次是0.052 9,0.043 1,0.095 6,0.013 9,0.020 7,且所有估计值在2×10-5的水平下是显著的.标准化残差的Ljung-Box统计量值Q(10)=14.164,相伴概率为0.165 6,说明在0.05的水平下残差是无自相关性的.又平方后的标准化残差的Ljung-Box统计量值Q(10)=1.266 1,相伴概率为0.999 5,说明该模型基本无arch效应.综上所述,用模型(8)来描述数据的条件异方差是足够的.

估计结果表明:形状参数ξt和尺度参数 ln(αt)显著依赖于年度趋势,且都是负的影响,说明随着时间的推移ZTE的极端负的日收益不仅数目在减少,波动率也在减小.但位置参数βt对年度趋势的依赖并不显著,说明它随时间推移发生的变化不明显;形状参数ξt没有受到波动率的量化度量的影响,但它受到ARMA(1,1)+GARCH(1,1)的波动率一些负的影响,这意味着ZTE的负的日收益对尾指的依赖也在减少;位置参数βt还受到另外两个解释变量的影响,且都是正的影响,隐含着它随着2种波动率的增大而显著增大.这些与实际情况是相一致的.

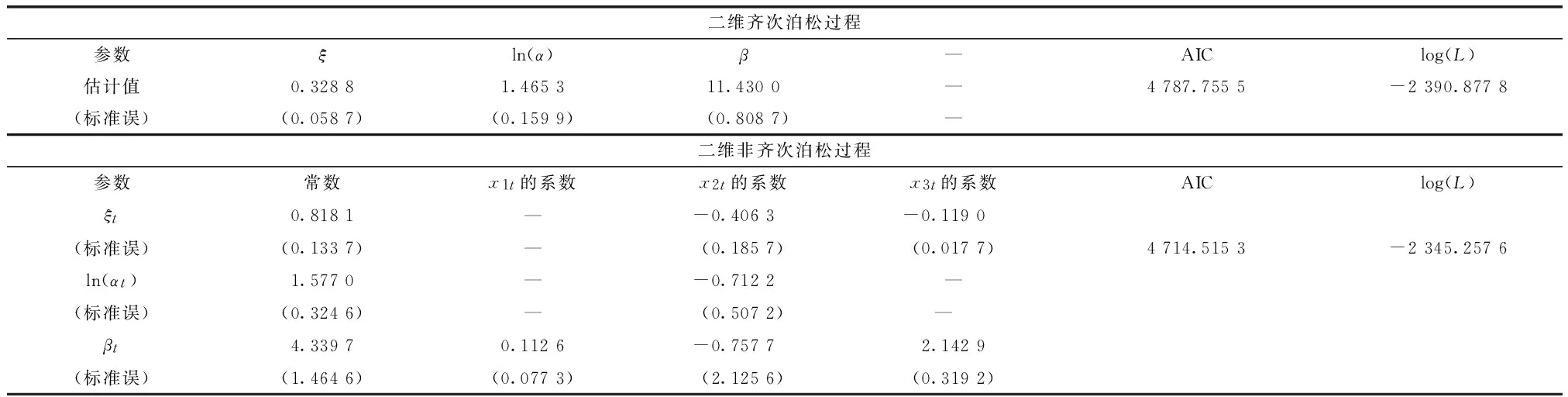
表 2 二维齐次和非齐次泊松过程拟合ZTE的日负收益的估计结果

注:表中“—”表示不存在此项.

2.3模型的合理性检验为说明模型的合理性,首先给出了取定阈值η*=2.78时,相邻2次超出的持续时间序列{zti}和超出量序列{wti}对标准指数分布的Q-Q图(图3).从图3可看出2个图中绝大多数数据点集中在参考线(数据与理论分布的第一和第三分位点确定的直线)附近,进一步对它们做右边ks检验,统计量D+的值分别为0.032 7和0.023 1,相伴p值分别为0.358 0和0.597 7,这些都说明{zti}和{wti}与标准指数分布比较接近.再对它们做Box-Ljung检验,滞后15阶x2统计量的值分别为24.024 2和14.720 9,对应的相伴p值分别为0.064 7和0.471 7,说明两序列本身都可以认为是相互独立的.图4是序列{zti}和{wti}的ACF图,注意到所有自相关函数基本落在渐近2倍标准差线内,说明它们都不存在序列相关.

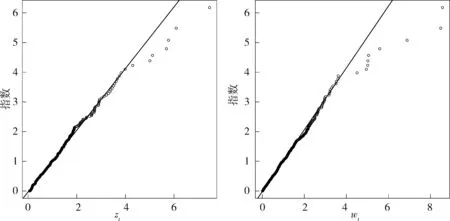
图 3 标准指数分布对相邻两次超出的持续时间(左)和超出量(右)的Q-Q图

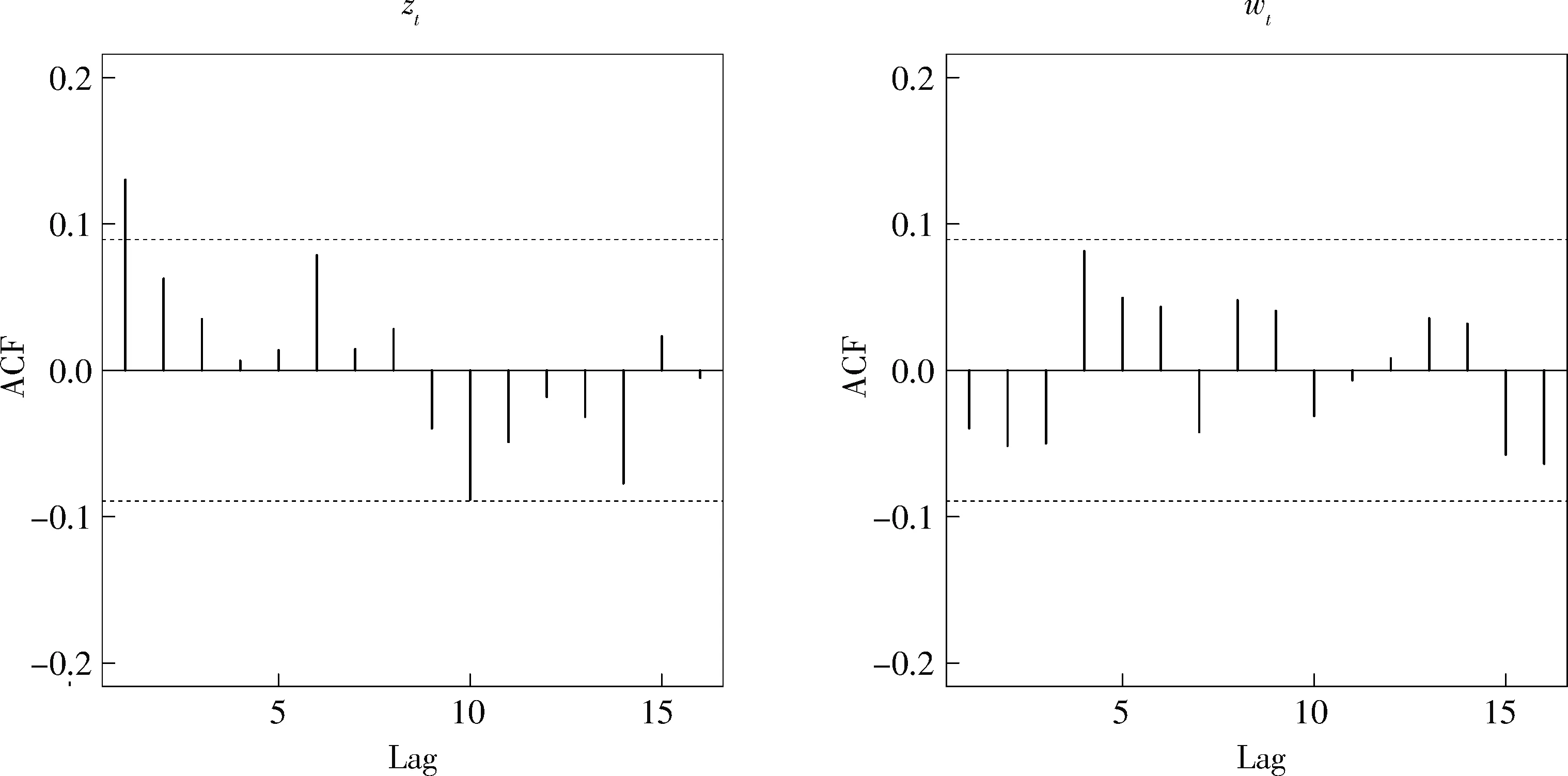
图 4 相邻2次超出的持续时间(左)和超出量(右)的ACF图

最后检验序列{zti}和{wti}之间的独立性,χ2检验统计量的值为230 880,相伴p值为0.239 6,可以认为两序列之间是没有关系的.

上述分析表明使用非齐次泊松过程拟合ZTE的日负收益是合理的.

2.4VaR和ES的计算接下来,关注持有1个单位人民币的一个多头头寸.不同于齐次泊松过程的情形,非齐次泊松过程使用解释变量的一大优势是参数可以适应市场条件的变化,利用(6)和(7)式分别计算出ZTE日收益的倒数第二天和最后一天的VaR和ES值,同时也给出使用齐次泊松过程得到的VaR和ES值方便对照比较(表3).

表 3 二维齐次和非齐次泊松过程拟合ZTE的日负收益的VaR和ES值

从表3可看出,不论哪种模型,对于给定的尾部概率,VaR值都明显小于相应的ES值,且同等条件下ES值增加的幅度更大,可见当实际中有极端损失发生时,ES可以弥补VaR低估风险这一不足之处,给出更稳健和保守的估计;随着尾部概率p的减小,VaR和ES值都在逐渐增大,但即使p=0.5%相应的风险值也是比较小的,这意味着异常损失的发生并不遥远,说明对股票收益进行风险控制是非常必要的;基于齐次泊松过程给出的风险值存在高估假象,而非齐次泊松过程不仅可以动态地捕捉VaR和ES等风险值,且由于用到了更多的数据信息给出的估计值更精准,容易达成有效防控风险的目的.

3 结束语

本文以具有极端日收益的中兴通讯股票数据为例,考虑到年度趋势和波动率等因素的影响,应用二维非齐次泊松过程拟合其损失超出时刻和相伴损失,给出模型的拟合和校验结果并得到了VaR和ES的估计值.研究结果表明非齐次泊松过程的拟合表现明显优于其特殊情形齐次泊松过程,说明引入解释变量是很有必要的.又有模型的校验结果显示相邻两次超出的持续时间序列和超出量序列满足模型成立的3个主要特征,因而本文所给拟合模型是合理的.另外,基于二维非齐次泊松过程不仅可以得到动态的风险估计值,且由于用到了更多的数据信息使得估计值较基于齐次泊松过程给出的更准确,从而为投资者控制风险提供更有效的数值参考,达到防范风险和及时止损的目的.

为计算简便,本文只给出3个解释变量的数值结果,投资者也可根据具体情况添加或修改解释变量.另外,本文所用的方法也可以为其他具有极端收益的股票数据的风险管理与分析提供借鉴与参考.

[1] COLES S. An Introduction to Statistical Modeling of Extreme Values[M]. New York:Springer-Verlag,2001.

[2] SMITH R L. Extreme value analysis of environmental time series:an application to trend detection in ground-level ozone[J]. Stat Sci,1989,4(4):367-393.

[3] DAVISON A C, SMITH R L. Models for exceedances over high thresholds[J]. J Roy Stat Soc,1990,B52(3):393-442.

[4] RUEY S T. Extreme value analysis of financial data[D]. Chicago:University of Chicago,1999.

[5] 陈守东,孔繁利,胡铮洋. 基于极值分布理论的VaR与ES度量[J]. 数量经济技术经济研究,2007,24(3):118-124.

[6] LONGIN F M. The asymptotic distribution of extremestock market returns[J]. J Business,1996,69(3):383-408.

[7] 张宗益,花拥军. 基于峰度法的POT模型对沪深股市极端风险的度量[J]. 系统工程理论与实践,2010,30(5):786-796.

[8] 郝军章,崔玉杰. 基于POT模型的巨灾风险度量与保险模式研究:以地震风险为例[J]. 数理统计与管理,2016,35(1):132-141.

[9] 张攀,马明,郑莹. 非齐次泊松过程下的截断δ-冲击模型[J]. 数学杂志,2016,36(1):214-222.

[10] 杨科,许连虎. 基于非齐次泊松过程的航空装备ffop预计[J]. 火力与指挥控制,2015,40(9):72-76.

[11] EMBRECHTS P, KJÜPPELBERG C, MIKOSCH T. Modelling Extremal Events for Insurance and Finance[M]. Berlin:Springer-Verlag,1997.

[12] HILL B M. Asimple general approach to inference about the tail of a distribution[J]. Ann Stat,1975,3(5):1163-1174.

[13] BENKTANDER G, SEGERDAHL C. On the analytical representation of claim distributions with special reference to excess of loss reinsurance[C]//16th International Congress of Actuaries,Brussels,1960.

[14] SMITH R L. Measuring risk with extreme value theory[D]. Chapel Hill:University of North Carolina,1999.

[15] RUEY S T. Analysis of Financial Time Series[M]. Hoboken:John Wiley Sons,2010.

(编辑 陶志宁)

Research for Risk Measures Based on Two Dimensional Inhomogeneous Poisson Process——a Case Study of ZTE Return Data

YU Jian1, XU Meiping2

(1.SchoolofScience,BeijingUniversityofCivilEngineeringandArchitecture,Beijing102616;2.SchoolofScience,BeijingTechnologyandBusinessUniversity,Beijing100048)

Considering some influence factors, such as anannual trend and volatilities, we employ two-dimensional inhomogeneous poisson process to fit exceeding times and associated returns of ZTE daily log return with heavy tails. Fitting results show that the inhomogeneous poisson process has better performance than corresponding homogeneous poisson process, which implies that these factors work well. The reasonableness of fitting model is clarified by model checking. Value at risk and associated expected shortfall are calculated from the fitting model. This research indicates that applying inhomogeneous poisson model can fully capture information from extreme values and get the more accurate estimates for risk measures, which could provide a reference for investors to avoid loss.

peak over threshold model; two dimensional inhomogeneous poisson process; value at risk; expected shortfall

F830.91

A

1001-8395(2017)06-0753-07

10.3969/j.issn.1001-8395.2017.06.008

2016-09-04

国家自然科学基金(11501017)

*通信作者简介:徐美萍(1971—),女,副教授,主要从事统计推断方面的研究,E-mail：xumiping2006@163.com