二面角求解的七种方法
河北 陈宝友
二面角求解的七种方法
河北 陈宝友
立体几何中的二面角是一个非常重要的数学概念,求二面角的大小更是历年高考命题的热点,在每年全国各省市的高考试题的大题中几乎都出现. 而这类问题又是很多学生感到困惑的,表现为求解困难,失分较为严重.究其原因有二:一是不能正确地作出二面角的平面角;二是在求二面角的平面角时存在计算障碍.常见基本题型包括:(1)求二面角的大小;(2)已知二面角的大小,求其它量;(3)求二面角的取值范围.其实求二面角的方法很多,本文讨论七种二面角的求解方法.
一、定义法求二面角
我们知道,从一条直线出发的两个半平面所组成的图形叫做二面角, 这条直线叫做二面角的棱, 这两个半平面叫做二面角的面,在棱上取点,分别在两面内引两条射线与棱垂直,这两条垂线所成的角的大小就是二面角的平面角.
本定义实际上为解题提供了添辅助线的一种规律,通过添加必要的辅助线,形成该二面角的一个平面角,再在该平面角内建立一个可解三角形,然后借助直角三角函数、正弦定理与余弦定理即可方便的解题. 定义法做二面角的平面角,要注意题设的特殊性,合理选择棱上的点,且过这点在两个平面内分别引棱的垂线,这两条射线所成的角,就是平面角.
【例1】如图,四棱柱ABCD-A1B1C1D1中,A1A⊥底面ABCD.四边形ABCD为梯形,AD∥BC,且AD=2BC.过A1,C,D三点的平面记为α,BB1与α的交点为Q.

(Ⅰ)证明:Q为BB1的中点;
(Ⅱ)若A1A=4,CD=2,梯形ABCD的面积为6,求平面α与底面ABCD所成二面角大小.
【解析】本题以直四棱柱为背景,考查考生的空间意识、运算和推演能力,考查空间整合思想的运用.
(Ⅰ)因为BQ∥AA1,BC∥AD,BC∩BQ=B,
AD∩AA1=A,
所以平面QBC∥平面A1AD,
从而平面A1QCD与这两个平面的交线相互平行,
即QC∥A1D.
故△QBC与△A1AD的对应边相互平行,
于是这两个三角形相似,

即Q为BB1的中点.
(Ⅱ)如图所示,在△ADC中,作AE⊥DC,垂足为E,连接A1E.

又DE⊥AA1,且AA1∩AE=A,
所以DE⊥平面AEA1,所以DE⊥A1E,
故∠AEA1为平面α与底面ABCD所成二面角的平面角.
因为BC∥AD,AD=2BC,
所以S△ADC=2S△BCA.
又因为梯形ABCD的面积为6,DC=2,
所以S△ADC=4,AE=4.


二、三垂线法求二面角
对于三垂线定理的内容我们非常清楚:在平面内的一条直线,如果和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直.通常当点P在一个半平面上则通常用三垂线定理法求二面角的大小,三垂线定理亦提供了另一种添辅助线的一般规律.
【例2】如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=AB,点E是PD的中点.

(Ⅰ)求证:PB∥平面AEC;
(Ⅱ)求二面角E-AC-B的大小.
【解析】本题考查三垂线定理及直线与平面平行的判定.
(Ⅰ)欲证PB∥平面AEC,根据直线与平面平行的判定定理可知,只需证PB与平面AEC内任一直线平行即可,
由PA⊥平面ABCD可得PA⊥AC,
又AB⊥AC,
所以AC⊥平面PAB,所以AC⊥PB.
连接BD交AC于点O,连接EO,
则EO是△PDB的中位线,
所以EO∥PB,所以PB∥平面AEC.

(Ⅱ)取AD的中点F,连接EF,FO,
则EF是△PAD的中位线,
所以EF∥PA,
又PA⊥平面ABCD,
所以EF⊥平面ABCD.
同理FO是△ADB的中位线,
所以FO∥AB,FO⊥AC,
由三垂线定理可知∠EOF是二面角E-AC-D的平面角.

所以∠EOF=45°,
而二面角E-AC-B与二面角E-AC-D互补,
故所求二面角E-AC-B的大小为135°.
三、棱的垂面法求二面角
所谓棱的垂面法,即空间一点作与棱垂直的平面,截二面角得两条射线,这两条射线所成的角就是二面角的平面角,其中面面垂直的性质定理和三垂线定理的应用是求解的关键.
【例3】如图所示,四棱柱ABCD-A1B1C1D1的所有棱长都相等,AC∩BD=O,A1C1∩B1D1=O1,四边形ACC1A1和四边形BDD1B1均为矩形.若∠CBA=60°,则二面角C1-OB1-D的余弦值为________.
【解析】如图,因为四边形ACC1A1为矩形,
所以CC1⊥AC.
同理DD1⊥BD.
因为CC1∥DD1,
所以CC1⊥BD.
而AC∩BD=O,
因此CC1⊥底面ABCD.
由题设知,O1O∥C1C.故O1O⊥底面ABCD.
过O1作O1H⊥OB1于H,连接HC1,
由O1O⊥底面ABCD,知O1O⊥底面A1B1C1D1,
于是O1O⊥A1C1.

又因为四棱柱ABCD-A1B1C1D1的所有棱长都相等,
所以四边形A1B1C1D1是菱形,
因此A1C1⊥B1D1,从而A1C1⊥平面BDD1B1,
所以A1C1⊥OB1,
于是OB1⊥平面O1HC1,进而OB1⊥C1H,
故∠C1HO1是二面角C1-OB1-D的平面角.
不妨设AB=2,
因为∠CBA=60°,

在Rt△OO1B1中,




四、射影面积法求二面角
斜面面积和射影面积的关系公式为S′=S·cosθ,其中S为原斜面面积,S′为射影面积,θ为斜面与射影所成二面角的平面角,这个公式对于斜面为三角形、任意多边形都成立.

【例4】如图,在正方体ABCD-A1BC1D1中,E为AA1的中点,则平面B1DE与底面ABCD所成的二面角的余弦值为________.
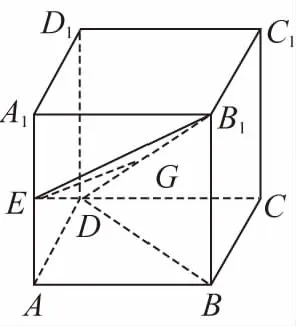
【解析】在正方体ABCD-A1BC1D1中,AA1⊥底面ABCD,所以A为点E在底面ABCD上的射影,
△ABD是△EB1D在底面ABCD上的射影三角形.

在△EB1D中,过E作EG⊥B1D于G,



设平面B1DE与底面ABCD所成的二面角为θ,

五、补棱法求二面角
补棱法是针对解构成二面角的两个半平面没有明确交线的求二面角题目,要将两平面的图形补充完整,使之有明确的交线,此即称为补棱,然后借助前述的定义法与三垂线法解题.
【例5】如图所示,四棱锥P-ABCD的底面ABCD是边长为1的菱形,∠BCD=60°,E是CD的中点,PA⊥底面ABCD,PA=2.
(Ⅰ)证明:平面PBE⊥平面PAB;
(Ⅱ)求平面PAD和平面PBE所成二面角(锐角)正弦值的大小.

【解析】本题的平面PAD和平面PBE没有明确的交线,依本法显然要补充完整(延长AD,BE相交于点F,连接PF),再在完整图形中找一个适合的点形成二面角的平面角解之.
(Ⅰ)证明:连接BD,因为ABCD是菱形,且∠BCD=60°,所以△BCD是等边三角形.
因为E是CD的中点,所以BE⊥CD,又AB∥CD,
所以BE⊥AB.
又因为PA⊥平面ABCD,
BE⊂平面ABCD,所以PA⊥BE.
而PA∩AB=A,因此BE⊥平面PAB.
又BE⊂平面PBE,所以平面PBE⊥平面PAB.
(Ⅱ)延长AD,BE相交于点F,连接PF.
过点A作AH⊥PB于H,
由(Ⅰ)知平面PBE⊥平面PAB,
所以AH⊥平面PBE.
在Rt△ABF中,因为∠BAF=60°,
所以AF=2AB=2=AP.
在等腰Rt△PAF中,取PF的中点G,
连接AG,则AG⊥PF.
连接HG,由三垂线定理的逆定理得,PF⊥HG.
所以∠AGH是平面PAD和平面PBE所成二面角的平面角(锐角).

在Rt△PAB中,


所以,在Rt△AHG中,

六、补形法求二面角
某些特殊几何体通过补形法,构造常见的长方体、正方体、正四面体等模型,使抽象问题简单化,易找到二面角的平面角.互相垂直的两两长(正)方形补成长(正)方体易求二面角和体积.


【解析】因为AB=BC=1,SD=1,故可把原四棱锥补成正方体ABCD-A1B1C1S,连接A1B,则面ASD与面BSC所成的二面角,即为面ADSA1与BCSA1所成的二面角.
因为A1S⊥SD,A1S⊥SC,所以∠CSD为所求二面角的平面角,∠CSD=45°,故所求二面角为45°.
七、向量法求二面角
向量法解立体几何是一种十分简捷且常见的解法,可以说所有的立体几何题都可以用向量法求解,用向量法解立体几何题时,通常要建立空间直角坐标系,写出各点的坐标,然后将几何图中的线段写成用坐标法表示的向量,进行向量计算解题.

【例7】如图,已知四棱锥P-ABCD中,PA⊥底面ABCD,且ABCD为正方形,PA=AB=a,点M是PC的中点.

(Ⅰ)求BP与DM所成的角的大小;
(Ⅱ)求二面角M—DA—C的大小.


设直线BP与DM所成的角为θ,


所以BP与DM所成的角的大小为90°.






所以所求的二面角M—DA—C的大小为45°.
利用向量法解决空间角的求解问题,首先需要根据几何体的结构特征建立合理的空间直角坐标系,准确求出点以及向量的坐标是解决此类问题的基础,准确求解直线的方向向量与平面的法向量是关键,最后只需利用这些向量表示所求角即可.解题时,要注意向量的夹角与所求角之间的关系,进行正确转化.如求解二面角时,要注意根据几何体的结构特征准确判断二面角的取值范围;求解线面角时,要注意三角函数名称的变化.

河北省衡水市郑口中学)

