探讨增元法求解最值问题

陕西 王仕林

探讨增元法求解最值问题

陕西 王仕林

求最值问题是高中数学中最重要的问题，也是高考考查的热点之一；它渗透在高中数学各个模块中；求最值的方法也多种多样，增元法就是其中一种最重要的方法；通常把要求的最值代数式通过增元化成函数，然后利用函数求最值的方法，达到求最值的目的.本人归纳出利用增元的方法求函数最值问题的三种模型，相对于常规方法而言，这种方法可以起到事半功倍的效果.

方法2：以上证明运用了函数求最值的方法，下面用本文所讲的增元法来解决.

【评注】以上两种不同的求解方法都利用了均值不等式求最值，但明显第一种方法转化成均值不等式形式的过程中，利用了通分、相除、凑项、拆项、换元等五步整理，而第二种方法只经过了增元、把1代换、相乘等三步就完成了，而且运算过程比较简单.

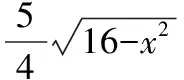
【解析】方法1：该题是无理函数求最值问题，用代数法就必须去掉根号，可考虑三角换元法.

设x=4cosα(0≤α≤π) ，则

又0≤α≤π，所以-φ≤α-φ≤π-φ，

所以-sinφ≤sin(α-φ)≤1，

所以-12≤13sin(α-φ)≤13，

即f(x)max=13,f(x)min=-12.

方法2：利用增元法，效率大大增强.

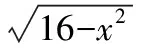
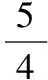
【评注】从以上两种证明方法可以看出，三角换元法的运算比较繁琐，而增元法最后转化成数形结合，运算少，而且很直观.

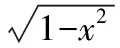
【解析】方法1：本题初看不知从哪下手，仔细分析后可考虑用三角换元法.

方法2：由于该函数比较复杂，特别是含有根号，因此，可考虑用增元法求解.

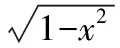
【评注】以上两种方法求解，虽然最后都用了斜率的几何意义来求其最大与最小值问题，但是第一种方法太麻烦了，用了两次换元才知动点P的轨迹，尤其是P(cosθ，sinθ)(0≤θ≤π)很不容易找到.而利用增元法，原函数就变成了条件等式下的二元函数求最值问题，而且很容易想到用斜率的几何意义来求解.

陕西省汉中市西乡二中)