亏数为 1 的幂等变换生成半群的R*-关系
叶硕海,杨秀良
(杭州师范大学理学院,浙江 杭州 310036)
亏数为 1 的幂等变换生成半群的R*-关系
叶硕海,杨秀良
(杭州师范大学理学院,浙江 杭州 310036)
令Singn为 [n]={1,2,…,n} 上的奇异变换半群.En-1为Singn中亏数为 1 的幂等变换的集合,对En-1的任意非空子集I, 本文刻画其生成子半群S(I) 满足关系式
(α,β)∈R*⟺Ker(α)=Ker(β),∀α,β∈S(I)
的特征.
亏数为 1 的幂等元; 简单有向图; 变换的核; R*-关系
0 引 言
对半群理论可参考文[1]. 设Singn为 [n] 上的奇异变换半群, 对任意的α∈Singn,α的亏数定义为 def(α)=n-|im(α)|. 并且记En-1为Singn中所有亏数为 1 的幂等变换的集合, 它中任意一个元具有形式χ(a,b)(a,b∈[n],a≠b), 其中 (a)χ(a,b)=b,(t)χ(a,b)=t,∀t≠a. 设I为En-1的任一个非空子集, 令半群S(I)=I. 在文[2]中, Howie特征了S(I)=Singn. 此外,文 [3]证明了奇异保序变换半群On可由生成, 且为H- 平凡的正则半群. 文[4]证明了奇异递减变换半群可由 {χ(i,j)|jlt;i,i,j∈[n]} 生成, 且为H-平凡的富足半群. 文[5]综合[3-4], 进一步给出了S(I)为H-平凡的特征. 纵观文[2-3], 文[6]中给出了S(I) 为正则半群的充要条件. 进一步我们可探讨S(I) 为富足半群的充要条件.
本文中将刻画半群S(I)满足
(α,β)∈R*⟺Ker(α)=Ker(β),∀α,β
的特征,这里Ker(α)={(x,y)∈[n]×[n] | (x)α=(y)α}.
1 定理陈述
设I为En-1中的一个非空子集, 构造一个简单有向图D(I), 其顶点集为 [n], 其有向边集为E(D(I))={(b,a)∈[n]×[n] |χ(a,b)∈I}, 并称D(I) 为I的伴随有向图. 反之, 若有向图D以V(D)=[n] 为顶点集, 以E(D)⊆[n]×[n]-{(a,a) |a∈[n]} 为有向边集, 可构造En-1的一非空子集I(D)={χ(a,b)| (b,a)∈E(D)}, 并用S(D) 来表示由I(D) 生成的半群 (见文[2],[5-7]).
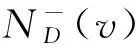
x1→x2→…→xn, ∀1≤j≤m-1, (xj,xj+1)∈E(D)
的子图称之为有向路径, 简称路径.
设S为任意一个半群,a,b∈S,S上的R*-关系定义为 (a,b)∈R*当且仅当a,b在一个包含S的半群中关于Green-关系R等价(见文[4],[8]).
定理1设I为En-1中的非空子集, 则下面条件等价
1) 在半群S(I) 中下面关系成立
(α,β)∈R*⟺Ker(α)=Ker(β),∀α,β∈S(I);
2) 在I的伴随图D(I) 中, 若存在以下D′ 的子图
→z→xm→…→x2→x1=x,
→z→ym′→…→y2→y1=y,
其中m,m′≥1 且 {x1,x2,…,xm}∩{y1,y2,…,ym′}=∅ 并且
∉{z,x1,x2,…,xm,y1,y2,…,ym′}.
则在D(I) 中必存在子图
x→…→y
或
y→…→x
或
x→…→u←…←y,
其中u∈[n].
2 几个预备引理
为方便起见, 在此始终认为D为一个以 [n] 为顶点集的有向图.
引理1设I为En-1的非空子集,x,y∈V(D(I)),x≠y, 则在S(I) 中存在元素ω满足 (x)ω=y的充要条件为在D(I) 中存在从y到x的有向路径.
证明见文[7] 引理3.4.
■
引理2设I为En-1的非空子集,x,y∈V(D(I)),x≠y. 若在D(I) 中存在路径
P:y=am→am-1→…→al→a0=x,
其中am,am-1,…,a1,a0两两不同, 则在S(I)1中存在元素ξ,η满足
以及
ξ=1V(D(I)),η=χ(x,y).
情况2否则取

以及
引理3设I为En-1中的非空子集,x,y∈V(D(I)),x≠y. 若在D(I) 中存在q∈[n]-{x,y}, 满足
Q1:x=td→td-1→…→t1→t0=q,
Q2:y=se→se-1→…→s1→s0=q,
为D(I) 中交点仅为q的有向路径, 且t0,t1,…,td两两不同,s0,s1,…,se两两不同, 则在S(I)1中存在元素ω,ζ满足
以及
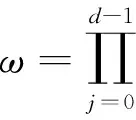
χ(tj,tj+1).
引理4设S为任意一个半群,a,b∈S, 则下面条件等价:
1) (a,b)∈ R*;
2) 对任意的x,y∈S1,xa=ya⟺xb=yb.
证明见文[4] 引理 2.4.
■
3 定理 1 中 (1)⟹(2) 的部分
证明反证法, 假设在D(I) 中存在形如定理1中D′ 的子图, 其中m,m′≥1 且 {x1,x2,…,xm}∩{y1,y2,…,ym′}=∅ 并且
∉{z,x1,x2,…,xm,y1,y2,…,ym′},
但形如下面的子图都不存在:x→…→y及y→…→x以及x→…→u←…←y, 其中,u∈[n].
下面来说明在S(I) 中, 存在元素α,β∈S(I) 满足
Ker(α)≠Ker(β),
但有
(α,β)∈R*.
为此现定义
σ1=χ(x2,x3)。…。χ(xm-1,xm)。χ(xm,z),
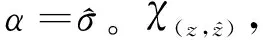
假如x2,…,xm不存在, 则取σ1=χ(x,z),σ2做类似处理.
由计算马上有
以及
其中Λ={x1,…,xm,y1,…,ym′,z,},v1,v2,…∈[n]-(Λ∪{x,y}). 并且由于容易得对任意的δ,λ∈S(I), 由。α=。α可得出。β=。β.
显然又有 Ker(α)≠Ker(β).
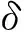
因此, 存在u∈[n] 使得
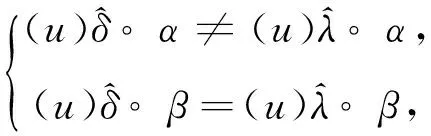
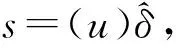
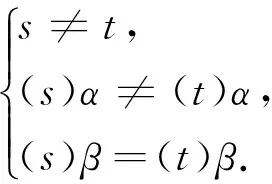
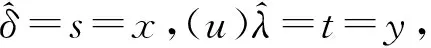
x→…→y=u
或是
y→…→x=u
或是
x→…→u←…←y,
这便与假设矛盾.
■
4 定理 1 中 (2)⟹(1) 的部分
证明若 (α,β)∈S(I) 且 Ker(α)=Ker(β), 则显然有 (α,β)∈RSingn, 从而有 (α,β)∈R*.
现假设 (α,β)∈R*且 (x)α=(y)α=z, (x≠y), 下面我们来说明 (x)β=(y)β, 即说明 (x,y)∈Ker(β).
情况1若在D(I) 中存在
y=am→am-1→…→a1→a0=x.
不妨设a0,a1,…,am两两不相等, 则由引理 2 知在S(I)1中存在ξ,η满足
以及
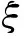
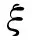
进而有
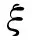
因此有 (x,y)∈Ker(β).
在情况1不成立的情况下, 由 (x)α=(y)α=z以及引理1 知存在D(I) 中从z到x的路径P1, 以及从z到y的路径P2, 此处不妨设P1中顶点互不相同,P2也如此, 容易知存在z′ 为P1,P2中的一个公共顶点满足:
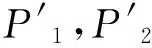
情况2若z≠z′, 此处有两种子情况.
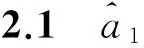
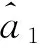
U1:x=td→td-1→…→t1→t0=u,
U2:y=se→se-1→…→s1→s0=u.
此处不妨设u为U1,U2唯一的公共顶点且t0,…td互不相同,s0,…,se互不相同, 从而由引理 3 知存在ω,ζ∈S(I)1满足:
以及
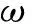
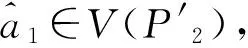
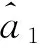
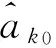
y.
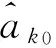
从而由条件 (2) 以及假定情况 1 不成立知,在D(I) 存在顶点u使得D(I) 中有形如下面的子图
x→…→u←…←y,
因此类似于情况 2.1 我们又知 (x,y)∈Ker(β).
情况3若z=且id(z)=0, 即在D(I) 中没有形如 (g,z) 的有向边, 则有 (z)α=z, 从而(x)α=(y)α=(z)α=z.由 (z,x)∈Ker(α) 以及情况 1 知 (x,z)∈Ker(β),
同理又有 (y,z)∈Ker(β). 因此有 (x,y)∈Ker(β).
情况4z=z′ 且 存在∉V(P2)∪V(P1) 使得 (,z)∈E(D(I)), 类似于情况 2,可说明 (x,y)∈Ker(β).
情况5z=z′ 且在 {a1,a2,…,at-1} 中存在ap0使得 (ap0,z)∈E(D(I)), 现取
Q1:ap0→…→a1→a0=x,
Q2:ap0→z→br→…→b1→b0=y.
则ap0必为Q1,Q2唯一的公共顶点, 且ap0+1∉V(Q1)∪V(Q2). 因而类似于情况 2, 我们又可说明 (x,y)∈Ker(β).
情况6若z=z′ 且 (at,z)∈E(D(I)), 此时若存在v∈V(P1)∪V(P2) 满足 (v,at)或 (v,z)∈E(D(I)), 则类似于情况 2, 也可证明 (x,y)∈Ker(β).
若存在aq0∈{a1,a2,…,at-2} 使得 (aq0,at)∈E(D(I)), 则类似于情况5可知 (x,y)∈Ker(β).
若存在bj0∈{b1,b2,…,br} 使得 (bj0,at)∈E(D(I)), 则在D(I) 中便有如下子图:
bj0+1→bj0→at→…→a1→a0=x,
bj0+1→bj0→bj0-1→…→b1→b0=y,
其中 {at,at-1,…,a1,a0}∩{bj0-1,…,b1,b0}=∅ 且bj0+1∉{at,at-1,…,a1,a0,bj0,bj0-1,…,b1,b0}, 这里若j0=r, 则取bj0+1=z. 类似于情况2, 可证明 (x,y)∈Ker(β).
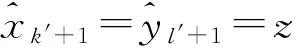

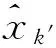
并且设在D(I) 中,Ω中的顶点满足下面的各条件:
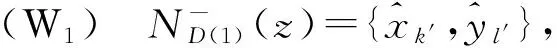
(W2) 在D(I) 中不存在从yi到xj的路径, 1≤j≤k, 1≤i≤l.
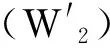
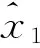
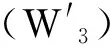
显然, 若Ω中的点不满足 (W1) ,则可把情形归至情况 2.
若Ω不满足 (W2), 则在D(I) 中存在路径
S:yi0=c1→c2→…→ce=xj0,e≥1,
此处不妨设c1,c2,…,ce两两不同 且都不在 {y1,y2,…,yl} 中, 则下面定义的两条路径
R:yi0=c1→c2→…→ce=xj0→…→x1=x,
R′:yi0→…→y2→y1=y,
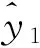
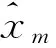
y.
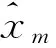
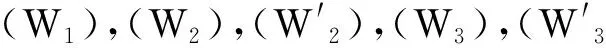
现在在V(Ω) 上定义一个全序,
x=x1x2…xk…z…yl…y1=y.
由引理 1 不难证明对任意的π∈S(I) 有
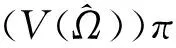
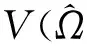
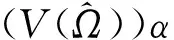
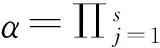
χ(pj,qj), ∀1≤t≤s.
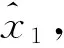
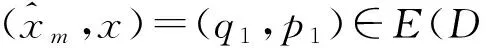
进而取
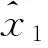
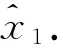
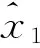
现设 (x)αt∈V(Ω) , 往证 (x)αt⪯(z)αt. 下面分4种子情况来讨论.
情况6.1若 (x)αt-1∉V(Ω). 现设x′=(x)αt-1, 而由 (x′)χ(pt,qt)∈V(Ω) 知
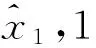
这是由于首先由 (W2) 知 (x)αt≠yi, ∀1≤i≤l. 假如
m≥2,
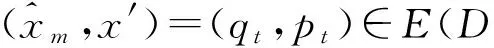
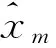
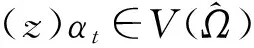
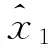
情况6.2若 (x)αt-1∈{x1,…,xk}, 类似于情况6.1知
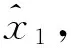
因而又有
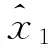
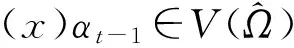
(x)αt-1⪯(z)αt-1,
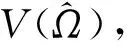
(x)αt=(x)αt-1⪯(z)αt-1=(z)α.
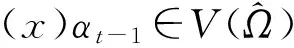

(x)αt⪯(x)αt-1。χ(pt,qt)⪯(z)αt-1。χ(pt,qt)=(z)αt.
因此, 由归纳原理知若有 (x)αt∈V(Ω), 则有 (x)αt⪯(z)αt. 特别地, 由于 (x)α=(x)αs=z∈V(Ω), 从而我们有z=(x)α⪯(z)α.
类似的, 可证z=(y)α(z)α. 因此便有 (x)α=(y)α=(z)α=z. 因而由情况1以及 (x,z)∈Ker(α), (y,z)∈Ker(α), (α,β)∈R*知
(x,z)∈Ker(β), (y,z)∈Ker(β),
因此有 (x,y)∈Ker(β).
从而有 Ker(α)⊆Ker(β). 同理可证相反的包含关系. 因此有 Ker(α)=Ker(β).
[1] HOWIE J M. An introduction to semigroup theory[M]. London: Academic Press, 1976: 1-13.
[2] HOWIE J M. Idempotent generators in finite full transformation semigroups[J]. Proceedings of the Royal Society of Edinburgh, 1977, 81(81):317-323.
[3] HIGGINS P M. Idempotent depth in semigroups of order-preserving mappings[J]. Proceedings of the Royal Society of Edinburgh, 1993, 124(5):1045-1058.
[4] UMAR A. On the semigroups of order-decreasing finite full transformations[J]. Proceedings of the Royal Society of Edinburgh, 1991, 120(1):129-142.
[5] YANG X, YANG H.H-trivial transformation semibands and digraphs[J]. Communications in Algebra, 2005, 33(5):1461-1481.
[6] YANG X, YANG H. Maximal regular subsemibands ofSingn[J]. Semigroup Forum, 2006, 72(72):75-93.
[7] YANG X, YANG H. Isomorphisms of transformation semigroups associated with simple di- graphs[J]. Asian-European Journal of Mathematics, 2009, 2(4):727-737.
[8] FOUNTAIN J. Abundant semigroups[J]. Proceedings of the London Mathematical Society, 1982, 44:103-129.
(α,β)∈R*⟺ Ker(α)=Ker(β), ∀α,β∈S(I).
TheR*-relationontheSemigroupsGeneratedbyIdempotentsofDefect1
YE Shuohai, YANG Xiuliang
(School of Science, Hangzhou Normal University, Hangzhou 310036,China)
LetSingnbe the semigroup of all the singular transformations on [n]={1,2,…,n}. LetEn-1be set of all the idempotents of defect 1 inSingn. For any non-empty subsetIofEn-1, we characterized the necessary and sufficient condition forIsuch that the following relation holds:
idempotent of defect 1; simple digraph; kernel of a transformation; R*-relation
2017-02-10
杨秀良(1963—),男,教授,主要从事半群代数研究.E-mail: yxl@hznu.edu.cn
10.3969/j.issn.1674-232X.2017.05.015
O152.7MSC201043A22
A
1674-232X(2017)05-0531-08

