概率统计中与分布列有关的问题的探讨

广西 包日勇

概率统计中与分布列有关的问题的探讨

广西 包日勇

新课标高考中概率统计的大题往往都是概率与统计的结合，既含有统计方面的知识，也有概率的计算，理科中更注重分布列的研究，而超几何分布和二项分布是最为常考的两种概率分布.如何根据已知条件，快速确定概率分布的类型，熟练掌握这两种概率分布的解题要点，是决胜高考的关键.

一、抓住关键字眼，准确把握分布类型

概率统计的大题往往文字较多，篇幅较长，在解题过程中，要学会抓住关键字眼，快速准确地判断出概率和分布列的类型，切忌生搬硬套.

【例1】为了降低汽车尾气的排放量，某厂生产甲、乙两种不同型号的节排器，分别从甲、乙两种节排器中随机抽取100件进行性能质量评估检测，综合得分情况的频率分布直方图如图所示：

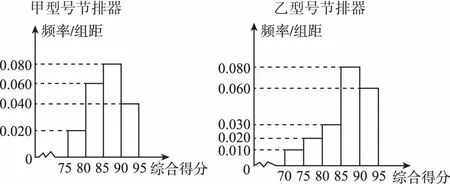
节排器等级及利润如表格

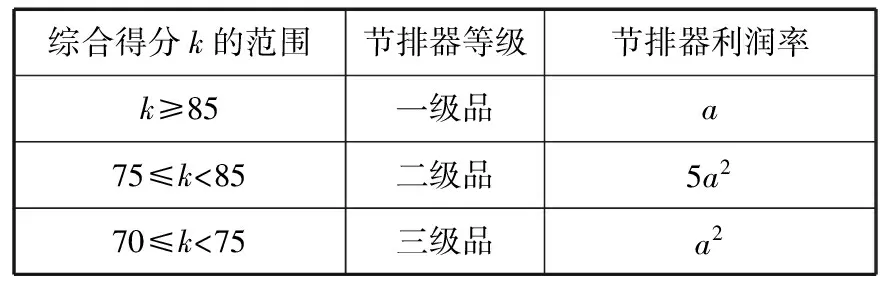
综合得分k的范围节排器等级节排器利润率k≥85一级品a75≤klt;85二级品5a270≤klt;75三级品a2

(Ⅰ)将频率分布图中的频率视为概率，则

(ⅰ)若从甲型号节排器中按节排器等级用分层抽样的方法抽取10件，再从这10件节排器中随机抽取3件，求至少有2件一级品的概率；

(ⅱ)若从乙型号节排器中随机抽取3件，求二级品数ξ的分布列及数学期望E(ξ)；

(ⅲ)从抽出的乙型号节排器中随机抽取3件，求二级品数η的分布列及数学期望E(η)；

(Ⅱ)从长期来看，投资哪种型号的节排器平均利润较大？

分析：第(ⅱ)问中从乙型号节排器中随机抽取3件，求二级品数ξ的分布列，因为题目中有“将频率分布图中的频率视为概率”，说明可认为乙型号节排器有无数多个，为对无限总体的研究，可以看作做了3次独立重复试验，研究取得二级品这一事件发生的次数问题，符合二项分布.第(ⅲ)问中从抽出的100件乙型号节排器中随机抽取3件，即“在(从)……(有限个中)选取……”，则为对样本的研究，为有限总体不放回抽样，研究二级品数这一事件发生的问题，则考的是古典概型，也就是相当于100个产品中含有25个二级品，从中抽出3个，研究其中所含的二级品数问题，符合超几何分布.

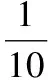
(ⅱ)若从乙型号节排器中随机抽取3件，从生产线上下来的乙型号节排器有无数多个，可以看作一个独立重复过程，把取得二级品这一事件看作A，相当于做了3次独立重复试验，研究事件A发生的次数问题，为二项分布.

所以ξ～B(3,0.25)，E(ξ)=3×0.25=0.75.

(ⅲ)从抽出的100件乙型号节排器中随机抽取3件，属于有限总体不放回抽样，研究其中所含的二级品数问题，为超几何分布.

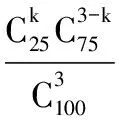
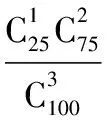
(Ⅱ)设X为投资甲型号节排器获得的平均利润，Y为投资乙型号节排器获得的平均利润，由题意得出甲、乙的分布列如下：

Xa5a2P0．60．4

甲：E(X)=0.6a+2a2

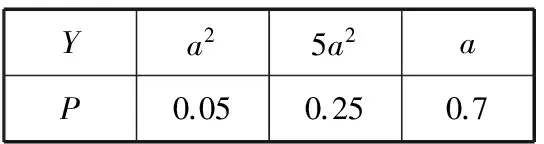
Ya25a2aP0．050．250．7

乙：E(Y)=0.7a+1.3a2

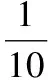
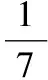
评析：本题在解题过程中，认真弄清题意，确定类型，区分这两种概率计算，分析所研究的分布列满足的条件，才能顺利求解.

解题要点一：与统计相结合的概率题目，通常以抽样与频率分布直方图相结合为背景，若有“频率视为概率”的字眼，则为对无限总体的研究，有 “实验具有重复性”，“有放回抽样”等字眼，则整个过程为一重复过程；有“实验次数多”字眼，虽然对总体抽样时不放回，但在大量的情况下可看作独立重复，则考的是独立重复试验，若研究某一事件有多少次发生问题，一般为二项分布.

解题要点二：若有“在(从)……(有限个中)选取……”的字眼，则为对样本的研究，为有限总体，若采用不放回抽样，是古典概型，若研究恰好有某一事件发生的问题，则考的是古典概型，通常为超几何分布.

二、审清题意，分析清楚概率事件

在解题过程中，除了要抓关键字眼外，还要注意分析要研究的概率事件，正确判断随机变量的取值.有些题目虽然表面上看满足超几何分布或二项分布的前提，但所研究的概率事件却并不相同.

【例2】(2015·福建)某银行规定，一张银行卡若在一天内出现3次密码尝试错误，该银行卡将被锁定，小王到银行取钱时，发现自己忘记了银行卡的密码，但是可以确定该银行卡的正确密码是他常用的6个密码之一，小王决定从中不重复地随机选择1个进行尝试.若密码正确，则结束尝试；否则继续尝试，直至该银行卡被锁定.

(Ⅰ)求当天小王的该银行卡被锁定的概率；

(Ⅱ)设当天小王用该银行卡尝试密码次数为X，求X的分布列和数学期望.

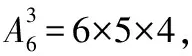
解：(Ⅰ)设“当天小王的该银行卡被锁定”的事件为A，则

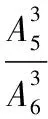
(Ⅱ)依题意得，X所有可能的取值是1，2，3，

所以X的分布列为

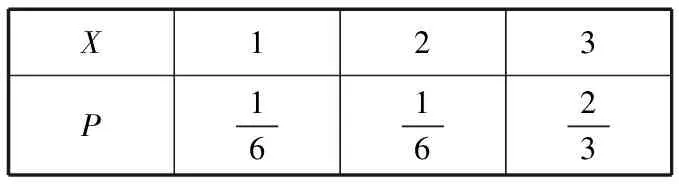
X123P161623

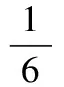
评析：题目中属于有限总体，不放回的抽样，但研究的是尝试密码次数，这与超几何分布研究的概率事件不同.因此在解题中既要注意分析前提条件，也要看清概率事件才行.

解题要点三：在概率统计解题中，仔细审题，注意分析要研究的概率事件，正确判断随机变量的取值，超几何分布和二项分布有着不同的前提，超几何分布是针对有限总体不放回，二项分布是针对有放回或无限总体情形.但也不能只看到这一前提就判断出分布列的类型，要清楚“从含有M件次品的N件产品中任取n件，其中所含次品数问题”，才服从超几何分布；而“在n次独立重复试验中，事件A发生的次数问题”才服从二项分布.若“从含有M件次品的N件产品中任取n件”，但研究的不是次品数问题，则也不是超几何分布.同样若“在n次独立重复试验中”，但不是研究某事件发生的次数，则也不是二项分布.因此解题中还应注意题目中要研究的概率事件是什么.

【例3】厂家在产品出厂前，需对产品做检验，厂家将一批产品发给商家时，商家按合同规定也需随机抽取一定数量的产品做检验，以决定是否接收这批产品.

(Ⅰ)若厂家库房中的每件产品合格的概率为0.8，从中任意取出4件进行检验.求至少有1件是合格品的概率;

(Ⅱ)若厂家发给商家20件产品，其中有3件不合格，按合同规定该商家从中任取2件，都进行检验，只有2件都合格时才接收这批产品，否则拒收.求该商家可能检验出不合格产品数ξ的分布列及期望E(ξ)，并求该商家拒收这批产品的概率.

分析：(Ⅰ)为独立重复试验，利用对立事件概率容易得出；(Ⅱ)从含3件不合格品的20件产品中选2件，研究所含不合格品的问题，为超几何分布.

解:(Ⅰ)记“厂家任取4件产品检验，其中至少有1件是合格品”为事件A,

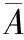
(Ⅱ)ξ可能的取值为0,1,2,

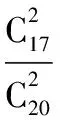
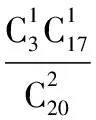
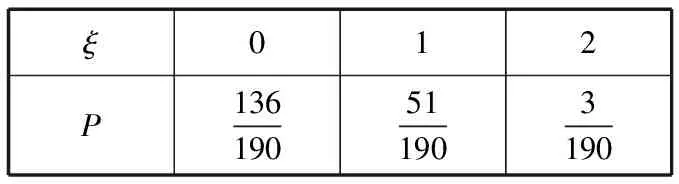
ξ012P136190511903190

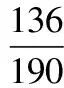
记“商家任取2件产品检验，都合格”为事件B，则商家拒收这批产品的概率

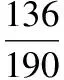
评析：认真分析清楚分布列类型就能正确求解，此题想法并不难，但运算量相对大些，容易在时间紧张时算错，因此在运算时必须讲究技巧，可借助期望的计算公式减少运算量，提高运算的准确率.

三、巧妙借助公式，简化计算提高准确率

概率统计的题目，基本上在分析清楚分布列后都要求计算期望和方差，这是运算量相对较大的地方.熟练掌握二项分布和超几何分布的期望方差公式及其联系，对于提高速度和准确率都是有效的.

解题要点四：在与分布列有关的问题，基本上都涉及期望和方差，因此熟记超几何分布与二项分布的期望和方差公式，对快速正确作答很有帮助.

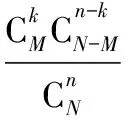
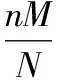
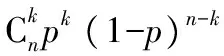
E(X)=np,DX=np(1-p).

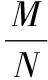
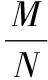
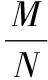
广西合浦廉州中学)