电桥问题整合

安徽 方 林 陶士金

一“桥”飞架南北，突破电学障碍。

电桥问题整合

电桥问题是电学中的复杂问题，近年来有不少电桥问题出现在高考和自主招生试题中，常见的题型有选择题、实验题，也有与平行板电容器结合考查带电粒子在电场中运动的计算题。因此有必要把电桥问题做一小结如下表所示(为讨论方便，不计电源内阻，表中流过各电阻的电流与电阻下标相同)，以帮助考生建立电桥模型。

一、电桥原理分析

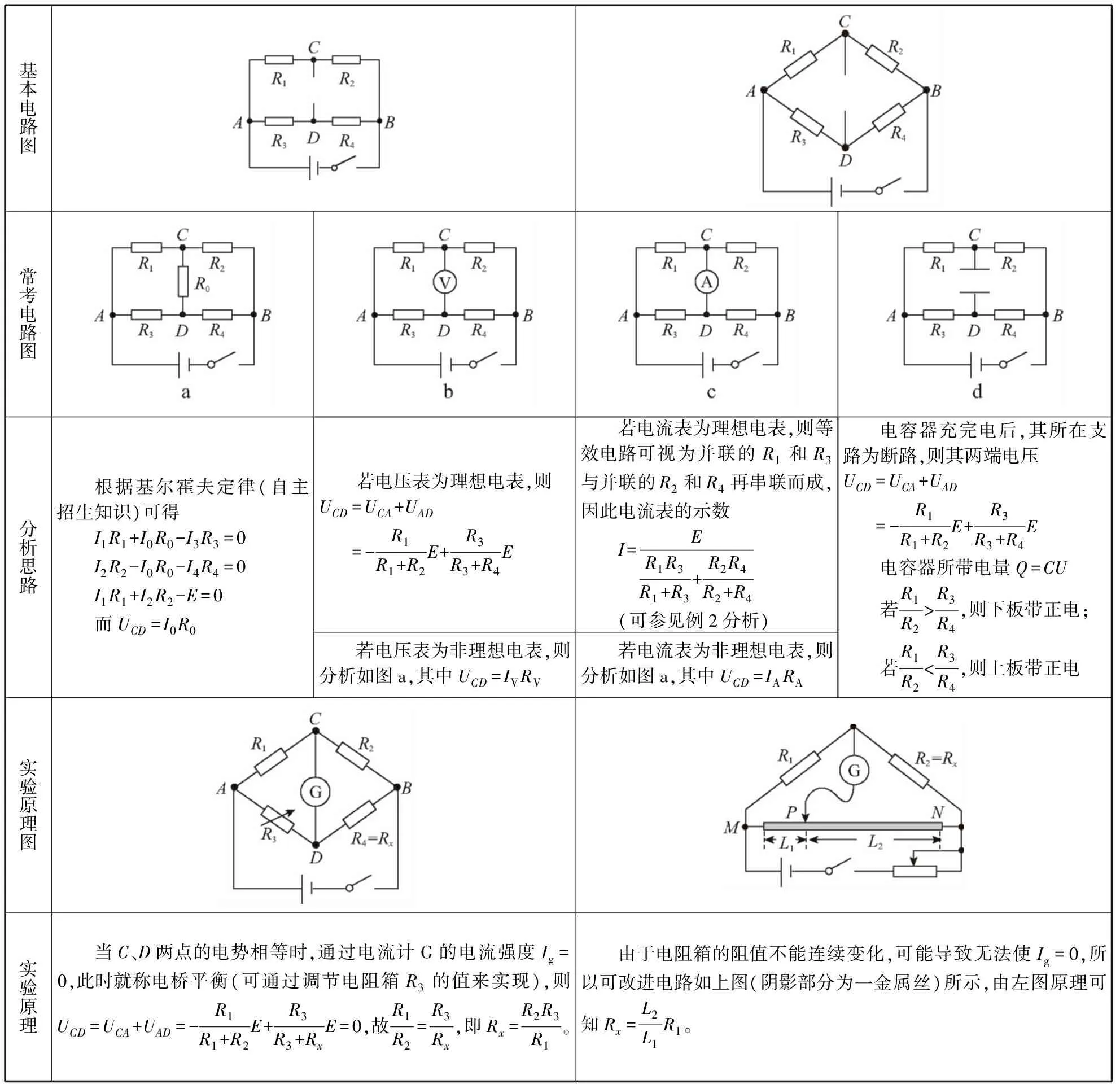
基本电路图常考电路图分析思路 根据基尔霍夫定律(自主招生知识)可得I1R1+I0R0-I3R3=0I2R2-I0R0-I4R4=0I1R1+I2R2-E=0而UCD=I0R0 若电压表为理想电表，则UCD=UCA+UAD=-R1R1+R2E+R3R3+R4E 若电流表为理想电表，则等效电路可视为并联的R1和R3与并联的R2和R4再串联而成，因此电流表的示数I=ER1R3R1+R3+R2R4R2+R4(可参见例2分析) 若电压表为非理想电表，则分析如图a，其中UCD=IVRV 若电流表为非理想电表，则分析如图a，其中UCD=IARA 电容器充完电后，其所在支路为断路，则其两端电压UCD=UCA+UAD=-R1R1+R2E+R3R3+R4E电容器所带电量Q=CU若R1R2gt;R3R4，则下板带正电；若R1R2lt;R3R4，则上板带正电实验原理图实验原理 当C、D两点的电势相等时，通过电流计G的电流强度Ig=0，此时就称电桥平衡(可通过调节电阻箱R3的值来实现)，则UCD=UCA+UAD=-R1R1+R2E+R3R3+RxE=0，故R1R2=R3Rx，即Rx=R2R3R1。 由于电阻箱的阻值不能连续变化，可能导致无法使Ig=0，所以可改进电路如上图(阴影部分为一金属丝)所示，由左图原理可知Rx=L2L1R1。

二、电桥典例分析

【例1】在图1所示的电路中,已知电容C=2 μF,电源电动势E=12 V,内电阻不计,R1∶R2∶R3∶R4=1∶2∶6∶3。闭合开关后，则电容器极板a所带的电量为

( )

A.-8×10-6C B.4×10-6C

C.-4×10-6C D.8×10-6C

【解析】电路稳定后，电容C所在支路为断路，电路等效于串联的R1和R2与串联的R3和R4并联。由串联电路的特点得：

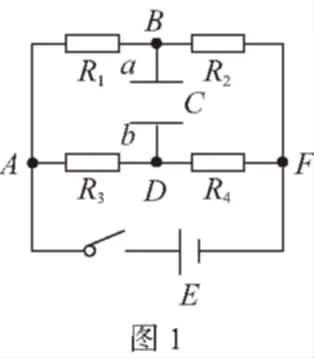
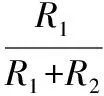
故电容C两端的电压为：

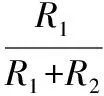
电容器极板a所带的电量为：Qa=CUab=8×10-6C

故选项D正确。

【答案】D

【例2】(2016·江苏卷)如图2所示的电路中，电源电动势为12 V，内阻为2 Ω，四个电阻的阻值已在图中标出，闭合开关S，下列说法正确的有

( )

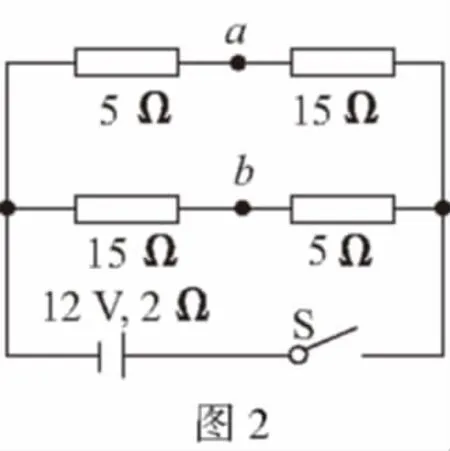
A．路端电压为10 V

B．电源的总功率为10 W

C．a、b间电压的大小为5 V

D．a、b间用导线连接后，电路的总电流为1 A

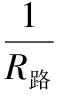
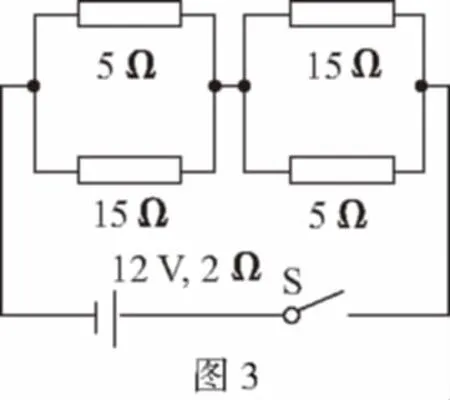
【答案】AC

【例3】(2013·安徽卷)用图4所示的电路可以测量电阻的阻值。图中Rx是待测电阻，R0是定值，G是灵敏度很高的电流表，MN是一段均匀的电阻丝。闭合开关，改变滑动头P的位置，当通过电流表G的电流为零时，测得MP=l1，PN=l2，则Rx的阻值为

( )

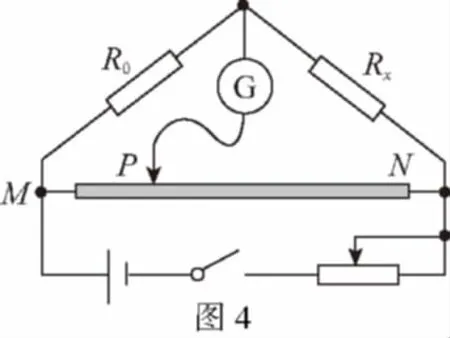
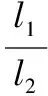
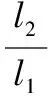
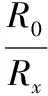
【答案】C

【例4】(2017·全国卷Ⅱ)某同学利用如图5甲所示的电路测量一微安表(量程为100 μA，内阻大约为2 500 Ω)的内阻。可使用的器材有：两个滑动变阻器R1，R2(其中一个阻值为20 Ω，另一个阻值为2 000 Ω)；电阻箱Rz(最大阻值为99 999.9 Ω)；电源E(电动势约为1.5 V)；单刀双掷开关S1和S2。C、D分别为两个滑动变阻器的滑片。