筏架几何参数对隔振系统性能的影响分析

黎上达 ，刘彦

1中国舰船研究设计中心，湖北武汉430064

2船舶振动噪声重点实验室，湖北武汉430064

筏架几何参数对隔振系统性能的影响分析

黎上达1，2，刘彦1

1中国舰船研究设计中心，湖北武汉430064

2船舶振动噪声重点实验室，湖北武汉430064

［目的］为了研究几何参数对浮筏隔振系统性能的影响，［方法］运用参数化建模技术建立筏架的参数化有限元模型，以振级落差作为隔振效果的评价参数。在弹性筏架总质量不变的前提下，分析筏架几何参数对系统隔振性能和筏架固有频率分布的影响。［结果］结果表明：筏架的几何参数对浮筏隔振系统隔振效果的影响主要体现在中、高频段；筏架高度、长宽比、肋板数目是影响浮筏隔振系统隔振性能和筏架固有频率分布最重要的几何参数；调整筏架几何参数是避开机械设备激振频率的有效途径之一。［结论］所得结论对浮筏隔振系统设计具有一定的工程实用价值。

浮筏隔振技术；几何参数；隔振效果；固有频率

0 引 言

舰船内部的主、辅机和轴系等的运转必然产生机械振动，这种振动通过基座传递并激励船体，从而引起船体振动并向周围水介质中辐射噪声［1］。上述现象不利于舰船的安静化，也会恶化舰员的工作和生活环境，因此必须对其进行控制以降低机械振动水平，而目前浮筏隔振是对机械振动进行集中治理（隔离）的主要手段［2～3］。

经过几十年的发展，浮筏隔振相关理论和技术已较为成熟。在实际工程应用中，提高浮筏隔振效果的途径主要包括选择合适的动力参数、合理设计筏架和基座以及优化隔振器布置。在选择合适的动力参数方面，严济宽等［4］以2个柴油发电机组为隔振对象的浮筏隔振系统为例，探讨了系统各主要结构、动力参数对装置隔振、降噪的影响。张华良等［5］通过建立浮筏隔振系统的有限元超单元降阶模型，从隔振传递率的角度研究了筏架质量、刚度和机构阻尼对整个系统隔振性能的影响。在合理设计筏架及基座方面，苏常伟等［6］以某型发电机组浮筏隔振装置及其船体基座为研究对象，探讨了筏架转动惯量、刚度以及基座阻抗对隔振效果的影响。在优化隔振器布置方面，杜奎等［7］运用导纳原理推导了双层减振装置隔振器对齐安装和不对齐安装方案的传递功率流，发现由于结构传递导纳小于输入导纳，不对齐安装更有利于降低宽频率振动的传递。

以上有关浮筏隔振系统的研究说明，选择合理的参数是提高系统隔振效果的有效途径，但这些研究成果主要集中在浮筏隔振系统动力参数选择及其影响上，而筏架几何参数对隔振效果和筏架固有频率分布情况影响等的相关研究工作并不充分。

针对以上问题，本文拟通过建立浮筏筏架的参数化模型，在弹性筏架总质量不变的前提下，采用有限元法分析筏架几何参数对系统隔振性能及筏架固有频率分布情况的影响，希望获得一些有益的结论。

1 建立筏架参数化模型

建立参数化模型是进行参数分析的首要条件。参数化建模是用参数（变量）而不是用数字建立和分析的模型，通过简单的改变模型中的参数值就能建立和分析新的模型。参数化模型有2个层次：参数化几何模型和参数化有限元模型。参数化几何模型往往是实现有限元模型参数化的基础，参数化有限元模型又通常是几何模型中参数作用范围的扩展，并且几何模型不能直接用于分析计算，通常需要将其转化为有限元模型，才能为分析优化程序所用［8］。

目前对浮筏隔振系统进行参数分析或者优化时，建立的参数化模型往往对筏架这一复杂结构进行了大幅度简化，例如：筏架被简化成具有一定厚度的钢平板或具有一定质量的刚体等，通常不涉及筏架结构的几何尺寸参数，这不利于声振传递特性检验计算，不适于筏架结构声学设计。

1.1 筏架结构参数化几何模型

平置板架式浮筏是目前应用范围最广的浮筏结构，根据此类结构形式的浮筏几何体素的特点，可以将其分解为上、下面板和中间正交含腰孔的肋板共3个部分，如图1所示。

图1 平置板架式浮筏架Fig.1 Floating raft with horizontal grillage

按形体分析，浮筏上、下面板可由浮筏筏架的总长、总宽、总高和上、下面板厚度尺寸确定；肋板可由肋板间距、肋板厚度以及肋板腰孔的长、宽尺寸确定（图2）。

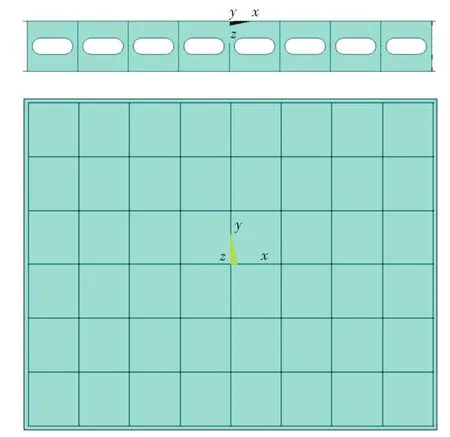
图2 浮筏几何参数Fig.2 Geometric parameters of floating raft

其中，肋板间距受肋板数目控制，因而肋板间距这一定位尺寸可以用肋板数目表示。由此，筏架的所有几何参数如表1所示。修改几何参数的数值即可达到修改筏架大小、形状的目的。

表1 浮筏筏架的几何参数Table 1 Geometric parameters of floating raft

1.2 筏架结构参数化有限元模型

ANSYS参数化设计语言（ANSYS Parametric Design Language，APDL）是一种可以自动完成有限元分析操作或通过参数化变量方式建立分析模型的脚本语言。其参数包括几何尺寸、材料属性、网格尺寸、载荷边界条件等［9］。舰船上使用的浮筏筏架材料一般为钢材，因此，本文不考虑材料参数的影响，重点关注几何参数对隔振效果及其固有频率分布情况的影响。

根据筏架几何参数的初始数值，运用APDL建立使用上述参数表达的有限元模型，如图3表示。筏架均采用Shell 181壳体单元模拟，能较好地模拟其弯曲和剪切变形。

图3 筏架结构参数化有限元模型Fig.3 Parametric finite element model of floating raft

2 几何参数影响分析

以浮筏隔振系统为研究对象，在筏架结构参数化模型的基础上建立浮筏隔振系统有限元模型，进行谐响应分析。浮筏上的动力设备通过上层隔振器与筏架相连，而筏架则通过下层隔振器与基座相连。建模时，采用如下处理方式：动力设备用Mass 21单元等效其质量、转动惯量和惯性矩；动力设备与隔振器之间采用耦合自由度的方式建立连接；所有隔振器均用3个Combine 14弹性阻尼单元模拟其3个方向的刚度和阻尼。此有限元仿真方法的准确性在参考文献［10］中已得到验证。浮筏隔振系统有限元模型如图4所示。

图4 浮筏隔振系统有限元模型Fig.4 Finite element model of floating raft isolation system

隔振效果采用振级落差来评定，这里选用位移振级落差LD，则有

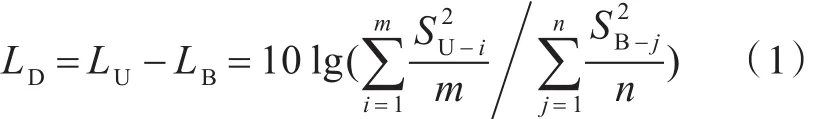
式中：LU为设备机脚处的位移振级；LB为下层隔振器与筏架联结界面上各联结点处的位移振级；SU-i为设备与上层隔振器联结界面上第i个联结节点处的位移响应；SB-j为下层隔振器与筏架联结界面上第j个联结节点处的位移响应；m为上层隔振器数目；n为下层隔振器数目。

由于筏架参数化，则位移振级落差可表示为12个几何参数以及频率f的函数（h），即

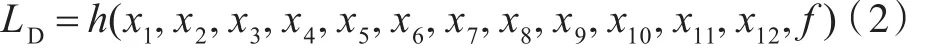
筏架总体积v可表示为12个几何参数的函数（g），故在筏架总质量不变的前提下，可得到以下方程：

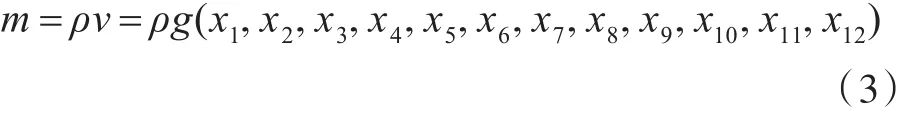
式中：m为筏架总质量；ρ为筏架材料密度；v为筏架总体积。

由式（3）可知，为保持弹性筏架总质量不变，应至少改变两个几何参数的值，例如：本文中的筏架模型增加上面板厚度0.01 mm的同时减小下面板厚度0.01 mm，其他几何参数保持不变，可保持筏架总质量不变。而对筏架进行模态分析时，可将上述浮筏隔振系统中的筏架有限元模型取出，在自由边界条件下计算筏架固有特性，分析筏架几何参数对筏架固有频率分布情况的影响。

由于不同几何参数组合的数目较多，考虑到实际工程应用，且限于篇幅，本文仅选取其中影响较为明显的几种参数组合进行分析，其他的不再赘述。

2.1 不同筏架总长或总宽与总高的组合对隔振效果的影响

通常来说，筏架总长的变化与总宽的变化对隔振系统的影响趋于一致。不失一般性，本文以改变筏架总宽和总高，保持其他几何参数不变的情况为例，分析二者的不同组合对隔振效果的影响，对于改变筏架总长和总高的情况本文不再赘述。图5和表2分别给出了3种不同筏架总宽和总高组合的振级落差曲线和筏架自由状态下的模态频率。

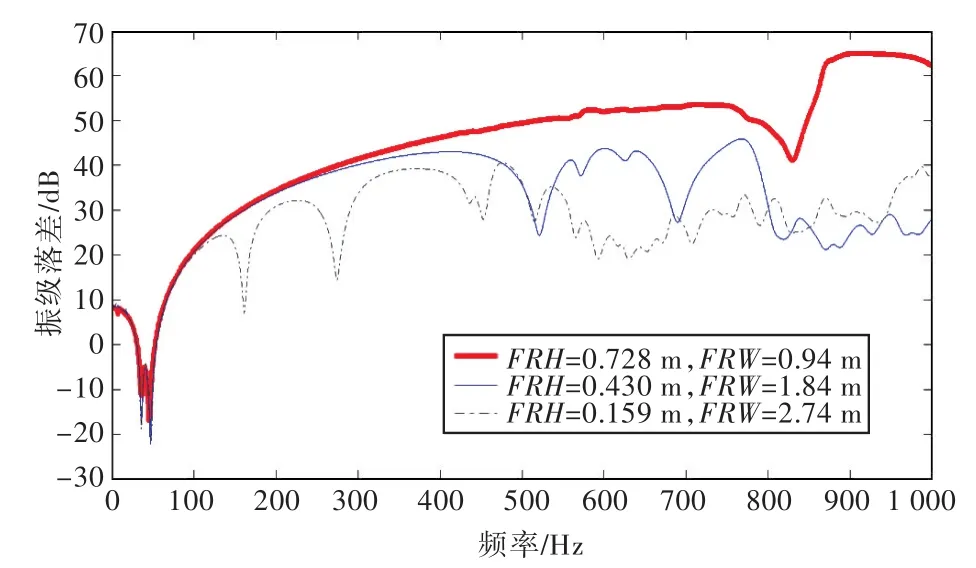
图5 不同筏架总宽和总高组合的振级落差曲线Fig.5 Curves of vibration level difference with FRW and FRH as variables

表2 不同总宽和总高组合时的筏架模态频率Table 2 The natural frequencies of floating raft with FRW and FRH as variables

由图5可知：各振级落差曲线在低频段基本重合，而在中、高频段则相差较大，说明筏架总宽和总高对系统的隔振效果主要体现在高频段；在100～1 000 Hz的中、高频段内，振级随筏架高度的增加而增加，振级落差曲线的波动幅度减小，提高了系统的隔振性能。由表2可知：随着筏架的总高增加和总宽减小，筏架前6阶弹性振动固有频率均向高频移动，说明增大筏架高度可以提高筏架的刚度，减小筏架弹性振动模态密度，提高系统隔振性能。由此可知，筏架总高是影响系统隔振效果最重要的几何参数之一。因此，在实际工程应用中，若条件允许，适当增大筏架总高有利于提高隔振效果。

2.2 不同筏架长宽比对隔振效果的影响

在其他参数保持不变的情况下，仅改变筏架长宽比（RATIO=FRL/FRW），即改变筏架的总长、总宽参数组合，3种不同筏架长宽比时的振级落差曲线和筏架自由状态下的模态频率如图6和表3所示。

图6 不同筏架长宽比的振级落差曲线Fig.6 Curves of vibration level difference with RATIO as a variable

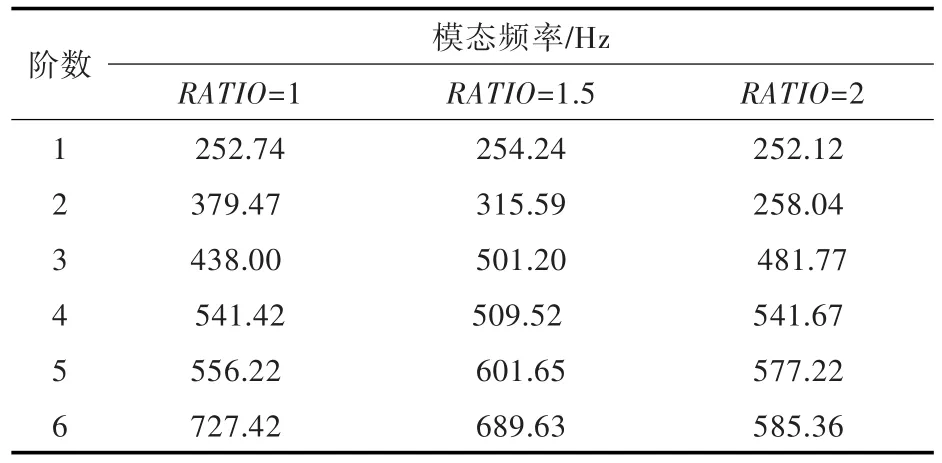
表3 不同长宽比的筏架模态频率Table 3 The natural frequency of floating raft with RATIO as a variable

由图6可知：在低频段，振级落差曲线基本重合，筏架长宽比对系统的隔振效果基本无影响；在中、高频段，振级落差曲线随长宽比的减小而起伏变化。结合表3可知，筏架前几阶弹性振动固有频率并不是随长宽比的增大或减小而同时向高频或低频方向移动。例如，当RATIO=1时，筏架第1，2阶弹性振动固有频率最高，而第3阶固有频率弹性振动最低。因此，调整筏架长宽比能改变筏架弹性振动固有频率的分布，是错开机械设备激振频率的有效手段之一。

2.3 不同总高和肋板厚度组合对隔振效果的影响

在其他参数保持不变的情况下，仅改变筏架总高和肋板厚度，3种不同组合的振级落差曲线和筏架自由状态下的模态频率如图7和表4所示。

图7 总高和肋板厚度变化时的振级落差曲线Fig.7 Curves of vibration level difference with FRH and LBTK as variables

表4 不同总高和肋板厚度组合时的筏架模态频率Table 4 The natural frequencies of floating raft with FRH and LBTK as variables

由图7可知，筏架总高和肋板厚度变化时，虽然低频段的振级落差曲线基本一致，但是在中、高频段，振级随筏架总高和肋板厚度组合的变化，振级落差曲线有明显起伏；在不同的频率区间内，振级落差最大值所对应的曲线也不尽相同。因此，可以根据动力设备的频谱特征，通过调整筏架总高和肋板厚度，达到有针对性的提高隔振系统在特定频段内的隔振效果的目的。

另外，从表4可知，随筏架高度的增大和肋板厚度的减小，筏架前几阶弹性振动固有频率均向高频方向移动，说明筏架总高是影响筏架的刚度和固有频率分布最重要的几何参数之一。因此，调整筏架总高和肋板厚度的组合可以达到调整筏架固有频率分布、提升隔振水平的目的。

2.4 不同长度方向肋板数目和上面板厚度组合对隔振效果的影响

在其他参数保持不变的情况下，仅改变筏架长度方向肋板数目和上面板厚度，3种不同组合的振级落差曲线和筏架自由状态下的模态频率如图8和表5所示。

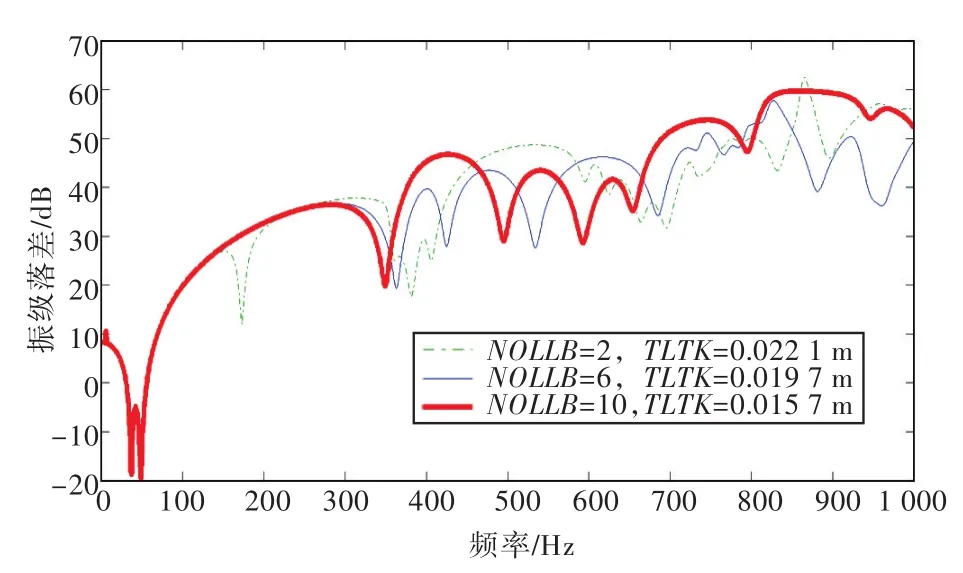
图8 上面板厚度和长度方向肋板数目变化时的振级落差曲线Fig.8 Curves of vibration level difference with NOLLB and TLTK as variables

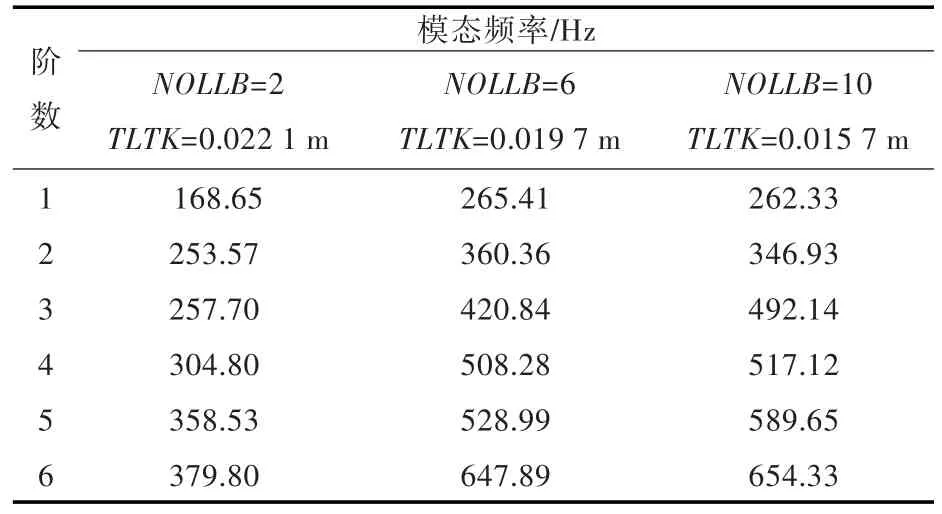
表5 不同上面板厚度和长度方向肋板数目组合时的筏架模态频率Table 5 The natural frequencies of floating raft with NOLLB and TLTK as variables

从图8中可知：肋板数目和面板厚度的变化对于振级落差的影响主要体现在中、高频段。结合表5可知：当肋板数目越多时，虽然上面板厚度减小，但是对应的振级落差曲线波动幅度却呈减弱的趋势，说明适当增加肋板数目可以提高筏架的刚度，减少同频段内筏架局部振动模态的数目，有利于提高浮筏隔振系统在全频段内的整体隔振效果；另外，通过调整肋板数目和面板厚度来改变筏架的首阶固有频率时，首阶固有频率存在极大值，超过极大值后，若继续增加肋板数目，反而会降低筏架首阶固有频率。因此，在筏架结构声学设计中不能以牺牲面板厚度为代价，一味增大肋板数目，应根据机械设备的频谱特征，权衡二者的取值，避开激振频率，以获得优良的隔振效果。

2.5 不同上面板厚度和下面板厚度组合对隔振效果的影响

在其他参数保持不变的情况下，仅改变上、下面板的厚度，3种不同组合的振级落差曲线和筏架自由状态下的模态频率如图9和表6所示。

由图9可知：在低频段，振级落差曲线基本重合，且在高频段，振级落差的曲线变化趋势一致，这说明，改变上、下面板厚度并不能显著提高系统的整体隔振效果。由表6可知：改变上、下面板厚度的组合，可以使筏架的弹性振动固有频率产生小幅偏移。例如，表6中前几阶固有频率的偏移量约为15～22 Hz。另外，当上、下面板厚度相同时，筏架前几阶弹性振动固有频率将达到极大值。因此，在实际工程应用中，若筏架总体尺寸等调整空间不大，改变上、下面板厚度组合也不失为一种调整筏架固有频率分布、避开机械设备激振频率、提高系统隔振水平的途径。

图9 上、下面板的厚度变化时的振级落差曲线Fig.9 Curves of vibration level difference with TLTK and BLTK as variables

表6 不同上、下面板厚度组合时的筏架模态频率Table 6 The natural frequencies of floating raft with TLTK and BLTK as variables

3 结 论

本文运用参数化建模技术建立了筏架的参数化有限元模型，在保持弹性筏架总质量不变的前提下，探讨了筏架几何参数对浮筏隔振系统隔振效果和筏架固有频率分布情况的影响，得出如下结论：

1）在低频段，筏架的几何参数对浮筏隔振系统的隔振效果影响不大，筏架可简化为刚体进行分析计算，可忽略筏架的弹性对隔振系统隔振效果的影响；在中、高频段，筏架的几何参数对浮筏隔振系统隔振效果有较大影响，主要体现在振级落差曲线波动及频移现象上。

2）在条件允许的情况下，尽量增加筏架总高、肋板数目并使总长与总宽尺寸相等，可以提高筏架第1阶弹性振动固有频率，从而有利于提升浮筏隔振系统的隔振性能。

3）根据动力设备的频谱特征，可以通过调整筏架的几何参数，以避开机械设备的激振频率来提高隔振水平。

［1］邵开文，马运义.舰船技术与设计概论［M］.2版.北京：国防工业出版社，2014：719-745.SHAO K W，MA Y Y.Introduction to Technology and Design of Ship［M］.2nd ed.Beijing：National Defense Industry Press，2014：719-745（in Chinese）.

［2］ 游彩霞，张光德，何雪松，等.基于改进FBS理论的浮筏隔振系统计算方法［J］.中国舰船研究，2015，10（1）：109-113.YOU C X，ZHANG G D，HE X S，et al.The calcula⁃tion method of the isolation system based on the im⁃proved FBS theory［J］.Chinese Journal of Ship Re⁃search，2015，10（1）：109-113（in Chinese）.

［3］彭伟才，刘彦，原春晖.机械设备隔振系统的子结构建模方法研究［J］. 中国舰船研究，2012，7（1）：65-70.PENG W C，LIU Y，YUAN C H.FRF-based substruc⁃ture technique for modeling machinery isolation system［J］.Chinese Journal of Ship Research，2012，7（1）：65-70（in Chinese）.

［4］严济宽，沈密群，尚国清.浮筏装置结构动力参数的选定［J］.噪声与振动控制，1995（1）：2-9.YAN J K，SHEN M Q，SHANG G Q.Selection of structural dynamic parameters of floating raft equip⁃ment［J］.Noise and Vibration Control，1995（1）：2-9（in Chinese）.

［5］张华良，傅志方，瞿祖清.浮筏隔振系统各主要参数对系统隔振性能的影响［J］.振动与冲击，2000，19（2）：5-8，4.ZHANG H L，FU Z F，QU Z Q.The effects of parame⁃ters of floating raft isolation system on its isolation char⁃acteristics［J］.Journal of Vibration and Shock，2000，19（2）：5-8，4（in Chinese）.

［6］苏常伟，朱海潮，毛荣富.筏架和基座特性对浮筏隔振效果的影响［J］.舰船科学技术，2014，36（12）：39-42，61.SU C W，ZHU H C，MAO R F.Influences on isolation effectiveness of a generator set and raft vibration isola⁃tion system［J］.Ship Science and Technology，2014，36（12）：36-42，61（in Chinese）.

［7］杜奎，伍先俊，程广利，等.浮筏隔振系统隔振器最佳布置方案研究［J］.海军工程大学学报，2005，17（2）：92-94，99.DU K，WU X J，CHENG G L，et al.Research of best isolation-fixing scheme of floating raft system［J］.

Journal of Naval University of Engineering，2005，17（2）：92-94，99（in Chinese）.

［8］关振群，杜秀云，张洪武，等.考虑结构非线性特征的参数化形状优化方法［J］.机械强度，2003，25（4）：420-425.GUAN Z Q，DU X Y，ZHANG H W，et al.Parameter⁃ization technique for elastic-plastic analysis and shape optimization design of mechanical structures［J］.Jour⁃nal of Mechanical Strength，2003，25（4）：420-425（in Chinese）.

［9］龚曙光，谢桂兰，黄云清.ANSYS参数化编程与命令手册［M］.北京：机械工业出版社，2009.GONG S G，XIE G L，HUANG Y Q.ANSYS parame⁃terized programming and command manual［M］.Bei⁃jing：Machinery Industry Press，2009（in Chinese）.

［10］ 谢志强.基于FEM/BEM的柴发机组水下辐射噪声计算［J］.声学技术，2015，34（2）：438-440.XIE Z Q.Numerical calculation of underwater noise radiation from diesel generator set by FEM and BEM method［J］.Technical Acoustics，2015，34（2）：438-440（in Chinese）.

Effect analysis of geometric parameters of floating raft on isolation performance

LI Shangda1，2，LIU Yan1
1 China Ship Development and Design Center，Wuhan 430064，China
2 Science and Technology on Ship Vibration and Noise Key Laboratory，Wuhan 430064，China

［Objectives］This paper focuses on the effects of the geometric parameters of a floating raft on isolation performance.［Methods］Based on the idea that the weight of a floating raft remains constant，a parametric finite element model is established using geometric parameters，and the effects of the geometric parameters when isolation performance is measured by vibration level difference are discussed.［Results］The effects of the geometric parameters of a floating raft on isolation performance are mainly reflected in the middle and high frequency areas.The most important geometric parameters which have an impact on isolation performance are the raft's height，length to width ratio and number of ribs.Adjusting the geometric parameters of the raft is one effective way to avoid the vibration frequency of mechanical equipment.［Conclusions］This paper has some practical value for the engineering design of floating raft isolation systems.

floating raft；geometric parameters；isolation performance；natural frequency

U661.44

A

10.3969/j.issn.1673-3185.2017.06.016

http://kns.cnki.net/kcms/detail/42.1755.TJ.20171128.1101.012.html期刊网址：www.ship-research.com

黎上达，刘彦.筏架几何参数对隔振系统性能的影响分析［J］.中国舰船研究，2017，12（6）：108-113，119.

LI S D，LIU Y.Effect analysis of geometric parameters of floating raft on isolation performance［J］.Chinese Journal of Ship Research，2017，12（6）：108-113，119.

2017-04-06 < class="emphasis_bold"> 网络出版时间：

时间：2017-11-28 11:01

国家自然科学基金青年科学基金资助项目（61503354）

黎上达，男，1989年生，硕士生。研究方向：振动与噪声控制。E-mail：flexion@126.com

刘彦（通信作者），男，1979年生，博士，高级工程师。研究方向：船舶振动与噪声控制。

E-mail：liuyanhit@gmail.com