双层隔振系统隔振性能分析

赵建学，俞翔，柴凯，杨庆超

1海军工程大学动力工程学院，武汉430033

2海军工程大学科研部，武汉430033

双层隔振系统隔振性能分析

赵建学1，俞翔2，柴凯1，杨庆超2

1海军工程大学动力工程学院，武汉430033

2海军工程大学科研部，武汉430033

［目的］研究准零刚度隔振器各系统参数对隔振性能的影响，可为其应用于隔振系统提供攻关方向。［方法］以线性隔振、准零刚度隔振组成的双层隔振系统和两自由度等效线性隔振系统为对象，分别建立动力学模型；采用平均法推导谐波力激励条件下2个系统的功率流传递率，证明前者比后者有更好的隔振性能，并提出增强双层隔振系统隔振效果的方法。［结果］研究表明，双层隔振系统第2阶共振频率对应的功率流传递率最大值小于1，意味着其在第2阶共振频率附近范围内仍具有隔振效果，从而克服了两自由度线性隔振系统的缺点。［结论］双层隔振系统可通过适当减小阻尼比、质量比和刚度比来提高其隔振性能，且比等效线性隔振系统的低频隔振性能更好。

准零刚度；双层隔振；功率流传递率

0 引 言

由传统隔振理论可知，线性隔振器的起始隔振频率为系统固有频率的 2倍。为实现低频隔振，需减小线性隔振器的刚度，但这会减弱系统的承载能力。由此，国内外学者提出了具有较高静刚度和较低动刚度的准零刚度隔振器［1］，克服了线性隔振器降低固有频率与提高承载力之间的矛盾，具有良好的低频隔振效果［2-3］，在舰船动力设备振动噪声控制领域有着广阔的应用前景。准零刚度隔振器应用于双层隔振、浮筏隔振时，较线性隔振有良好的低频隔振效果和较宽的隔振频带［4-5］。如王心龙等［4］建立了一种带有滚轮装置的双层准零刚度隔振系统的分段非线性动力学模型，并评估了系统隔振性能，结果表明双层准零刚度隔振系统既具有良好的低频隔振性能，又具有较宽的隔振频带。周加喜等［5］将准零刚度隔振器应用于浮筏隔振，构造单层准零刚度隔振浮筏，并评估了系统隔振性能，结果表明准零刚度浮筏隔振的起始频率远低于线性浮筏隔振且隔振效率远高于线性系统。

隔振系统隔振性能的评价指标主要有：振级落差、功率流传递率（插入损失）、力传递率和传递功率流。对于安装在柔性基础的隔振系统，由于在多支承处的传递力在幅值和相位上的差异，功率流传递率或响应比形式的隔振效果评价方法带有一定的缺陷，而且功率流传递率较传递功率流和振级落差更能准确、全面地评价系统隔振效果［6］。因此近年来功率流传递率方法受到越来越多的关注。楼京俊等［7］将基础简化为两端固支的弹性梁并运用机械阻抗法推导了单层柔性隔振系统的传递功率流，通过数值仿真分析了偏心激励对功率流传递特性的影响，将功率流与振级落差频谱曲线进行了比较。夏仕朝等［8］利用四边简支矩形阻尼薄板模拟柔性基础，运用机械阻抗法得到隔振系统的功率流传递公式，讨论了系统各参数对隔振效果的影响。准零刚度隔振系统的隔振效果会受系统参数的影响，因此研究各系统参数对隔振性能的影响可为准零刚度隔振器应用于隔振系统提供攻关方向。

本文将分别建立由线性隔振、准零刚度隔振组成的双层隔振系统和两自由线性隔振系统的动力学模型，根据功率流传递率定义，采用平均法推导谐波力激励条件下2个系统的功率流传递率，运用数值分析方法分析激励力幅值、阻尼比、质量比和刚度比等参数对双层隔振系统功率流传递率及共振频率的影响，提出增强双层隔振系统隔振性能的方法，并对2个系统的功率流传递率进行分析比较。

1 动力学建模与功率流传递率求解

1.1 准零刚度隔振器模型

如图1所示，准零刚度隔振器由1个具有正刚度的竖直弹簧和2个具有负刚度的倾斜弹簧构成［9］。图中：k0，k1分别表示准零刚度隔振器中倾斜弹簧和竖直弹簧的刚度；L0表示倾斜弹簧的长度；h表示系统处于平衡位置时竖直弹簧的压缩量；a表示倾斜弹簧安装位置到系统中心的距离；x表示隔振器的位移。

图1 准零刚度隔振器示意图Fig.1 Schematic diagram of quasi-zero stiffness isolator

当外力F作用于系统时，2个具有负刚度的倾斜弹簧在竖直方向上的力为

在外力F的作用下，准零刚度系统在竖直方向上的力为

将 f0代入式（2），可得

式（3）经无量纲化后，得

由式（6）可知，系统达到准零刚度的条件与竖直弹簧和倾斜弹簧的刚度比β、倾斜弹簧的原长L0，以及倾斜弹簧安装位置到系统中心的距离a有关。

将式（4）在静平衡位置附近进行泰勒展开，得

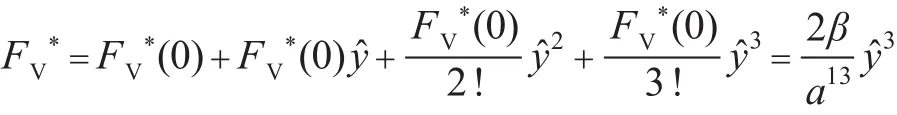
1.2 双层隔振系统

假设基座为刚性，建立双层隔振系统模型如图2所示，其中上层为准零刚度隔振器，下层是线性隔振器。图中：kqzs，k2分别表示准零刚度隔振器非线性刚度和线性隔振器刚度；c1，c2分别表示准零刚度隔振器阻尼和线性隔振器阻尼；Y1，Y2分别表示被隔振设备位移和中间质量块位移；m1，m2分别表示被隔振设备质量及中间质量块质量；FcosΩT表示加在隔振设备上的激励。

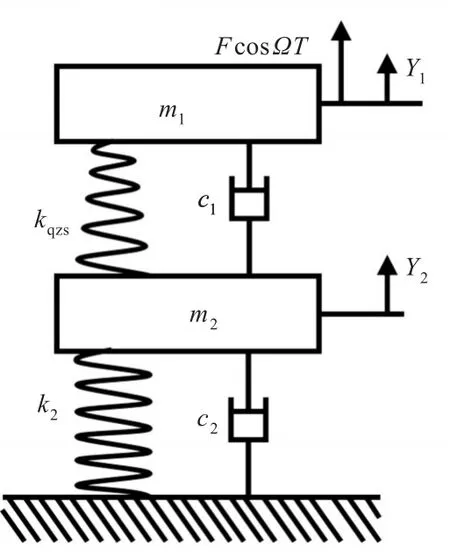
图2 双层隔振系统示意图Fig.2 Schematic diagram of double layer vibration isolation system

以向上为正方向，由图（2）可得

令：

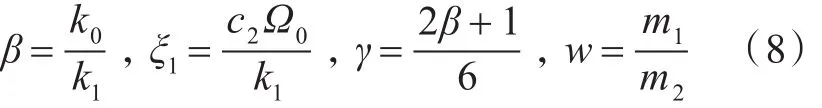
其中，a表示1.1节中负刚度机构左侧安装点距准零刚度隔振器中心的距离。则式（7）转化为无量纲非线性系统模型：

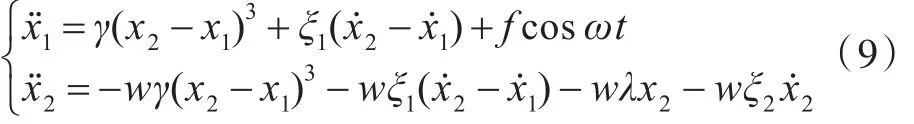
令

则式（9）转化为

式（10）可以转化为矩阵形式：

其中，

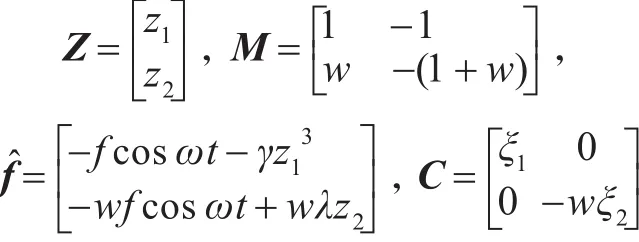
采用平均法［9］，设该系统的稳态响应解为：

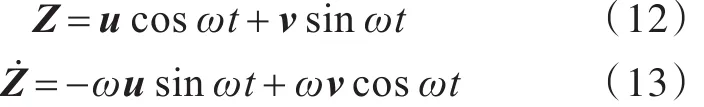
联立式（13）和式（14），可得

将式（12）、式（13）和式（15）代入式（11），得到

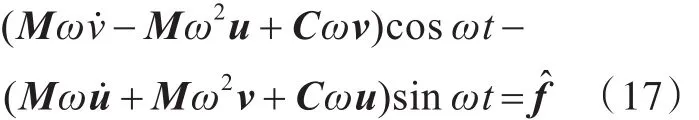
联立式（16）和式（17），得到

式（18）和式（19）的右项可以用 ωt在一个周期中的平均值近似的代替，并认为u和v在ωt的一个周期内保持不变，从而得到平均化方程为：

则式（20）和式（21）可分别简化为

其中，

令式（22）和式（23）的左项等于0，则系统的稳态响应解可以用下面含有v1，v2，u1和u2的多项式表示：

当该系统受到谐波力激励FcosΩT时，传递到中间质量块的无量纲力为

将式（12）和式（13）代入式（28），解得

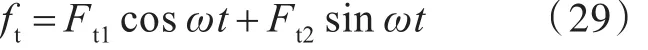
其中，

则传递到中间质量块的无量纲力 ft的幅值Ft可以表示为

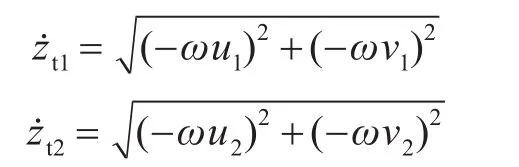
根据功率流传递率的定义［10］，得到双层隔振系统的功率流传递率为

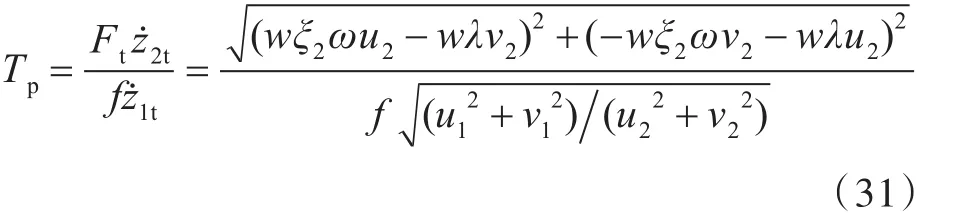
1.3 两自由度线性隔振系统

假设基座为刚性，建立两自由度线性隔振系统模型，如图3所示。k1，k2分别表示上、下层隔振器刚度；c1，c2分别表示上、下层隔振器阻尼；Y1，Y2分别表示被隔振设备位移和中间质量块位移；m1，m2分别表示被隔振设备质量及中间质量块质量；FcosΩT表示加在隔振设备上的激励。弹簧k1的外半径为r。

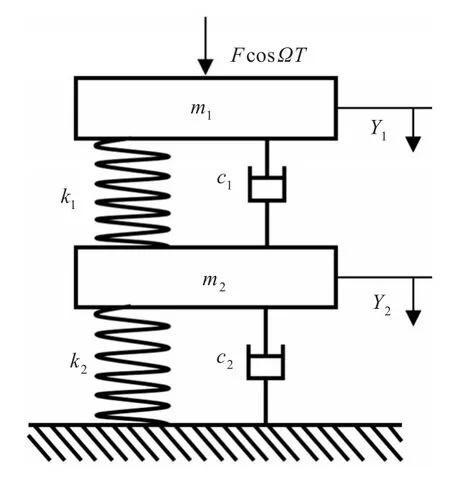
图3 两自由度线性隔振系统示意图Fig.3 Schematic diagram of two degree of freedom linear vibration isolation system

以向下为正方向，由图3可得

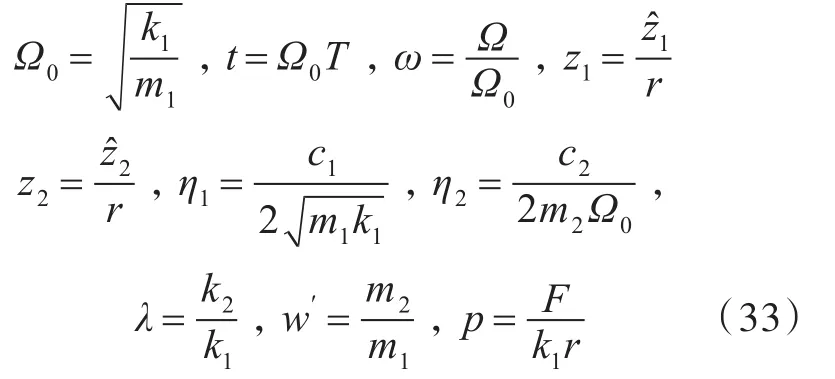
得到系统的无量纲运动微分方程

则式（34）可以化为矩阵形式：

其中，

采用与1.2节中相同的步骤，可以用以下含有v1，v2，u1和u2的多项式表示系统的稳态响应解：

其中，

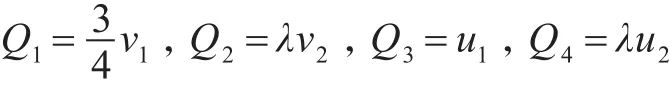
当系统受到谐波力激励FcosΩT时，传递到中间质量块的无量纲力为

解得

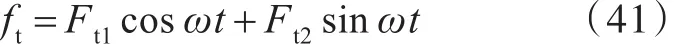
其中，

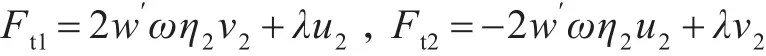
则传递到中间质量块的无量纲力 ft的幅值Ft为

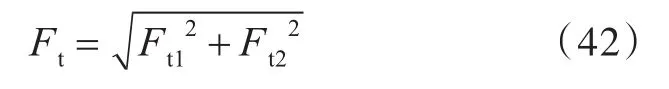
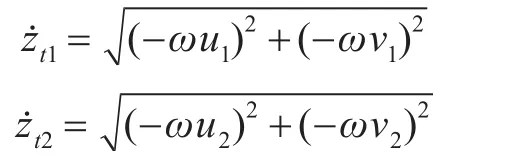
根据功率流传递率的定义，得到两自由度线性隔振系统的功率流传递率为

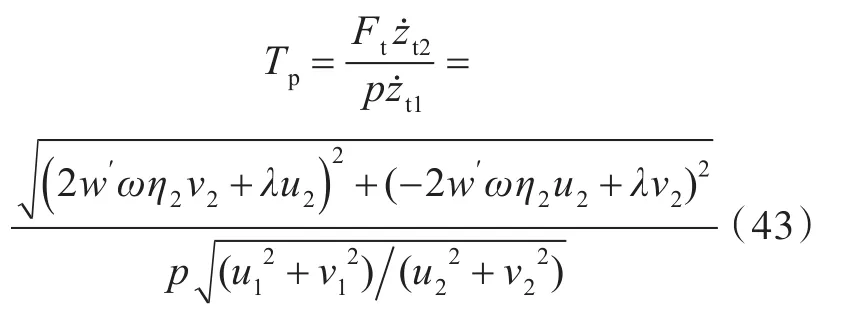
2 功率流传递率特性研究

2.1 激励幅值对系统功率流传递率的影响

当双层隔振系统质量比、阻尼比、刚度比一定时，不同激励力幅值 f条件下的系统功率流传递率如图4所示。由图4可以看到，系统有2阶共振峰，第1阶对应的振动以被隔振设备m1的运动为主，第2阶对应的振动以中间质量块m2的运动为主，下同。随着激励力幅值的增大，第2阶共振频率保持不变，第1阶共振频率增大且其对应的功率流传递率也增大。而且第2阶共振频率对应的功率流传递率最大值小于1，意味着准零刚度隔振系统在其第2阶共振频率附近范围内仍具有隔振效果。

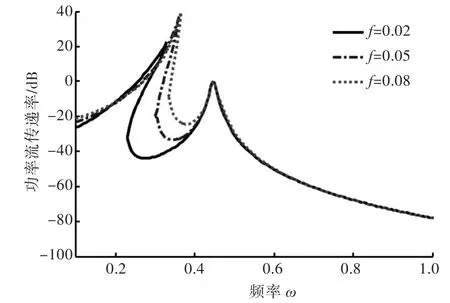
图4 不同激励力 f条件下双层隔振系统功率流传递率参考值Fig.4 The reference values of power transfer rate of double layer vibration isolation system under different excitation forcef

2.2 阻尼比对系统功率流传递率的影响

当双层隔振系统质量比、激励力幅值、刚度比一定时，不同阻尼比ξ1（准零刚度隔振器中弹簧的阻尼比）条件下系统功率流传递率如图5所示。由图5可见，随着阻尼比ξ1的增大，第2阶共振频率及第1阶共振频率对应的功率流传递率均保持不变，第2阶共振频率对应的功率流传递率增大。这意味着可以通过减小阻尼比来增强隔振系统的隔振效果。

图5 不同阻尼比ξ1条件下双层隔振系统功率流传递率参考值Fig.5 The reference values of power transfer rate of double layer vibration isolation system under different damping ratioξ1

当双层隔振系统质量比、激励力幅值、刚度比一定时，不同阻尼比ξ2（线性隔振器中弹簧的阻尼比）条件下的系统功率流传递率如图6所示。由图6可得，随着阻尼比的增大，第2阶共振频率及其对应的功率流传递率均减小。所以可以通过减小阻尼比来增强隔振系统的隔振效果。

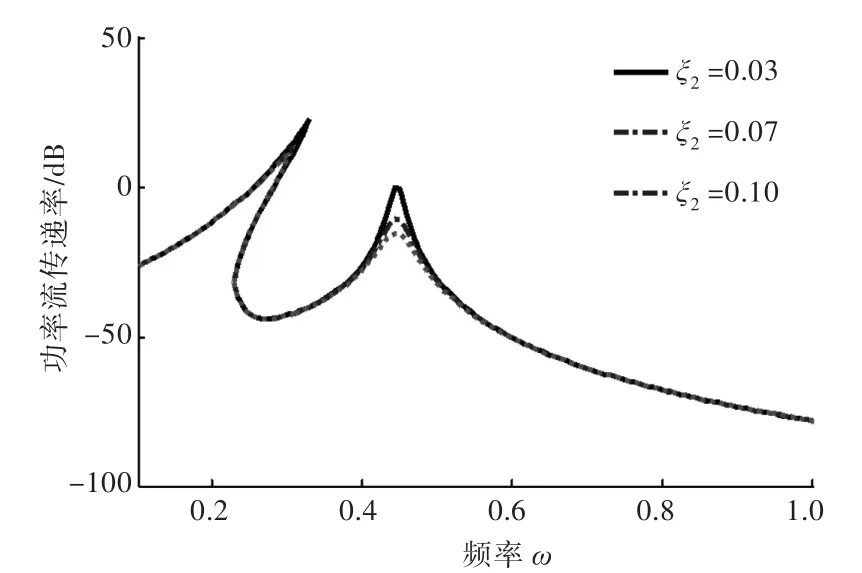
图6 不同阻尼比ξ2条件下双层隔振系统功率流传递率参考值Fig.6 The reference values of power transfer rate of double layer vibration isolation system under different damping ratioξ2

2.3 质量比对系统功率流传递率的影响

当系统的激励幅值、阻尼比、刚度比一定时，不同质量比w条件下两自由度准零刚度隔振系统的功率流传递率曲线如图7所示。由图7可得，随着质量比的增大，系统最大功率流传递率和第1阶共振频率基本保持不变，但第2阶共振频率增大了。所以，可以适当减小质量比，从而减小双层隔振系统的隔振起始频率，增大隔振频率范围，提高其低频隔振性能。

图7 不同质量比w条件下双层隔振系统功率流传递率参考值Fig.7 The reference values of power transfer rate of double layer vibration isolation system under different mass ratiow

2.4 刚度比对系统功率流传递率的影响

当双层隔振系统质量比、激励力幅值、阻尼比一定时，不同刚度比条件下系统功率流传递率如图8所示。由图8可看出，随着刚度比 β增大，双层隔振系统第1阶共振频率及其对应的功率流传递率增大，第2阶共振频率及其对应的功率流传递率不变。所以可通过适当减小刚度比来提高准零刚度隔振系统的隔振性能。

图8 不同刚度比β条件下双层隔振系统功率流传递率参考值Fig.8 The reference values of power transfer rate of double layer vibration isolation system under different stiffness ratioβ

3 双层隔振系统与两自由度线性隔振系统功率流传递率比较

为比较双层隔振系统与两自由度线性隔振系统的隔振性能，令准零刚度隔振器具有正刚度的竖直弹簧和线性隔振器取相同的刚度k1，使2个隔振器具有相同的承载能力。而且2个系统取相同的质量参数 m1和m2，相同的阻尼c1和c2，相同的刚度k2，相同的激励 FcosΩT，由无量纲参数式（8）和式（25），得双层隔振系统的阻尼比 ξ1，ξ2和质量比w与两自由度线性隔振系统的阻尼比η1，η2和质量比w′存在如下关系：

取 ξ1=0.05，ξ2=0.05，w=0.6，则相应的η1=0.025，η2=0.001 5，w′=5/3。等效线性隔振系统激励力对其功率流传递率没有影响，其激励力 p取值为0.1。

从图9可看出，与两自由度等效线性隔振系统相比，双层隔振系统的隔振起始频率更小，隔振频率范围更大，从而具有更好的低频隔振性能。而且，双层隔振系统第2阶共振频率对应的功率流传递率最大值小于1，意味着其在第2阶共振频率附近范围内仍具有隔振效果，从而克服了等效线性隔振系统的缺点。

图9 双层隔振系统与两自由度等效线性隔振系统功率流传递率参考值Fig.9 The reference values of power transfer rate of double layer vibration isolation system and equivalent linear vibration isolation system

4 结 论

本文分别建立了由线性隔振器、准零刚度隔振器组成的双层隔振系统和两自由度线性隔振系统动力学模型，并采用平均法推导了功率流传递率。通过比较分析2个系统功率流传递率，得到如下结论：

1）通过适当减小阻尼比、质量比和刚度比，可以提高双层隔振系统的隔振性能。

2）与两自由度等效线性隔振系统相比，双层隔振系统的隔振起始频率更小，隔振频率范围更大，从而具有更好的低频隔振性能。

3）双层隔振系统第2阶共振频率对应的功率流传递率最大值小于1，意味着其在第2阶共振频率附近范围内仍具有隔振效果，从而克服了两自由度线性隔振系统的缺点。

［1］ ALABUZHEV P，GRITCHIN A，KIM L，et al.Vibra⁃tion protecting and measuring systems with quasi-zero stiffness［M］.New York：CRC Press，1989.

［2］徐道临，张月英，周加喜，等.一种准零刚度隔振器的特性分析与实验研究［J］.振动与冲击，2014，33（11）：208-213.XU D L，ZHANG Y Y，ZHOU J X，et al.Characteris⁃tic analysis and experimental investigation of a vibra⁃tion isolator with quasi-zero-stiffness isolator［J］.Vi⁃bration and Shock，2014，33（11）：208-213（in Chi⁃nese）.

［3］朱石坚，楼京俊，何其伟，等.振动理论与隔振技术［M］.北京：国防工业出版社，2006.

［4］王心龙，周加喜.一种双层准零刚度隔振系统的分段非线性动力学数值分析［C］//2014年中国计算力学大会论文集.贵阳：中国力学学会计算力学专业委员会，2014：1-7.

［5］周加喜，徐道临.单层准零刚度浮筏隔振特性分析及混沌化［J］.中国科技论文，2014，9（8）：911-915.ZHOU J X，XU D L.Vibration isolation and chaotifica⁃tion of quasi-zero stiffness single-layer raft［J］.Chi⁃na Sciencepaper，2014，9（8）：911-915（in Chinese）.

［6］霍睿，施引.功率流隔振效率评价指标及其与振级落差的关系［J］.中国造船，2007，48（3）：86-92.HUO R，SHI Y.The power flow efficiency criterion for vibration isolation design and its relationship with vi⁃bration level difference［J］.Shipbuilding of China，2007，48（3）：86-92（in Chinese）.

［7］楼京俊，李超博，夏江敏，等.柔性隔振系统功率流传递特性分析［J］.船舶工程，2016，38（7）：31-34.LOU J J，LI C B，XIA J M，et al.Research on power flow transmission characteristics of flexible isolation system［J］.Ship Engineering，2016，38（7）：31-34（in Chinese）.

［8］夏仕朝，韩江水，何琳，等.柔性基础隔振系统功率流传递特性［J］.西安科技大学学报，2007，27（3）：419-422.XIA S C，HAN J S，HE L，et al.Power flow transmis⁃sion of vibration isolating system on the flexible founda⁃tion［J］.Journal of Xi'an University of Science and Technology，2007，27（3）：419-422（in Chinese）.

［9］ CARRELLA A，BRENMAN M J，WATERS T P.Stat⁃ic analysis of a passive vibration isolator with quasi-ze⁃ro-stiffness characteristic［J］.Journal of Sound and Vi⁃bration，2007，301（3/4/5）：678-689.

［10］ SUN H L，CHEN H B，ZHANG P Q，et al.Research on performance indices of vibration isolation system［J］.Applied Acoustics，2008，69（9）：789-795.

Vibration isolation performance analysis of double layer vibration isolation system

ZHAO Jianxue1，YU Xiang2，CHAI Kai1，YANG Qingchao2
1 College of Power Engineering，Naval University of Engineering，Wuhan 430033，China
2 Office of Research and Development，Naval University of Engineering，Wuhan 430033，China

［Objectives］Studying the influence of the system parameters of a quasi-zero stiffness isolator on vibration isolation performance can provide a key direction for the application of quasi-zero stiffness isolation in vibration isolation systems.［Methods］Based on a double layer vibration isolation system consisting of linear isolation and quasi-zero stiffness isolation，as well as an equivalent linear vibration isolation system with two degrees of freedom，dynamic models are separately established.Moreover，the average method is applied to derive the power transfer rate under the condition of two harmonic force excitation systems.It is proven that the double layer vibration isolation system has better vibration isolation performance than the equivalent linear vibration isolation system with two degrees of freedom，and a method for enhancing the vibration isolation effect of the double layer vibration isolation system is proposed.［Results］The results show that the power transfer rate of the double layer vibration isolation system is greater than 1 in the second order resonance frequency，which means that it has the effect of vibration isolation in the vicinity of resonance frequencies of the second order，which overcomes the shortcomings of the freedom linear vibration isolation system with two degrees of freedom.［Conclusions］The double layer vibration isolation system can improve vibration isolation performance by appropriately reducing the damping ratio，mass ratio and stiffness ratio，giving it better low frequency vibration isolation performance than the equivalent linear vibration isolation system.

quasi-zero stiffness；double layer vibration isolation；power transfer rate

U661.44；O322

A

10.3969/j.issn.1673-3185.2017.06.015

http://kns.cnki.net/kcms/detail/42.1755.TJ.20171128.1100.010.html期刊网址：www.ship-research.com

赵建学，俞翔，柴凯，等.双层隔振系统隔振性能分析［J］.中国舰船研究，2017，12（6）：101-107.

ZHAO J X，YU X，CHAI K，et al.Vibration isolation performance analysis of double layer vibration isolation system［J］.Chinese Journal of Ship Research，2017，12（6）：101-107.

2017-03-20 < class="emphasis_bold"> 网络出版时间：

时间：2017-11-28 11:00

国家自然科学基金资助项目（51679245）；国家自然科学基金青年科学基金资助项目（51509253）

赵建学（通信作者），男，1992年生，硕士生。研究方向：振动与噪声控制。

E-mail：916082120@qq.com

俞翔，男，1978年生，博士，高级工程师。研究方向：振动与噪声控制。

E-mail：yuxiang898@sina.com