极限思想对无理数的建构

郭龙先

（昭通学院 数学与统计学院， 云南 昭通 657000）

●数学研究

极限思想对无理数的建构

郭龙先

（昭通学院 数学与统计学院， 云南 昭通 657000）

在严格的实数理论建立之前，人们曾直观地将无理数看成是无穷有理数序列的极限，但这在理论上是存在缺陷的.19世纪后期，德国数学家戴德金、康托尔、魏尔斯特拉斯先后创立了各自风格鲜明的实数理论.戴德金的核心思想是对连续性直线的“截断”或“分割”；康托尔则严格地以有理数基本序列构建了无理数；巴赫曼以魏尔斯特拉斯的思想为基础，用区间套对实数作出了定义.20世纪的数学家们，则以公理化思想为基础，建立了公理实数论.

无理数； 闭区间套； 戴德金分割； 康托尔公理； 公理化思想

古希腊数学家很早就发现了既非整数，也不是分数的一种新数——无理数，这是人类数系扩张过程中所遇到的第一个障碍.与自然数向有理数的扩张不同，从有理数到无理数的扩张，是一个“质”的飞跃，它体现了“有限”与“无限”的根本区别.因为把无理数表示成无限不循环小数，实际上是办不到的.这个过程严格来讲，就是用一串有理数（无穷多个）来逼近一个无理数的过程.

在严格的实数理论建立之前，人们曾直观地将无理数看成是无穷有理数序列的极限.但这在理论上是存在缺陷的，因为若该极限本身就是一个无理数，则将导致逻辑混乱.对此，正如弗雷格在《算术基础》一书中所言：“负数和无理数长期以来已为科学所接受，它们的合理性却必须得到更严格的证明.”[1]

19世纪后期，随着数学分析基础的严格化，算术地定义实数的问题，引起了极大的关注.德国数学家魏尔斯特拉斯、戴德金、康托尔、巴赫曼等，先后创立了各自风格鲜明的实数理论.魏尔斯特拉斯提出用递增有界数列的极限来定义无理数；戴德金无理数理论的核心思想是对连续性直线的“截断”或“分割”；康托尔则严格地以有理数序列构建了无理数.1892年，巴赫曼提出了区间套原理.贝尔在《数学大师》一书中写道：

维尔斯特拉斯和戴德金在欧多克斯公元前4世纪停下来的地方重新开始对无理数和实际上对连续的讨论；……康托尔则闯出了一条他自己的新路，力图领悟隐含在连续这个概念中的实无穷本身.[2]

戴德金的观点独树一帜，以几何连续性为基础；魏尔斯特拉斯、巴赫曼和康托尔所依据的原理则是分析性的，是对以满足柯西准则的序列来定义无理数这一普遍思想的深化与发展.

1 用区间套住无理数——魏尔斯特拉斯的实数论

1817年，波尔查诺给出了有界实数集最小上界（即上确界）的定义；1823年，柯西给出了“数列收敛定理”.之后，魏尔斯特拉斯证明了“波尔查诺—魏尔斯特拉斯紧致性定理”.他认识到无理数理论对数学分析基础的重要性，坚持对无理数必须通过不可违反的推理返回到整数上去，直到一切都以整数为基础，按照能够理解的语言陈述清楚为止.对此，弗雷格亦写道：只要对算术的整个大厦的基础的认识还有缺陷，也许就很难能够完全弄清楚负数、分数和复数.［1］2

魏尔斯特拉斯曾用递增有界数列的极限来定义无理数.巴赫曼在1892年出版的《无理数的性质》一书中以魏尔斯特拉斯的思想为基础，第一次用区间套对实数作出了定义.1895年，波莱尔完善并证明了由海涅提出的“有限覆盖定理”.波尔查诺——魏尔斯特拉斯定理，即有界无穷集合必有聚点，与区间套原理是等价的.

所谓区间套，实际上是无穷多个区间，一个套一个，而且这些区间越来越小.考虑以有理数为端点的闭区间，这种有理闭区间套满足：对于所有的且）的问题是，虽然=0，例如在十进位制基础上，即可构造出这样的区间套In，其长为10-n，但也可以是2-n或只要求它小于.对此，还可以引进区间套的等价关系，两个有理区间套[an，bn]和等价的充分必要条件是或者对于一切n来说，不等式成立 .

下述事实被作为定义实数的一个基本几何公理：如果I1，I2，…是一个具有有理端点的区间套序列，则存在一个点x包含于所有的In之中.该公理要求任何一个实数直线上的区间套序列都对应实数直线上唯一一点，这其实是一个连续性公理，它保证实轴上没有空隙存在.作为公理，并不需要从其他数学事实逻辑地推导出来.不难看出，所有这些区间的公共点最多只有一个，因为区间的长度趋于零，而对两个不同的点来说，长度比它们之间的距离还小的区间，不能同时包含它们.

具有有理端点的每一个区间由两个有理数来描述，因此数轴上的每一个点，即每一个实数，能够由无穷多个有理数来准确描述.如果两个不同的区间套序列是等价的，则由它们所确定的实数就是相等的.在这种等价关系之下，可定义实数为有理闭区间的等价类.按此定义，在点和数之间建立了一个完全的对应.显然有理数也都包含在其中，如对任意的有理数r，都有区间套序列代表有理数r.

实际上区间套的观念在数学发展的早期就已经使用，特别是用有理数来逼近无理数时，总是把误差限定在一定范围之中.在这一实数理论中，其实并没有多少新的东西，只不过是对无限十进位小数定义作了一个更为一般的表述罢了.需要注意的是，对于区间套序列来说，强调In都为闭区间是很关键的.否则，如果In表示开区间这时，每一个区间In都包含着下一个区间，并且区间的长度趋向于零，却并不存在属于所有In的点.

用区间套原理定义无理数的好处在于加、乘等运算，以及“大于”“小于”等关系，能立即从有理数域得到推广，而且保持着有理数域中原有的一切规律.从纯形式的观点来看，首先，可以在直线上只作出有理点，然后，定义一个无理点是某个有理端点区间套的一个符号.一个无理点完全由长度趋于零的有理点区间套所描述.这一实数理论的特点，可通过无理数e的定义说明如下：

闭区间序列

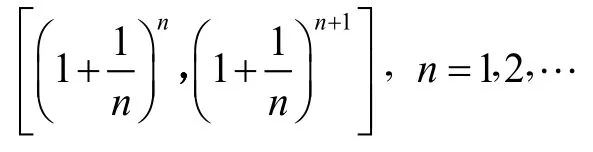
构成一个退缩闭区间套，所以可以把这些区间的唯一的公共交点定义为e，即

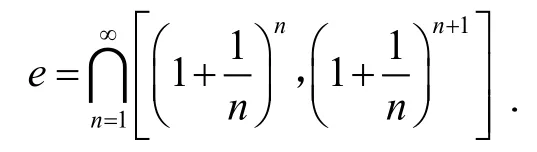
2 连续的秘密在于把直线截断——戴德金的实数论

戴德金作为数学大师高斯的关门弟子，在瑞士苏黎世综合工业学院讲授微积分时，深感分析基础的薄弱，开始了实数理论的研究，并于1872年出版了《连续性与无理数》一书.戴德金认为“必须要有连续性的一个精确定义，使它可以成为逻辑推理的基础.”他首先提出了几何连续性的问题，把直线与实数对应起来，彰显了有理数的稠密性与实数的连续性的区别.戴德金把直线上的点分割成两类，使其中一类的每一个点位于另一类中每一个点的左侧，在这样划分下，有且只有一个点产生，这就是关于直线连续性的戴德金公理，它深刻揭示了直线连续的本质.对此，柯朗写道：

事实上，戴德金证明了这样一点：从费尔马和牛顿到高斯和黎曼，一切大数学家采用的“朴素的”方法，是沿着一条正确的道路前进的.[3]

戴德金无理数理论的核心是他的“截断”或“分割”概念.在他提出的把有理数系分成两类的“分割”理论中，第一类A1的所有数都小于第二类A2的数，并用（A1，A2）表示这样的分割.若A1中存在最大数，或者A2中有最小数，则有且只有这样的分割才是由一个有理数确定的.

但并非所有的分割都是由有理数确定的，如果A1中不存在最大数，A2中也没有最小数，那么戴德金就称这个分割定义了一个无理数，或者简单地说这个分割是一个无理数.例如A1是所有负有理数、零和所有平方小于2的正有理数，A2是所有平方大于2的正有理数，则这个分割就不是由有理数确定的（其实就是）.戴德金通过这样的分割，“创造出一个新的无理数α来，它是完全由这个分割确定的.”

戴德金提出的“分割”概念，作为“人类心智的自由创造”，是一种大胆而首创的思想，每一个分割中，都必然存在与之对应的唯一的有理数或无理数.笼罩在连续性问题上的种种迷雾，通过在直线上一截为二的分割便烟消云散了.对此，贝尔赞誉道：“真理应该从概念而不是从记号得出来.”戴德金实数理论，因其理论的深刻和简洁性，而具有独特的思想魅力和美学特征.

3 以有理数序列构建无理数——康托尔的实数论

1872年，康托尔将一篇概述了实数理论的关于三角级数方面的文章寄给戴德金，作为答谢，戴德金将自己刚发表的《连续性和无理数》赠与他.从此开始了他们之间的友谊和思想交流.在康托尔最富创造力的时期，戴德金给予过极大的帮助和影响.

康托尔的博士论文中有非常引人注目的名句：“在数学上，提出问题比解决问题更有价值.”在实数理论中，康托尔提出的问题是，在不预先假定无理数存在的条件下，如何建立一个令人满意的无理数理论.为此，他坚持用有理数的无穷序列{an}定义无理数及其顺序关系.康托尔首先定义了基本序列，即：

一个有理数序列a1，a2，…， ak，…，对于给定的任何正有理数ε＞0，总存在一个正整数序数N，使得当m，n＞N时，对任何n及m，恒有：

两个基本序列可能都收敛于同一极限.为此，康托尔定义了在这些集合中的一个等价关系.如果两个基本序列{ak}与{bk}，当k→∞时，则两者等价.他把实数定义为基本序列（a1，a2，…， ak，…，）的等价类，记作a.例如，有理数r可用序列r，r，…，r，…定义；而序列1，1.4，1.41，1.414，…则定义了无理数

利用基本序列可以自然地定义实数的加法、乘法以及它们之间的关系：等于、大于、小于等.这样定义的实数既包含有理数也包含无理数，而且实数构成的基本序列的极限也在实数当中，从而证明了实数系的完备性.康托尔的思想是受到下述事实启发的：

1）实数可以看成一个无限十进位小数；

2）无限十进位小数可以看成有限十进位小数的极限.

如果摆脱对十进位系统的依赖，则可以说：任何一个有理数序列，如果“收敛”的话，就定义为一个实数.由于用有理数序列逼近同一个实数有许多方法，所以，如果在两个收敛的有理数列a1，a2，…， ak，…，和 b1，b2，…，bk，…中，当n无限增大时，an-bn→0，则它们就可以定义同一个实数.显然直线上每一点都有对应的实数，但是，对每一实数，在直线上都有相应的点，则须通过公理才能保证.因此，实数集与直线上的点建立一一对应，被称为康托尔公理.

正如贝尔所言：“从无理数的真正性质去看，似乎在有可能建立一个适当的无理数理论之前，有必要先彻底理解数学上的无穷.在戴德金的分割定义中明显地需要无穷类.这样的类导致了严重的逻辑困难.”对此，柯朗写道：

在哲学上，戴特金的无理数定义涉及一个更高程度的抽象，因为它对确定两类A和B的这个数学规则的性质没有加以限制.康托用一个更为具体的方法来定义实数连续统.虽然，初看起来它和区间套方法或分割方法很不同，但是，用这三种方法定义的数系有相同的性质，在这个意义上说，它与那两个方法中的任何一个都等价.[4]

丹齐克也指出：狄德金分割与康托尔序列的出发点如此相反，所循的道路是那样地不同，而结果却极其一致，……实际上，进一步分析狄德金的程序，就发现这里虽然没有明显地用到无限，却暗含了无限在内.还有一层，利用这原理以决定某一无理数的任何实用方法，都必需使用一种与康托尔的无限序列相类似的工具才能完成.[5]

4 结语：殊途同归——公理实数论

运动与连续的问题最终引起19世纪数学家的疑虑，他们采取多种办法，通过实数的“算术式定义”来消除其中的矛盾.另一方面，受到希尔伯特严格的几何公理化思想的鼓舞，数学家们认识到，只要不涉及矛盾性问题，同样的方法也能应用到实数系，实数的公理化，能为整个分析建立基础并能避免“算术式定义”的复杂性.

在实数理论建立之前，自然数列作为意义确定的数学模式，已由皮亚诺五条公理作出了完整的表述：

（1）元素1是自然数.

（2）若a为自然数，则后继（a+）也是自然数.

（3）任何一个自然数的后继都不是1.

（4）若自然数a与b有相同的后继a+=b+，则a=b.

（5）满足上述4条公理的所有自然数作成唯一的集合.

其中第5条公理称之为“归纳公理”，即肯定了自然数的无限性.从n到n+1，这一步接一步的程序产生了数的无限序列，也构成数学推理的一个最基本的类型（即数学归纳法）的基础.柯朗认为，关于实数的“公理”：

原则上只不过是有关自然数的一些需要证明的定理.实际上，我们已经从认定有理数作为已知元素出发了.因为由自然数构造有理数，以及推出有理数的基本性质，根本不会发生困难.［3］98

按公理方式引入实数，将它的一切基本性质作为公理，被认为比欧几里得几何学的公理系统更简单，因为它只有一类“本原对象”——“实数”，而在实数之间，只有三种“本原关系”：

1）两个实数之间的关系x≤y（也写为y≥x）（“序”）.

2）三个实数之间的关系z=x+y（“加法”）.

3）三个实数之间的关系z=xy（“乘法”）.

建立完整的实数系理论需要17条公理：

R1）存在两个不同的实数.

R2）如果x，y是两个实数，则或者x≤y，或者y≤x.

R3）如果同时有x≤y和y≤x，则x=y；反之亦然.

R4）如果x≤y，y≤z，则x≤z.

R5）x+y+z=x+(y+z) .

R6）y+x=x+y.

R7）存在实数a，使得对每个x，有a+x=x.

R8）对于每个实数x，存在实数x′，使得x+x′=a.

R9） 如 果 x≤y， 则 对 每 个 实 数 z， 有x+z≤y+z.

R10）x（yz）=（xy）z.

R11）xy=yx.

R12）存在实数ε，使对每个实数x，有εx=x.

R13）对于每个不等于a的实数x，存在实数x′，使得xx′=ε.

R14）如果a≤x，a≤y，则a≤xy.

R15）x（y+z）=xy+xz.

对于每个实数 x，按 1·x=x，（n+1）x=nx+x，通过关于n的归纳定义数n·x.

R16）如果a≤x且a≠x，则对每个实数y，存在整数n，使得y≤n·x(“阿基米德公理”).

R17）如果{bk}，{ck}（k≥0）是两个实数无穷序列，满足：对每个k≥0，有bk≤bk+1≤ck+1≤ck.则存在实数x，使对每个k，有bk≤x≤ck(区间套公理)[6]

与实数的算术构造理论相反，实数的公理构造是用公理规定实数，然后再定义整数、正整数直至自然数的.但这些公理的相容性是必须证明的，只要做到这一点之后，由此定义的对象就在数学的意义下存在了.对此，希尔伯特特别强调，反对无限集合存在的论点是站不住脚的.

那么这些公理是怎样产生的呢？策梅罗说：“皮亚诺是如何得到他的基本原理的呢？其实他一点也不能证明这些原理.显然，他只是通过分析在历史上已成定论的一些推理的方式，通过指出这些原理在直观上是很明显的，且为科学所需要，就得到这些原理而已.”对于用公理化方法建立实数理论带来的简洁方便这一好处，罗素幽默地说道：“我们所需要的这种假设方法有很多优点，它一下子就假定那些能从小得多的一组公理推演出来的东西，正如窃取总比诚实劳作来得快一样.”[7]对此，柯朗写道：

原则上我们只承认关于自然数的公理（包括数学归纳法原理）.有理数和实数都是在这个基础上被构造出来的.

正如克莱因所言：“逻辑地定义出来的无理数是一个智慧的怪物”.[8]无理数的各种理论在实质上是十分类似的，除了上面介绍的几种实数理论之外，还可以用其他方法建立相应的理论，其主要变化在于完备性公理等价的命题上.

［1］（德）G.弗雷格.算术基础[M].王路 译，王炳文 校.北京：商务印书馆，1998：11.

［2］（美）E.T.贝尔.数学大师——从芝诺到庞加莱[M].徐源 译.上海：上海科技教育出版社，2004：490.

［3］（美）R.柯朗，F.约翰.微积分和数学分析（第一卷·第一分册）[M].张鸿林，周民强译.北京：科学出版社，2005：7.

［4］（美）R.柯朗.什么是数学[M].左平 译.上海：复旦大学出版社，2005：86.

［5］（美）丹齐克.数科学的语言[M].苏仲湘 译.北京：商务印书馆，1985：146.

［6］（法）让·迪厄多内.当代数学：为了人类心智的荣耀[M].沈永欢 译.上海：上海教育出版社，1999：78.

［7］（美）M.克莱因.数学：确定性的丧失[M].李宏魁 译.长沙：湖南科学技术出版社，1997：219.

［8］（美）M.克莱因.古今数学思想（第4册）[M].北京大学数学系数学史翻译组 译.上海：上海科技出版社，1981：51.

The Construction of Limit Thought for Irrational Numbers

GUO Long -xian
(School of Mathematics and Statistics, Zhaotong University, Zhaotong 657000 China)

Before strict real number theory was established, people regarded the irrational number as the limit of infinite rational sequence intuitively, but it was flawed in theory.In the late nineteenth Century, German mathematician Dadekind、 Cantor and Weierstrass successively created their own real numbers theory.Dadekind's core idea is the quot;cutquot; or quot;segmentationquot;of a continuity line; Cantor constructed irrational numbers strictly by the rational numbers sequence ; Bachman defined the real number with the interval sets on the Weierstrass's thought.In twentieth Century, mathematicians established axiomatic theory of real numbers on the axiomatic thought.

irrational number；closed interval sets；Dadekind cut；Cantor axiom；axiomatic thought

O171

A

2095-7408（2017）05-0001-05

2017-09-15

郭龙先（1965— ），女，云南昭通人，教授，主要从事代数学思想史研究.