对泰勒级数展开倍角公式的单摆周期研究

单长吉，张 瑶，杨海燕，徐 楠，龙 烨

（昭通学院 物理与信息工程学院，云南 昭通 657000）

对泰勒级数展开倍角公式的单摆周期研究

单长吉，张 瑶，杨海燕，徐 楠，龙 烨

（昭通学院 物理与信息工程学院，云南 昭通 657000）

利用泰勒级数对高倍角进行展开，得到一系列单摆周期近似公式，并与已有的单摆周期近似公式进行比较，结果表明：泰勒级数展开的一系列公式精度较高，能够加深对单摆周期涵义的理解.

倍角公式； 泰勒级数； 近似公式； 局部常化

单摆是大学物理中的一个重要实验，但实验用的公式仅适用摆角θ≤5°，摆角大时将产生较大的误差.因此，有必要推导出一些适用于大摆角的周期近似公式.本文将在参考文献[1]-[2]提出的倍角公式方法基础上，利用泰勒级数展开高倍角，从而得到一系列的单摆周期近似公式，并对公式进行讨论.

1 定义脚标

因文中字符较多，特别对文中脚标进行如下定义:Tabc，a为倍角数；b表示为泰勒级数展开的级数，二级展开用数字1来表示，三级展开用数字2来表示；c为待定系数所在公式的序数.如λ411表示：用泰勒级数二级展开的四倍角公式，需要确定的第一个待定系数.

2 预备公式

单摆无阻尼振动的动力学方程为：

角振幅时θ0→0的周期极限为：

正弦函数四倍角到七倍角的公式如下：

3 应用泰勒级数对高倍角展开的单摆周期近似公式推导

以四倍角为例，来说明泰勒级数展开在倍角公式中得应用.将公式（3）局部常化如下：

则其泰勒级数二级、三级展开近似值为：

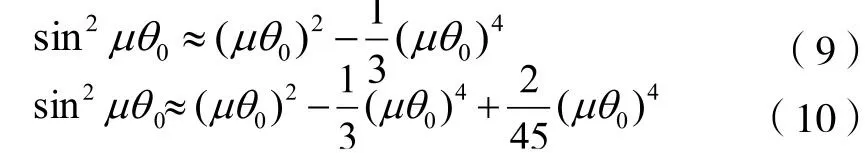
将(7)式局部常化结合（9）式有：

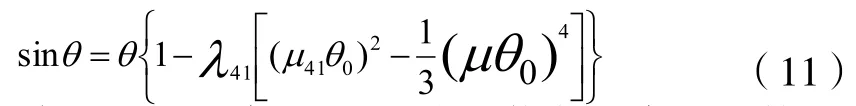
将（11）式代入（1）式四倍角得泰勒级数二级的单摆周期近似公式为 ：

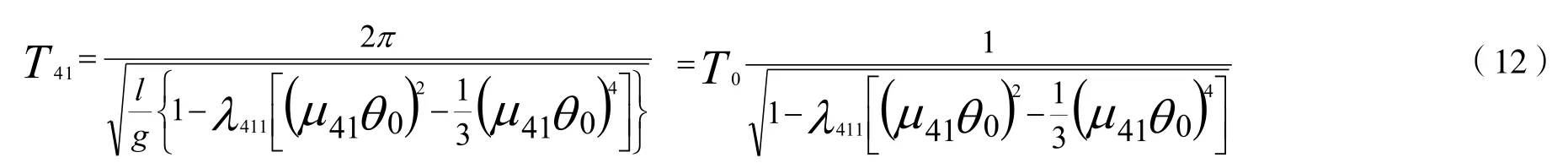
同理将（10）式代入（7）式，综合后代入（1）式得：四倍角泰勒级数三级展开单摆周期近似公式为：

同理，五倍角泰勒级数二级展开的单摆周期近似公式为：

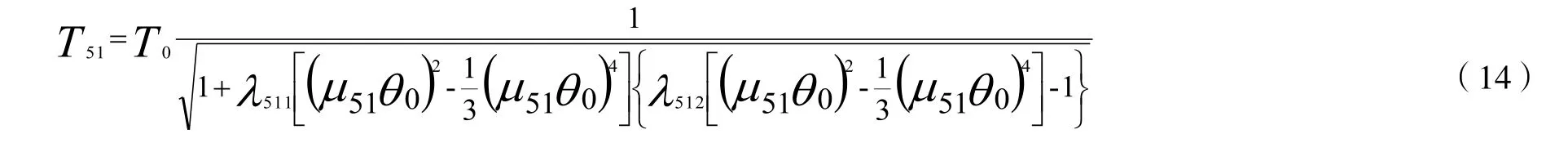
五倍角泰勒级数三级展开的单摆周期近似公式为：

六倍角泰勒级数二、三级展开的单摆周期近似公式分别为：

七倍角泰勒级数二级、三级展开的单摆周期近似公式分别为：

从公式（12）-（19），可以看出需要确定公式中的待定系数[4]-[5].将上述周期公式Tab（a为倍角数；b为泰勒级数展开级数，数字1为泰勒级数二级展开，数字2为泰勒级数三级展开，下同；）改写为的形式，将实测周期T（摆角：间隔：2°；）与T0之比写为利用Matlab软件，求出yab与y的最小二乘法误差为极小值时，相应的 和 就是修正后的待定系数值.

以四倍角为例，来说明待定系数的确定过程.

表1给出了各级倍角采用泰勒级数展开时的待定系数，图1-图8分别为采用泰勒级数展开的各级倍角近似公式与实测值之间的最小二乘法误差图.

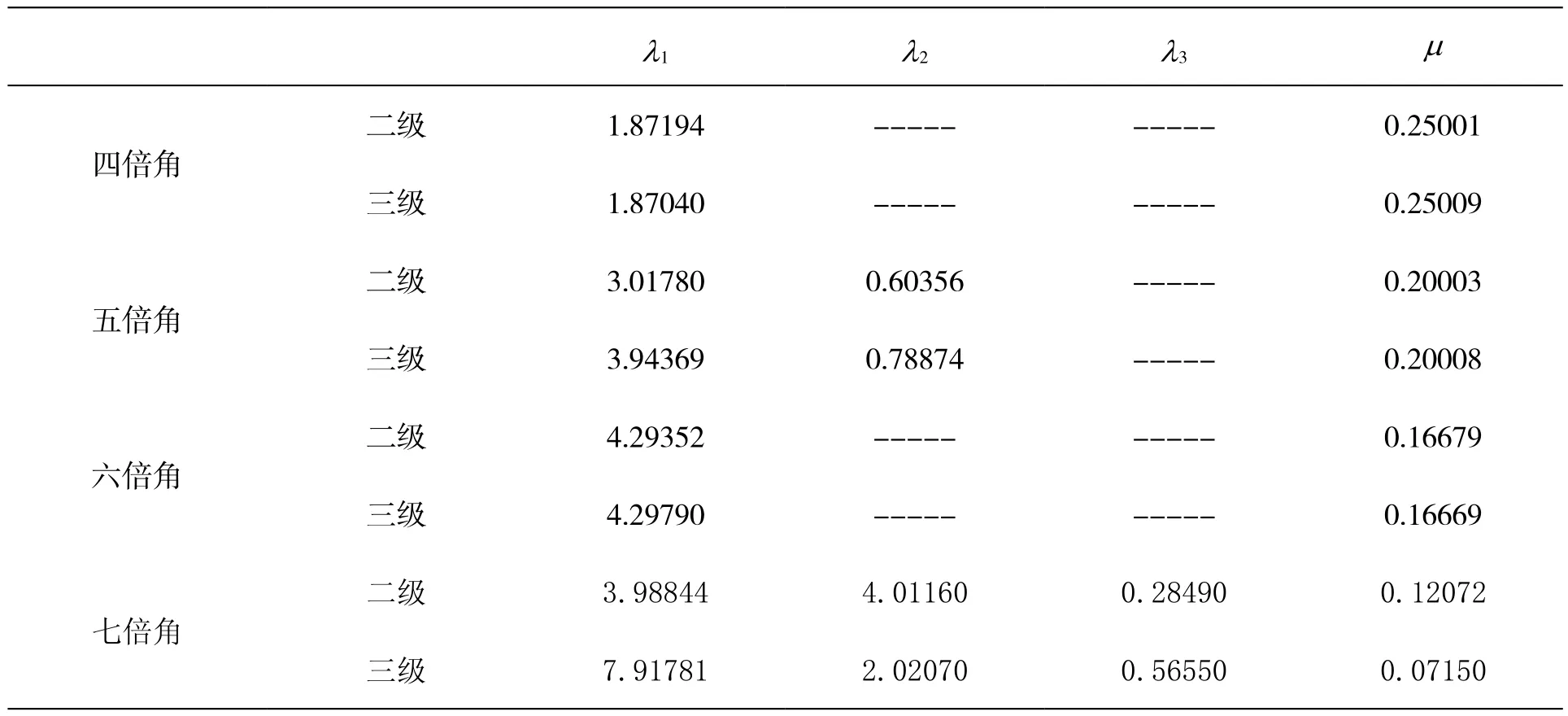
表1.泰勒级数展开待定系数表

图1.四倍角泰勒二级展开误差图

图2.四倍角泰勒三级展开误差图

图3.五倍角泰勒级数二级展开误差图

图4.五倍角泰勒级数三级展开误差图

图5.六倍角泰勒级数二级展开误差图

图6.六倍角泰勒三级展开误差图

图7.七倍角泰勒级数二级展开误差图

图8.七倍角泰勒三级展开误差图

4 泰勒展开的近似单摆周期公式精度比较

表2 利用泰勒级数展开近似公式与实测值误差

从文献[6]中，可知目前已有的部分单摆周期近似公式如下，其形式采用

利用最小二乘法，将（20）式-（27）式与实测值的误差进行比较，图9-图16为误差图，表3为（20）式-（27）式的误差精度.

图9.y1与实测值的误差

图10.y2与实测值的误差

图11.y3与实测值的误差

图12.y4与实测值的误差

图13.y5与实测值的误差

图14.y6与实测值的误差

图15.y7与实测值的误差

图16.y8与实测值的误差

表3 已有公式与实测值的误差

5 讨论

（1）从公式（12）-公式（19）结合表1可以看出，随着倍角的增加，需要确定的待定系数的数目也随之增加；这在客观上增加了推导近似公式的难度.

（2）从图1-图8结合表2可以看出：倍角数相同时，四,六,七倍角数的二级近似周期均比自身三级近似周期精确，五倍角的三级近似周期比二级近似周期精确.

（3）从图9-图16结合表3与表2的比较结果，能够看出用泰勒级数展开倍角推导出的单摆周期近似公式的精度要高于已有的近似公式.

（4）从图1-图16可以看出，误差在4°，6°时较大，这是因为本文采取的与实测值进行比较，由于小角度时存在扭摆，造成误差相对其他组角度时大一些，但并不影响对近似公式的整体评价.

小结

通过利用泰勒级数对高倍角展开，从而得到单摆周期的近似解，为研究单摆周期提供了新的思路，另一方面，对于加深对单摆周期的理解也是大有帮助的.

[1]谭志中.求大摆角单摆周期近似解的“局部常化”方法[J].大学物理，2005,12(24):14-17.

[2]谭志中，罗礼进.用局部常化三倍角公式研究单摆周期[J].大学物理，2007,26(11):25-28.

[3]于凤军，景义林.一个单摆周期近似公式[J].大学物理,2007,26(5):18-19.

[4]单长吉，潘梦鹄，李林，等.用局部常化倍角公式研究单摆周期的讨论[J].高师理科学刊，2011，31（1）：54-56.

[5]鞠衍清，张风雷.单摆运动周期近似公式的数值推导及修正[J].大学物理，2007,26(5)：15-17.

[6]鞠衍清，张风雷.基于MATLAB的单摆周期的比较[J].大学物理，2007,26(3)：6-9.

A Study Of The Simple Pendulum Period of High Angle Formula On Taylor Series Expansion

SHAN Chang-ji, ZHANG Yao, YANG Hai-yan, XU Nan, LONG Ye
(School of Physics and Information Engineering, Zhaotong University, Zhaotong 657000)

A series of single pendulum approximate formula are derived by using Taylor series expansion for the high angle.Though these formulas comparing with the existed approximate formula of single pendulum ,the results show that: a series of formula of high precision Taylor series expansion, can deepen understand for the meaning of the period of single pendulum.

high angle formula; Taylor series; approximation formula; local normalization

O313

A

2095-7408（2017）05-0020-05

2017-03-21

云南省教育厅科学研究基金资助项目 (2014Y499) .

单长吉（1979- ），男，吉林省吉林市人，副教授，硕士，主要从事大学物理教学与科研工作.