范畴表示机器学习算法

徐晓祥 李凡长 张 莉 张 召

(苏州大学计算机科学与技术学院 江苏苏州 215006) (苏州大学机器学习与类脑计算国际合作联合实验室 江苏苏州 215006)

(20154027004@stu.suda.edu.cn)

范畴表示机器学习算法

徐晓祥 李凡长 张 莉 张 召

(苏州大学计算机科学与技术学院 江苏苏州 215006) (苏州大学机器学习与类脑计算国际合作联合实验室 江苏苏州 215006)

(20154027004@stu.suda.edu.cn)

长期以来，人们认为表示问题是机器学习领域的瓶颈问题之一.机器学习方法的性能在很大程度上依赖于数据表示的选择.数据表示领域的主要问题是如何更好地学习到有意义和有用的数据表示.宽泛来看数据表示领域有深度学习、特征学习、度量学习、成分建模、结构化预测和强化学习等.这些技术应用的范围也非常广泛，包括图像、语音识别和文字理解等.因此，研究机器学习表示方法是一件长期且具有探索意义的工作.基于此，利用范畴理论来研究机器学习方法的表示，提出了范畴表示机器学习方法的基本概念.对决策树、支持向量机、深度神经网络等方法进行研究分析，提出了范畴表示分类算法、范畴表示决策树算法、切片范畴表示主成分分析和支持向量机算法、范畴函子表示深度学习方法，给出相应的理论证明及可行性分析.并对这5种算法做了深入分析，找到了主成分分析和支持向量机之间的本质联系，最后通过仿真实验论证范畴表示方法的可行性.

范畴表示；机器学习；机器学习表示；范畴表示学习；范畴表示学习算法

众所周知，机器学习方法的性能很大程度上依赖于数据的表示.表示作为机器学习基本问题之一，一直倍受研究者的关注.表示学习领域的发展速度决定更好的数据表示出现的时间.表示具有广泛的应用领域，主要涉及深度学习[1-3]、特征学习[4-5]、度量学习[6]、核学习[7]、成分模型[8-9]、非线性结构预测[10-11]、非凸优化问题[12-13]等.在2013—2015年举办的学习表示国际会议[14-23]上出现了许多为解决这一问题的思路与方法.这些方法仅是从某类学习方法出发探讨表示问题，而没有给出具有普遍意义的表示方式.如文献[1]从深度学习角度研究文本识别，文献[7]用基于高斯核密度的贝叶斯网络做分类等.并不是从整体普遍的角度来考虑，就分类而言，我们考虑所有的分类算法，如何寻找这些算法的相同点、相异点；寻找到了又如何表达，又如何利用这些相同点、相异点来提高算法效率或者寻找新的算法.为此本文利用范畴理论来研究机器学习方法的一般表示，将现有的以及可能有的机器学习方法包含进范畴表示学习的框架里来给出理论证明，并在文中对几种机器学习方法做了比较详细的研究分析.

综上所述，本文用范畴理论来描述机器学习方法的表示问题有两大优势：1)机器学习表示问题可以转换成输入输出以及它们的关系问题来解决，这符合了范畴的基本思想；2)范畴理论是一个强大且富有兼容性的数学理论，可以将我们现有的以及将有的机器学习方法都用范畴表示，从而进一步利用范畴良好的数学性质来建立机器学习表示理论体系.

1 机器学习方法范畴表示定理

为了便于理解范畴表示学习理论框架，在此给出范畴的基本概念.

1) 一族对象(object)obj,包括样例和实例；

例1. 以集合A={1，2，3}，B={a，b，c}为对象，

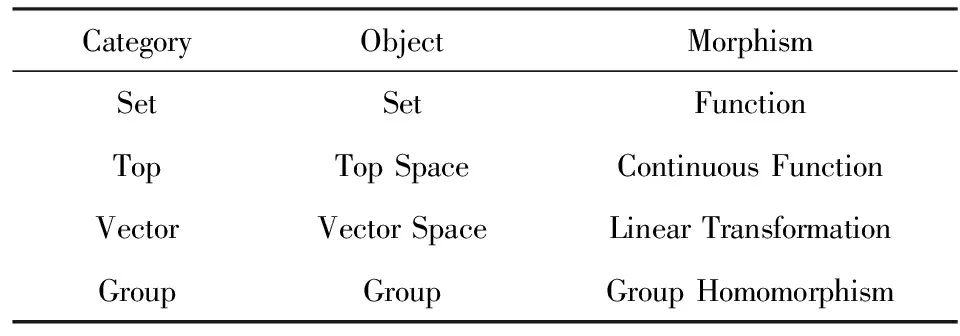
Table 1 Example of Category表1 范畴实例

根据机器学习方法的一般定义：F：X→Y，其中，F表示机器学习方法，X表示样例集合，Y表示实例集合.结合范畴的基本概念，下面给出机器学习方法范畴(categoryofmachinelearningalgorithm,CMLA)的定义.

1) 对象族obj；

定理1. 机器学习方法范畴表示定理(category representation of machine learning algorithm，CRMLA):机器学习方法构成一个范畴.即机器学习方法可用范畴表示.

证毕.

2 范畴表示分类算法

已知集合：C={y1,y2,…,yn}和I={x1,x2,…,xm,…}，确定映射规则y=f(x)，使得任意xi∈I有且仅有一个yi∈C使得yi=f(xi)成立(这里不考虑模糊数学里的模糊集情况).其中，C叫作类别集合，其中每一个元素是一个类别；而I叫作项集合，其中每一个元素是一个待分类项；f叫作分类器.分类算法的任务就是构造分类器f.这就是分类算法的基本思路.

定义3. 分类算法范畴.由2部分组成：

1) 对象族obj={C′,I,…}.其中C′为对应的xi的集合(在实际操作中一般C=C′).

说明：1)这里的对象是分类算法中的各种类别集合与项集合，所有的对象组成对象族；2)态射是对应的分类构成的集合.

证明. 显然存在单位态射，由定义3可知对于任意xi∈I有且仅有一个yi∈C′从而可知：1)每对不同对象之间的态射是不相交的；2)所有态射都为满射，从而满足复合运算率以及结合律.

证毕.

算法1. 范畴表示朴素贝叶斯分类算法.

输入：训练数据X=(x1,x2,…,xn)、类别信息Y=(y1,y2,…,ym)、测试数据x；

输出：类别信息y.

步骤1. 计算每个类别条件下各个特征属性划分的频率：P(x1|y1),P(x2|y1),…,P(xn|y1)；P(x1|y2)，P(x2|y2),…,P(xn|y2)；…；P(x1|ym),P(x2|ym),…，P(xn|ym)；

步骤2. 计算训练样本中每个类别的频率：

P(x|yi)P(yi)=
P(x1|yi)P(x2|yi)…P(xn|yi)P(yi)；

步骤3. y=yi：max(P(x|yi)P(yi)).

结合分类算法范畴以及朴素贝叶斯分类算法，我们不难发现，设f =yi：max(P(x|yi)P(yi))，那么定义朴素贝叶斯算法范畴.在朴素贝叶斯算法范畴中，对象为训练数据X、类别信息Y，那么f：X→Y就是朴素贝叶斯算法范畴的一个态射.

算法2. 范畴表示决策树算法.

输入：E=D1×D2×…×Dm是m维有穷向量空间，其中Di是有穷离散符号集，E中的元素e=(v1,v2,…,vm)叫作例子，其中vj∈Dj,j=1,2,…,m.设PE和NE是E的2个子集，分别叫作正例集和反例集，向量空间E中的PE和NE的大小分别定义为p和n;

输出：决策树 T.

步骤2. 以属性A作为决策树的根所需的期望信息：

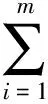
其中pi和ni分别是Ei的正实例和负实例的值；

步骤3. 以A为根的信息增益：

Gain(S,A)=Entrop(S)-Entrop(Si,A)；

步骤4. 选择使Gain(S,A)最大的属性A*，即 Entrop(Si,A)最小，作为根节点；

步骤5. 对A*的不同取值对应的E的k个子集Ei,递归调用步骤1～4过程生成A*的子节点B1,B2,…,Bk，最终生成决策树.

对比算法1与算法2，我们不难发现,最终生成的决策树是决策树算法范畴中的一个态射，并且定义也类似,在此就不进行赘述.但是我们发现：如果在解决同一问题时，那么分别由朴素贝叶斯算法生成的态射和决策树方法生成的态射都属于同一训练数据到类别信息映射集合的一个元素,但是明显可以发现决策树算法的态射比朴素贝叶斯分类算法的态射要复杂得多.这就体现了范畴表示算法的多样性.

算法3. 范畴表示支持向量机算法.

输入：训练数据X=(x1,x2,…,xm)、类别信息Y=(y1,y2,…,yn)、测试数据x；

输出：决策函数g.

在此仅从宏观的分类算法角度来研究支持向量机算法的范畴表示，第3节还会从本质核心的角度来研究，所以仅展示算法的输入输出，具体过程在第3节阐述.

之前已经讲述了2个算法实例，举这2个算法是为了说明范畴表示学习方法的多样性.在此给出第3个算法实例的原因是与第3节用切片范畴表示支持向量机算法做对比，更进一步说明范畴表示学习方法的多样性.由于已经给出了2个算法实例，在此用一句话简略说明支持向量机算法范畴：以训练数据X和类别信息Y作为对象，以决策函数g：X→Y作为其态射的范畴.纵观这3个算法实例，我们可以发现范畴表示学习方法十分简洁精炼，但又可以说明问题.

3 切片范畴表示PCAamp;SVM算法

为了说明如何用切片范畴表示主成分分析(principal component analysis， PCA)和支持向量机(support vector machine, SVM)算法，在此给出切片范畴的基本概念.

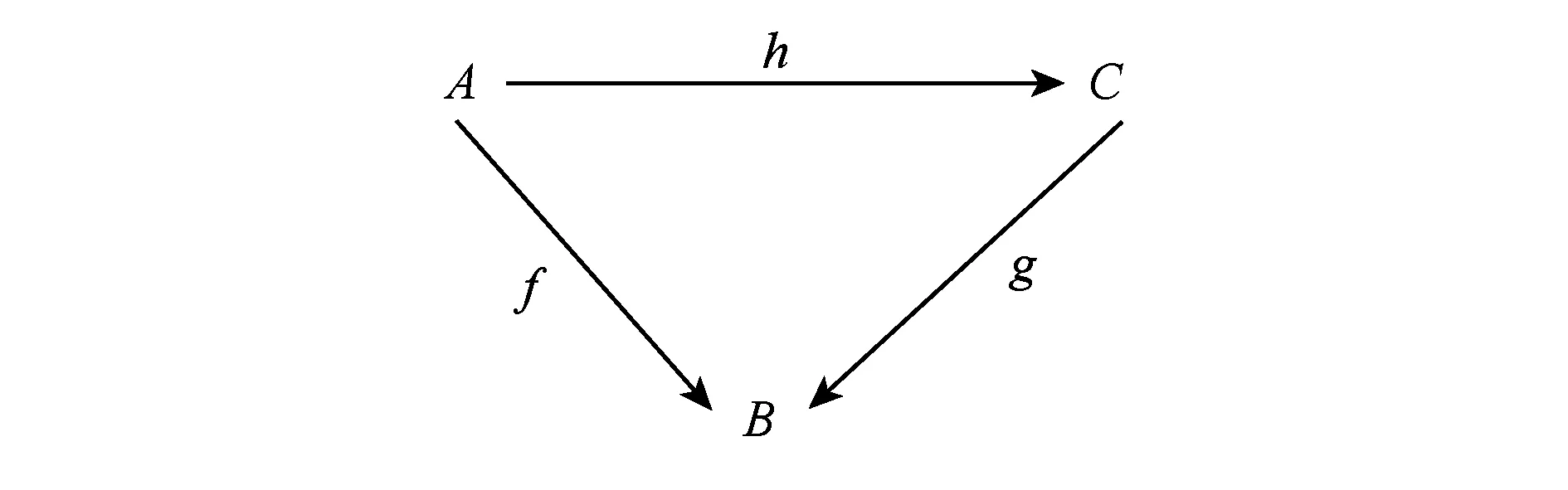
Fig. 1 Slice category over B图1 B上切片范畴

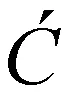
例2. 对象A={a，b，c}，B={1，2，3}，C={●，■，▲}对应态射和切片范畴如图2所示:

f：abc123

morphismg: B→C:

g：■●▲123

SliceCategoryoverB h：A→C：

h：abc■●▲

CosliceCategoryunderB h′：C→A：

h′：■●▲abc

Fig. 2 Morphism and slice category
图2 态射和切片范畴

主成分分析是一种统计分析方法，它可以从多元事物中解析出主要影响因素,主成分分析的目的是将高维数据投影到较低维空间.

算法4. 主成分分析.

输入：原始数据——n行m列矩阵X；

输出：降维数据——k行m列矩阵Z.

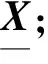
步骤2. 求出协方差矩阵W=1及协方差矩阵的特征λ值和对应的特征向量；

步骤3. 将特征向量按对应特征值大小从上到下按行排列成矩阵W′，取前k行组成矩阵P，Z=PX即为降维到k维后的数据.

支持向量机是一个有监督的学习模型，通常用来进行模式识别、分类以及回归分析.

算法5. 支持向量机.

输入：训练数据X=(x1,x2,…,xn)、类别信息Y=(y1,y2,…,ym)、测试数据x；

输出：决策函数g=wx+b.

步骤1. 原规划max1‖w‖，使得yi(wTxi+b)≥1,其中i=1,2,…,n，即min‖w‖22 使得yi(wTxi+b)≥1,其中i=1,2,…,n；

步骤2. 拉格朗日对偶L(w,b,a)=‖w‖22-其中a=(a1,a2,…,an)为拉格朗日参数；

步骤3. 由拉格朗日对偶求出ai，从而：

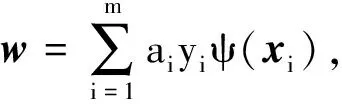
其中，ψ(x)是核函数.

SVM与PCA算法的本质核心都是将数据投影到其他空间，然后利用其他空间的特性来进行处理.但是SVM与PCA不同的是：1)SVM寻找的空间不是低维空间而是高维甚至无限维空间，无法轻易直观地对数据进行表示；2)在PCA中f和g都是不知道具体表达式的，但在SVM中g是已表达的.下面给出切片范畴表示PCAamp;SVM算法示意图，如图3所示：

Fig. 3 Slice category representation of PCAamp;SVM图3 切片范畴表示PCAamp;SVM算法

4 范畴函子表示Deep Learning算法

为了说明如何用范畴函子表示Deep Learning算法，在此给出范畴函子的基本概念.

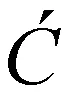
objn→obju：A|→F(A)，
morn→moru：f|→F(f)，

满足dom(F(f))=F(dom(f)),cod(F(f))=F(cod(f))，F(IA)=IF(A).并且若dom(g)=cod(f)，则F(g f)=F(g)F(f).其中,dom为定义域，cod为值域.

DeepLearning算法常见有3种类型：有监督深度学习、无监督深度学习和混合深度学习.监督学习主要用于处理回归和分类问题；无监督学习主要用于处理聚类和密度估计问题；混合深度网络则综合了前2种方式.为了呼应第2节，在此仅以有监督深度学习中的分类算法为例.

算法6. 深度学习算法.

输入：训练数据X={x1,x2,…,xn}、标签数据Y={y1,y2,…,ym}、测试样本x、k层深度网络；

输出：样本标签 y.

步骤1. 预训练，通过最小化损失函数：

J(W,b)=1(2m)×‖h(xi)-xi‖2+
γ2×‖W‖2，

求得W，b，其中xi表示第i个样本，γ为超参数，

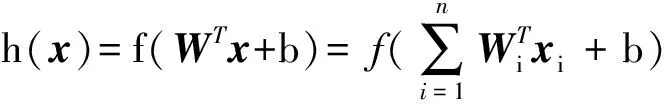
步骤2. 通过最小化交叉熵函数,对W,b进行微调J(W)=-1其中

步骤3. 求出属于第i类的概率Pi：

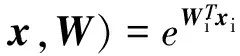
从而y=yi：max Pi.

5 实验仿真

本文进行实验仿真的目的是为了验证范畴表示机器学习方法的可行性，第2～4节中我们对决策树算法、支持向量机算法、深度学习方法进行了理论阐述以及证明.在本节主要针对这3个算法进行可行性验证.

5.1决策树算法实验仿真

在第2节中我们将决策树算法进行了范畴表示，下面就从范畴表示角度进行计算验证算法的可行性.表2为10位志愿者的房产、婚姻、收入、债务情况.我们将以此为例，通过房产、婚姻、收入来预测能否还清债务，并预测第11位志愿者(无房产、单身、收入5.5万元)的债务情况.

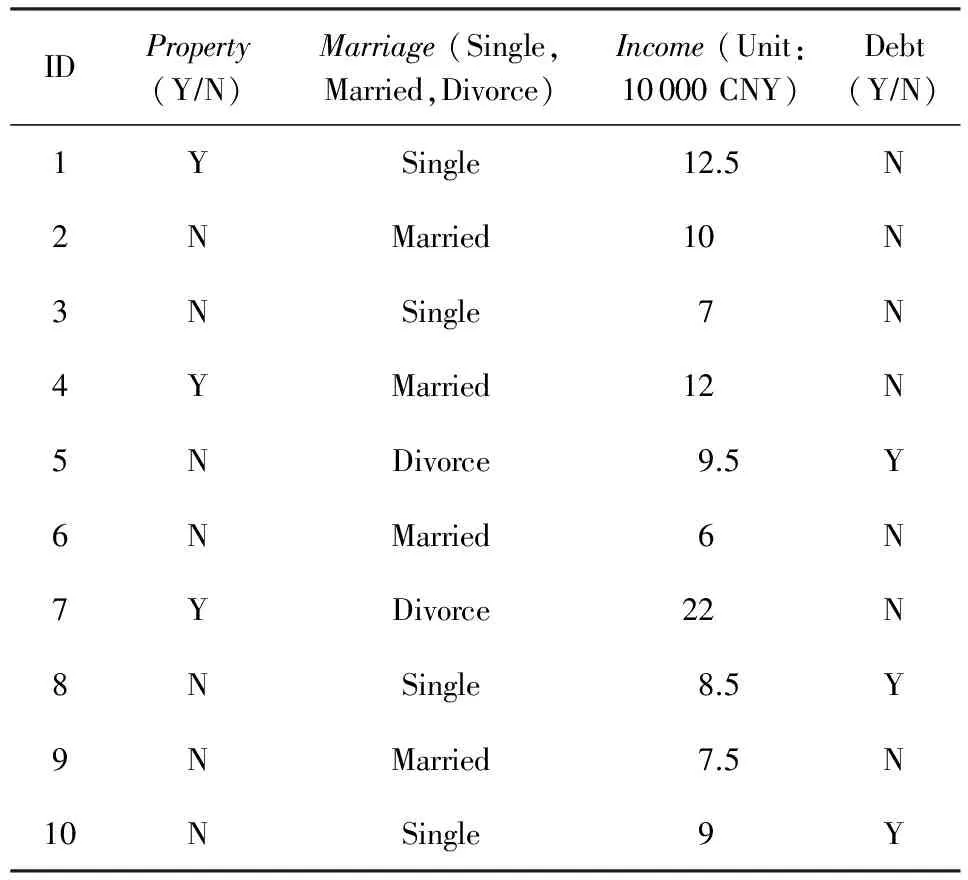
Table 2 Situation of Volunteers表2 志愿者情况

由第2节决策树范畴中的态射构造方法我们可以计算(不妨将收入分为大于等于8和小于8这2类)：

Entrop(S)=-0.3 lb 0.3-0.7 lb 0.7=0.811.
Entrop(PropertyY)=0，
Entrop(PropertyN)=0.985.
Entrop(MarriageSingle)=1，
Entrop(MarriageMarried)=0，
Entrop(MarriageDivorce)=1.
Entrop(Income≥8)=0.985，
Entrop(Incomelt;8)=0.
Entrop(S,Property)=
0.3×0+0.7×0.985=0.69，
Entrop(S,Marriage)=
0.4×0+0.4×0+0.2×1=0.6，
Entrop(S,Income)=0.7×0.985+0.3×0=0.69.
Gain(S,Property)=0.811-0.69=0.121，
Gain(S,Marriage)=0.811-0.6=0.211，
Gain(S,Income)=0.811-0.69=0.121.

从而我们的根节点就是婚姻，重复此过程得到其他分支节点及叶子节点，得到最终态射f如图4所示:

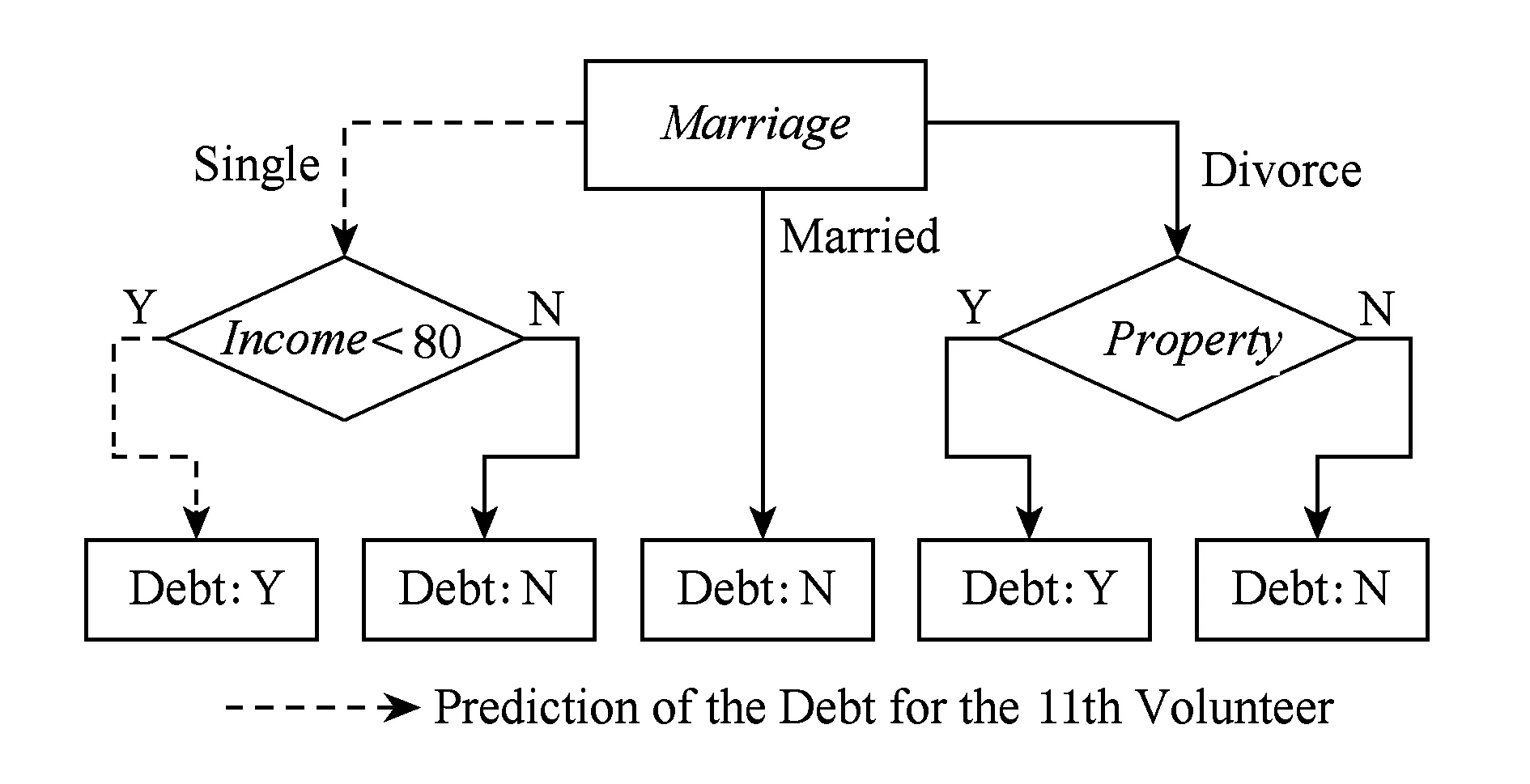
Fig. 4 The morphism f图4 态射f

从而我们的预测第11位志愿者的债务情况为Y(图4中虚线箭头).

5.2SVM算法实验仿真

在第3节中我们将SVM算法进行了范畴表示，下面就从范畴表示角度进行计算验证算法的可行性.实验从人工数据集和ORL人脸数据集上进行验证.

人工数据集(采用线性核)采用服从高斯分布的2组点，分别以(0,0)(2.5,2.5)为中心且标准差为1的2组点，每组100个，进行10次实验取平均准确率为96.57%.其中单次实验效果如图5所示：

Fig. 5 Experimental results on artificial data sets图5 人工数据集实验效果

ORL人脸数据集(采用高斯核) 包含400幅人脸图像(40人×10)，其中每幅图像大小为112×92.其中一半测试一半训练，高斯核参数选取(0.01,128).多分类构建39×40/2个分类器投票决定类别，10次实验平均准确率为93.68%.

由这2组实验不仅验证范畴表示机器学习方法的可行性，同时第1组实验又构成了第2节范畴表示分类算法的一个例子，第1组实验验证了切片范畴表示SVM算法的可行性.结合第1,2组实验发现SVM可用范畴理论来表示体现了范畴表示机器学习方法的多样性.

5.3神经网络算法实验仿真

MNIST数据集[24]是由0～9的手写体数字组成(即10类数据)，包含了60 000张训练图像和10 000张测试图像，每张图像为28×28的灰度图，图6给出了MNIST数据集的一些示例样本.图7为在手写体数据集上196个隐单元的可视化效果.

Fig. 6 Sample for handwritten data set图6 手写体数据集的示例样本

Fig. 7 Visualization of 196 hidden units on handwritten data set图7 在手写体数据集上196个隐单元的可视化效果

COIL数据集[25]包含的样本为日常生活中的一些瓶子、罐子以及盒子之类的物体.该数据集有7 200张灰度图像，共100类数据，每个类别72张图像，每张图像的大小为32×32.图8给出了该数据集的一些示例样本，有100个样本，分别属于不同的类别.图9 COIL数据集上训练所得196个隐单元的可视化效果我们从每个类别中随机地挑选出50张图像，共计5 000张图像作为训练集，剩余的1 200张图像作为测试集.实验中，MNIST和COIL数据均被归一化到了[0,1]之间.

Fig. 8 Sample for COIL data set图8 COIL数据集的示例样本

Fig. 9 Visualization of 196 hidden units on COIL data set图9 COIL数据集上训练所得196个隐单元的可视化效果

本次实验在2个数据集上分别采用深度学习方法，网络的隐单元数均被设为196.MNIST训练样本被随机划分成600批，每批100个样本；COIL训练样本被随机划分成50批，每批100个样本(每一类包含一个数据).最后通过softmax分类器对测试数据进行分类10次实验求平均准确率：在MNIST数据集上为93.03%，在COIL数据集上为98.08%.这不仅验证了范畴表示方法的可行性，同时由可视化效果(图7和图9)可以发现范畴表示方法十分符合人类认知习惯.

6 结束语

本文提出了一种机器学习表示新方法，即范畴表示机器学习方法，并且结合多种机器学习方法来实例验证了机器学习方法表示针对统一性问题的一种可能解法.这种方法包容了所有的机器学习方法，并能对部分方法的本质原理给出依据.因此，本文的创新点主要体现在：

1) 机器学习方法可用范畴表示.不同算法可用同一范畴表示，同一算法可用不同范畴理论表示.这体现了范畴表示机器学习方法的统一性和多样性.

2) 范畴表示机器学习方法能够从表面以及本质上看清算法，同时能够寻找符合人们的认知习惯的表示特征.

范畴表示学习刚刚开始，还有许多工作要做.例如范畴表示学习的拓扑问题、范畴表示学习的流形问题、范畴表示学习的优化问题等.

[1]Belharbi S, Chatelain C, Herault R, et al. Deep structured output learning for unconstrained text recognition[OL]. 2015 [2016-02-06] . https:arxiv.orgpdf1412.5903.pdf

[2]Mao Junhua, Xu Wei, Yang Yi, et al. Deep captioning with multimodal recurrent neural networks[OL]. 2014[2016-02-06] . https:arxiv.orgpdf1412.6632v3.pdf

[3]Goodfellow I J, Vinyals O, Saxe A M. Qualitatively characterizing neural network optimization problems[OL]. 2014 [2016-02-06]. https:arxiv.orgpdf1412.6544.pdf

[4]Liu Tong, Si Yunjuan, Wen Dunwei, et al. Dictionary learning for VQ feature extraction in ECG beats classification[J]. Expert Systems with Applications, 2016, 53: 129-137

[5]Tao Chao, Pan Hongbo, Li Yansheng, et al. Unsupervised spectral-spatial feature learning with stacked sparse autoencoder for hyperspectral imagery classification[J]. IEEE Geoscience amp; Remote Sensing Letters, 2015, 12(12): 2438-2442

[6]Wang Wei, Hu Baogang, Wang Zengfu. Efficient and scalable information geometry metric learning[C]Proc of the 13th IEEE Int Conf on Data Mining. Los Alamitos, CA: IEEE Computer Society, 2013: 1217-1222

[7]Wang Shuangcheng, Gao Rui, Wang Limin. Bayesian network classifiers based on Gaussian kernel density[J]. Expert Systems with Applications, 2016, 51(C): 207-217

[8]Crouzen P, Hermanns H. Aggregation ordering for massively compositional models[C]Proc of the 10th Int Conf on Application of Concurrency to System Design. Los Alamitos, CA: IEEE Computer Society, 2010: 171-180

[9]Virtanen T, Gemmeke J F, Raj B, et al. Compositional models for audio processing: Uncovering the structure of sound mixtures[J]. IEEE Signal Processing Magazine, 2015, 32(2): 125-144

[10]Michel O, Hero A. Tree structured non-linear signal modeling and prediction[J]. IEEE Trans on Signal Processing, 1995, 3(2): 267-270

[11]Patel M, Shah H. Protein secondary structure prediction using support vector machines[C]Proc of the 1st Int Conf on Machine Intelligence and Research Advancement. Piscataway, NJ: IEEE, 2013: 233-244

[12]Parks D, Truszczynski M. Routing non-convex grids without holes[C]Proc of the 1st Great Lakes Symp on IEEE. Piscataway, NJ: IEEE, 1991: 157-162

[13]Ding Yin, Selesnick I W. Artifact-free wavelet denoising : Non-convex sparse regularization, convex optimization[J]. IEEE Signal Processing Letters, 2015, 22(9): 1364-1368

[14]Bribiesca E, Bribiesca-Contreras G. 2D tree object represen-tation via the slope chain code[J]. Pattern Recognition, 2014, 47(10): 3242-3253

[15]Chen Lichi, Hsieh J W, Yan Yilin, et al. Vehicle make and model recognition using sparse representation and symmetrical SURFs[J]. Pattern Recognition, 2013, 48(6): 1143-1148

[16]Fraz M, Edirisinghe E A, Sarfraz M S. Mid-level represen-tation based lexicon for vehicle make and model recognition[C]Proc of the 22nd Int Conf on Pattern Recognition. Piscataway, NJ: IEEE, 2014: 393-398

[17]Liu Haifeng, Yang Zheng, Yang Ji, et al. Local coordinate concept factorization for image representation[J]. IEEE Trans on Neural Networks amp; Learning Systems, 2014, 25(25): 1071-1082

[18]Healy M J. Category theory applied to neural modeling and graphical representations[C]Proc of the 1st Int Joint Conf on Neural Networks. Piscataway, NJ: IEEE, 2000: 30-45

[19]Jadoon W, Zhang Haixian. Locality features encoding in regularized linear representation learning for face recognition[C]Proc of the 2nd Int Conf on Frontiers of Information Technology. Los Alamitos, CA: IEEE Computer Society, 2013: 189-194

[20]Lei Hao, Mei Kuizhi, Zheng Nanning, et al. Learning group-based dictionaries for discriminative image represen-tation[J]. Pattern Recognition, 2014, 47(2): 899-913

[21]Lemus E, Bribiesca E, Garduo E. Representation of enclosing surfaces from simple voxelized objects by means of a chain code[J]. Pattern Recognition, 2014, 47(4): 1721-1730

[22]Liang Yan, Lai Jianhuang, Yuen P C, et al. Face hallucination with imprecise-alignment using iterative sparse representation[J]. Pattern Recognition, 2014, 47(10): 3327-3342

[23]Wang Lingfeng, Yan Hongping. Visual tracking via kernel sparse representation with multikernel fusion[J]. IEEE Trans on Circuits amp; Systems for Video Technology, 2014, 24(7): 1132-1141

[24]Lecun Y, Bottou L, Bengio Y, et al.Gradient-based learning applied to document recognition[J]. Proceedings of the IEEE, 1998, 86(11): 2278-2324

[25]Nene S A, Nayar S K, Murase H. Columbia object image library (COIL-100), CUCS-006-96[R]. New York: Department of Computer Science, Columbia University, 1996

XuXiaoxiang, born in 1991. Doctoral candidate. His main research interests include Lie group machine learning, category theory and homology theory.

LiFanzhang, born in 1964. Professor and PhD supervisor. Senior member of CCF. His main research interests include Lie group machine learning and dynamic fuzzy logic.

ZhangLi, born in 1975. Professor and PhD supervisor. Senior member of CCF. His main research interests include pattern recognition, machine learning and image processing (zhangliml@suda.edu.cn).

ZhangZhao, born in 1984. Professor and Master supervisor. Senior member of CCF. His main research interests include pattern recognition, machine learning, data mining and computer vision (cszzhang@suda.edu.cn).

TheCategoryRepresentationofMachineLearningAlgorithm

Xu Xiaoxiang, Li Fanzhang, Zhang Li, and Zhang Zhao

(School of Computer Science and Technology, Soochow University, Suzhou, Jiangsu 215006) (Joint International Research Laboratory of Machine Learning and Neuromorphic Computing, Soochow University, Suzhou, Jiangsu 215006)

For a long time, it is thought that the representation is one of the bottleneck problems in the field of machine learning. The performance of machine learning methods is heavily dependent on the choice of data representation. The rapidly developing field of representation learning is concerned with questions surrounding how we can best learn meaningful and useful representations of data. We take a broad view of the field and include topics such as deep learning, feature learning, metric learning, compositional modeling, structured prediction, reinforcement learning, etc. The range of domains to which these techniques apply is also very broad, from vision to speech recognition, text understanding, etc. Thus, the research on new representation methods for machine learning is a piece of work which is long-term, explorative and meaningful. Based on this, we propose several basic concepts of category representation of machine learning methods via the category theory. We analyze the decision tree, support vector machine, principal component analysis and deep neural network with category representation and give the corresponding category representation for each algorithms: the category representation of decision tree, slice category representation of support vector machine, and functor representation of the neural network. We also give the corresponding theoretical proof and feasibility analysis. According to further reach of category representation of machine learning algorithms, we find the essential relationship between support vector machine and principal component analysis. Finally, we confirm the feasibility of the category representation method using the simulation experiments.

category representation; machine learning; representation of machine learning; category representation learning; category representation learning algorithm

2016-05-24；

2017-04-07

国家自然科学基金项目(61373093,61402310，61672364，61672365)；苏州大学东吴学者计划项目；江苏省普通高校研究生科研创新计划项目

This work was supported by the National Natural Science Foundation of China (61373093, 61402310, 61672364, 61672365), the Soochow Scholar Program of Soochow University, and the Graduate Innovation and Practice Program of Colleges and Universities in Jiangsu Province.

李凡长(lfz@suda.edu.cn)

TP391