不确定环境下移动对象自适应轨迹预测方法

夏卓群 胡珍珍 罗君鹏 陈月月

1(综合交通运输大数据智能处理湖南省重点实验室(长沙理工大学) 长沙 410114) 2(长沙理工大学计算机与通信工程学院 长沙 410114) 3(国防科学技术大学计算机学院 长沙 410114)

不确定环境下移动对象自适应轨迹预测方法

夏卓群1,2,3胡珍珍1,2罗君鹏1,2陈月月3

1(综合交通运输大数据智能处理湖南省重点实验室(长沙理工大学) 长沙 410114)2(长沙理工大学计算机与通信工程学院 长沙 410114)3(国防科学技术大学计算机学院 长沙 410114)

已有的轨迹预测方法难以对移动对象运动轨迹进行准确地描述,尤其在复杂且不确定的车载自组织网络(vehicular ad hoc network)(也称车联网)环境中.为了解决这一问题，提出基于变分高斯混合模型(variational Gaussian mixture model, VGMM)的环境自适应轨迹预测方法ESATP(environment self-adaptive prediction method based on VGMM).首先，在传统高斯混合模型的基础上使用变分贝叶斯推理近似方法处理混合高斯分布;其次设计变分贝叶斯期望最大化算法学习计算高斯混合模型参数，有效运用参数先验信息得到更高精度预测模型；最后,针对输入轨迹数据特征，使用参数自适应选择算法自动调节参数组合，灵活调整混合高斯分量的个数和轨迹段大小.实验结果表明：所提方法在实验中表现出较高的预测准确性，可应用于车辆移动定位产品中.

环境自适应；变分高斯混合模型；参数自适应选择算法；轨迹预测

智慧城市建设的飞速发展极大地推动了车载自组织网络(vehicular ad hoc network, VANET)(也称车联网)及相关技术的广泛应用.车联网是由车辆位置、速度和路线等信息构成的巨大交互网络.车联网的诞生及发展对于车辆主动安全、智能交通管理、城市生活服务、应急救援等应用具有极大的帮助，而这些应用大都离不开对位置数据的分析与预测.实际交通环境的不确定性给获取移动对象实时空间位置带来了巨大的挑战，如果运动环境突然恶化，通讯信号变得微弱，全球定位系统(global positioning system, GPS)的信号会出现短时中断，致使GPS无法获取实时位置信息.这将造成车辆轨迹数据丢失，影响数据在车联网内传递，信息不能在车辆间共享，最终导致严重的交通事故.在此背景下，本文主要解决的科学问题是：如何在车联网动态环境中移动网络节点(移动车辆)位置复杂多变、网络拓扑频繁变化、交通信息的获取难度增大的情况下，利用车辆历史轨迹数据进行实时轨迹位置预测，为智能交通控制系统提供决策所需的基础数据.

1 相关工作

移动对象轨迹预测算法或模型在近几十年来受到国内外众多专家、学者的关注和研究，取得了诸多成果，并被广泛用于交通、军事、医疗及日常生活服务等多个领域[1-5].如通过分析原始的GPS历史位置数据、预测交通堵塞区域[1]；测量个体轨迹信息熵、预测人类动态行为[2].MyWay建立预测系统，分别使用单个用户行为模型、集体用户行为模型和结合个体与集体行为模型对移动用户下一位置进行预测[3]，该方法的优势在于只需共享个体移动配置文件，简洁地表示用户动作，而不是利用原始轨迹数据揭示用户详细的运动.根据机会路径和目的地原则研究不确定性目的地，提供理想的改道路径到达主要目的地[4].当前，移动对象不确定性轨迹预测方法主要分为基于模式预测方法、基于线性模型预测方法、基于非线性模型预测方法.基于模式的预测方法是通过频繁模式挖掘找出轨迹典型模式，再根据轨迹模式进行预测[6-9].Deb等人[6]提出通过挖掘轨迹频繁模式，找出与数据库中已记录的最频繁路径相匹配的运动模式，进而推断最可能到达的下一个交叉口.该方法由于没有考虑噪声轨迹数据的影响，因此预测精度不高.常用的基于线性模型预测方法主要有基于贝叶斯模型预测方法[10-11]、基于Markov模型预测[12-14]或隐Markov模型预测方法[15-16]、基于多阶Markov模型预测方法[17-18].Schreier等人[11]提出贝叶斯网络中基于操作的长期轨迹预测和驾驶辅助系统危险程度评估方案，有效避免了车辆碰撞.非线性模型预测方法是指通过数学公式刻画移动对象的运动轨迹，其中高斯模型[19-21]是常用的非线性预测模型.Heravi等人[20]结合线性回归分析法和高斯过程回归分析法对长期轨迹进行预测，经证明该方法所提模型参数少且稳定性强，但只适应于小规模数据集.针对复杂运动模式，Wiest等人[21]提出结合贝叶斯网络和高斯混合模型预测车辆将要行驶的路径，该方法预测精度较高且时间开销较低.在本文的后续工作中，借鉴其利用贝叶斯网络处理混合高斯模型来优化模型参数的方法，灵活调整混合高斯部件个数.一些学者利用轨迹的社会关系[22]、轨迹时空信息[23-24]进行预测.上述方法大都只考虑历史轨迹、运动速度、方向、时间、地理特征等因素对预测精度的影响，很少研究动态环境对预测结果的影响.本文针对现有预测方法在动态环境中移动对象轨迹预测精度不高、实时性差的问题提出一种动态环境下自适应轨迹预测方法.本文所提方法通过向传统高斯混合模型引入变分贝叶斯近似推理方法和自适应参数选择算法，自动调节高斯混合模型高斯成分个数组合以适应当前环境，提高预测模型对复杂环境的鲁棒性，维持高精度且时间开销小.

2 移动对象自适应轨迹预测模型

动态环境下移动对象运动轨迹预测，主要包括4个步骤：1)原始位置数据获取，通过车载移动终端收集车辆实时位置信息;2)历史轨迹数据预处理，通过对历史轨迹数据简化、聚类和轨迹分段操作，去除噪声轨迹和提取局部轨迹数据特征；3)轨迹数据建模，对时空轨迹数据进行降维操作、抽取运动模式，构建高效预测模型；4)轨迹在线预测，依据轨迹特征关联，分析移动对象运动趋势并运用预测模型模拟运动轨迹.

2.1轨迹数据预处理

Fig. 1 Chart of trajectory segment algorithm based on density图1 基于密度的轨迹分割算法流程图

由于GPS等移动定位设备接收到的关于移动对象位置信息的原始数据含有大量噪声、冗余数据，不能直接用来进行轨迹预测，因此在使用变分高斯混合模型(variational Gaussian mixture model, VGMM)对轨迹数据建模之前需要预先对位置数据进行预处理操作.首先利用K-Means聚类方法对轨迹数据进行初步聚类，将数据进行分区.鉴于K-Means聚类方法对不规则形状集的聚类效果差，对噪声数据敏感，而基于密度的聚类方法对噪声数据的处理比较好.因此本节接着利用基于密度的聚类方法对轨迹数据进一步聚类处理，去除原始轨迹数据中的噪声数据.基于密度的聚类方法输入邻域半径(Eps)和领域最少数据个数(MinPts)，确定核心点，然后根据点到核心点的距离将数据分类为核心点、噪声点和边缘点，因此将噪声点分离开.其次运用基于密度的轨迹分割算法[9]进一步处理轨迹数据，提取局部轨迹数据特征，提高算法运行的时间效率.本文所提聚类方法的具体实现过程请读者参考文献[25],基于密度的轨迹分割方法采用广度优先搜索策略实现，具体算法流程如图1所示.

2.2基于VGMM预测模型训练

(1)

其中，Z表示隐变量，D为观测数据的维度，(μk,Λk)分别为第k个高斯分量的均值矩阵和精度矩阵.

使用VGMM模型对轨迹数据建模其实质就是要准确估计模型的参数，非高斯噪声模型参数估计常采用变分贝叶斯近似学习方法估计.变分贝叶斯是在传统贝叶斯推断与(examinationmaximum)期望最大化(EM)迭代估计算法的基础上引入变分近似理论而提出的一种学习方法，也叫变分贝叶斯期望最大算法(variationBayesianexaminationmaximum,VBEM)，有效地融合了EM迭代算法收敛速度快、求解过程简单和贝叶斯推断理论利用已有的先验信息等优点，改善了传统高斯混合模型采用EM迭代算法计算模型参数容易陷入局部最优解的不足.假设观测数据集X={x1,x2,…,xN}，N个数据是独立同分布的，已知所有参数的先验分布，隐变量和参数分别由Z={z1,z2,…,zN}和θ={θ1,θ2,…,θN}表示，变分推理对数边缘似然函数可近似表示为[27]

lnp(X)=F(q(Z,θ))+
KL(q(Z,θ)‖p(Z,θ|X))，

(2)

其中：

KL(q(Z,θ)‖p(Z,θ|X))=

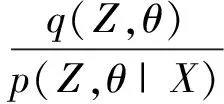
式(2)等号右边第2项KL(q(Z,θ)‖p(Z,θ|X))≥0为q(Z,θ)与p(Z,θ|X)之间的KL散度.要想求得对数似然函数的最小值，需要首先计算KL散度的最小值，然而计算KL散度的最小值难度较大且繁琐，因此，只能计算自由能量F(q(Z,θ))的最大值.

计算隐参数概率(expectationstep,E-step)

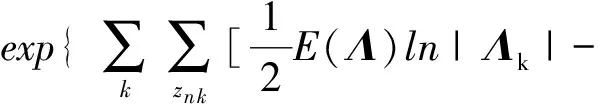
(3)

其中,E(zn k)=rn k.

利用E-step计算得到的隐参数概率来计算变分高斯混合参数联合概率，迭代这2个步骤直到隐参数概率达到最大值，并将取得最大概率时的参数组合为最佳参数组合进行参数更新(maximizationstep,M-step)

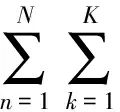
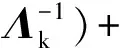
m0,(β0Λk)-1)W(Λk|w0,v0))]，

(4)

其中，参数m0表示先验均值,β0为协方差矩阵梯度系数，W0为先验精度值，v0为威沙特分布自由度初始值.

参数更新：

通过变分贝叶斯近似推理方法处理高斯混合模型求得观测数据集服从近似高斯混合分布：

(5)

其中，mk，ηk分别为第k个分量的均值、精度，其中ηk为

(6)

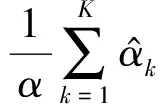
(7)

其中:

).

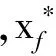
(8)

式(8)为轨迹变分高斯混合回归模型，基本思想是：1)利用式(7)对轨迹数据利用概率密度函数建模，通过基于密度聚类和分割方法对训练轨迹数据进行分析与处理；2)利用变分贝叶斯近似推理迭代计算高斯混合模型参数，依据符合变分高斯混合分布数据的条件分布得到K个高斯分量的回归函数；3)利用式(8)将回归函数加权混合完成轨迹回归预测.

3 基于VGMM的环境自适应轨迹预测算法

3.1工作原理

本文提出的基于VGMM模型的环境自适应轨迹预测算法以变分高斯混合模型为基础，抽象出与VGMM模型相对应的复杂轨迹模式，通过运用变分查询算法解决GMM模型的权重、均值和精度这3个参数的估计问题完成轨迹预测.运用VGMM模型对复杂轨迹运动模式建模的过程中，首先需要对海量位置数据进行分段，将用于训练的轨迹划分成不同的段，用{Si,i=1,2,…,N}表示.同时，采用网格序列表示轨迹化简轨迹，用{Oi,i=1,2,…,K}表示.然后，模型训练学习，利用变分贝叶斯期望最大化法迭代计算模型参数得到近似后验概率分布，设计历史轨迹与未来轨迹的条件概率密度函数.最后运用条件概率密度函数设计未来轨迹关于历史轨迹的回归预测函数.轨迹预测阶段，输入测试轨迹数据集，利用模型训练过程中得到的回归预测函数计算预测值.

3.2参数自适应选择

基于VGMM模型轨迹预测模型选择，与轨迹所在区域大小密切相关.轨迹预测模型的精度主要受VGMM模型参数λ={α,μ,η,v}、轨迹分段的大小segsize这2个因素的影响.在实际应用中，由于运动环境的不确定性，导致移动对象运动状态随时发生改变，因此相邻轨迹点的间隔大小不一致，这就导致了由输入产生轨迹数据丢失的问题.为了解决这一问题，本文采用参数自适应选择算法使得轨迹完整.参数自适应调整过程如下，图2为参数自适应选择算法流程图:

Fig. 2 Flow of parameters self-adaptive selection algorithm图2 参数自适应选择算法流程图

3.3基于VGMM环境自适应轨迹预测

ESATP-VGMM包含2个阶段：1)训练阶段，将经过参数自适应选择算法处理的移动对象历史轨迹数据作为训练数据集，发现轨迹典型运动模式，并以此建立基于变分高斯混合模型的高效预测模型；2)预测阶段，运用训练阶段得到的预测模型对移动对象未来小段时间内运动轨迹进行预测.基于VGMM的环境自适应轨迹预测算法伪代码如算法1所示：

算法1. 基于VGMM的环境自适应轨迹预测算法.

输入：训练数据集 Ttrain=(X,Y)、测试数据集Ttest=(X*,Y*)、轨迹集T={T1,T2,…,Tn}；

输出：轨迹预测平均误差RMSE.

① C=∅, F=∅;

② 分离轨迹点和噪声点，轨迹数据基于密度的聚类得到m个聚类簇并存放到集合C中,C=Tracluster(T);

③ 发现隐藏轨迹点和提取轨迹典型运动模式,基于密度的轨迹分割得到轨迹段集合F=Trasegment(C);

④ 参数自适应选择算法，调整轨迹段大小trasegsize,补充完整轨迹,得到完整轨迹集S=paraselect(F);

⑤ 将轨迹映射到网格中，转换为轨迹链表示transform(S);

⑥ 采用K-Means聚类初始化VGMM模型参数VGMM_para=K-means(Ttrain);

⑦ 模型训练，使用VBEM算法迭代学习估计模型参数M_para=VBEM(Ttrain,VGMM_para);

⑧ 计算轨迹预测步数i=n-d；

⑨ 轨迹预测，Tpr表示预测轨迹点，Tre表示真实轨迹点

fori=1tol

Tpr=predict(M)；

e[i]=callRMSE(Tpr,Tre)；

endfor

由于本章对预测模型学习训练都是通过最优化边缘似然来获取模型所需参数，而每次的梯度计算都要对协方差矩阵求逆，因此所提算法的时间复杂度在模型训练阶段为O(n3L)，n为轨迹数量，L表示梯度计算的次数，轨迹预测阶段的时间复杂度与预测轨迹数量n有关，时间复杂度取值范围为[O(n2),O(nlogn)].

4 实验与结果

本节将使用真实交通场景中车辆位置数据进行一系列的实验，对所提方法的性能进行评估.

4.1数据集与实验环境

本实验数据采用微软亚洲研究院Geolife项目[30]的数据集，包含23 667 828个轨迹点，总长度达1 292 951 km.每个轨迹点包含了移动对象的时空位置信息，本文将轨迹数据集分成2个子数据集，其中训练数据集和测试数据集的分配比例为9∶1.实验使用MATLAB 2014a环境，数据库为SQL Server 2008.实验硬件平台为：Intel®CoreTM2 Duo P8700 2.53 GHz CPU，2 GB内存，操作系统为Windows 7.为了方便比较不同参数条件、不同算法的优劣，性能评价指标使用以下标准，该标注广泛应用于多标签分类研究中[31].

(9)

2) 准确率(accuracy).定义为真正的轨迹点在预测轨迹点集合中出现的频次，如果预测轨迹点就是真实的轨迹点，则p(l)=1，否则p(l)=0.

).

(10)

3) 可信度(reliability).定义为所有的预测轨迹点中概率最大的点不是真实轨迹点出现的频次，如果预测轨迹点是真实的轨迹点，则预测误差e(l)=0，否则e(l)=1.

).

(11)

4) 平均精度(averageprecision).给定预测轨迹点，平均预测精度定义为

其中，p(i)=1表示预测点i是真实的轨迹点.

4.2VGMM模型性能评估

本节对预测模型VGMM模型的性能进行评估.在轨迹预测过程中，合适的选择参数有助于灵活调节参数组合、优化模型性能(比如高斯混合模型混合分量的个数K、轨迹分段大小segtrasize).本节主要研究这些参数是如何影响模型的性能.

首先，研究轨迹段大小β=30的情况下，混合分量个数K从5增加到20的变化对模型的影响.接下来的实验主要测验混合分量个数对预测误差、准确性、平均精度及可信度的影响.图3所示，VGMM获得最好性能，在相同观测轨迹长度下，其预测平均误差在K=15时获得最小，而且随着观察轨迹长度的增加，预测模型预测误差快速下降，高斯混合分量个数在K=15所在曲线表现出明显的优势，最小可达到30 m以下.高斯混合元组个数K对平均精度的影响如图4所示，相同观测轨迹长度下预测模型获得最大平均预测精度在K=15时.

Fig. 3 Prediction error under different observable length of input trajectories图3 不同轨迹长度下混合分量对预测误差的影响

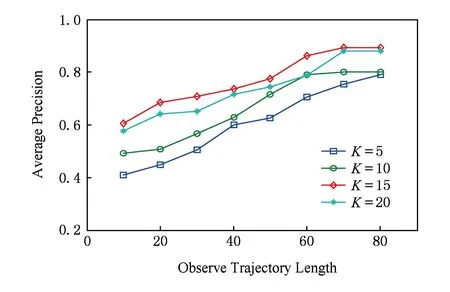
Fig .4 Average precision under different observable length of input trajectories图4 不同输入历史轨迹长度下平均精度比较

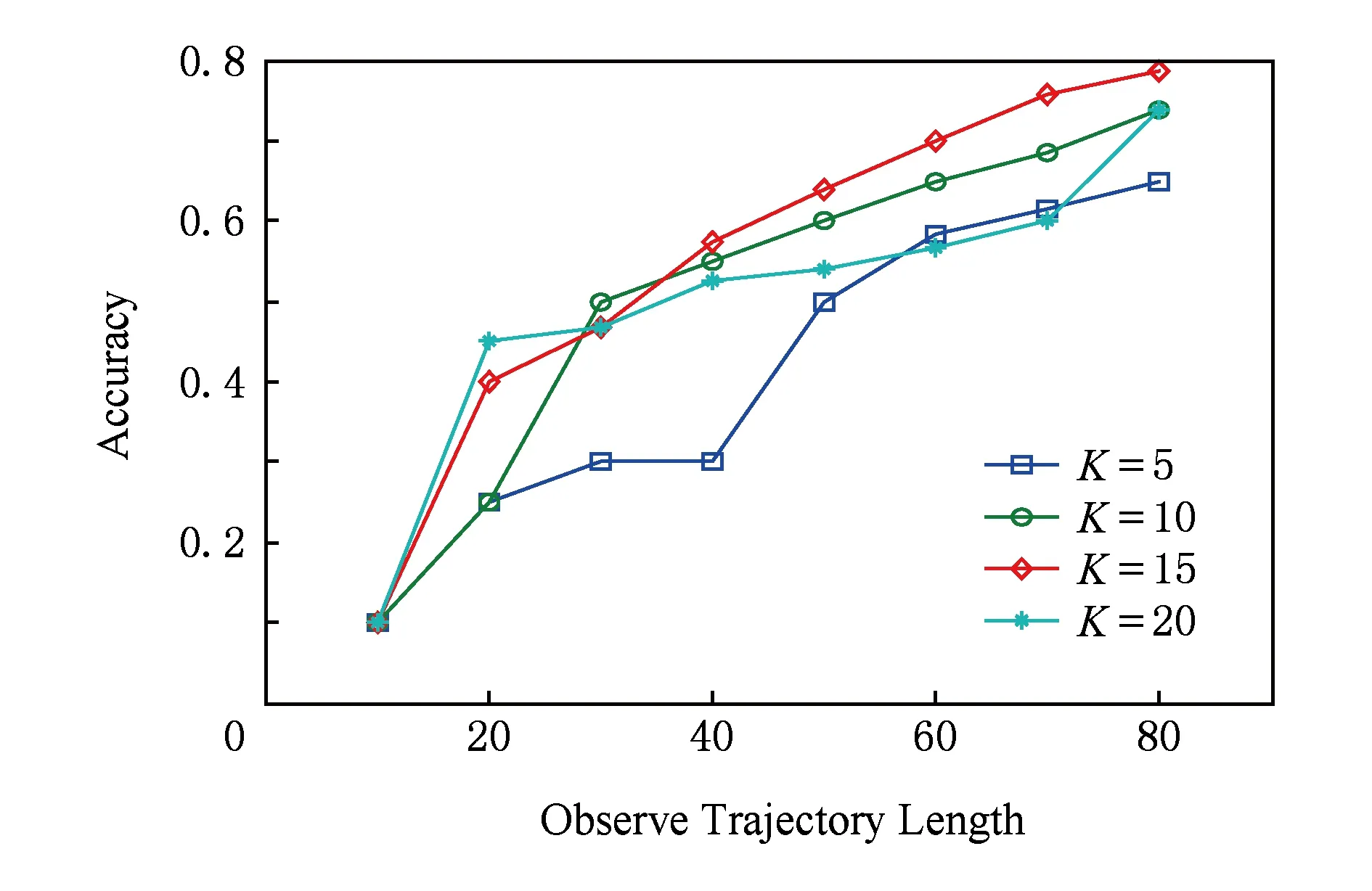
Fig. 5 Accuracy comparison of different observable length of input trajectories图5 不同输入历史轨迹长度下准确性比较

如图5所示，在相同的观察轨迹长度下，当高斯混合元组个数K从5增加到15，预测准确性明显提高，但当K进一步增加，预测精度开始下降，这表明高斯混合分量个数为15时，预测模型的精度最好.从图6可以观察到，预测模型的预测可信度在轨迹长度length=10时，预测可信度不高都为10%，随着轨迹点数的增加预测可信度提高；同时在相同的轨迹长度的情况下，预测可信度随混合分量的个数K从5到15逐渐提高，然而Kgt;15之后预测可信度保持基本不变，从图6中可以看到K=15的曲线预测可信度最高，且最高接近80%.混合分量过少时，预测模型不能将所有的运动模型包括在内，导致预测结果差，然而混合分量的个数也不宜过多，混合分量过多会导致模型建立时间增加，甚至可能引起高的时空训练代价.鉴于这些因素，在接下来的实验中统一设置高斯混合元组个数K=15.

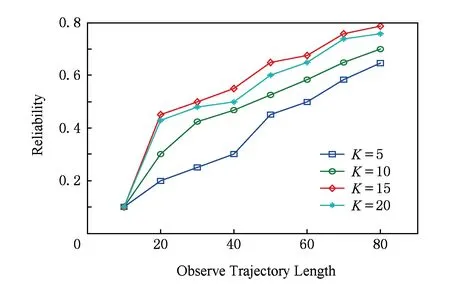
Fig. 6 Reliability comparison of different observable length of input trajectories图6 不同输入历史轨迹长度下预测可信度比较

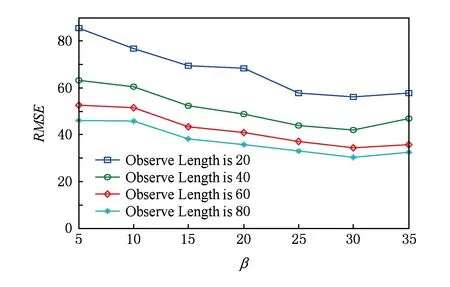
Fig. 7 Prediction error under different size of trajectory segment图7 不同轨迹段大小下预测误差比较

接下来考虑不同轨迹段大小β(K=15)的情况下进行轨迹预测，研究其是如何影响预测模型的性能.如图7所示，预测误差随轨迹段大小β增大而下降，然而在β=30之后略有上升，这是因为轨迹段大小增大，轨迹段可能包含了不满足轨迹段划分条件的轨迹点，因此预测误差增加.从图8～10可以了解到，预测准确性、预测可信度和平均精度随着β的增加而提高，但是在轨迹段大小β=30之后开始下降,这表明轨迹段大小β应该大到能够放下足够多的轨迹以至于包含足够多的运动模式，然而β太大而不能发现隐藏的轨迹模式，导致预测精度不高.

Fig. 8 Accuracy with different size of trajectory segment图8 不同轨迹段大小准确性比较

Fig. 9 Reliability under different size of trajectory segment图9 不同轨迹段大小预测可靠性比较

Fig.10 Average precision with different size of trajectory segment图10 不同轨迹段大小平均精度比较

4.3与已有预测模型或方法的比较

Fig. 11 Effect of randomly changing environment to prediction error, prediction reliability, and accuracy图11 环境变化对预测误差、预测可信度和准确性的影响

接下来比较本文所提预测算法(VGMM-ESATP)与基于高斯混合模型轨迹预测算法(Gaussian mixture model trajectory prediction, GMTP)[21]和基于Markov模型轨迹预测算法(Markov model trajectory predic-tion, MTP)[14].GMTP预测方法是一种利用高斯混合模型对轨迹数据建模，然后根据轨迹概率分布进行轨迹预测；MTP预测方法是借鉴Markov链无后效性的思想，计算移动对象状态转移概率，建立转移概率矩阵，并根据当前的转移概率与已有的转移概率矩阵对比进行轨迹预测.本文所提方法与GMTP预测算法的不同之处是本文使用VBEM算法进行模型参数估计和参数自适应选择算法灵活调整参数组合，该方法能够弥补GMTP方法参数估计出现过拟合或者局部最优的不足，而且还能改善GMTP方法在非高斯噪声中预测精度下降的问题.MTP预测算法与另外2种预测方法的差异除了模型不同之外，还缺少轨迹数据预处理操作，因此预测结果受噪声影响较大.本节仿真数据统一使用微软亚洲研究院Geolife项目的数据集，运用4.2节得到的参数高斯混合分量个数K=15和轨迹段大小β=30对模型性能进行比较评价.

1) 动态环境下预测结果分析.实际交通环境是随机变化的而不是恒定不变的，车辆的运动轨迹间隔也不是均匀的，在这种情况下采用传统高斯混合模型进行预测很难得到高精度的预测结果，因此我们提出基于变分高斯混合模型环境自适应轨迹预测方法，其能够自动调整高斯混合元组的个数以适应不同的环境.通过分析比较随机变化环境下以上所提3种算法的预测误差、预测可信度、准确性来证明所提方法的优势.设环境参考值n从4到-14动态变化，观察训练数据集大小对预测结果的影响.如图11所示,本文所提预测算法优于GMTP和MTP.从图11(a)可以看出ESATP预测方法平均预测误差均小于35 m，而GMTP预测算法的预测误差都在40 m以上，MTP的预测误差更是在50 m以上.这是因ESATP算法采用变分贝叶斯推理方法和参数自适应选择算法自动调整高斯混合元组个数，降低了模型对环境的敏感度.图11(b)表现了动态环境对预测算法的可信度的影响，ESATP的预测可信度均在90%以上;GMTP次之在83%以上;最差的是MTP算法，其可信度最高只达到83%.图11(c)随机变化环境对预测准确性的影响，ESATP预测准确率最高且稳定；GMTP虽然也很高，但波动比较大不稳定;MTP预测准确率最低，不超过30%.

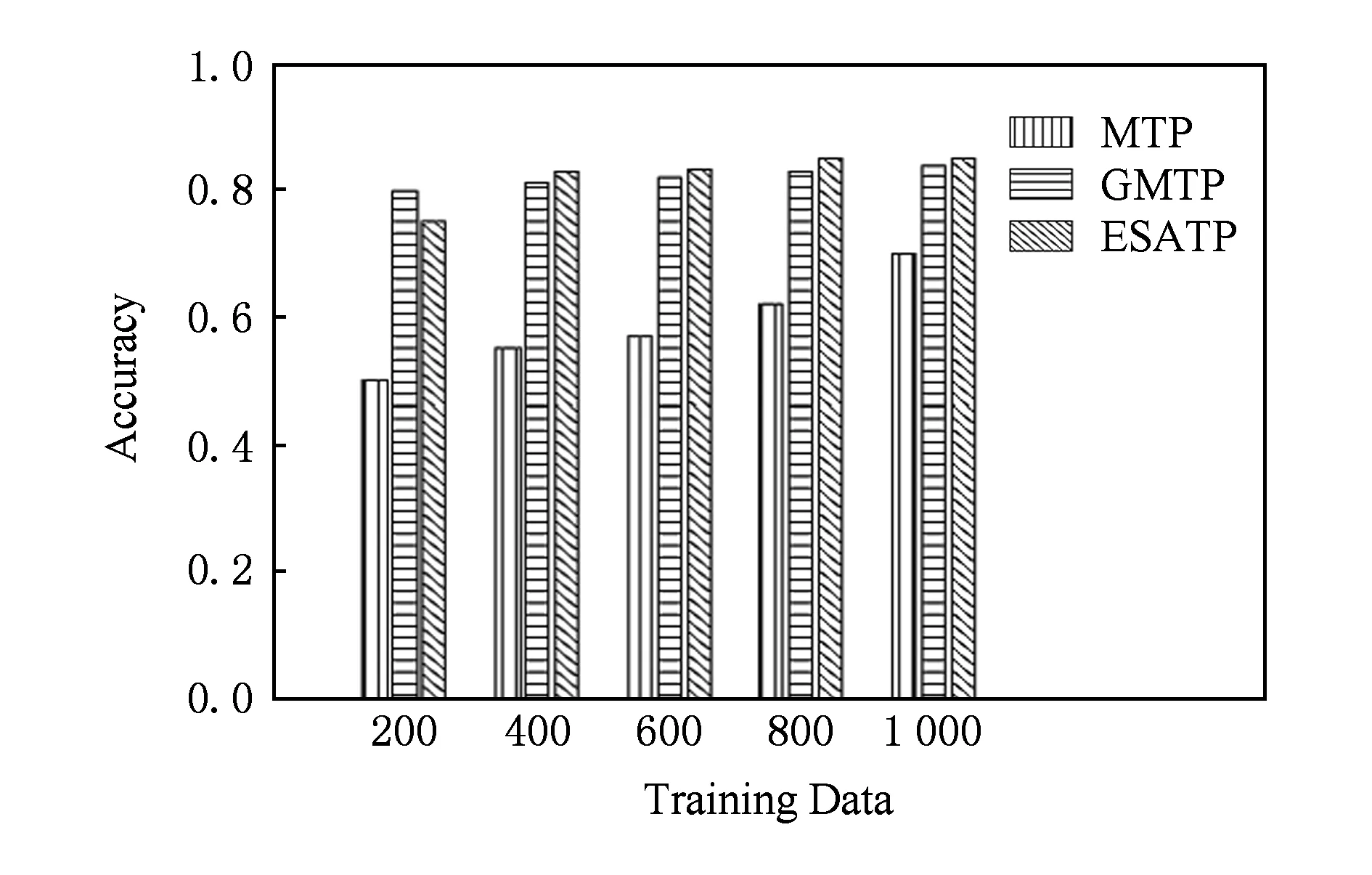
Fig. 12 Accuracy comparison in constant environment图12 恒定环境下预测准确性比较

2) 恒定环境下预测结果分析.比较恒定环境下ESATP，GMTP和MTP之间的预测准确率、预测误差和预测可信度.结果如图12～14所示.从图12和图14可以得出恒定环境下不同训练数据集ESATP和GMTP的预测准确率和预测可信度非常的接近，这是由于恒定环境下GMTP和ESATP算法中高斯混合模型分量个数只受训练数据集的影响，因此相同训练数据集GMTP与ESATP的预测准确率几乎相同.从图13可以看到恒定环境下ESATP，GMTP和MTP的预测误差.其中，ESATP的预测误差略优于GMTP；MTP的预测误差还是比较大，这是由于MTP没有对轨迹数据进行聚类处理，没有考虑轨迹间的相似性问题，因此预测误差比其他2种算法的预测误差都大.

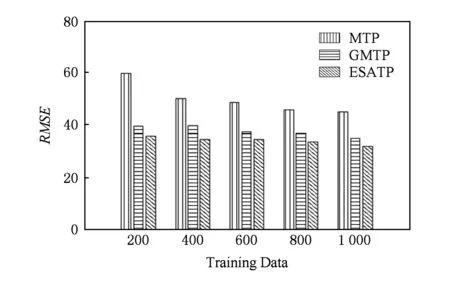
Fig.13 Error comparison in constant environment图13 恒定环境下预测误差比较

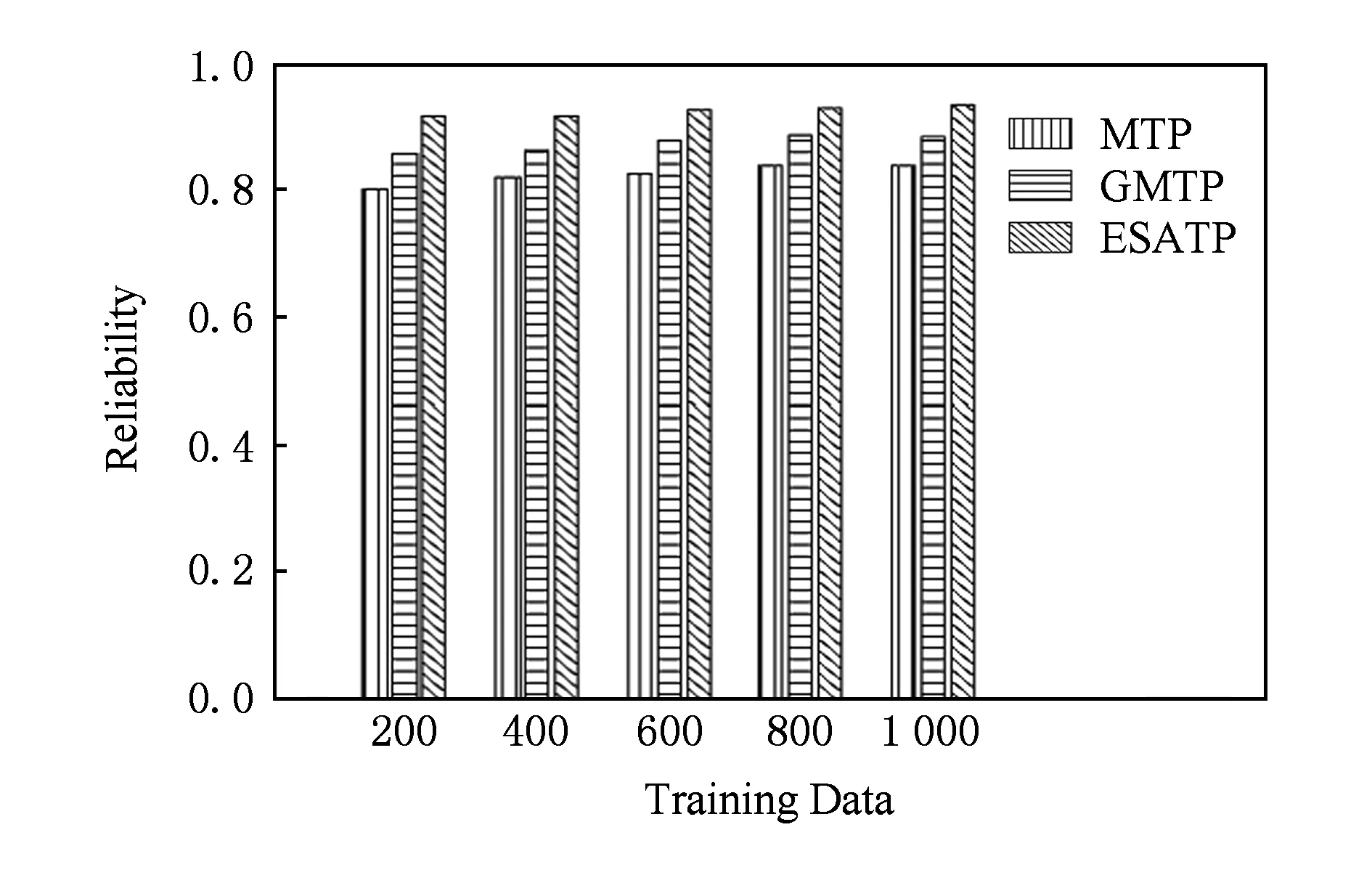
Fig. 14 Reliability comparison in constant environment图14 恒定环境下预测可信度比较

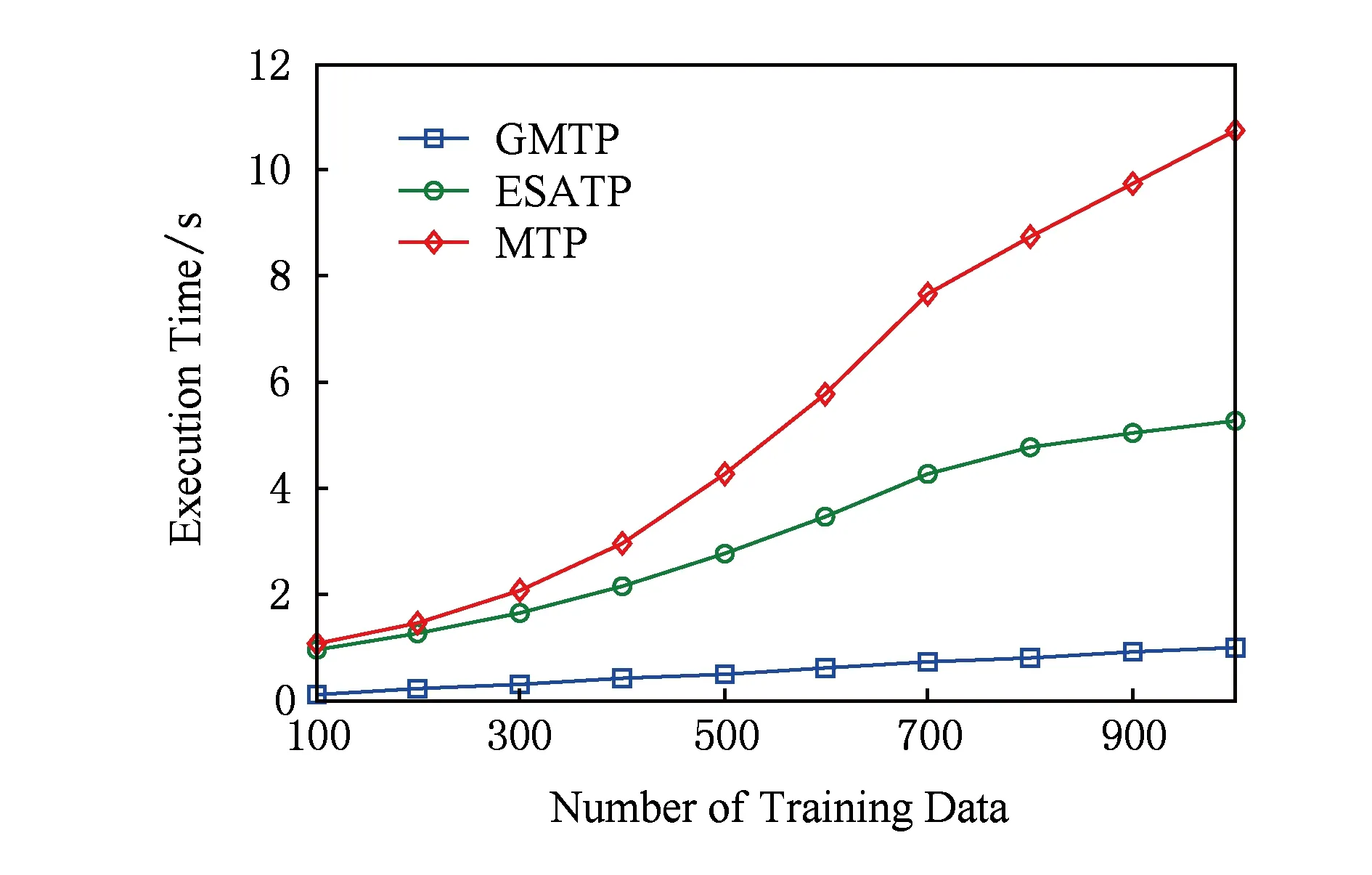
Fig .15 Prediction time comparison among typical trajectory prediction algorithms图15 典型轨迹预测算法时间性能比较

4.4预测时间比较

为了再进一步验证所提方法的性能，观察不同测试轨迹集的算法预测时间代价.图15中，ESATP的预测时间比GMTP的稍长，相比于MTP 算法要低得多.GMTP预测时间比ESATP小是因为ESATP方法中轨迹分段发现隐藏运动模式和参数自适应选择算法自动调整高斯混合元组个数以适应不断变化的环境过程中需要消耗较多的时间，因此，预测时间要比GMTP高一点.然而，EASTP比MTP算法的预测时间要少得多是因为EASTP利用高斯函数能够一次刻画多个轨迹点，因此要比MTP的预测时间小.

5 总 结

本文针对动态环境下很难对目标运动轨迹进行准确地描述，且轨迹数据中存在非高斯噪声，提出基于变分高斯混合模型环境自适应轨迹预测方法.为了预测动态环境中移动对象轨迹位置，首先运用聚类方法和轨迹分割方法优化轨迹源数据；其次，通过变分贝叶斯推理-期望最大化算法估计预测模型参数，得到更优的模型参数，并结合参数自适应选择算法调整参数组合，使预测模型能够适应不同的环境.实验结果表示所提的预测方法在保持较低的时间开销的同时预测精度较高.

在未来的研究工作中，除了考虑环境等客观影响因素之外，还将考虑驾驶员个人驾驶习惯和偏好主观影响因素对轨迹预测准确率的影响，进一步提高预测精度.

[1]Wang Zuchao, Lu Min, Yuan Xiaoru. Visual traffic jam analysis based on trajectory data[J]. IEEE Trans on Visualization and Computer Graphics, 2013, 19(2): 2159-2168

[2]Song Chaoming, Qu Zehui, Blumm N, et al. Limits of predictability in human mobility[J]. America Association for the Advancement of Science, 2010, 327(5968): 1018-1021

[3]Trasarti R, Guidotti R, Monreale A, et al. Myway: Location prediction via mobility profiling[J]. Information Systems, 2015, 64: 350-367

[4]Horvitz E, Krumm J. Some help on the way: Opportunistic routing under uncertainty[C]Proc of the 2012 ACM Conf on Ubiquitous Computting. New York: ACM, 2012: 371-380

[5]Xu Lingwei, Wu Chunlei, Wang Jingjin. A performance analysis of vehicle-to-vehicle communication system in the Internet of vehicle[J]. Netinfo Security, 2014 (7): 61-64 (in Chinese)(徐凌伟, 吴春雷, 王景景. 车联网中车-车通信系统性能分析[J]. 信息网络安全, 2014 (7): 61-64)

[6]Deb S, Jia C, Fong S. On-road directional trajectory prediction by junction-based pattern mining from GPS data[C]Proc of Int Conf on Machine Intelligent and Research Advancement. Piscataway, NJ: IEEE, 2013: 253-257

[7]Chen Ling, Lü Mingqi, Ye Qian, et al. A personal route prediction system based on trajectory data mining [J]. Information Sciences, 2011,11(35): 1264-1284

[8]Ying J C, Lee W C, Weng T C, et al. Semantic trajectory mining for location prediction[C]Proc of the 19th ACM SIGSPATIAL Int Conf on Advances in Geographic Information Systems. New York: ACM, 2011: 34-43

[9]Qiao Shaojie, Han Nan, Zhu W, et al. Traplan: An effective three-in-one trajectory-prediction model in transportation networks [J]. IEEE Trans on Intelligent Transportation Systems, 2014,16(3): 1188-1198

[10]Guo Chao, Li Kun, Wang Yongyan, et al. A location index for range query in real-time location system [J].Journal of Computer Research and Development, 2011, 48(10): 1908-1917 (in Chinese)(郭超, 李坤, 王永炎, 等. 面向实时定位系统的位置区域索引[J]. 计算机研究与发展, 2011, 48(10): 1908-1917)

[11]Schreier M, Willert Volker, Adamy J. Bayesian, maneuver-based, long-term trajectory prediction and criticality assessment for driver assistance system[C]Proc of IEEE Int Conf on Intelligent Transportation System. Piscataway, NJ: IEEE, 2014: 334-341

[12]Qiao Shaojie, Tang Changjie, Jin Huidong, et al. PutModel: Prediction of uncertain trajectories in moving objects databases[J]. Applied Intelligence, 2010, 33(3): 370-386

[13]Li Wen, Xia Shixiong, Liu Feng, et al. Location prediction algorithm based on movement tendency [J]. Journal of Communications, 2014, 2(35): 46-62 (in Chinese)(李雯, 夏士雄, 刘峰, 等. 基于运动趋势的移动对象位置预测[J]. 通信学报, 2014, 2(35): 46-62)

[14]Ziebart B D, Maas A L, Dey A K, et al. Navigate like a cabbie: Probabilistic reasoning from observed context-aware behavior[C]Proc of the 10th Int Conf on Ubiquitous computing. New York: ACM, 2008: 322-331

[15]Guo Limin, Ding Zhiming, Hu Zelin, et al. Uncertain path prediction of moving objects on road networks[J]. Journal of Computer Research and Development, 2010, 47(1): 104-112 (in Chinese)(郭黎敏, 丁治明, 胡泽林, 等. 基于路网的不确定性轨迹预测[J]. 计算机研究与发展, 2010, 47(1): 104-112)

[16]Qiao Shaojie, Shen Dayong, Wang Xiaoteng, et al. A self-adaptive parameter selection trajectory prediction approach via hidden Markov models[J]. IEEE Trans on Intelligent Transportation System, 2015, 16(1): 284-296

[17]Qiao Shaojie, Li Tianrui, Han Nan, et al. Self-adaptive trajectory prediction model for moving objects in big data environment [J]. Journal of Software, 2015, 26(11): 2869-2883 (in Chinese)(乔少杰, 李天瑞, 韩楠, 等. 大数据环境下移动对象自适应轨迹预测模型[J]. 软件学报, 2015, 26(11): 2869-2883)

[18]Lü Mingqi, Chen Ling, Chen Gencai. Position prediction based on adaptive multi-order Markov model [J]. Journal of Computer Research and Development, 2010, 47(10): 1764-1770 (in Chinese)(吕明琪, 陈岭, 陈根才. 基于自适应多阶Markov模型的位置预测[J]. 计算机研究与发展, 2010, 47(10): 1764-1770)

[19]Chen Meng, Yu Xiaohui, Liu Yang. Mining moving patterns for prediction next location [J]. Information Systems, 2015, 54(C):156-168

[20]Heravi E J, Khanmohammadi S. Long term trajectory prediction of moving objects using Gaussian process[C]Proc of the 1st IEEE 2011 Int Conf on Robot, Vision and Signal Processsing. Piscataway, NJ: IEEE, 2011: 228-232

[21]Wiest J, Höffken M, Kreßel U, et al. Probabilistic trajectory prediction with Gaussian mixture models [C]Proc of Intelligent Vehicles Symp. Piscataway, NJ: IEEE, 2012, 5(3): 141-146

[22]Qiao Shaojie, Jin Kun, Han Nan, et al. GMTP: A trajectory prediction algorithm based on Gaussian mixture model [J]. Journal of Software, 2015, 26(5):1048-1063 (in Chinese)(乔少杰, 金琨, 韩楠, 等. GMTP: 基于高斯混合模型的轨迹预测算法[J]. 软件学报, 2015, 26(5): 1048-1063)

[23]Huang C C, Manh H N, Hwang T H. Vehicle trajectory prediction across non-overlapping camera networks[C]Proc of IEEE Int Conf on Connected Vehicles and Expo. Piscataway, NJ: IEEE, 2013: 375-380

[24]Lei P R, Shen T J, Peng W C, et al. Exploring spatial-temporal trajectory model for location prediction [C]Proc of the 12th IEEE Int Conf on Mobile Data Management. Piscataway, NJ: IEEE, 2011: 58-67

[25]Birant D, Kut A. ST-DBSCAN: An algorithm for clustering spatial-temporal data[J]. Data amp; Knowledge Engineering, 2007, 60(1): 208-221

[26]Chan A, Li F W B. Utilizing massive spatiotemporal sample for efficient and accurate trajectory prediction[J]. IEEE Trans on Mobile Computing, 2013,12(12): 2346-2359

[27]Xu Dingjie, Shen Chen, Shen Feng. Variational Bayesian learning for parameter estimation of mixture of Gaussian [J]. Journal of Shanghai Jiao Tong University, 2013, 47(7): 1120-1125 (in Chinese)(徐定杰, 沈忱, 沈锋. 混合高斯分布的变分贝叶斯学习参数估计[J].上海交通大学学报, 2013, 47(7): 1120-1125)

[28]Mishra H K, Sekhar C C. Variational Gaussian mixture models for speech emotion recognition[C]Proc of the 7th IEEE Int Conf on Advances in Pattern Recognition. Piscataway, NJ: IEEE, 2009: 183-232

[29]Nasios N, Bors A G. Variational learning for Gaussian mixture models [J]. IEEE Trans on System Man and Cybernetics—Part B: Cybernetics, 2006, 36(4): 849-862

[30]Zheng Yu, Xie Xing, Ma Weiming. GeoLife: A collaborative social networking service among user, location and trajectory [J]. Bulletin of the Technical Committee on Data Engineering, 2010, 33(2): 32-39

[31]Ye M, Shou D, Lee W C, et al. On the semantic annotation of place in location-based social networks[C]Proc of the 17th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2011: 520-528

XiaZhuoqun, born in 1977. PhD. Associate professor at Changsha University of Science and Technology. His main research interests include wireless networks, VANET, smart grid.

HuZhenzhen, born in 1988. Master candidate at Changsha University of Science and Technology. Her main research interest is intelligence transportation system.

LuoJunpeng, born in 1992. Master candidate at Changsha University of Science and Technology. His main research interest is intelligent transportation.

AdaptiveTrajectoryPredictionforMovingObjectsinUncertainEnvironment

Xia Zhuoqun1,2,3, Hu Zhenzhen1,2, Luo Junpeng1,2, and Chen Yueyue3

1(Hunan Provincial Key Laboratory of Intelligent Processing of Big Data on Transportation (Changsha University of Science and Technology), Changsha 410114)2(School of Computer and Communication Engineering, Changsha University of Science and Technology, Changsha 410114)3(College of Computer, National University of Defense Technology, Changsha 410114)

The existing methods for trajectory prediction are difficult to describe the trajectory of moving objects in complex and uncertain environment accurately. In order to solve this problem, this paper proposes an self-adaptive trajectory prediction method for moving objects based on variation Gaussian mixture model (VGMM) in dynamic environment (ESATP). Firstly, based on the traditional mixture Gaussian model, we use the approximate variational Bayesian inference method to process the mixture Gaussian distribution in model training procedure. Secondly, variational Bayesian expectation maximization iterative is used to learn the model parameters and prior information is used to get a more precise prediction model. This algorithm can take a priory information. Finally, for the input trajectories, parameter adaptive selection algorithm is used automatically to adjust the combination of parameters, including the number of Gaussian mixture components and the length of segment. Experimental results perform that the ESATP method in the experiment shows high predictive accuracy, and maintains a high time efficiency. This model can be used in products of mobile vehicle positioning.

environment adaptive; variational Gaussian mixture model (VGMM); parameter adaptive selection algorithm; trajectory prediction

her bachelor and master degrees in computer science and technology from National University of Defense Technology (NUDT), Changsha in 2013 and 2015, respectively. PhD candidate in the College of Computer, NUDT. Her main research interests include mobile sensing and task assignment.

2017-05-08；

2017-08-10

国家自然科学基金项目(61572514)；湖南省自然科学基金项目(14JJ7043)；湖南省交通厅科技进步与创新项目(201405)

This work was supported by the National Natural Science Foundation of China (61572514), the Natural Science Foundation of Hunan Province of China (14JJ7043), and the Transportation Department Technological Progress and Innovation Fund of Hunan Province of China (201405).

胡珍珍(1102439691@qq.com)

(xiazhuoqun@sina.com)

TP391