DCuckoo：基于片内摘要的高性能散列表

蒋 捷 杨 仝，2 张梦瑜 代亚非 黄 亮 郑廉清

1(北京大学信息科学技术学院 北京 100871) 2(国防科学技术大学高性能计算协同创新中心 长沙 410073) 3(94782部队65分队 杭州 310021) 4(西京学院控制工程系 西安 710123)

(jiangjiecs@pku.edu.cn)

DCuckoo：基于片内摘要的高性能散列表

蒋 捷1杨 仝1，2张梦瑜1代亚非1黄 亮3郑廉清4

1(北京大学信息科学技术学院 北京 100871)2(国防科学技术大学高性能计算协同创新中心 长沙 410073)3(94782部队65分队 杭州 310021)4(西京学院控制工程系 西安 710123)

(jiangjiecs@pku.edu.cn)

散列表(Hash table)由于其支持高效的记录更新与检索操作，在计算机相关的各个领域中有着广泛的应用.但散列表有2个明显的缺点：冲突和低效的内存利用.最小完美散列使用N个位置存储N条记录，解决了冲突和空间效率的问题，但该算法不支持增量的更新.目标是设计一种高效的散列表，能够支持高速查询、最坏情况可以保证的高速更新、高效的空间使用以及动态的容量改变.结合 Cuckoo 散列和 d-left 散列的实现，提出了一个新的散列表设计方案——DCuckoo.DCuckoo 使用多级子表并应用了 Cuckoo 散列中移动已有元素的机制以提高装载率，且只保留了最末级子表的指针以减少空间浪费.为了进一步优化查询性能，DCuckoo 在片内内存中使用指纹和位图作为摘要，在查询时先匹配指纹，以减少对片外内存的访问次数.对 DCuckoo 进行了一系列实验，与其他5种散列表进行比较，发现 DCuckoo 达到了设计目标，并且在各项指标上均好于已有的散列表设计.

散列表；检索；指纹；片内内存；键值存储

散列表(Hash table)是根据关键字直接访问元素存储位置的一种数据结构.由于散列表支持高效的查询和更新操作，所以被广泛应用于各个领域之中，如 IP 查找[1-4]、负载均衡[5-6]、键值存储系统(key value store)[7-8]等.散列函数在本质上是将元素从大的定义域映射到小的值域上的一种变换，因此多个元素被映射到同一个位置是不可避免的，在散列表中这种情况被称为冲突(collision).当冲突发生时，插入散列表的记录将被放到其他位置，这会影响散列表的插入查询效率以及内存利用效率.因此，散列表算法设计中需要考虑的一个重要因素就是如何减少冲突与解决冲突.

散列表的设计主要有4 个目标：

1) 高效的查询操作.查询操作主要是对元素键(key)的比较，由于这一操作涉及到的内存访问相对散列值的计算时间需要消耗更多的指令周期.因此，可以用访存次数作为查询性能评价的指标.

2) 高效的更新操作.在插入元素的过程中，需要检测待插入元素是否已经存在，因此也涉及元素键值的比较，同样可以用更新时访存次数的多少作为衡量标准.

3) 高效的空间利用率.很多散列表设计为了保证性能需要一些桶为空，这就造成一定的空间浪费.此外，指针的使用也会占据一定的空间.一个高效的散列表应当尽可能减少这些空间浪费，提高内存利用率.

4) 支持动态的容量改变.在很多应用中，插入散列表的元素规模是在不断变化的，因此散列表也需要动态地改变容量以避免空间浪费或性能下降，而改变容量操作的时间与空间代价希望尽可能的小.

目前针对散列表的设计已有大量的研究，但这些研究都存在着一些缺陷，尚未有研究能同时解决以上4个问题.开散列法使用链表解决冲突，但指针的引入造成了一定的空间浪费.闭散列法依照探测序列安放元素，但其插入操作可能会失败.Cuckoo散列[9]为每个元素提供2个候选位置，在插入过程中若发生冲突会移动已有元素的位置，但这一过程中可能需要移动大量的元素造成性能低下.而 d-left 散列[10]则通过为元素提供更多的候选位置提高装载率，其缺点在于查询时需要依次探测这些候选位置，即访存次数较多.完美散列[11]为给定的集合生成散列函数，避免了冲突的存在，但构造完美散列函数开销较大，所以并不适用于需要更新的散列表.

以 d-left 散列为代表的多选择(multi-choice)散列最大的问题就是其较多的访存次数.文献[12-14]借助片内内存(on-chip memory)高速访问的特点存储散列表的摘要信息.在查询散列表前首先查询摘要，获得“元素可能在哪个桶中”这一信息，再查询片外(off-chip)的散列表，从而减少了访存次数，加快了查询速度.这一类研究中多使用布隆过滤器(Bloom filter)[15]作为片内摘要，但其缺点在于布隆过滤器不支持删除操作.

本文结合Cuckoo散列、d-left散列以及片内摘要的思想，提出了一种新的散列表设计方案——DCuckoo.DCuckoo以d-left散列为基础，即使用d个子表，每个元素在每个子表中都有一个候选位置，并在这d个子表中运用Cuckoo散列移动元素的机制，从而实现较高的装载率；为了减少指针造成的空间浪费，只保留最后一级子表的指针并减小该子表的长度；同时在片内内存中使用指纹(fingerprint)和位图(bitmap)作为摘要信息以减少对片外数据的访问，在支持高效的查询操作的同时也支持了删除操作.

本文实现了DCuckoo算法对并对其进行了实验，并与其他5种散列表设计进行了比较，结果表明DCuckoo算法实现了引言第2段所述的前3个设计目标：查询平均查找长度约为1；更新平均查找长度最坏情况可控；装载率达到95%实现了高效的空间利用.而多级子表的结构天然支持动态容量的改变：只需要动态地改变子表数量而无需重构整个散列表.因此，DCuckoo实现了以上4个设计目标.

1 相关工作

1.1Cuckoo散列

Cuckoo散列[9]使用2个散列函数h1(x)和h2(x)，将元素映射到2个不同的位置，即每个元素有2个候选位置.Cuckoo散列的原理如下：插入某元素x时，若2个候选位置中至少有一个为空，则将元素直接插入；若2个位置都被其他元素占据，则任意选择一个元素将其“踢出”(kick)，并在此位置插入x，被踢走的元素y则需要去查看它的另一个候选位置，若该位置为空，则直接插入，否则继续将占据这个位置的元素踢走，将y插入，重复这一踢的过程直到所有的元素都被插入到表中，或者踢的次数达到一定的上限(如500次)，这也是该算法被命名为布谷鸟(Cuckoo)的原因.

通过这种方式，散列表中的元素位置不断被调整到合适的空位，因此可以实现较高的装载率(gt;95%)，且其查询十分简单：最多只需要探测2个位置.Cuckoo 散列的不足之处在于：1)更新低效且可能产生更新失败；2)尽管Cuckoo散列最坏情况只需要2次记录探测，但平均情况下也需要1.5次，而理想的查询访存次数应当为1，也即 Cuckoo 散列的平均查询性能较差.

1.2d-left散列

与Cuckoo散列不同，d-left散列[10]使用d个散列子表，而非一个完整的散列表，每一个子表都有一个与之对应的散列函数hi(x).所以任意元素在每一个子表中都有一个候选位置，且由于散列函数不同，元素在每个子表中的位置往往不同.因此当2个元素在某一个子表中冲突时，在很大概率下这2个元素不会在其他子表中冲突，因此d-left散列同样可以实现较高的装载率(gt;90%).该算法中每一个子表都是一个标准的链式散列表，用于解决多级子表不能处理的冲突.当插入一个元素x时，算法从左到右依次检查每一级子表，若hi(x)的位置为空，则将x直接插入到这个子表中；若所有的候选位置都被其他元素所占据，则选择一个链表长度最短(负载最小)的桶插入.而查询时，算法依然从左到右依次探测每一个候选位置，直到找到合适的元素.无论是在插入还是查询，算法总是从左到右依次探测各级子表，虽然这一策略导致各个子表的装载率并不相同，但由于元素总是优先被插入到最左边，所以实际上查询时从左到右的顺序可以减少所需记录探测的数量.

该算法通过多候选位置降低了冲突的概率，但缺点在于每次查询也需要探测多个候选位置，造成查询性能的低下.此外，d-left的每一个桶中都包含一个链表，而在实际的应用中这些指针往往为空缺，也需要占据一定的内存空间，造成了空间浪费.

1.3使用片内摘要的散列表

一般的散列表规模较大，只能存储在片外内存(off-chip memory)中，相对于散列值的计算，对内存的访问需要消耗更多的CPU指令周期.以d-left为代表的多选择散列通过多候选位置的方式提高了散列表的装载率，同时带来的问题是查询时对片外访问的需求增加.片内内存(on-chip memory)具有容量小、速度快的特点.由于容量小，片内内存并不能容纳完整的散列表，但可以存储散列表的摘要(summary)，为片外内存中散列表的搜索提供一些指引，如“元素可能在哪些位置出现”这一类信息.在查询一个元素时，首先检索片内内存的摘要[16]，获得候选查询位置的集合，再在片外内存的散列表中的检索集合中的每一个位置.

Song等人[14]首先在散列表中应用这一方法，他们提出了一种基于片内摘要的散列表FHT(fast Hash table).FHT包含一个链式散列表和k个散列函数，即每个元素在散列表中有k个位置，片内使用计数布隆过滤器(counting Bloom filter[17])作为摘要.FHT是用布隆过滤器的方式十分巧妙：在构造散列表的过程中，插入一个元素都需要在其每个候选位置插入一个该元素的副本，并将该元素插入到片内的布隆过滤器中；当所有元素插入完毕后，对每一个元素只保留计数布隆过滤器中最小计数器位置对应的副本，其他k-1个副本全部删除.这样在查询时，只需要检索最小计数器位置的元素即可.

Segmented 散列[12]使用d个子表，类似d-left散列，每个子表的长度相同.该算法在片内为每个子表构建了一个布隆过滤器，用来表示元素是否在某个子表中存在.向某子表插入一个元素时，也需要向该子表对应的布隆过滤器插入元素.在查询时，只检索布隆过滤器报告存在的子表即可.

Peacock散列[13]也使用布隆过滤器作为片内摘要，但Peacock中每个子表的长度不同，各级子表的长度呈等比数列的关系依次递减，第1级子表容量最大，作为主表.插入时从主表开始为元素寻找合适的位置，因此后面的子表主要是为了解决前面子表的冲突.这种设计方式使得大部分元素存储在主表之中(90%)，因此在片内不为主表设置布隆过滤器，每次检索都要检查主表，起到了节省片内空间的效果.

2 DCuckoo算法

受到Cuckoo散列、d-left散列以及片内摘要的启发，本文提出了一个新的散列表设计DCuckoo.为方便理解，本节将对DCuckoo分为3个版本进行介绍，每一个版本都改进了上一个版本的缺点，并在最后针对散列表容量的动态调整提出了解决方案.

2.1DCuckoo1——结合d-left和Cuckoo散列

与d-left类似，DCuckoo1使用d个散列子表，每一个子表大小相同，均为标准的链式散列，原理图如图1所示:

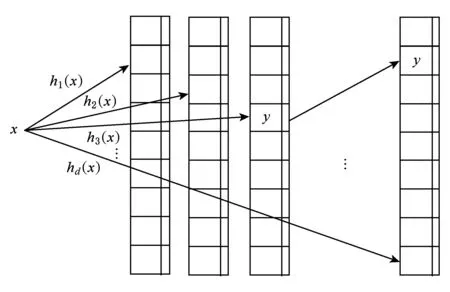
Fig. 1 DCuckoo1 structure图1 DCuckoo1原理图

当插入一个元素x时，DCuckoo1首先从左到右检查x在所有d个子表中的候选位置h1(x)，h2(x)，…，hd(x)是否有空位，如果有空位则直接插入，如果没有则进行一系列的“踢”操作——移动散列表中已有的元素，使所有的元素在散列表中找到合适的位置.DCuckoo中所采用的踢操作与Cuckoo散列类似，只是候选位置从2个变成了d个.插入元素x时，若x在d个候选位置中没有找到空位，首先查看其他元素是否可以通过一次移动找到合适的位置，若有则移动该元素，若没有则随机地从这d个候选位置中选出一个，用x将原先位于这个位置的元素y置换出，再对元素y进行插入操作.若在进行了θ次随机踢操作之后仍无法为元素找到合适的位置，则将目前未被插入的元素插入到对应候选位置的链表长度最短的链表中.

对DCuckoo1的查询与d-left相同，从左到右依次检查d个子表以及对应的链表，若找到匹配的元素则直接返回.

通过d-left多候选位置与Cuckoo散列移动元素机制的结合，DCuckoo1实现高装载率，同时避免了Cuckoo散列潜在的插入失败的问题.但DCuckoo1也继承了d-left的缺点：大量指针的使用造成空间浪费；查询时需要探测多个候选位置造成性能下降.这2个问题将分别在DCuckoo2和DCuckoo3中得到解决.

2.2DCuckoo2——减少指针的数量

如1.2节所述，存储指针需要消耗一定的内存空间，而实际上大部分指针都不会被使用到，但算法依然为存储指针预留了空间.因此，DCuckoo2只在最后一级子表中保留指针，并缩小该子表的长度，从而大幅度减少了指针的需求量.在插入元素时，若不能通过移动元素的方式为元素找到合适的空间，则将元素插入到最后一级子表的链表中.

2.3DCuckoo3——使用片内摘要优化查询和插入

DCuckoo3以指纹镜像作为摘要，而非用布隆过滤器.布隆过滤器的问题在于其不支持删除操作，虽然可以使用计数布隆过滤器解决这一问题，但这会增加复杂性.一个指纹对应由连续r位(bit)组成的一段内存空间，计算一个关键字的指纹时相当于对这个关键字进行了一次散列操作，将其映射到[0, 2r)这个空间中.因此指纹是对原关键字的一个摘要，它用很小的空间记录该关键字的信息.指纹可能会产生冲突，即一个指纹可能会对应多个关键字.DCuckoo3为片外的所有子表建立一个指纹镜像，即片外的每一个桶都对应片内一个指纹.在查询一个关键字时，先检查片内的指纹镜像中对应的指纹是否与该关键字的指纹相匹配，若匹配，再到片外的子表中去检索该关键字，从而大幅度减少了查询操作所需要的访存次数.由于指纹可能会产生冲突，指纹匹配并不一定代表片外对应位置的桶中存储着与该关键字匹配的元素，也即指纹的方式也具有一定的假阳性，与指纹的长度有关.

由于最后一级子表中可能存在着链表，而该子表中对应的指纹镜像只能提供位于桶中元素的信息，所以在查询时，如果在指纹报告元素存在的位置没有找到对应元素，则一定需要检查最后一级子表对应的链表，因为该链表的信息没有在摘要中表示.当查询操作所查询的元素不在散列表中时，这会造成大量额外的访存.对于这一问题，DCuckoo3针对最后一级子表对应的指纹镜像做一些额外的处理：这些指纹比标准的指纹多1位，用来表示片外子表中是否包含链表.在检索时，若这一位为0，则无需对链表进行额外的探测.

片内摘要也可以用来优化插入效率.在插入1个元素时，首先在片内摘要中查找该元素对应的d个位置是否都有指纹，若某位置无指纹意味着对应的片外桶中没有元素，可以直接插入.通过这种方式，插入元素所需的访存次数可以大幅减少.DCuckoo3最终原理图如图2所示：

Fig. 2 DCuckoo3 structure图2 DCuckoo3原理图

2.4子表动态调整

在很多应用中，需要插入到散列表中的元素集合可能会发生很大的变化，这时最开始的散列表可能就会显得过大或过小.处理这一问题最简单的方法是重建整个表，很多散列表使用这一方法进行重构，如Cuckoo散列、开散列散列表等.整体重构的处理方式缺点在于需要消耗大量的计算资源与内存空间，因为重构需要消耗大量的时间，而在这过程中系统应避免阻塞在重构过程中，所以重构的实现往往是在新的地址空间创建一个新的更大或更小的散列表，此时旧的散列表继续支持查询操作，当新表建立完毕后，再将旧表抛弃.得益于多级散列表的结构，在DCuckoo中可以很容易实现增加或者删除一个子表，避免因为链表长度过长或者装载率过高造成的潜在的性能下降问题.具体操作如下：当链表元素总数超过某一阈值或者整体散列表的装载率超过某一阈值时，增加一级散列子表，并将之前最后一级子表中链表上的元素进行重新插入操作；当散列表的整体装载率低于某一阈值时，为了避免空闲的桶造成的空间浪费，移除其中的某一级子表，并将该子表上的元素进行一次重新插入操作.因此DCuckoo可以很方便地支持散列表的重构操作.

3 实验结果与分析

实验中采用随机生成的数据集，数据关键字的长度为8B，值类型为32b整形(int)，插入数据集的规模为106个元素.查询数据集符合Zipf分布(在键值存储的实际应用场景中，查询请求大多符合Zipf分布[18])，规模为107个元素，Zipf分布偏度(skewness)为0.99，与数据库测试中经常使用的YCSB相同[19].

散列表设置方面，DCuckoo实现使用8级散列子表，最后一级子表的长度为普通子表长度的一半，指纹长度为15 b；在插入过程中如果发生冲突，只允许一次移动元素而不允许盲踢操作(θ=0).为了方便比较，本文另外实现了其他5种散列算法：开散列法(open hashing)、双散列法(double hashing)、Cuckoo散列、d-left散列、FHT，其中双散列和Cuckoo散列另外使用了一个大小与原始散列表大小相同的链式散列表用于解决冲突；为保证插入性能可控，双散列最大探测长度为16，Cuckoo散列踢操作上限为500次.d-left散列使用8级子表，FHT使用8个散列函数.实验结果表明DCuckoo在装载率、查询效率等方面均优于已有的散列表设计，具体结果如下所示.

3.1装载率

在这一实验中对所有的6种散列表使用相同的数据集，所有散列表大小均为插入数据集规模的1.05倍，即每个散列表包含1.05×106个桶，每插入10 000个元素后记录此时散列表的装载率，结果如图3所示.可以看到，DCuckoo、双散列法、Cuckoo都达到了非常理想的装载率，分别为95.17%，95.20%，95.18%，表明几乎所有的元素都在散列表中(满装载率约为100/105≈95.24%).但双散列法和Cuckoo散列都使用了额外的链式散列表用于解决冲突.装载率高意味着使用相同数量的桶可以容纳更多的元素，因此在插入相同数量元素的情况下，装载率高的散列表可以预先分配更少的片外内存空间.装载率随插入元素数量的变化如图3所示：

Fig. 3 Load factor with number of insertions图3 装载率随插入元素数量的变化

3.2查询平均访存

图4表示了将同样的元素插入到不同规模的散列表之后散列表的查询性能.横坐标代表散列表中桶的总数与插入元素数目的比值，纵坐标表示散列表构造完毕后一次查询所需的访存次数.可以看到DCuckoo在所有实验条件下都能达到接近1的平均查询访存次数，而其他散列表只有在散列表足够大的情况下才能达到这一水平.

Fig. 4 Average memory access with Hash table size图4 查询平均访存次数随散列表大小的变化

3.3插入平均访存

插入性能的实验过程同装载率测试，即在构建散列表的不同阶段进行测试，如图5所示.可以看到随着散列表逐渐变满，各个散列表的插入性能都有所下降，开散列法的插入访存相对稳定，这是因为在不考虑重复插入的情况，冲突发生时开散列法只需要将新建的元素放到散列表表头即可.DCuckoo在插入前9×105个元素时性能最优，尽管在最后有所下降，但扩充子表的方式可以保证最坏情况下可控.而Cuckoo散列由于最多可能执行500次踢操作，随着表中元素数目增多，插入性能会剧烈下降.插入平均访存次数随插入元素数量的变化如图5所示:

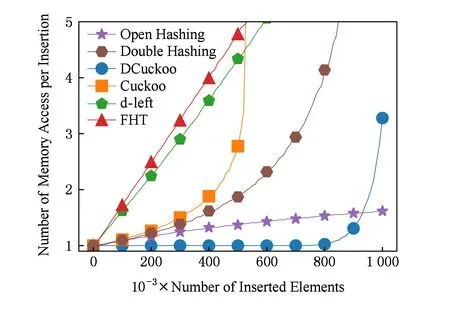
Fig. 5 Average memory access per insertion图5 插入平均访存次数的变化

3.4DCuckoo盲踢次数对冲突元素数目的影响

在3.1～3.3节的实验中，DCuckoo算法中不允许进行盲踢操作，若不能通过移动一个元素成功插入，则直接将元素插入到最后一级子表的链表之中.本文在不同的数据集下对盲踢次数与冲突元素数目之间的关系进行了实验，结果如表1所示：

Table 1 Number of Collision Items After θ Blind Kicks表1 θ次盲踢后冲突元素数目

从表1可以看到，当散列表大小为插入元素数目的1.05倍时，4次盲踢之内就可以几乎将所有的元素插入到散列表中，从而避免查询时对链表的访问带来的性能开销.

3.5不同数据集对查询性能的影响

本节的实验主要探究服从不同分布的查询数据集以及插入数据集的顺序对DCuckoo查询性能的影响.当DCuckoo不允许盲踢时，待插入元素若不能找到合适的位置，则会被直接放入链表，因此后插入的元素更有可能被放入到链表中.当查询数据集不是均匀分布时，插入的顺序可能会对查询性能产生影响，实验结果如表2所示.其中顺序插入(in order)指按查询数据集元素出现频数从高到低插入，逆序插入(reversed order)指按频数从低到高插入，乱序插入(out-of-order)即插入顺序与频数无关.

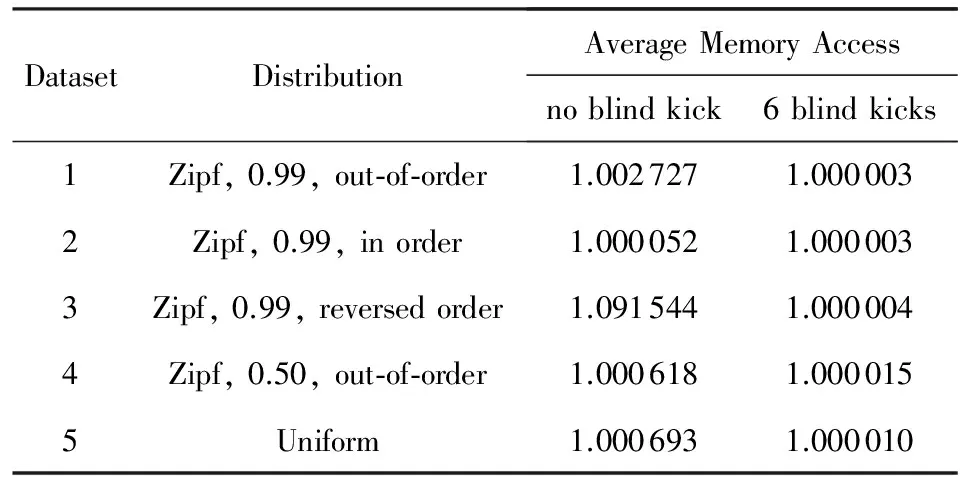
Table 2 The Results with Different Dataset for DCuckoo表2 DCuckoo在不同数据集下的实验结果

从表2可以看出，当不允许盲踢时，查询性能受插入顺序影响较大；而当允许盲踢6次时，平均查询访存则与插入顺序无关，且都达到了理想的水平(约1次).这是由于一方面盲踢减少了在链表上的元素数目，另一方面后插入元素不再直接插入链表，即链表上的元素与插入顺序无关.

这一实验结果表明的另一个问题是，出现在链表中的高频元素会影响查询性能，因此进一步的优化可牺牲一定的空间为元素标记“热度”，定期将“热度”较高的元素从链表中移出，以提高查询性能.

4 结束语

本文结合了Cuckoo散列和d-left散列，提出了一种新的散列表DCuckoo，并在其上应用片内摘要以优化查询插入性能.经过一系列的实验发现DCuckoo达到了设计目标，即高效更新、高效查询、内存冗余少、支持动态扩展，并优于已有的散列表设计.

未来的工作我们希望能够将DCuckoo应用到实际的系统之中，如键值存储系统.尽管对键值存储系统的研究已有很多，且也有基于CPU-GPU异构平台上的研究[8,20-22]，但这些研究都只对作为核心的散列表进行了很小的改动.因此，可以对现有键值存储系统的散列表进行替换，以追求更高的空间利用率以及查询性能.

[1]Broder A, Mitzenmacher M. Using multiple Hash functions to improve IP lookups[C]Proc of IEEE INFOCOM 2001. Piscataway, NJ: IEEE, 2001: 1454-1463

[2]Yang Tong, Xie Gaogang, Sun Xianda, et al. Towards practical use of Bloom filter based IP lookup in operational network[C]Proc of 2014 IEEE Network Operations and Management Symp (NOMS). Piscataway, NJ: IEEE, 2014: 1-4

[3]Yang Tong, Xie Gaogang, Li Yanbiao, et al. Guarantee IP lookup performance with FIB explosion[J]. ACM SIGCOMM Computer Communication Review, 2015, 44(4): 39-50

[4]Waldvogel M, Varghese G, Turner J, et al. Scalable High Speed IP Routing Lookups[M]. New York: ACM, 1997

[5]Adler M, Chakrabarti S, Mitzenmacher M, et al. Parallel randomized load balancing[C]Proc of the 27th Annual ACM Symp on Theory of Computing. New York: ACM, 1995: 238-247

[6]Mitzenmacher M. The power of two choices in randomized load balancing[J]. IEEE Trans on Parallel and Distributed Systems, 2001, 12(10): 1094-1104

[7]Mitchell C, Geng Yifeng, Li Jinyang. Using one-sided RDMA reads to build a fast, CPU-efficient key-value store[C]Proc of USENIX ATC’13. Berkeley, CA: USENIX Association, 2013: 103-114

[8]Zhang Kai, Wang Kaibo, Yuan Yuan, et al. Mega-KV: A case for GPUs to maximize the throughput of in-memory key-value stores[J]. Proceedings of the VLDB Endowment, 2015, 8(11): 1226-1237

[9]Pagh R, Rodler F F. Cuckoo hashing[C]Proc of the 9th European Symp on Algorithms. Berlin: Springer, 2001: 121-133

[10]Vöcking B. How asymmetry helps load balancing[J]. Journal of the ACM, 2003, 50(4): 568-589

[11]Fredman M L, Komlós J, Szemerédi E. Storing a sparse table with 0 (1) worst case access time[J]. Journal of the ACM, 1984, 31(3): 538-544

[12]Kumar S, Crowley P. Segmented Hash: An efficient Hash table implementation for high performance networking subsystems[C]Proc of the 2005 ACM Symp on Architecture for Networking and Communications Systems. New York: ACM, 2005: 91-103

[13]Kumar S, Turner J, Crowley P. Peacock hashing: Deterministic and updatable hashing for high performance networking[C]Proc of IEEE INFOCOM 2008. Piscataway, NJ: IEEE, 2008: 101-105

[14]Song Haoyu, Dharmapurikar S, Turner J, et al. Fast Hash table lookup using extended Bloom filter: An aid to network processing[J]. ACM SIGCOMM Computer Communication Review, 2005, 35(4): 181-192

[15]Bloom B H. Spacetime trade-offs in Hash coding with allowable errors[J]. Communications of the ACM, 1970, 13(7): 422-426

[16]Yang Tong, Liu Alex Xiangyang, Shahzad M, et al. A shifting Bloom filter framework for set queries[J]. Proceedings of the VLDB Endowment, 2016, 9(5): 408-419

[17]Fan Li, Cao Pei, Almeida J, et al. Summary cache: A scalable wide-area Web cache sharing protocol[J]. IEEEACM Trans on Networking, 2000, 8(3): 281-293

[18]Atikoglu B, Xu Yuehai, Frachtenberg E, et al. Workload analysis of a large-scale key-value store[C]Proc of SIGMETRICS 2012. New York: ACM, 2012: 53-64

[19]Cooper B F, Silberstein A, Tam E, et al. Benchmarking cloud serving systems with YCSB[C]Proc of the 1st ACM Symp on Cloud Computing. New York: ACM, 2010: 143-154

[20]Deyannis D, Koromilas L, Vasiliadis G, et al. Flying memcache: Lessons learned from different acceleration strategies[C]Proc of Computer Architecture and High Performance Computing (SBAC-PAD). Piscataway, NJ: IEEE, 2014: 25-32

[21]Hetherington T H, Rogers T G, Hsu L, et al. Characterizing and evaluating a key-value store application on heterogeneous CPU-GPU systems[C]Proc of IEEE ISPASS 2012. Piscataway, NJ: IEEE, 2012: 88-98

[22]Hetherington T H, O’Connor M, Aamodt T M. MemcachedGPU: Scaling-up scale-out key-value stores[C]Proc of the 6th ACM Symp on Cloud Computing. New York: ACM, 2015: 43-57

JiangJie, born in 1994. Master candidate. Received his bachelor degree from Peking University in 2016. His main current research interests include Hash tables and KV stores.

YangTong, born in 1982. PhD. Research assistant at the School of Electronics Engineering and Computer Science, Peking University. Member of CCF. His main research interests include IP lookups, Bloom filters, sketches and KV stores.

ZhangMengyu, born in 1995. Master candidate. Received her bachelor degree from the University of International Business and Economics in 2017. Her main research interests include Hash tables.

DaiYafei, born in 1958. PhD. Professor at the School of Electronics Engineering and Computer Science, Peking University. Member of IEEE. Distinguished member of CCF. Her main research interests include networked and distributed systems, P2P computing, network storage, and online social networks.

ZhengLianqing, born in 1963. PhD. Professor at the Department of Control Engineering, Xijing University. His main research interests include computer application technologies.

DCuckoo:AnEfficientHashTablewithOn-ChipSummary

Jiang Jie1, Yang Tong1,2, Zhang Mengyu1, Dai Yafei1, Huang Liang3, and Zheng Lianqing4

1(School of Electronics Engineering and Computer Science, Peking University, Beijing 100871)2(Collaborative Innovation Center of High Performance Computing, National University of Defense Technology, Changsha 410073)3(Military 9478265, Hangzhou 310021)4(Department of Control Engineering, Xijing University, Xi’an 710123)

Hash tables are extensively used in many computer-related areas because of their efficiency in query and insertion operations. However, Hash tables have two disadvantages: collisions and memory inefficiency. To solve these two disadvantages, minimal perfect Hash table usesNlocations to storeNincoming elements. However, MPHT doesn’t support incremental updates. Therefore, in this paper, combining Cuckoo hashing and d-left hashing, we propose a novel Hash table architecture called DCuckoo, which ensures fast query speed, fast update speed in worst cases, efficient utilization of memory and dynamic capacity change. In DCuckoo, multiple sub-tables and Cuckoo hashing’s mechanism of transferring existing elements are used to improve the load factor. Pointers except for ones in the last sub-table are eliminated for less wasted space. Also, in order to optimize the query performance, fingerprints and bitmaps are used as a summary in on-chip memory to reduce off-chip memory accesses. The bucket will be probed only if the corresponding fingerprint is matched in on-chip memory. We conduct a series of experiments to compare the performance of DCuckoo and other five Hash table schemas. Results demonstrate that DCuckoo eliminates shortcomings of both Cuckoo hashing and d-left hashing, hence DCuckoo achieves the four design goals.

Hash table; lookup; fingerprint; on-chip memory; key-value store

his master degree from Information Science and Electronic Engineering Department of Zhejiang University in 2011. His main research interests include computer networks.

2016-11-02；

2017-02-21

国家自然科学基金项目(61232004, 61672061)；国家quot;九七三quot;重点基础研究发展计划基金项目(2014CB340400)；国家重点研发计划项目(2016YFB1000300)；中国科学院先导科技专项课题(XDA06040602)

This work was supported by the National Natural Science Foundation of China (61232004, 61672061), the National Basic Research Program of China (973 Program) (2014CB340400), the National Key Research and Development Program of China (2016YFB1000300), and the Strategy Leading Science and Technology Projects of Chinese Academy of Sciences (XDA06040602).

杨仝(yang.tong@pku.edu.cn)

TP391