高三数学“结构化”教学设计的策略——以高考圆锥曲线焦点弦长有关试题为例

□周如俊

（江苏省灌南中等专业学校，江苏灌南222500）

高三数学“结构化”教学设计的策略
——以高考圆锥曲线焦点弦长有关试题为例

□周如俊

（江苏省灌南中等专业学校，江苏灌南222500）

普通高中数学学科应该培养学生“数学抽象”“逻辑推理”“数学建模”“数学运算”“直观想象”“数据分析”六大核心素养.“结构化”教学设计是培养学生核心素养的重要路径，避免学生碎片式学习与解题，造成“只见树木不见森林”的学习误区.

数学；核心素养；结构化；教学设计；策略

教育部《普通高中数学课程标准》修订组组长王尚志教授在有关专题报告中提出，普通高中学生数学学习中应培养学生“六大”核心素养[1].那么在高三数学总复习教学中如何补齐与落实培养学生数学学科核心素养呢？

笔者认为“结构化”的教学设计是提升学生“六大核心素养”的重要路径.高三数学“结构化”教学设计，要基于学生学习视角，跳出教材知识“散点”式的编排框架，探究知识点（链）之间的横向联系和纵向结构，使学生形成解题的核心知识、核心思维与核心方法，促进学生认知结构的整体化、化归化、系统化.具体而言，即教师从数学知识体系“结构化”的特点和学生认知“结构化”的形成与发展规律出发，帮助学生在已有认知结构基础上，让知识链延长与知识面拓展，把握解题结构之“本质”，从而从整体上把握数学知识、方法和观念，进而有效地克服肢解数学知识和方法的现象.

下面以2017年全国新课标Ⅰ卷（理）第10题（以下简称“例题”）的解题为例，就高三数学“结构化”教学设计问题作分析.

题目：已知F为抛物线C：y2=4x的焦点，过F作两条互相垂直的直线l1，l2，直线l1与C交于A，B两点，直线l2与C交于D，E两点，则|AB|+|DE|的最小值为_____.

A.16B.14

C.12 D.10

与之类似的试题是2008年全国Ⅰ卷（理）第22题：设椭圆其相应于焦点F(2,0)的准线方程为x=4.

（Ⅰ）求椭圆C的方程；

（Ⅱ）已知过点F1(-2,0)、倾斜角为θ的直线交椭圆C于A,B两点，求证：

（Ⅲ）过点F1(-2,0)作两条互相垂直的直线分别交椭圆C于点A,B和D,E，求|AB|+| DE|的最小值.

一、纵向“融通”设计——让解题方法“串”起来

课前给予学生文献[2]-[8]内容，培养学生“数据分析”能力（主要包括：收集文献数据，整理文献，提取信息，构建模型对信息进行分析、推断，获得结论）.教学中从圆锥曲线弦长求解结构化视角，引导学生对例题进行“数学抽象”，启发学生“一题多解”，发散性追溯的知识学习生长点与延伸点，让数学学习方法“串”通起来.从而激发学生探究圆锥曲线弦长求解的知识点的纵横联系，有效洞察其发生与发展的过程，掌握其在知识链中的结构关系，串成整体的知识链.

【例题“数学抽象”】已知F为抛物线C：y2=2px的焦点，过F作两条互相垂直的直线l1，l2，直线 l1与C交于A，B两点，直线 l2与C交于D，E两点，试求| AB|+| DE|的最小值.

（一）方法1：韦达定理法

即（| AB|+| DE|）min=8p=16，故选择A.

点评：数学运算是其解题活动的基本形式.学生在明晰运算对象的基础上，通过韦达定理法求弦长解题结构化，依据运算法则解决数学问题（主要包括：理解运算对象，掌握运算法则，探究运算方向，选择运算方法，设计运算程序，求得运算结果等），在运算中实现“演绎推理”，促进学生养成程序化、结构化思考问题的习惯.

（二）方法2：判别式法

设直线的斜率为k，被圆锥曲线截得弦AB两端点坐标为（x1,y1）、（x2,y2），则对方法1进行拓展，则有：

点评：判别式法是在方法1基础上实施“逻辑推理”的解题结构化，在“逻辑推理”核心素养的形成过程中，学生探究焦点弦长求解的问题本质，建构焦点弦长求解的“结构化”知识框架，从而在解题分析中培养学生形成有论据、有条理、合乎逻辑的思维品质.

（三）方法3：定义法

过A，B两点分别向x轴作垂线AA1，BB1，A，B为垂足，则点 A的横坐标为+

11|FA|·cosθ，点B的横坐标为-| FB|·cosθ.

以下解法同方法1.

点评：定义法是利用图形结构化（几何直观和空间想象）感知试题的形态与结构变化理解和解决数学问题（主要包括：借助空间认识事物的位置关系、形态变化与运动规律；利用图形描述、分析数学问题；建立形与数的联系；构建数学问题的直观模型，探索解决问题的思路），培养学生“直观想象”核心素养，增强学生运用图形和空间想象思考问题的意识，提升数形结合的能力.

（四）方法4：（参数）方程法

以下解法同方法1.

（五）方法5：极坐标法

以圆锥曲线的焦点（椭圆的左焦点、双曲线的右焦点、抛物线的焦点）为极点，过极点引相应准线的垂线的反向延长线为极轴，则圆锥曲线的统一极坐标方程为ρ=其中e为离心率，p是焦点到相应准线的距离.

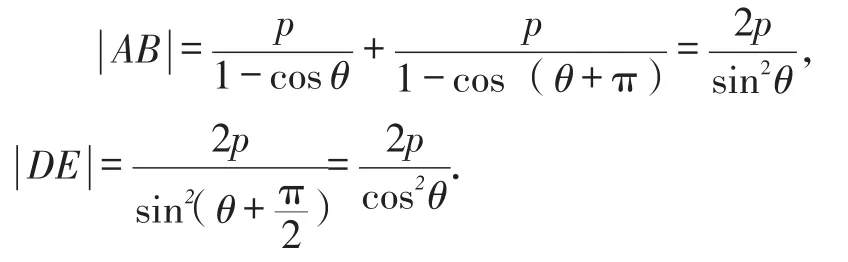
以下解法同方法1.

点评：（参数）方程法与极坐标法使学生解题结构化，培养数学建模的核心素养，即对试题进行抽象，用数学语言表达、用求弦长知识与方法构建极参数模型解决问题，提升学生数学应用能力，增强解题的创新意识.

二、横向“融通”设计——让数学思维“合”起来

圆锥曲线焦点弦长有关高考题内容，从题设上与有关文献[2]-[8]给出的公式看并不关联，且公式形态各异，但深入探究分析，就能发现它们内部隐藏的结构联系.引导学生依托“数据分析”与结论“化归”，探索解题本质、关联和规律，寻找它们之间的共性，将原本割裂的内容通过一条“结构化”暗线（万能公式）统“归”起来，实现焦点弦长求解的“结构化”.

（一）试题结构化“化归”

引导学生对例题作如下类型“化归”.

【例题“化归”类型】已知F为圆锥曲线C的焦点，过F作两条互相垂直的直线l1，l2，直线l1与C交于A，B两点，直线l2与C交于D，E两点，试分别求下列圆锥曲线C时（见表1）|AB|+| DE|的最小值.

表1

（二）解题结构化“转换”

基于上述6个题组，为了引导学生，给出一个通用定理.

【定理】已知点F和直线l是离心率为e的圆锥曲线C的焦点和对应准线，焦准距（焦点到对应准线的距离）为p.过F作两条互相垂直的直线l1，l2，直线l1与C交于A，B两点，直线l2与C交于D，E两点，且弦AB，DB均为焦点内分弦，则：

（2）| AB|+| DE|=

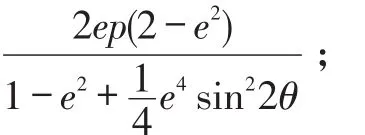
为了证明上述【定理】，引导学生对高中教材数学圆锥曲线方程作了拓展，进行数学建模与数据分析，通过圆锥曲线定义法推导，形成如下引理.

【引理】已知点F和直线l是离心率为e的圆锥曲线C的焦点和对应准线，焦准距（焦点到对应准线的距离）为p.过点F的弦AB与曲线C的焦点所在的轴的夹角为 θ(θ∈(0]［考虑到圆锥曲线关于通过焦点的对称轴对称，θ∈,π)时，θ用其补角（π-θ）代替］，则有焦半径|AF|=（ 内分 弦 ）、|AF|=（外分弦）；较短焦半径|BF|=（内分弦）、| BF|=（外分弦）；焦点弦的弦长| AB|=（内分弦）、| AB|=

利用【引理】易证明上述【定理】（证明内容略）.以下利用【定理】解答文章开头两道高考题.

【例题解析】令 e=1，则易得(| AB|+| DE|)min=8p，可快速口算出来答案：(| AB|+| DE|)min=8×2=16.

【2008年全国Ⅰ卷（理）第22题解析】

（3）由【定理】得：(| AB|+| DE|)min=

（三）考点结构化“拓展”

引导学生运用定理对上述圆锥曲线的标准方程（类型I-III共6种题组）进行解题结构化，形成多题“归一”结论：（| AB|+| DE|）min=

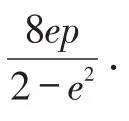
三、多向“融通”——让数学运用“连”起来

数学结构是有时奇妙、有时庞杂的系列题，犹如一张复杂的大网，笔者引导学生将上述考题结构“融通”，内容“结构化”，将数学知识进行多向相连、多维相整合，有关考点通向“四面八方”与“九九归一”.培养学生“逻辑推理”素养（归纳、类比、演绎）与数学抽象思维能力（从数量与数量关系、图形与图形关系中抽象出数学概念及概念之间的关系，从事物的具体背景中抽象出一般规律和结构，并且用数学符号或者数学术语予以表征），从而启发学生通过抽象、概括去认识、理解、把握圆锥曲线弦长的求解本质，由此学生建构的认知结构才能越牢固，越具连续性和发展性.

圆锥曲线焦点“弦长”问题历来是高考解析几何中的重要题型之一，由于此类问题形式多变、方法灵活，学生常常感到数学思想上难以澄清、解题方法上难以抉择.引导学生对圆锥曲线焦点弦“弦长”计算分析与推理，归纳出圆锥焦点弦长计算的万能公式：对此类问题的求解具有一定的规律性与简捷性.此公式解决了诸多文献[2]-[8]焦点弦长计算公式或因分类讨论、或因焦点位置不同等推出公式呈现形式不一、复杂难记的缺陷.

在此基础上，引导学生分析高考命题规律与解题策略：焦点弦长计算万能公式涉及四个参数：弦长| AB|、焦准距p、焦点弦所在直线倾斜角θ、离心率e，“知三求一”，达到“举一反三”析题效果.

（一）求焦点弦长（或焦半径）

【试题1】［2007年全国Ⅰ卷（理）第21小题］已知椭圆的左、右焦点分别为F1，F2．过F1的直线交椭圆于B，D两点，过F2的直线交椭圆于A，C两点，且AC⊥BD，垂足为P.

（Ⅰ）略；

（Ⅱ）求四边形ABCD的面积的最小值.（参考答案：最小值为）

【试题2】［2000年全国卷（理）第11小题］过抛物线y=ax2(a＞0)的焦点F作一直线交抛物线于P，Q两点，若PF与QF的长分别是p，q，则+等于（）（参考答案：C）

（二）求直线倾斜角θ（或斜率k）

【试题3】（2012年江苏卷第19题）如图1，在平面直角坐标系xOy中，椭圆的 左 、右 焦 点 分 别 为F1(-c，0)，F2(c，0).已知 (1，e)和都在椭圆上，其中e为椭圆的离心率.

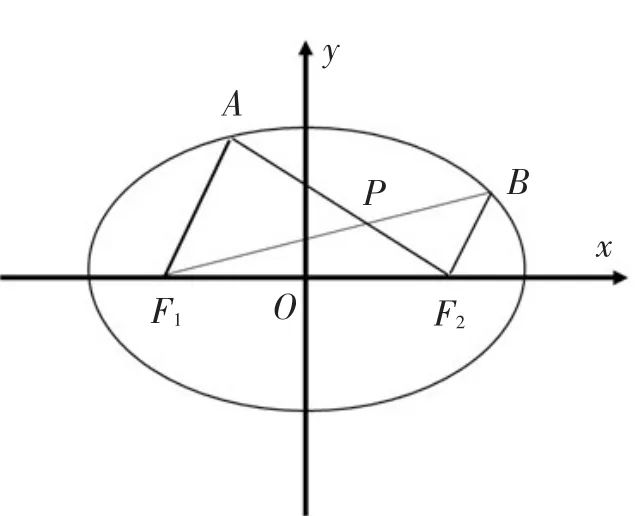
图1

（1）求椭圆的方程；

（2）设A，B是椭圆上位于x轴上方的两点，且直线 AF1与直线BF2平行，AF2与BF1交于点P.

1率；（参考答案：

（ii）略.

【试题5】［1983年全国卷（理）第10小题］已知椭圆长轴|A1A2|=6，焦距|F1F2|=4，过椭圆焦点F1作一直线，交椭圆于两点M，N，设∠F2F1M=α（0≤α＜π）.当α取什么值时，|MN|等于椭圆短轴的长？（参考答案

（三）求焦准距 p

【试题6】［2009年福建卷（理）第13题］过抛物线y2=2px(p＞0)的焦点F作倾斜角为45°的直线，交抛物线于A,B两点，若线段| |AB的长为8，则p=____.（参考答案：2）

【试题7】［2015年上海卷（理）第5题］抛物线y2=2px（p＞0）上的动点Q到焦点的距离的最小值为1，则p=_____.（参考答案：2）

（四）求离心率e

（2）略.

【试题9】［2010年全国Ⅰ卷（理）第16题］已知F是椭圆C的一个焦点，B是短轴的一个端点，线段BF的延长线交C于点D，且则C的离心率为_____（.参考答案：

［1］史宁中，林玉慈，陶剑，郭民.关于高中数学教育中的数学核心素养——史宁中教授访谈之七［J］.课程·教材·教法，2017（4）：8-14.

［2］罗荣建.椭圆双曲线焦点弦问题新解［J］.文山学院学报，2013（3）：37-41.

［3］马兴奎.圆锥曲线焦点弦问题探究［J］.数学通讯（上半月），2014（11/12）：22-24.

［4］王志红.圆锥曲线焦点弦长公式及其应用［J］.中学生数理化（学研版），2012（2）：46.

［5］彭世金.圆锥曲线焦点弦长的一个公式及其应用［J］.数学通讯，2007（22）：22-23.

［6］谢光亚.由两道高考解析几何试题谈圆锥曲线的统一性［J］.中国数学教育，2011（8）：28-29.

［7］方志平.椭圆、双曲线过焦点的弦长公式及其应用［J］.中学数学（高中版），2011（7）：49-51.

［8］倪铭宏.一道体焦半径拓展题的探究［J］.高中数学教与学，2016（12）：43-45.