圆锥曲线与直线相交的关联问题*——在章头图引领下对2017年全国高考Ⅰ卷（理）20题的探究

□翟洪亮

（江苏省太湖高级中学，江苏无锡214125）

圆锥曲线与直线相交的关联问题*
——在章头图引领下对2017年全国高考Ⅰ卷（理）20题的探究

□翟洪亮

（江苏省太湖高级中学，江苏无锡214125）

圆锥曲线中的定点、定值问题是高考中的重点题型，有些圆锥曲线的高考试题看似平常，实质超常，往往蕴含漂亮的性质，有较大的研究空间和教学价值.由章头图知圆锥曲线都是由平面去截圆锥的截口而得，故在一种圆锥曲线中具有的性质通常可以类比到其他类型的圆锥曲线去.

圆锥曲线；斜率；定点；定值；类比；章头图

圆锥曲线中的定点、定值问题是高考中的重点题型，高考试题是经过命题专家组精心命制而成的，有些试题看似平常，实质超常，往往蕴含漂亮的性质，有较大的研究空间和教学价值，需要我们去挖掘．由圆锥曲线与方程的章头图可知，圆锥曲线是由平面去截圆锥的截口而得，故在一种圆锥曲线中具有的性质通常可以类比推广到其他类型的圆锥曲线中去.在圆锥曲线与方程的章头图的引领下，现对2017年全国高考Ⅰ卷（理）中的一道解析几何题进行探究，与大家进行交流．

一、试题呈现

（1）求C的方程；

（2）设直线l不经过P2点且与C相交于A，B两点．若直线P2A与直线P2B的斜率之和为-1，证明：l过定点．

分析 作为一道高考试题，命题者独具匠心，要求考生从所给四点中进行选择，通过甄别，在对椭圆基本性质考查的同时，也进行对学生推理能力和运算能力的考查，试题短小精悍，给人留下清新飘逸的感觉，在解题时用点斜式直线方程求定值，首先要考虑斜率是否存在，具体解法如下.

参考解答（1）由于P3，P4两点关于y轴对称，故由题设知C经过P3，P4两点.

程为+y=1.

（2）当直线l的斜率存在时，设其直线方程为y=kx+m(m≠1)，与椭圆C方程联立得(1+4k2)x2+8kmx+4m2-4=0．

设 A(x1,y1)，B(x2,y2)，则即(2k+1)x1x2+(m-1)(x1+x2)=0，将 x1+x2=-代入得 m=-2k-1，此时 Δ=-64k，存在 k使Δ＞0成立．

所以l的方程为y=k(x-2)-1，过定点(2,-1)．

当直线l的斜率不存在时，设 A(s,t)，B(s,-t)，由直线P2A与直线P2B的斜率之和为-1，得=-1，解得 s=-2，此时l的方程为x=2，与椭圆C只有一个交点，不合题意，舍去．

综上可得，直线l过定点(2,-1)．

二、探究过程

对于此题，给出多余条件，让学生先排除再求解，这种命题风格自然想到2009年江苏省高考第14题：设{an}是公比为q的等比数列，|q|＞1，令 bn=an+1（n=1,2,…），若数列{bn}有连续四项在集合{- 53,-23,19,37,82}中，则6q= __．两者类似，如出一辙．直线P2A与直线P2B的斜率之和为-1，与直线l的斜率k的取值无关，故可以不考虑Δ＞0．此题条件简单，结论不一般！别解如下.

解：（1）P1(1,1)，P2(0,1)只能有一点在椭圆C上，同理只能有一点在椭圆C上，所以P1(1,1)一定不在椭圆C上．由P2(0,1)在椭圆C上得b=1，由在椭圆C上得a=2，所以椭圆C的方程为

（2）设直线l过定点D(x0,y0).当直线l的斜率存在时，设 A(x1,y1)，B(x2,y2)，直线 l2的 方 程 为y-y0=k(x-x0)，代入+y=1 ，得(4k2+1)x2+8k(y0-kx0)x+4(y0-kx0)2-4=0．故x1+x2=

又因为kP2A+kP2B=即(2k+1)x1x2+(y0-kx0-1)(x1+x2)=0，即(x02-2x0)k2+2(y0-1-x0y0)k+(y02-1)=0．

因为直线P2A与直线P2B的斜率之和为-1，与直线l的斜率 k的取值无关，所以

当直线l的斜率不存在时，同参考答案（略）．

综上可得，直线l过定点(2,-1)．

做完此题，笔者进行如下探究．

探究1若直线P2A与直线P2B的斜率之和为定值λ，直线l是否过定点？定值λ与定点的坐标之间存在什么关系？

解 设直线l过定点D(x0,y0)．当直线l的斜率存在时，设 A(x1,y1)，B(x2,y2)，直线l2的方程为y-y0=k(x-x0)，代入+y=1，得(4k2+1)x2+8k(y0-kx0)x+4(y0-kx0)2-4=0．故x1+x2=又因为kP2A+kP2B=即(2k-λ)x1x2+(y0-kx0-1)(x1+x2)=0，整理得(-λx2-2x)k2+(2y+2λxy-2)k+(λ-λy2)000000=0．

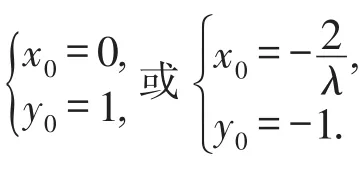
因为直线P2A与P2B的斜率之和为定值λ，与k的取值无关，故解得又直线l不经过P2点，所以直线l过定点(-,-1)．当直线l的斜率不存在时，设 A(s,t)，B(s,-t)，由已斜率之和为定值 λ，得得 s=-，当 -2＜-＜2时，即当λ＜-1或λ＞1时，直线l的方程为x=-，也过定点 (-,-1)．否则-1≤λ＜0 或0＜λ≤1，直线l与椭圆C不存在两个交点，不合题意，舍去．

由上可知，定点是在定直线y=-1上，直线P2A与直线P2B的斜率之和为定值λ是随着定点D(x0,y0)的横坐标的数值的变化而改变的，且定值λ=-．

结论1若直线P2A与直线P2B的斜率之和为定值λ（λ≠0），则直线l经过定直线y=-1上的定点(x,-1)，且λ=-．

能否将上述性质推广到一般情况？

证明：设直线l过定点D(x0,y0)．当直线l的斜率存在时，设 A(x1,y1)，B(x2,y2)，直线l的方程为 y-y0=k(x-x0)，代入b2x2+a2y2-a2b2=0，得 (a2k2+b2)x2+2a2k(y0-kx0)x+a2(y0-kx0)2-a2b2=0.故x1+x2=

因为直线PA与直线PB的斜率之和为λ，所以上式成立与k的取值无关，所以解得或又直线l不经过P点，所以直线l过定点

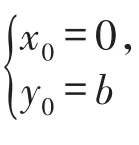
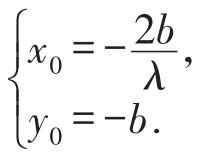
当直线l的斜率不存在时，设 A(s,t)，B(s,-t)，由已知斜率之和为定值 λ，得得当时，即当或时，l的方程为x=-，也过定点(-,-b)．否则 -≤λ＜0或0＜λ≤，直线l与椭圆C不存在两个交点，不合题意，舍去．

由于点P(0,b)是椭圆的上顶点，位置特殊，因此自然地联想到其他顶点时的情况，通过探究，同样可得：

（1）若点 P(0,-b)，则直线l经过定直线y=b上的点D(x0,b)，且

（2）若点 P(a,0)，则直线l经过定直线x=a上的定点D(a,y0)，且

（3）若点P(-a,0)，则直线l经过定直线x=-a上的定点D(-a,y0)，且

由圆锥曲线与方程的章头图和章头语可知，用一个垂直于圆锥的轴的平面去截圆锥，截口曲线是一个圆；用一个不垂直于圆锥的轴的平面去截圆锥，当截面与圆锥的轴夹角不同时，可以得到不同的截口曲线，它们分别是椭圆、双曲线、抛物线，我们通常把圆、椭圆、双曲线、抛物线统称为圆锥曲线．既然圆、椭圆、双曲线、抛物线都是由圆锥被平面所截，那么它们往往也具有类似的性质．椭圆中的上述性质在圆、双曲线、抛物线中是怎样的呢？

限于篇幅原因，以下探究过程省略．在圆C:x2+y2=r2中，通过探究可得如下结论：

结论4已知圆C:x2+y2=r2，设直线l不经过点P，且与C相交于A，B两点．若直线PA与直线PB的斜率之和为定值λ（λ≠0）．

（1）若点 P(0,r)，则直线l经过定直线y=-r上的定点D(x0,-r)，且

（2）若点P(0,-r)，则直线l经过定直线y=r上的定点D(x0,r)，且

（3）若点 P(r,0)，则直线 l经过定直线x=r上的定点D(r,y0)，且

（4）若点 P(-r,0)，则直线l经过定直线x=-r上的定点D(-r,y0)，且

（1）若点 P(a,0)，则直线l经过定直线x=a上的定点D(a,y0)，且

（2）若点 P(-a,0)，则直线 l过定直线x=-a上的点(-a,y0)，且

在抛物线y2=2px (p＞0)中通过探究，可得如下结论：

结论6已知抛物线y2=2px (p＞0)的顶点为P，设直线l与C相交于A，B两点．若直线OA与直线OB的斜率之和为定值λ（λ≠0），则直线l经过定直线x=0上的定点D(0,y0)，且

*本文系江苏省教育科学“十三五”规划课题“对高中数学教科书中章头图和章头语的教学研究”〔课题编号：B-b/2016/02/118〕的研究成果.