日常教学也要依“策”而行

卞正荣

一、利用线段图突破认知难点

与分数有关的教学内容，历来是小学数学教学中的难点，因为生活中用到分数、百分数的机会不多，学生对此缺少经验支撑，理解起来感到十分抽象。而图形的直观形象性恰好有助于弥补学生的这一认知缺陷，依靠画图策略帮助学生理解分数的意义，在学生应用分数知识解决问题的初始阶段往往可以起到事半功倍的效果。

如有关“一个数比另一个数多（或少）几分之几”的实际问题，在历次监测中的错误率很高，教材是在第二单元以“红花比黄花多”为例开始涉及这类问题的。在这一类问题中，没有直接说清楚“谁是谁的几分之几”，很多学生不知道应把谁看作单位“1”，难以正确分析数量关系，而采用数形结合的策略帮助学生正确理解题目中指的“谁是谁的几分之几”，则显得容易得多。请看教学片断：

师（出示例题及彩条图）：谁能在图上指一指，“红花比黄花多”意思是说哪一段是哪一段的？（学生照图选择后）谁能用语言表述一下，题目中指的谁是谁的 ？

生（边指边说）：“红花比黄花多”就是说红花比黄花多的是黄花的。

师：所以这里应该把什么看作单位“1”？

生：把黄花看作单位“1”。

师：求红花比黄花多多少朵，就是求什么？

生：求红花比黄花多多少朵，就是求50朵的是多少。

由于学生是第一次接触“一个数比另一个数多（或少）几分之几”这样的句子，为了使学生顺利理解其含义，教材给出了彩条图（本质上就是线段图），但由于学生是初次接触这类线段图，因此教师需要引导学生如何识图，在此基础上借助彩条图，学生完全可以自主探索出“红花比黄花多 ”是指多的朵数占黄花的。但本节课应该使学生在没有线段图示范的情况下也能理解类似句子的含义，教师要引导学生经历一个“根据线段图识图理解→自主画图理解→不用画图直接理解”的过程，因此接下来还应该教给学生画图的方法，当学生掌握了画图的方法后，他们在接下来的练习中遇到“小力的玻璃球比小军多”等句子时，就可以自己画图理解了，从而运用画图策略突破了教学难点；而当学生陆续进入到“不用画图直接理解”这一阶段时，他们的抽象思维能力也随之得到了发展。

二、利用线段图分析数量关系

很多分数应用题中涉及到的数量多，或者数量间的关系较为隐晦，给学生帶来了分析思考的难度，这时学生如果能恰当地应用画图策略，则分析解决问题时难度大大降低，如下面这道分数应用题：

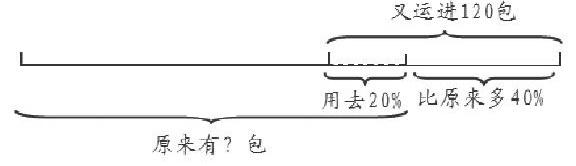
建筑工地有一批水泥，在用去了20%后，又运来了120包，这时的水泥数量比原来多40%。工地上原有是你多少包？

题中的几个量之间有什么关系？单从文字上看，应该是“原来的包数-用去的包数+又运来的包数=原来的包数+多出部分的包数”，根据这一相等关系列出的方程很复杂。而用线段图整理了题中的条件之后，数量间的关系则简明得多：

从图中可以看出，20%的部分和40%的部分加起来正好等于又运进的120包，从而可以列方程解答。

对于数量关系隐晦、复杂的应用题，学生一开始往往有无从下手之感，而当运用画图的策略以后，分析解答的正确率就会高很多，因为他们画图的过程，就是对条件进行整理的过程，同时由于线段图与文字相比更加直观，也有利于学生将隐藏的数量关系显性化。

三、利用线段图表达解答过程

应用题的解答过程讲究言必有据，一般每一步的解答结果都必须从条件开始一步一步地用算式表达出来，但由于受到学生知识水平、思维能力的限制，有些问题的解答结果从学生的角度还难以或不必用算式表达，如教材“鸡兔同笼”问题的解答方法中就有一种是画图解答，分数应用题的解答过程有时也可以借助线段图说明。如下题：

工人师傅加工一批零件，第一天加工了总个数的，第二天加工了剩下的，第二天正好加工了300个。这批零件一共有多少个？

这道题数量关系复杂，如果用常规解法步骤很多，属于“超纲题”，而如果学生运用画图策略的话，则可以化繁为简，轻易地把这道题目解答出来。从右图中可以看出，第二天加工的是剩下的，也就相当于总个数的，而第二天正好加工了300个，因此求总个数可以直接列式为“300÷”，对于的来历，如果学生不会列算式的话，也可以用线段图表示。

数学家希尔伯特在他的名著《直观几何》一书中谈到，图形可以帮助我们发现、描述研究的问题；可以帮助我们寻求解决问题的思路；可以帮助我们理解和记忆得到的结果。画图策略在数学学习中的作用无需多言，我们所要做的就是在日常教学中，创造条件让学生运用画图的策略，能画图时尽量画，使之产生依靠画图策略分析问题的意识，养成画图的习惯，提高识图、画图的能力。