基于链式法则的平面应变梯度的计算分析★

吕 娜 殷玉沉 孙玉周

(中原工学院建筑工程学院，河南 郑州 450007)

·结构·抗震·

基于链式法则的平面应变梯度的计算分析★

吕 娜 殷玉沉 孙玉周

(中原工学院建筑工程学院，河南 郑州 450007)

为了探究应变梯度的分布规律，建立新旧坐标系下平面矢量的坐标转换公式，应用链式法则，推导了新坐标系下应变梯度的变换关系式，分析并求解出了应变梯度的极值情况，为应变梯度传感器的使用提供理论依据。

应变梯度，链式法则，坐标转换，极值

1 概述

人类的现代化步伐离不开工程的现代化发展，无论是航空航天、地球海洋、冶金化工，还是地质岩矿、建筑结构、电力石油，每一类工程的实现都以工程力学为基础，从最初的设计到成品的安全监测，都离不开工程结构的力学分析。在土木工程领域中，应用最为广泛的材料是混凝土，混凝土作为一种混合材料，其内部骨料、水泥石上都含有一定的微裂纹或气泡，随着混凝土变形的发展，其内部微裂纹和气泡也相应发展、扩散直至贯通，形成宏观裂缝[1]。裂缝作为土木工程结构中最为常见的一种现象，不管是钢筋混凝土结构还是沥青混凝土结构或钢结构，在使用过程中都会有不同程度的裂缝出现。不同结构部位、不同宽度的裂缝对结构的承载能力、耐久性会产生不同程度的影响。

水泥混凝土的裂缝主要包括温度裂缝、材料自收缩裂缝以及外部荷载或结构变形作用下结构内力引起的裂缝。不管是何种裂缝，归根结底其产生的原因在于该处混凝土的拉应变超过了材料的极限拉应变，材料发生局部受拉破坏。结构在施工、使用过程中是否出现裂缝、在什么位置出现以及裂缝宽度的大小，是结构监测中迫切需要解决的问题。在结构损伤监测中，大多通过对应变进行测量和分析以确定混凝土中裂缝的产生和生长。现有的各类应变传感器测量应变时，均假设所测量区域内的应变为均匀分布，这显然有悖于损伤区域应变分布的真实情况。对混凝土类材料局部化破坏的研究表明，材料在发生破坏时，往往不会产生很明显的塑性屈服，而是由于内部微裂隙、微空洞等缺陷的扩展和连通使材料刚度降低，非线性变形积累，最终造成材料局部化损伤和破坏，在剪切带内部，常常发现有较大的应变梯度存在[2-6]。研究显示应变梯度相对于应变其变化更加剧烈，应变梯度显然更容易快速、直观地反映出损伤的位置，应变梯度信息对于结构健康监测具有不言而喻的重要价值[7]。通过对多峰反射光谱进行分析，有可能获得几毫米范围内的结构局部非均匀应变或应变梯度的变化情况，这一特性表明，光纤布拉格光栅的性能显著优于现有的用于结构损伤识别的其他各类应变传感元件[8]。为了探究应变梯度的分布规律，本文通过建立新旧坐标系下平面矢量的坐标转换公式，应用求导的链式法则，推导新坐标系下应变梯度的变换关系式。基于坐标转换推导出的任意方向上应变梯度表达式，分析讨论该状态下应变梯度的极大值、极小值及其对应方向，为应变梯度传感器的使用提供理论依据。

2 应变梯度的计算

在Oxy坐标系中，方向矢量r(x,y)经过变形为r′(x′,y′)，其平面应变分量为[9]：

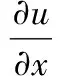
(1)

假设将坐标轴旋转α角(逆时针方向为正)，得到新坐标系Ox′y′，如图1所示。M点的位移矢量U在新坐标轴x′和y′上的投影为u′和v′，位移矢量U应与坐标系的选择无关，矢径也与坐标系的选择无关[10]，因此可得:

u′=ucosα+vsinα
v′=-usinα+vcosα
x=x′cosα-y′sinα
y=x′sinα+y′cosα

(2)

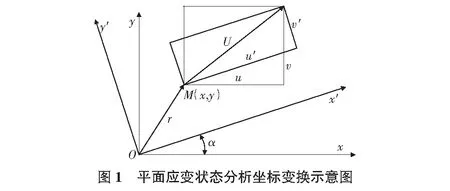
x=(x,y)表示原始参考构形，x′=(x′,y′)表示当前构形。从变形前到变形后的变形映射由x′=x′(x)定义，一阶变形梯度F和二阶变形梯度G分别为:

(3)

(4)

将式(1)代入式(3)可得:

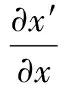
(5)

将式(1)代入式(4)，G111可表示为:

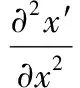
(6)

同理可得:

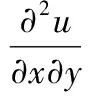
(7)

上式即为应变梯度表达式，则在新坐标系Ox′y′下应变梯度表示为:

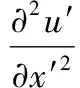
(8)

若把u′和v′看作是x和y的函数，x和y又是x′和y′的函数，由求导链式法则[11]，G111′可表示为:

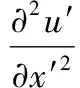
(9)

上式中的偏导数由式(2)求出为:

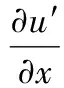
(10)

将式(6),式(7)和式(10)代入式(9)，整理后可得:

G111′=G111cos3α+G222sin3α+(G211+2G112)sinαcos2α+(2G212+G122)sin2αcosα

(11)

同理可得:

G112′=G112cos3α-G212sin3α+(-G111+G212+G122)sinαcos2α+(-G211-G112+G222)sin2αcosα

G122′=G122cos3α+G211sin3α+(-2G112+G222)sinαcos2α+(G111-2G212)sin2αcosα

G211′=G211cos3α-G122sin3α+(-G111+2G212)sinαcos2α+(-2G112+G222)sin2αcosα

G212′=G212cos3α+G112sin3α+(-G211-G112+G222)sinαcos2α+(G111-G212-G122)sin2αcosα

G222′=G222cos3α-G111sin3α+(-2G212-G122)sinαcos2α+(G211+2G112)sin2αcosα

(12)

上式即为坐标转换时应变梯度的转换规律，将G111′记为Gα，式(11)又可写成:

Gα=G111cos3α+G222sin3α+(G211+2G112)sinαcos2α+(2G212+G122)sin2αcosα

(13)

3 应变梯度的分析

式(13)表明，平面应变梯度Gα随α角的改变而变化，即Gα是α的函数，利用式(13)便可确定应变梯度的极值和它所在的角度。

式(13)对α求导可得:

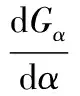
(14)

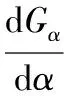
-3G111sinα0cos2α0+3G222sin2α0cosα0+(G211+2G112)(cos3α0-2sin2α0cosα0)+(2G212+G122)(2sinα0cos2α0-sin3α0)=0

(15)

方程式(15)的解α0即为应变梯度的极值位置，为了确定极值类型，将式(14)对α取导数，得:

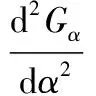
(16)

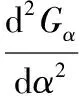
解方程式(15)如下，令α0≠Nπ，N为整数，方程两端同时除以cos3α0，可得:

-(2G212+G122)tan3α0-(2G211+4G112+3G222)tan2α0+2(2G212+G122-3G111)tanα0+(G211+2G112)=0

(17)

分别令a=-(2G212+G122)，b=-(2G211+4G112+3G222)，c=2(2G212+G122-3G111)，d=G211+2G112，a≠0代入方程可得:

atan3α0+btan2α0+ctanα0+d=0

(18)

由卡尔丹公式解方程式(18)可得:

(19)

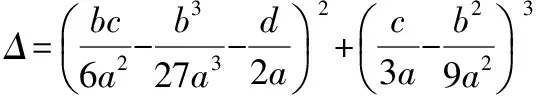
1)当Δ>0时，方程有一个实根和两个共轭复根，由于方程有工程实际背景，只取实根即tanα1。

2)当Δ=0时，方程有三个实根，此时有两种情况：

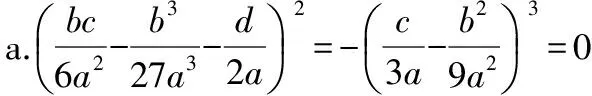
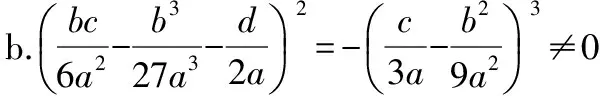
3)当Δ<0时，方程有三个不等的实根，即tanα1,tanα2,tanα3。

4 结语

通过对应变梯度状态的计算和分析，本文得出结论如下：

1)建立了新旧坐标系下平面矢量的坐标转换公式，应用求导的链式法则，推导了新坐标系下应变梯度的变换关系式；

2)分析了某变形状态的应变梯度G，得出了该状态下任意方向的应变梯度表达式；

3)分析了某变形状态的应变梯度G，讨论了该状态下应变梯度的极大值、极小值及其对应方向。

以上结论为光纤光栅应变梯度传感器的使用提供了理论依据。

[1] 陆 飞.分布式光纤传感技术在土木工程结构监测中的应用研究[D].南京：东南大学,2007.

[2] 赵吉东,周维垣,刘元高.岩石类材料应变梯度损伤模型研究及应用[J].水利学报,2002,33(7):70-74.

[3] 剡公瑞.岩石、混凝土类材料的断裂机理、模型研究及其工程应用[D].北京：清华大学,1994.

[4] 尚嘉兰,李廷芥.岩石细观损伤破坏的观测研究[J].实验力学,1999,14(3):373-383.

[5] Hill R,Hutchinson J W.Bifurcation phenomena in the plane tension test[J].Journal of the Mechanics & Physics of Solids,1975,23(45):239-264.

[6] Rudnicki J W,Rice J R.Conditions for the localization of deformation in pressure-sensitive dilatant materials[J].Journal of the Mechanics & Physics of Solids,1975,23(6):371-394.

[7] 鲍金秋,骆 英.一种基于应变梯度监测Ⅰ型裂纹的方法[J].力学与实践,2015,37(6):704-707.

[8] 郑世杰.结构健康监测:理论建模和计算智能方法[M].北京：国防工业出版社,2014.

[9] 徐秉业,刘信声.应用弹塑性力学[M].北京：清华大学出版社,1995.

[10] 刘鸿文.材料力学[M].第5版.北京：高等教育出版社,2011.

[11] 徐 信.用链式法则求复合函数的导数[J].中国远程教育,1983(1):6-9.

Calculationandanalysisofplanestraingradientbasedonchainrule★

LvNaYinYuchenSunYuzhou

(SchoolofCivilEngineeringandArchitecture,ZhongyuanUniversityofTechnology,Zhengzhou450007,China)

In order to explore the distribution law of strain gradient, the coordinate transformation formula of plane vector in new and old coordinate system is established. By using chain rule, the transformation relation of strain gradient in new coordinate system is deduced, and the extreme value of the strain gradient is analyzed and solved, which provides the theoretical basis for the application of strain gradient sensor.

strain gradient, chain rule, coordinate transformation, extreme value

1009-6825(2017)32-0021-03

2017-09-01 ★:国家自然科学基金(11472316)；河南省科技创新人才项目(164200510020)

吕 娜(1991- )，女，在读硕士； 殷玉沉(1990- )，男，在读硕士； 孙玉周(1974- )，男，博士，教授

TU311.4

A