带泊松跳随机延迟微分方程SST方法稳定性研究

贺 丹

(黑龙江工程学院 数学系，哈尔滨 150050)

带泊松跳随机延迟微分方程SST方法稳定性研究

贺 丹

(黑龙江工程学院 数学系，哈尔滨 150050)

近几年来，关于带泊松跳的随机微分方程，国内外文献仅限于显式或半隐式欧拉方法的研究，SST方法比显式或半隐式的欧拉方法具有更好的稳定性.针对几类带泊松跳的随机微分方程，研究了几类数值方法的稳定性.

微分方程；稳定性；延迟；数值方法

1 解析解的稳定性研究

本文中{Ω，F，{Ft}t≥0,P}是完备概率空间，{Ft}t≥0是其上满足正常条件(即右连续，包含所有的零测度集)的σ代数流，w(t)=(w1(t),w2(t),…,wl(t))T是定义在概率空间上的l-维布朗增量.

令N:Rd|→Rd,f:R+×Rd×Rd|→Rd及g:R+×Rd×Rd|→Rd×l是波莱尔可测函数，其中R+=[0,+∞). 本文分析的带泊松跳的随机延迟微分方程具有如下形式：

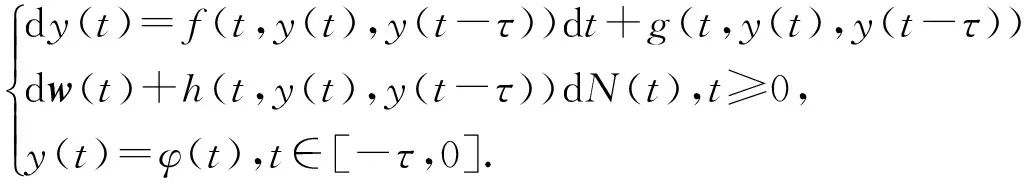
(1)

其中：τ是正常数，φ(t)是F0-可测得C([-τ,0];Rd)随机变量函数，满足下面条件

(2)

其中： E 表示关于概率P的数学期望.下面条件(a1)及(a2)是方程(1)解存在唯一性的充分条件：

(a1) (局部利普希兹条件) 存在常数KL>0及L>0，使得

|f(t,x1,y1)-f(t,x2,y2)|2∨|g(t,x1,y1)-g(t,x2,y2)|2∨|h(t,x1,y1)-h(t,x2,y2)|2≤KL(|x1-x2|2+|y1-y2|2),

(3)

对于所有|x1|∨|x2|∨|y1|∨|y2|≤L及t∈R+都成立.

(a2) (线性增长条件)

|f(t,x,y)|2|∨|g(t,x,y)|2|∨h(t,x,y)|2≤KG(1+|x|2+|y|2),

(4)

对于所有的(t,x,y)∈R+×R×R都成立，其中KG>0是常数.

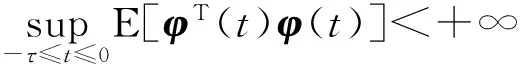
(5)

引理1 假设存在正定对称d×d矩阵Q及正常数μ1,μ2使得对于(t,x,y)∈R+×Rd×Rd，不等式

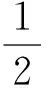
(6)

及-μ1+μ2<0成立，则方程(1) 是指数均方稳定的[1-3].

2 SST方法的稳定性研究

将SST方法用到方程(1)中，得到下面离散格式

(7)

(8)

(9)

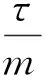
定义2 对于给定步长Δt，数值方法是指数均方稳定的如果存在正常数γ及C使得对于任意初始函数(t)，数值解yn满足下面不等式

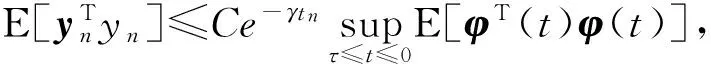
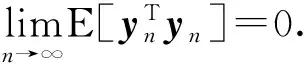
定理1 假设方程 (1) 满足条件 (6) 及-μ1+μ2<0，如果进一步假设存在常数K1、K2、K3及K4使得

fT(t,x,y)Qf(t,x,y)≤K1xTQx+K2yTQy,hT(t,x,y)Qh(t,x,y)≤K3xTQx+K4yTQy,(t,x,y)∈R+×Rd×Rd

(10)

则SST 方法在条件(7)～(9)下对于0∈(0,1),存在依赖于θ的常数的Δt，对于Δt∈(0,Δt0)，方法是渐近均方稳定的[4-5].

证明由式(9) 可以得到

(11)

由w(t)=(w1(t),w2(t),…,wl(t))T,标准l-维布朗增量，我们可得E(Δwi)=0，E[(Δwi)2]=Δt,E(ΔNi)=λΔt，E[(ΔNi)2]=λΔt(1+λΔt)及

对式(11)两端取期望得到下面不等式

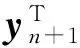
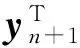
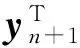
(12)

结合式(6)、(10)可得

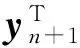
由式(8) 可以得到下面不等式

(14)

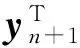
(15)

令

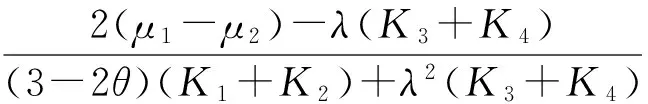
由于对于(0,1)，(3-2θ)>0则对于固定步长Δt(0,Δt0)，有下面不等式成立

2Δt(λ+λ2Δt)(K3+K4)+(3-2θ)Δt(K1+K2)-2(μ1-μ2))<0

因此可以得到下面不等式

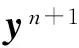
(16)

这就意味着当Δt∈(0,Δt)时，方法是渐近均方稳定的，定理证毕.

[1] IWANIEC T, MARTIN G. Quasiregular mappings in even dimensions [J]. Acta Math. 1993, 170(1): 29-81.

[2] HARDY G H, LITTLEWOOD J E. Some properties of conjugate functions [J]. J. Reine Angew. Math. 1932, 1932(167): 405-423.

[3] HARDY G H, LITTLEWOOD J E. Some properties of fractional integrals II [J]. Math. Z. 1932, 34: 403-439.

[4] 魏代俊, 郭 黎. 一类奇异双调和方程的特征值问题[J]. 鲁东大学学报:自然科学版, 2008, 24(2): 20-25.

[5] XING Y. Two-weight inequalities for some operators applied to harmonic forms [C]// Proceedings of the Conference on Differential & Difference Equations and Applications, Melbourne, 2006. 1159-1166.

MeansquarestabilityofSSTmethodforstochasticdelaydifferentialwithPoissonjump

HE Dan

(Department of Mathematics, Heilongjiang Institute of Technology, Harbin 150050, China)

Recently, the study of stochastic delay differential equations are all about the explicit Euler method or the semi-implicit Euler method, the SST method have better stability property than the explicit Euler method and the semi-implicit Euler method. This paper took some stochastic delay differential equations as example, studied the stability of SST method for these stochastic delay differential equations.

stochastic delay differential equations; stability; delay; numerical method

2017-01-05.

贺 丹(1980-)，女，硕士，研究方向：基础数学.

O175

A

1672-0946(2017)05-0619-02