常见雷达信号分选算法研究

张 德 交

(哈尔滨工程大学，哈尔滨 150001)

常见雷达信号分选算法研究

张 德 交

(哈尔滨工程大学，哈尔滨 150001)

在电子对抗中，信号往往复杂多变，对雷达信号的分选提出了新的要求.要准确地确定主辐射源，确定干扰手段，就要从一连串脉冲流中分选出来自同辐射源的脉冲序列.为了分选时域上不同特征的雷达信号——常规信号、抖动信号以及参差信号——先后对PRI变换法、改进了的PRI变换法以及SDIF法这三种分选算法进行了研究，并对这些算法在不同参数上分别用Matlab进行了仿真，实验表明PRI变换法能检测常规信号，但不能检测抖动雷达信号以及参差雷达信号的子周期；改进后的PRI变换法可以检测10%以内的抖动信号；而SDIF算法不仅能检测出常规信号和参差信号，而且运算量较小,达到了分选常见雷达信号的目的.

信号分选；PRI变换法；改进的PRI变换法；SDIF算法；Matlab 仿真

雷达信号分选在雷达侦查系统中的地位不容忽视.雷达信号分选是将无规则交叠的信号流中分离出各单个雷达信号的过程.其原理就是利用接受到的各种参数(脉冲到达角、载频、脉宽、幅度及到达时间等)，将交织混杂在一起的脉冲信号分出各雷达的单脉冲信号[1].

在雷达侦察干扰中，信号的分选技术越发关键.其中信号的脉间的时域特征包括参差 PRI、抖动 PRI、滑变 PRI等.而常见的分选方法有：PRI变换法、改进的PRI变换法、序列差值直方图法(SDIF法)等.本文将着重介绍上述几种常见的分选方法，以及通过对不同时域特征雷达信号分选的仿真，归纳出它们的适用条件[2-4].

1 PRI变换法

PRI变换法只考虑脉冲到达时间[5-6].设脉冲的到达时间为tn,n=0,1,2,……N-1，其中N为脉冲个数，这样到达的脉冲串为：

(1)

那么g(t)的自相关函数的表示如下：

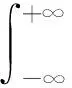
(2)

(3)

将式(1)带入式(2)、(3)得：

(4)

(5)

其中:τ>0，D(τ)为脉冲重复间隔的谱图.可以看到，上式是在自相关函数法上做复积分得到的.对交杂的脉冲信号进行自相关运算，会在PRI整数倍处出现峰值现象.而在PRI变换法中，潜在PRI处只有一个峰值，较理想地克服了子谐波的影响[7].

为了便于分析，对PRI变换进行离散化.设PRI的变化范围[τmin,τmax],将其分成K个相等小区间，每个小区间宽度为b=(τmax,τmin)/K.设第k个小区间的中心为：

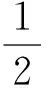
(6)

确定PRI的存在范围、PRI箱的中心值以后，Dk可以化简为：

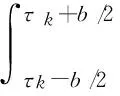
exp[2πjtn/(tn-tm)]

(7)

当b→0 时，Dk/b→D(τ).潜的PRI用|Dk|过门限值对应的脉冲间隔来表示，再按估计出的PRI值进行序列搜索[8].

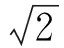
图1 PRI变换法分选3列固定周期脉冲信号

由仿真结果可以看出PRI变换法对高次谐波的抑制效果是明显的，结果很理想.而对脉冲流加入10%抖动时，仿真如图2所示.

图2 PRI变换法分选3列10%抖动脉冲信号

当抖动达到10%时，的峰值降低得并不明显，以致部分谐波分量出现，难以完全抑制，导致无法进行信号的分选.所以PRI变化法对于大抖动的脉冲信号检测不是很理想.而当输入脉冲流为一个子周期分别为0.22、0.58 ms，帧周期为1 ms的三参差雷达脉冲序列时，仿真结果如图3所示.

可以看出，PRI变换算法无法检测出参差脉冲序列，只可以检测出帧周期.所以PRI变化法在分选参差信号时，也会遇到困难.

图3 PRI变换法分选1列三参差脉冲信号

2 改进的PRI变换法

PRI变换法在处理PRI固定的常规脉冲序列时，能有效地抑制谐波.但是，对于 PRI抖动的脉冲列，该方法的分选效果并不理想.主要有两个原因：一是由于脉冲列的到达时间逐渐远离起始时间，相位因子的相位误差逐渐增大；二是本应集中在同一个小区间的脉冲对由于抖动的存在而被平均分布在PRI值附近的几个区间中.因此，针对以上两点，本文对 PRI 变换法进行了修正和改进[9].

针对相位因子逐渐增大的误差，可改变相对开始时间以达到减小的目的.从而改进相位因子 exp[2πjtn/(tn-tm)]，避免了相位误差带来的影响.

针对第二个原因，则可设置交叠的PRI小区间.设雷达脉冲的抖动量是ε，PRI小区间数是K，则第k个小区间的中心值为τK=(k-1/2)b+τmin,k=1,2,…,K[τmin,τmax]是 PRI 的估计范围，令重叠 PRI的箱宽为bk=2ετk.

改进的PRI变换法的具体算法流程如下：

1)初始化，令Dk=0,(1≤k≤K)，n=2；

2)令m=n-1；

3)令τ=tn-tm,若τ≤τmin(1-ε)，跳转到式(11)；否则τ≥τmax(1-ε)，跳转到式(12)；

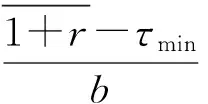
5)对每个k=k1，…进行式(6)～(10)；

6)初始化起始时间.当第k个PRI首次出现时，则令tok=tn；

7)初步计算相位并分解：η0=(tn-tok)/τk，v=round(0)，ζ=η0/v-1；

8)如果满足((v=1)&&(tn=tok))&&(|ζ|≤ζ0)，则更新起始时间：tn=tok；

9)重新计算相位η=(tn-tok)/τk=(tn-tok)/τk；

10)更新PRI变换值Dk=Dk+exp(2πjη)；

11)对m=m-1，如果m<1则转到式(12)，否则转到(3)；

12)对n=n+1，如果n>N,停止.否则转到式(2)[8].

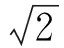
图4 改进的PRI变换法分选3列10%抖动脉冲信号

可以看出，在脉冲抖动为10%时，经改进后的PRI变换法，仍然能够明显地测出峰值，分选效果较理想.

3 SDIF算法

序列差值直方图法(SDIF)基本原理是：首先计算序列相邻脉冲的时间差，形成的第一级差值直方图，确定检测门限.如果有一个值超过门限，则将其对应的PRI进行脉冲序列搜索；否则不进行脉冲序列搜索，直接统计下一级的差值直方图，再搜索脉冲序列.将直接分离出的序列剔除，然后继续对剩余的脉冲序列从第一级统计的新差值，重复以上过程[8-10].

仿真及分析：输入一列三参差的周期雷达信号，脉冲重复周期PRI为111 μs，子PRI分别为11 μs和35 μs，脉宽为2.5 μs，观测时间为200 μs.仿真结果如图5所示.

图5 SDIF算法分选1列三参差脉冲信号

可以看出，SDIF法分选存在参差的单脉冲序列时，能够成功分离出所有的子PRI，分选效果理想.

如果输入一个三参差和一个常规的周期信号，三参差信号参数如上，常规信号的周期为181 μs，到达时间为1 μs，脉宽为2.5 μs，观测时间为200 μs，仿真结果如图6所示.

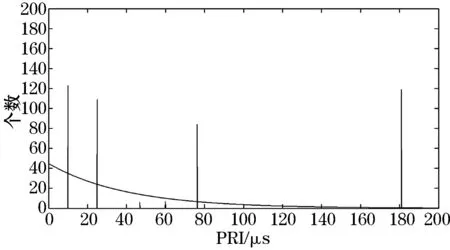
图6 SDIF算法分选1列三参差脉冲信号和1列常规信号

可以看出，SDIF法分选常规周期信号和参差信号时，能够成功分离出所有的子PRI和帧PRI，分选效果理想.

4 结 语

本文通过对PRI变换，改进的PRI变换，以及SDIF分选方法的研究及仿真，发现对常规的PRI脉冲序列进行分选时，效果较理想.但当PRI存在抖动时，由于TOA距时间起点较远，增大了相位误差，而且本来集中于同一个PRI区间的脉冲序列分散在以PRI为中心附近的几个PRI区间中，出现部分谐波分量导致真实的PRI可能淹没在噪声中.而

且PRI变换法无法检测参差脉冲序列，只能检测出帧周期，由此引入了修正的 PRI 变换法，该方法有效地改进 PRI 变换的缺点，并将成功分选信号的抖动范围提高到了10%.虽然在运算量上较大，但能够有效地抑制子谐波分量.而针对参差信号分选引入的SDIF算法不仅计算量少，而且能够有效地分选参差信号.

[1] 杨 多. 复杂环境下多参数雷达信号分选算法研究[D]. 哈尔滨: 哈尔滨工程大学, 2012.

[2] 乔宏乐, 王 超, 王 鹏. 基于PRI变换法的脉冲信号分选算法[J]. 火控雷达技术, 2012, 41(2): 34-38.

[3] 周 政, 唐 宏, 张永顺. 基于PRI的参差雷达脉冲列分选方法[J]. 现代防御技术, 2009, 37(5): 123-126.

[4] 李国君, 舒 洪, 赵栋华. 一种改进的动态关联信号分选算法[J]. 雷达科学与技术, 2011, 12(6): 547-550

[5] NISHIGUCHI K, KOBAYASHI M. Improved algorithm for estimating pulse repetition intervals [J]. IEEE Transactions on Aerospace and Electronic Systems, 2000, 36(2): 407-421.

[6] 王兴颖, 杨绍全. 基于脉冲重复间隔变换的脉冲重复间隔估计[J]. 西安电子科技大学学报, 2002, 29(3): 355-359.

[7] 栾 超. 雷达信号分选关键技术研究[D]. 哈尔滨: 哈尔滨工业大学, 2012: 34-41.

[8] 明 焱. 未知雷达信号PRI分选算法研究[D]. 西安: 西安电子科技大学, 2013, 21-22, 29-31, 38-42.

[9] 程 翔. 复杂电磁环境下雷达信号脉间分析算法研究[D]. 南京: 南京航空航天大学, 2011. 36-39.

[10] 赵观星. 雷达电磁环境模拟系统的设计与实现[D]. 南京: 南京理工大学, 2013. 34-37.

Researchonsortingalgorithmforcommonradarsignal

ZHANG De-jiao

(Harbin Engineering University, Harbin 150001, China)

In electronic countermeasure environment, signals are dense and complex, which are new challenges to radar signal sorting. For the purpose of leading the countermeasures system choose the main radiation source and determining the interference means promptly and accurately, pulse sequence derived from the same source of the radiation must be sorted from a series of staggered pulses exactly. In order to sort different characteristics of the radar signal on the time domain——normal signal, staggered PRI signal and dither signal, PRI transform algorithm, the improved PRI transform algorithm, and SDIF algorithm are studied in sequence and simulated with Matlab by different parameters. At last the application conditions, the advantages and disadvantages of each algorithm were analyzed. It showed that PRI transform algorithm can sort normal signal, but it cannot sort either signal or the child PRI of staggered PRI signal. The improved PRI transform algorithm could sort dither signal which dithered no more than 10%, and SDIF algorithm could not only sort normal signal and staggered PRI signal, but also has a easier computational work. The aim of sorting common radar signal has been achieved.

signal sorting; PRI transform algorithm; improved PRI transform algorithm; SDIF algorithm; Matlab simulation

2016-03-26.

张德交(1989-)，男，硕士，研究方向：雷达信号的分选.

TN957

A

1672-0946(2017)05-0577-04