Mises屈服条件下内边界自由环板受线性载荷作用下的极限载荷

张登霞,崔世堂,胡立明

(陆军炮兵防空兵学院， 合肥 230031)

【基础理论与应用研究】

Mises屈服条件下内边界自由环板受线性载荷作用下的极限载荷

张登霞,崔世堂,胡立明

(陆军炮兵防空兵学院， 合肥 230031)

应用Mises屈服条件得到了外边界简支和外边界固支两种边界条件下自由环板在线性载荷作用下极限载荷的理论计算结果。针对以上两种不同的边界条件，采用合适的试函数，采用加权残数法，给出了极限载荷的数值结果。与Tresca条件下的数值结果进行了比较，比较结果表明，计算结果是合理的。

加权残数法;Mises屈服条件； 极限载荷； 环板

环板是工程上常用的一种结构型式，在环板上的某一点进入屈服之后，仍然可以承受更大的载荷，直到达到塑性极限状态。因此，对于环板来说，为更好地发挥材料的性能，特别对塑性性能较好的材料，考虑塑性设计比弹性设计更为节省材料，更加合理。由此可见，找出环板塑性极限载荷具有重要的工程意义。

对于环板的塑性极限分析，一般采用最大Tresca屈服条件[1]，但对于铁、铜、铝、镍和软钢等材料，Mises屈服条件比Tresca屈服条件更接近实验结果与实际问题[3]，通常选用的最大弯矩极限条件和实际有较大差别[3]。由于Tresca屈服条件是线性的，而Mises屈服条件是非线性的，因此在塑性极限分析问题中采用Mises屈服条件将使计算复杂。目前，采用Mises屈服条件考虑环板的塑性极限问题，大都借助于加权残数法，得到一个简捷实用的极限荷载表达式。针对工程中环板常见的受载情况，吴向等[4]应用Mises屈服条件求出了3种支撑情况下环板受均布载荷作用的极限载荷，刘福林[5-6]应用Mises屈服条件求出了内边界简支外边界自由环板在线性载荷作用下的极限载荷。蒋朝志等[7]应用Mises屈服条件求出外边简支环板受均布载荷作用的极限载荷，但尚未见到对于外边界简(固)支、内边界自由环板在线性载荷作用下的分析结果。因此，本文针对理想刚塑性环板，应用Mises屈服条件，选用加权残数法建立了上述两种情况下的塑性极限求解式，以便工程应用。

1 外边界简支、内边界自由环板在线性载荷作用下的极限载荷

假设作用于内边界自由外边界简支环板的载荷分布情况如图1所以。环板的内外半径分别为b、a,载荷的最大极限为q。

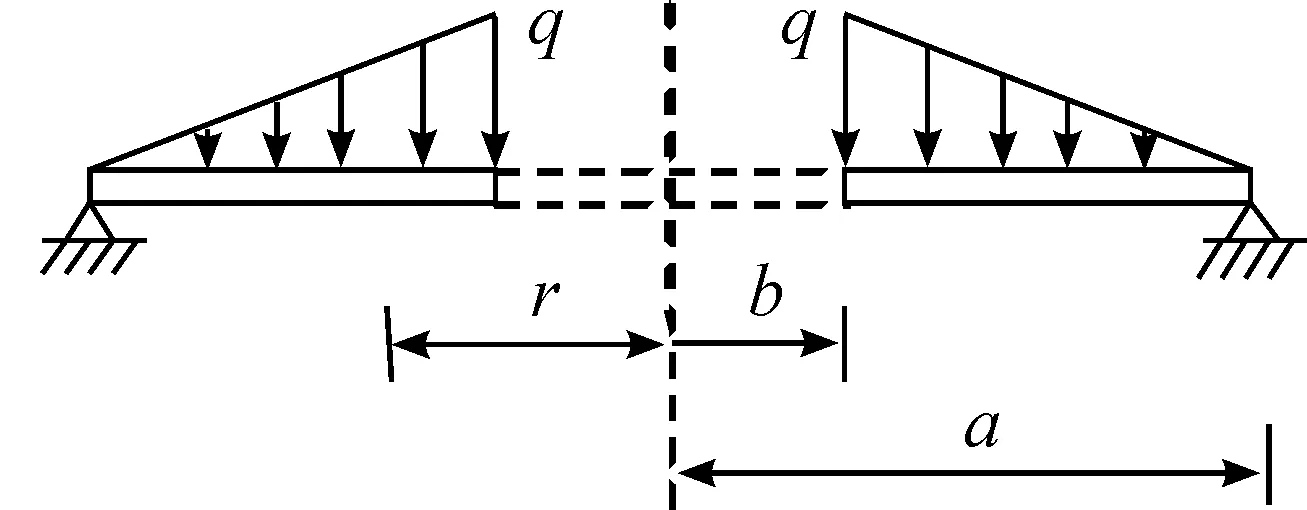
图1 简支环板与荷载示意图

环板的平衡方程为

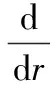
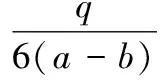
(1)

式中：mr为径向弯矩；mθ为环向弯矩；Qr为剪力；r为环板任一点的半径。

Mises屈服条件为

(2)

其中:m0为环板的塑性极限弯矩。

环板的边界条件为

(3)

根据边界条件，可设试函数为

(4)

式中k1、k2为待定系数，将试函数式(4)分别代入平衡方程式(1)和Mises屈服条件式(2)，得到相应的余量为

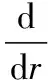
2(r3-b3)]=k1[3r2-2(a+b)r+ab]-

k2[r2-(a+b)r+ab]-mo+

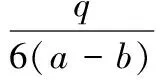
(5)

m0(r-a)(r-b)(2k2-k1)

(6)

采用加权余量法的子域法沿着r方向消除余量

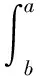
(7)

把式(5)、式(6)代入式(7)得如下方程组

(8)

在方程组(8)中消去k2可得

(a-b)2(a+3b)2q2+2(a-b)3(a+3b)k1q+

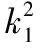
(9)

式(9)中存在两个待求量k1和q,故还不能直接求出极限载荷q，考虑极值条件即dq/dk1=0,解(9)式得

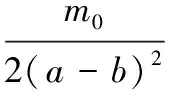
(10)

将式(10)代入式(9),可以求出极限载荷q满足的方程为

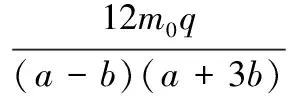
(11)

由式(11)求出的极限载荷为

(12)

2 外边界固支、内边界自由环板在线性载荷作用下的极限载荷

设作用于内边界自由、外边界固支环板上的线性载荷的分布形式如图2所示。

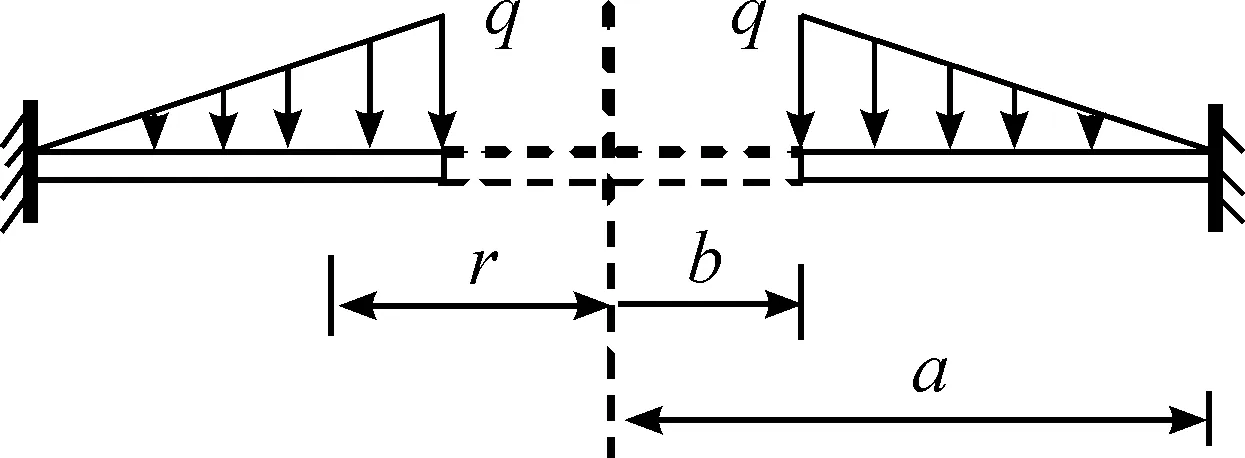
图2 固支环板与荷载示意图

可知，内边界自由、外边界固支环板的平衡方程及Mises屈服条件与式(1)和式(2)相同，仅边界条件不同，此时环板的边界条件为

(13)

根据边界条件，取如下试函数

(14)

将此试函数分别代入平衡方程(1)和Mises屈服条件(2),得余量

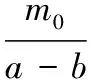
k1[3r2-2(a+b)r+ab]-

k2(r-a)(r-b)+

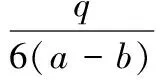
(15)

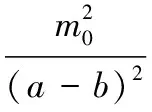
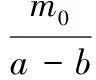
k2(r-a+b)]

(16)

采用加权余量法的子域法沿着r方向消除余量,有

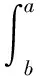
(17)

把式(15)、式(16)代入式(17)，可得

(18)

联立方程组(18)并消去k2,得到

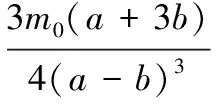
(19)

应用极值条件即dq/dk1=0,解得

q2(a+3b)2(a-b)2+4(a-b)4k1-

6m0k1(a+3b)(a-b)-

3m0q(a+3b)(7a+b)+2k1q(a+3b)(a-b)3+

(20)

将式(20)代入式(19)可得满足极限载荷q的方程为

3(a-b)2(a+ 3b)2q2-6m0q(a+ 3b)(13a-b)+

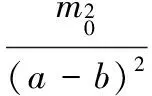
(21)

3 结果分析

通过Mises屈服条件求出了在线性荷载作用下内边界自由、外边界简支和固支两种支撑情况下环板的塑性极限载荷[8-11]。

1) 对于线性载荷作用下外边界简支、内边界自由的环板，其极限载荷为式(12),而用Tresca屈服条件求得的塑性极限解[2]为

(22)

可以看出本文解为用Tresca屈服条件求出的极限载荷的1.129倍，特别地当b=0时，即简支圆板在线性载荷作用下其塑性极限载荷为

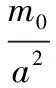
(23)

本文求出的塑性极限载荷qMises为13.547m0/a2，与文献[11]的结果13.487m0/a2极为接近，本文解稍微高于文献[7]的结果，这是由于采用近似的试函数而致，采用不同的试函数，求出的结果也将不同。本文用Mises屈服条件得到的塑性极限载荷略大于用文献[2]用Tresca屈服条件求出的极限解，两种解法得出的极限载荷的规律是一致的。

2) 对于线性载荷作用下外边界固支内边界自由的环板，用数值方法求解式(21),得出不同内外径比情况下的结果如表1所示。

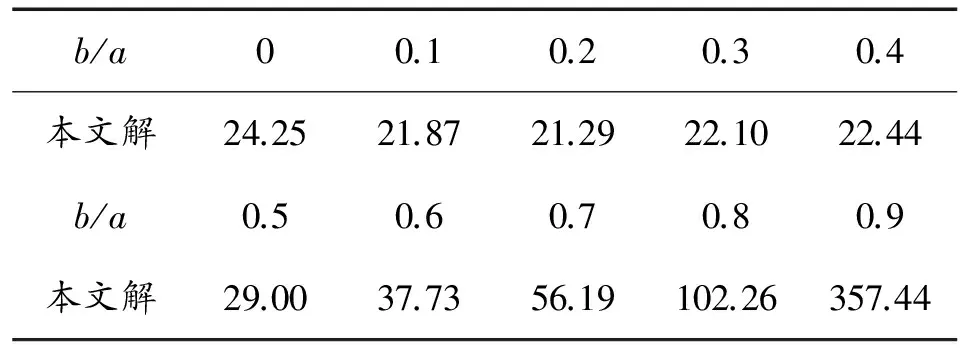
表1 固支环板极限载荷(qa2/m0)

由表1，随着内外半径比值增大，极限载荷先减小后增大。当b/a为零时，此时环板退化成圆板，当外边界固支时，本文求得的极限解为24.25m0/a2,这与文献[5]的结果24.4m0/a2极为接近，从而也说明本文结果是合理的。可见，本文给出的在线性荷载作用下内边界自由、外边界简支和固支两种支撑情况下环板的塑性极限载荷计算公式简洁，避免了最大弯矩极限条件解答中解高次方程的不便，更符合工程应用。

[1] 王仁，熊祝华，黄文彬.塑性力学基础[M].北京：科学出版社,1982.

[2] JONES N.Structural impact[M].Cambridge UK:Cambridge University Press,Cambridge,1989.

[3] 徐秉业,刘信生.结构塑性极限分析[M].北京:中国建筑工业出版社,1985.

[4] 吴向,徐秉业.用加权残数法求环板在Mises屈服条件下的极限载荷[J].力学学报,1989(21):125-130.

[5] 刘福林.用加权余量法分析固支圆板和环板在Mises屈服条件下的极限载荷[J].计算力学学报,2002,19(3):369-372.

[6] 刘福林，赵颖.用Mises屈服条件求内边界简支环板在线性载荷作用下的极限载荷[J].计算力学学报,2003,20(4):504-507.

[7] 蒋朝志,刘东.Mises屈服条件下简支环板的塑性极限荷载[J].土木建筑与环境工程,2007,29(4):87-89.

[8] 赵颖,刘福林,陈勉.线性荷载作用下外固支环板的极限荷载分析[J].哈尔滨工业大学学报,2005,37(1):89-91.

[9] 刘磊.Mises屈服条件在固支圆板塑性极限分析中的应用[J].辽宁大学学报(自然科学版),2003,30(4):317-319.

[10] 洪媛,陈钢.求固支圆板在线性荷载作用下的极限荷载——用加权余量法和Mises屈服条件[J].辽宁大学学报(自然科学版),2005,32(1):36-38.

[11] KARGARNOVIN M H,FAGHIDIAN S A,FARJAMI Y,et al.Application of homotopy-Padé technique in limit analysis of circular plates under arbitrary rotational symmetric loading using von-Mises yield criterion[J].Communications in Nonlinear Science amp; Numerical Simulation,2010,15(4):1080-1091.

(责任编辑杨继森)

LimitLoadforNoSupportedAnnularPlateonInnerBoundaryBasedonMisesYieldCondition

ZHANG Dengxia, CUI Shitang, HU Liming

(Artillery and Air Defense Corps Academy, Heifei 230031, China)

Limit loads are calculated for simple supported annular plate and clamped annular plate on the outer end ut no supported on inner boundary by using Mises yield condition. By choosing suitable trial function and using weighted residual method, the results of the limit loads are got. The numerical results are proved to be reasonable by comparing with the results under Tresca condition.

weighted residual method; Mises yield condition; limit loads; annular plates

2017-07-07；

2017-07-30

张登霞(1976—)，女，硕士，讲师，主要从事机械设计与制造研究。

10.11809/scbgxb2017.11.041

本文引用格式：张登霞,崔世堂,胡立明.Mises屈服条件下内边界自由环板受线性载荷作用下的极限载荷[J].兵器装备工程学报，2017(11):189-191,196.

formatZHANG Dengxia, CUI Shitang, HU Liming.Limit Load for No Supported Annular Plate on Inner Boundary Based on Mises Yield Condition[J].Journal of Ordnance Equipment Engineering,2017(11):181-191,196.

O344.1

A

2096-2304(2017)11-0189-03