航空弹药铁路运输振动响应模型及影响因素分析

於崇铭，任风云，田 丰

(空军勤务学院 航空弹药系， 江苏 徐州 221000)

航空弹药铁路运输振动响应模型及影响因素分析

於崇铭，任风云，田 丰

(空军勤务学院 航空弹药系， 江苏 徐州 221000)

振动对弹药是一个持续的作用过程，主要由各式各样的轨道不平顺综合作用而成；为提高安全性，以某型弹药为研究对象，建立了弹药系统的二自由度振动力学模型；通过实测的加速度信号进行分析，得到弹药系统的动力学参数，并通过施加高斯白噪声激励信号，分析弹药包装对振动的影响；结果表明：通过适当增加弹药包装的质量，选取与弹药本身阻尼比值较小的材料能减少弹药在铁路运输过程中的振动；为该型航空弹药的包装防护和运输提供一定的决策参考。

航空弹药；铁路运输；振动；影响因素

火车在运营过程中，由于铁轨不平顺车辆自身结构的特点及缺陷、运营中的空气动力等因素的共同作用下，会产生垂向和横向的作用力并引起车辆系统的各种振动，进而传递到弹药上[1]。长时间的振动激励会给弹药造成损伤。因此，研究弹药铁路运输振动特性及包装安全性很有必要。

对振动特性的研究主要集中在计算机仿真上。相关研究通过ANSYS软件，应用有限元法对计算机主机在运输过程中的振动特性进行了计算机仿真，求出了包装件的固有频率与固有阵型，以及频域/时域的动态响应[2]。通过建立某装药弹的模态方程，采用ANSYS软件对该弹的振动特性进行了数值模拟利用Block Lanczos法求解，得到前10阶振动固有频率和振型。提出应用三维有限元单元和导弹实体简化模型，对某战术导弹运输环境中结构振动特性进行分析，进而对导弹水平支承条件下的固有频率和振型进行了计算，为运输导弹可靠性分析提供了思路[3]。包装领域在动力学系统方面的研究为我们提供了很好的借鉴。特别是将频域逆子结构分析方法引入包装动力学领域，并采用集总参数模型法验证其合理性，进而准确预测包装系统各部件的动态响应特性[4]，这些都为弹药铁路运输动力学特性分析提供了理论指导。

由于通过计算机仿真缺乏一定的验证，所以往往得不到精确的计算结果；另外实际系统及其部件间存在复杂的耦合关系，在实测系统中，存在着激励点和响应点的选择问题，选择不当易导致较大失误，使得逆子结构理论在弹药领域应用也存在一定的局限性。

综上所述，通过将集中质量与仿真两种方法结合起来，进行计算，能够模拟弹药铁路运输的实际响应情况。

1 航空弹药振动模型建立

1.1 预分析与模型建立

某型航空弹药的铁路运输振动研究主要是考虑振动对装药的影响。首先，要建立弹药铁路运输振动模型。铁路运输属于各态历经性的平稳随机振动，振动频率主要集中在5～150 Hz之间。振动是同时发生在3个方向，但如表1所示，垂向的加速度在列车正常运行时明显比列车横向、纵向的大[5]。因此，研究垂向振动更具意义。

表1 铁路运输过程中最大振动加速度

力学模型的构建应从两个方面考虑：该型弹药外包装与火车车厢底板之间的振动传递；弹药主体与包装箱之间的振动传递。因此，拟建立如下图所示弹药铁路运输振动模型。弹药二自由度系统的简单模型如图1所示。

图1中，m1，m2分别为弹药、弹药外包装箱的等效质量；k1，c1分别为弹药与包装箱之间的刚度和阻尼值；k2，c2分别为弹药包装箱与火车车厢底板的刚度和阻尼值；x1，x2，y分别为弹药、弹药包装箱及车厢底板的相对静止状态平衡位置的位移。至此，弹药铁路运输模型建立完成。

图1 弹药运输二自由度模型

1.2 建立方程

在物理坐标系统中，一个典型的多自由度线性非时变系统的运动微分方程为

[M]{x″(t)}+[C]{x′(t)}+[K]{x(t)}={f(t)}

(1)

式(1)中：[M]、[C]、[K]分别为系统的质量矩阵、阻尼矩阵和刚度矩阵；{f(t)}为激振力向量；{x(t)}、{x′(t)}、{x″(t)}分别为结构的位移响应、速度响应及加速度响应向量。

结合所建立的弹药振动模型，用拉格朗日法列出以下振动微分方程组：

2 参数识别

首先通过DT-178A运输测振仪测得弹药、包装箱及车厢底板的垂向振动加速度[6]。由于振动方程中含有速度、位移量，所以需要对测得的加速度信号进行积分，以便于分析。

通过Matlab的cumtrapz(x，y)函数对离散加速度信号进行积分，得到同一时刻车厢底板、弹药包装笼、弹药的垂向振动响应。如表2、表3、表4所示，分别列出了车厢底板、弹笼、弹体的测试计算参数。

表2 车厢底板测试及计算参数

表3 弹笼测试及计算参数

表4 车厢底板测试及计算参数

通过最小二乘法(Least Square)对C,K进行拟合。因为振动方程组为k，c的线性方程组，通过上述计算的数值代入将得到一个超定方程组，得不出精确解。而通过线性回归可以让K和C的平均数落在一条直线上，换句话说，用最小二乘法可以让数据中尽可能多的点落在同一条直线上，即求最优解[7]。通过Matlab的拟合，得到该型弹药的振动模型动力学参数，如表5所示。

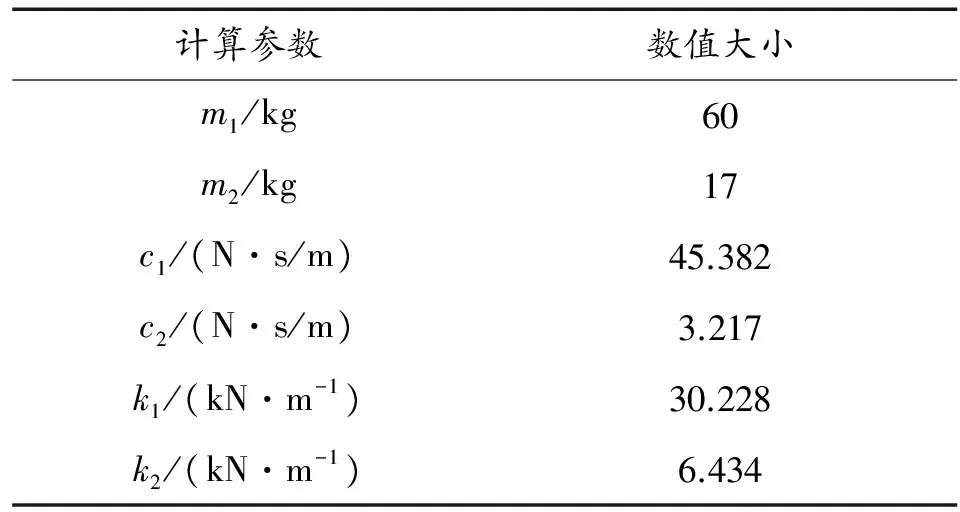
表5 弹药振动模型动力学参数

3 白噪声激励与振动特性分析

构建好模型后，需要选择一个激励信号。选择激励信号是进行振动特性分析的重要环节，必须根据被测结构特点、振动环境等因素选取恰当的激振信号。白噪声信号，在整个时间历程上都是随机的，不具有明显的周期性；在频率域上是一条平直的直线，包含从零开始到无穷大的频率成分，且任何频率成分所包含的能量是相等的，完全符合铁路运输振动的特性。白噪声的功率谱密度图像如图2所示。

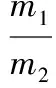
将振动方程转换到状态空间下，

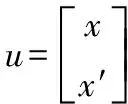
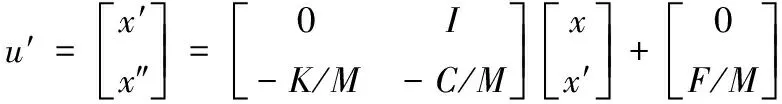
采取单因素数值分析方法[8]和欧拉计算法[9]，即保持其他各影响因素不变，分析振动响应随其中某一变量变化的情况。

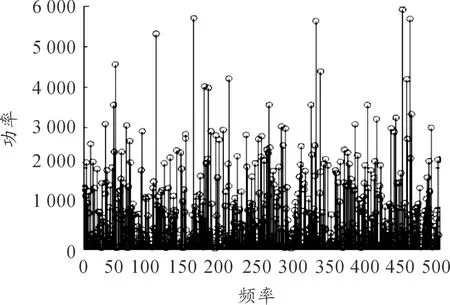
图2 白噪声功率谱密度图像

首先分析弹药包装箱和弹药主体的质量比对振动的影响。

1) 质量比。由图3可见，当质量比达到某一值时，弹药振动响应达到最大，这也容易理解，可能产生共振。弹药的质量是不可以改变的，因此，为避免发生共振，减少弹药振动响应，要适当增大弹药包装m2的值。

2) 阻尼比。保持其他各因素不变，改变阻尼比的大小。由图4、图5可见，随着阻尼比的增大，弹药振动响应呈线性增长的趋势。为此，该型弹药包装要选取与弹药本身阻尼比值较小的材料。

3) 振动激励。虽然白噪声激励是随机振动信号，但振动激励越大，弹药振动响应就越大。这也容易理解，火车的振动激励与铁轨平整度、火车运行速度等都有联系。具体内容涉及到列车动力学部分[10]，本文不再考虑。

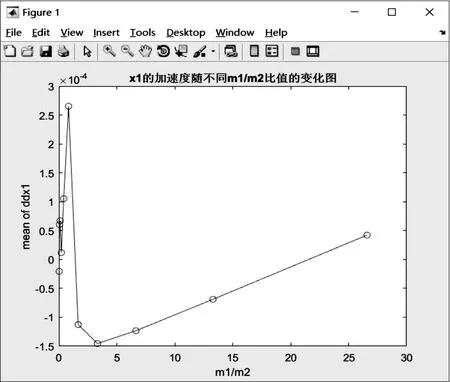
图3 质量比对弹药振动响应影响

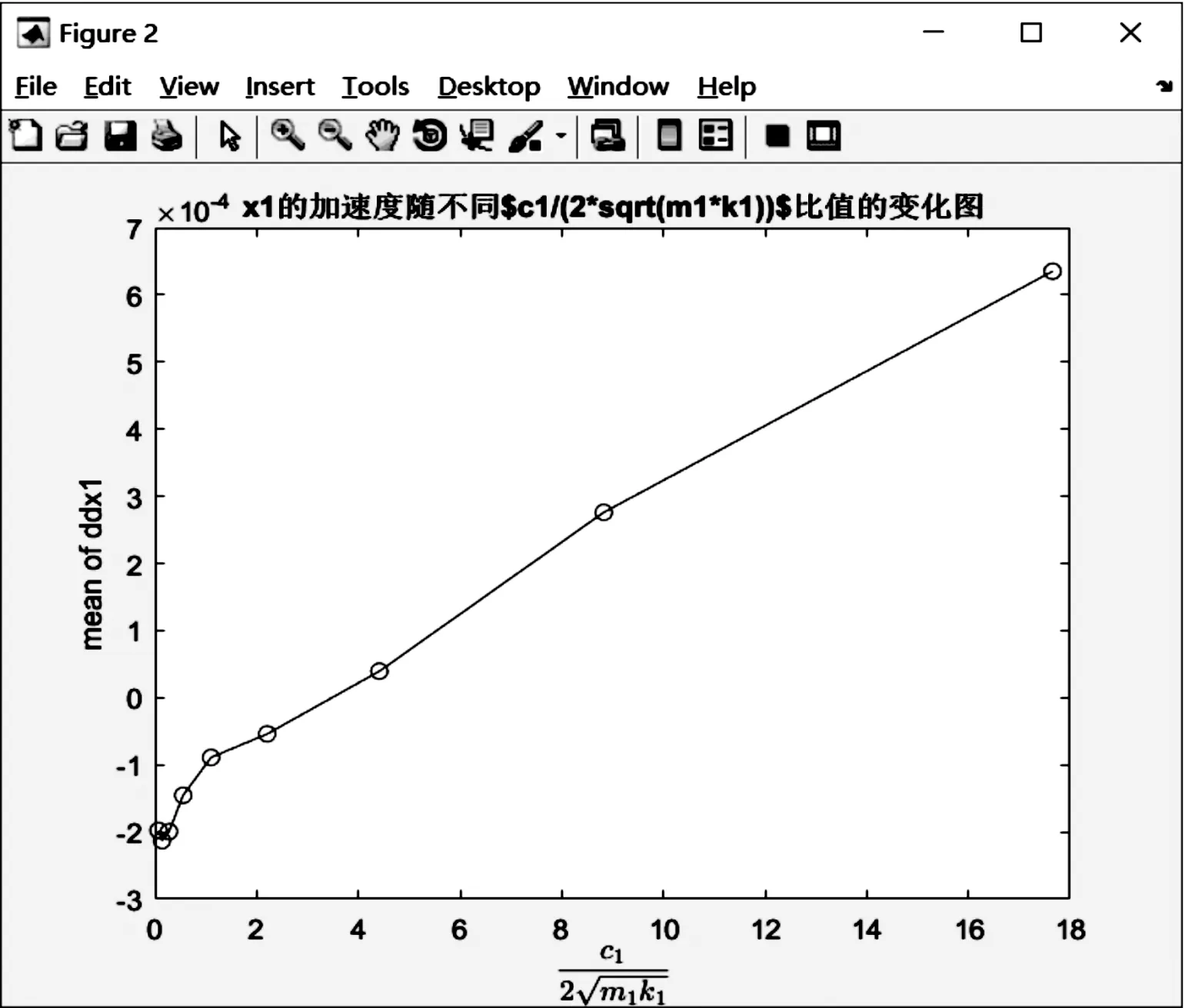
图4 ξ1对弹药振动响应影响

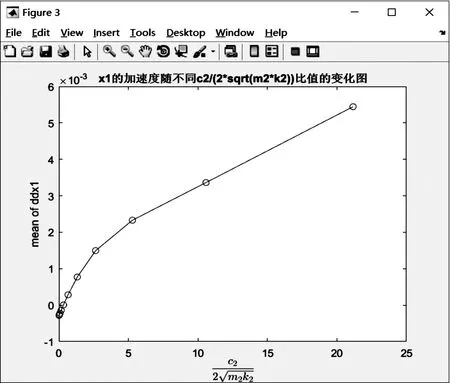
图5 ξ2对弹药振动响应影响

4 结论

本文通过建立弹药铁路运输振动方程，通过MATLAB对测得的离散加速度信号积分识别出动力学参数，并分析质量比、阻尼比、振动激励对弹药振动响应的影响，通过适当增加弹药包装的质量，选取与弹药本身阻尼比值较小的材料能减少弹药在铁路运输过程中的振动。

[1] 刘乘，卢杰，陈满儒.运输包装件振动特性的计算机仿真[J].包装工程,2002,23(4):20-22.

[2] 冯翔，李向斌，关正西，等.运输环境中某战术导弹结构振动特性分析[J]固体火箭技术，1999(1)：6-10.

[3] R.克拉夫，J.彭津.结构动力学[M].北京：高等教育出版社，2006:14-16.

[4] 刘佳丽.铁路运输货物包装件冲击振动分析[J].兰州交通大学学报，2009(5):48-51.

[5] 汤伯森.包装动力学[M].北京:化学工业出版社，2011:21-25.

[6] 曹树谦，张文德.振动结构模态分析[M].天津:天津大学出版社，2015：111-114.

[7] 李海广.弹药公路运输振动特性及安全性评估研究[J].军械工程学院，2014:18-24.

[8] 温正.精通MATLAB智能算法[M].北京:清华大学出版社，2015:365-367.

[9] LIANG Cho-chung,CHIANG Chi-feng.A Study on biodynamic models of seated human subjects exposed to vertical vibration[J].International Journal of Industrial Ergonomics,2006,36(10):869-890.

[10] 罗芝华，刘涛，陈文芳.铁道车辆工程[M].长沙：中南大学出版社，2014：438-439.

(责任编辑唐定国)

AviationAmmunitionVibrationResponseModelandInfluenceFactorsAnalysisofRailwayTransportation

YU Chongming, REN Fengyun, TIAN Feng

(Department of Aviation Ammunition, Air Force Logistics College, Xuzhou 221000, China)

Vibration on the role of ammunition is a continuous process, which consists of all kinds of track irregularities. In order to improve the security, to a certain type of ammunition as the research object,a two degree of freedom vibration mechanics model of ammunition system is established. The kinetic parameters of ammunition system are obtained by analyzing the measured acceleration signal, and the influence of the ammunition packaging on vibration is analyzed through applying the Gaussian white noise excitation signal. The results show that the ammunition vibration in railway transportation can be reduced by increasing the quality of ammunition package and reducing the damping ratio of ammunition itself. It will provide some reference for the packing, protection and transportation of the aviation ammunition.

aviation ammunition; railway transportation; vibration; influence factors

2017-06-12 ；

2017-07-20

於崇铭(1992—)，男，硕士研究生，主要从事装备理论与装备技术研究。

机械制造与检测技术

10.11809/scbgxb2017.11.033

本文引用格式：於崇铭，任风云，田丰.航空弹药铁路运输振动响应模型及影响因素分析[J].兵器装备工程学报，2017(11):151-154.

formatYU Chongming, REN Fengyun, TIAN Feng.Aviation Ammunition Vibration Response Model and Influence Factors Analysis of Railway Transportation[J].Journal of Ordnance Equipment Engineering,2017(11):151-154.

U268.6

A

2096-2304(2017)11-0151-04