寻本求源

石有山

2017年高考天津卷压轴题第12题，综合了电容器，导体棒切割磁感线，动量定理等知识，是一道综合性很强的习题。但该题实质是由几道简单经典试题组合而来，熟练掌握原始模型，重视平时的基础，压轴题也有似曾相识的感觉，有原题的味道，解出压轴题并没有想象中的难度。

（一）经典原题

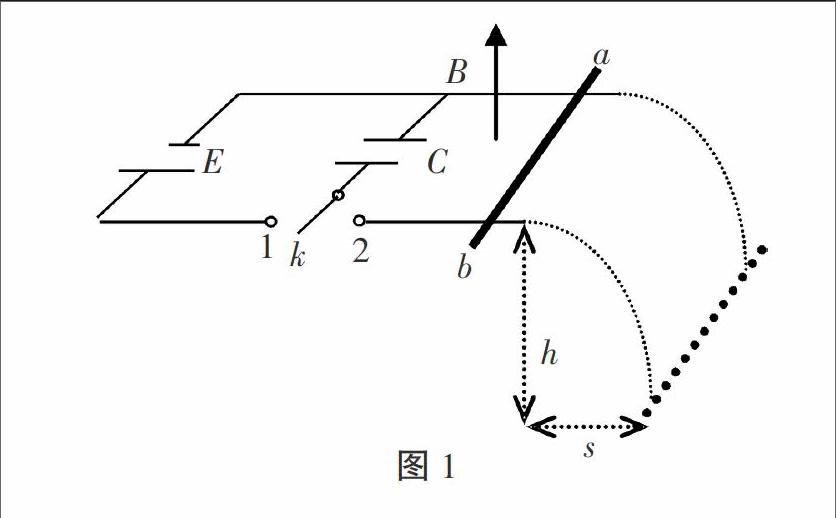
【例1】如图所示，金属棒ab的质量m=5g，放置在宽L=1m光滑平行金属轨道边缘处，两金属导轨处于水平面内，该处有竖直向上的匀强磁场，磁感强度B=0.5T，电容器的电容C=200uF，电源电动势V，导轨平面距地面高度h=0.8m，g取10m/s2。在开关k与1接通稳定后，再把k扳到2接通，则金属棒被抛到s=0.064m的地面上，试求电容器两极板的剩余电量是多少？

解析：金属棒抛出后水平方向v=■

竖直方向h=■gt2

金属棒被抛出的瞬间过程BIL？驻t=mv

q=I？驻t

原来电容器上的电量Q=CE

金属棒被抛出电容器上剩余的电量为Q-q=1.6×10-3C

结论1：应用动量定理可以求变力的冲量，这时可以求出该力作用下物体动量的变化量，用动量的变化量等效代替变力的冲量。若导体棒只受安培力或安培力远大于其它外力，则由动量定理得：BIL？驻t=mv2-mv1，又因为q=I？驻t，故BqL=mv2-mv1，利用动量定理可以求得安培力作用下通过某个截面的电量。

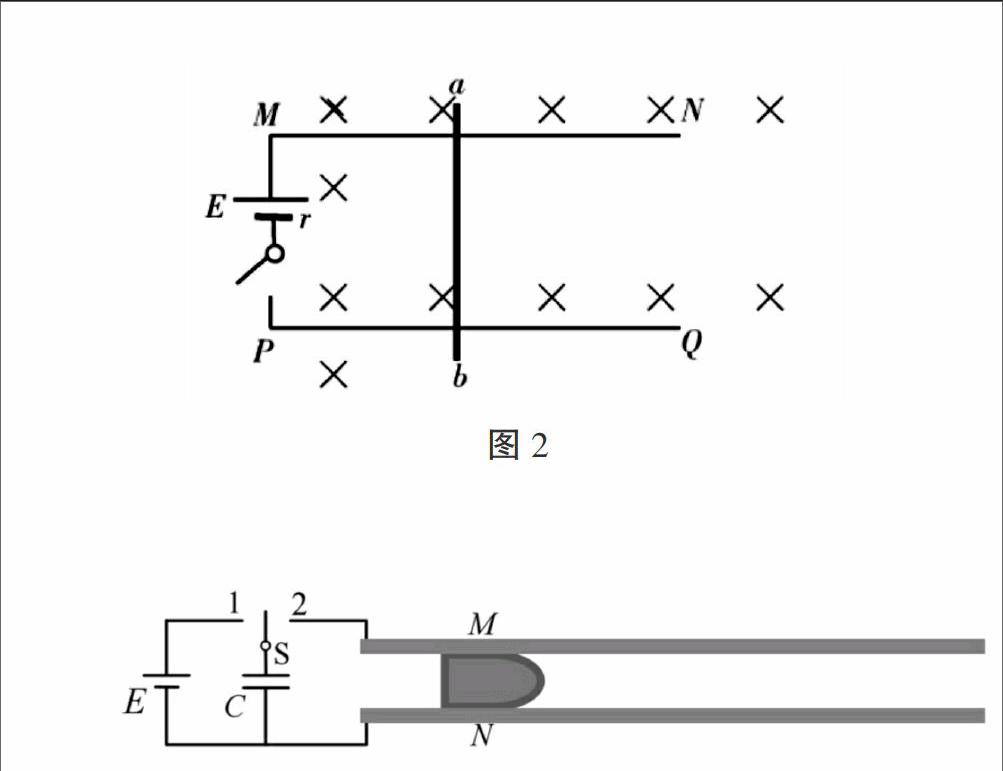
【例2】如图2所示，长平行导轨PQ、MN光滑，相距l=0.5m，处在同一水平面中，磁感应强度B=0.8T的匀强磁场竖直向下穿过导轨平面。横跨在导轨上的直导线ab的质量m=0.1kg、电阻R=0.8？赘，导轨电阻不计。导轨间通过开关S将电动势E=1.5V、内电阻r=0.2？赘的电池接在M、P两端，试计算分析：导体ab的加速度的最大值和速度的最大值是多少？

解析：在S刚闭合的瞬间，导线ab速度为0，没有感应电流，由a到b的电流I0=■=1.5A，ab受安培力水平向右，此时ab瞬时加速度最大，加速度a0=■=■=6m/s2。

导体棒ab向右运动切割磁感线，产生感应电动势，根据右手定则，感应电动势产生的电流方向与电动势E产生的电流方向相反，回路电流减小，导体棒ab受水平向右的安培力减小，导体棒做加速度逐渐减小的加速运动。当感应电动势E/与电池电动势E相等时，ab的速度达到最大值。此时回路内的电流为0，导体棒做匀速运动。根据上述的分析可知E-Blvm=0，所以vm=■=3.75m/s。

结论2：在匀强磁场中导体棒不受其它外力时，导体棒外接直流电源，导体棒做加速度逐渐减小的加速运动，最大加速度为导体棒接通瞬间，终极状态为导体棒做匀速运动，导体棒由于电磁感应带来的电动势和原电动势大小相等，回路内的电流为0，安培力为0。

（二）2017年天津卷压轴第12题

【例3】电磁轨道炮利用电流和磁场的作用使炮弹获得超高速度，其原理可用来研制新武器和航天运载器。电磁轨道炮示意如图3所示，图中直流电源电动势为E，电容器的电容为C。两根固定于水平面内的光滑平行金属导轨间距为l，电阻不计。炮弹可视为一质量为m、电阻为R的金属棒MN，垂直放在两导轨间处于静止状态，并与导轨良好接触。首先开关S接1，使电容器完全充电。然后将S接至2，导轨間存在垂直于导轨平面、磁感应强度大小为B的匀强磁场（图中未画出），MN开始向右加速运动。当MN上的感应电动势与电容器两极板间的电压相等时，回路中电流为零，MN达到最大速度，之后离开导轨。问：

（1）磁场的方向；

（2）MN刚开始运动时加速度a的大小；

（3）MN离开导轨后电容器上剩余的电荷量Q是多少。

解析：（1）MN开始向右加速运动，电流方向从M到N，根据左手定则，磁场方向垂直于导轨平面向下

（2）电容器完全充电后，两极板间电压为E，当开关S接2时，电容器放电，设刚放电时流经MN的电流为I，有

I=■①

设MN受到的安培力为F，有

F=IlB②

由牛顿第二定律有

F=ma③

联立①②③式得

a=■ ④

（3）当电容器充电完毕时，设电容器上电量为Q0，有

Q0=CE ⑤

开关S接2后，MN开始向右加速运动，速度达到最大值vmax时，设MN上的感应电动势为E′，有

E′=Blvmax ⑥

依题意有

E′=■ ⑦

设在此过程中MN的平均电流为■，MN上受到的平均安培力为F，有

F=■lB ⑧

由动量定理，有

F？驻t=mvmax-0 ⑨

又■？驻t=Q0-Q ⑩

联立⑤⑥⑦⑧⑨⑩式得

Q=■ ？輥？輯？訛

点评：本题的模型和例1的模型非常相似，即先给电容器充电，后电容器通过导体棒放电，导体棒由于安培力的作用运动，电容器的放电量都通过动量定理求出。所不同的是例1导体棒的末速度通过平抛运动求得，天津高考题的导体棒的末速度，通过导体棒在匀强磁场中的运动模型求出。从例2可以看出，在匀强磁场中导体棒不受其它外力时，导体棒最大加速度为导体棒接通瞬间，导体棒终极状态为导体棒两端的电动势大小与外接电源的电动势大小相同，对于天津高考题，导体棒两端的电动势与放电后电容器两端的电压相等。本题求解（2）问与例2完全相同，求解（3）问结合了例1和例2两种思想。

（三）变式巩固

【例4】如图4所示，水平导轨两端接有电容C，一有效长度为l的导体棒跨接在导轨上，不计导体棒与导轨间的摩擦，现给导体棒一个向右的初速度，则在导体棒向右运动的运动中，下列说法正确的是（ ）endprint

A. 开始时导体棒的加速度最大

B. 导体棒最后做匀速运动

C. 导体棒最后静止在导轨上

D. 回路中最终的感应电流为0

解析：导体棒相当于电源，导体棒向右运动的过程中，电容器被充电，极板上的电压U逐渐增大，导体棒受到向左的安培力，导体棒的运动速度减小，导体棒的感应电动势减小，设导体棒的速度减小为v时，U=Blv，此时回路内的电流为0，导体棒受到的安培力为0，导体棒做匀速运动，选项BD正确、C错误，导体棒向右做加速度逐渐减小的减速运动，开始时导体棒的加速度最大，选项A正确。

点评：本题和例2的区别在于例2有直流电源，导体棒运动过程中产生的电动势为反电动势，本题导体棒为电源，电容器上的电压为反电动势，但问题的本质都相同，当回路内的感应电流为0时，即总电动势为0时，导体棒的速度取极值。

【例5】如图5所示，“质量m=3.0×10-3kg的“ ■ ”型金属细框竖直放置在两水银槽中，“ ■ ”型框的水平细杆CD长l=0.20m，处于磁感应强度大小B=1.0T、方向水平向右的匀强磁场中，电源电动势E= 16V，通过通过开关k，电容C=2mF，与两水银槽相连，在开关k与1接通稳定后，再把k扳到2接通，瞬间细框跳起（细线跳起瞬间安培力远大于重力），跳起的最大高度h=0.20m。试求

（1）跳起过程通过CD棒的电量为多少？

（2）跳起后电容器两极板的电压是多少？

解析：根据动量定理细线跳起瞬间B1Il？驻t-mg？驻t=mv

细线跳起瞬间安培力远大于重力，重力冲量忽略不计

q=I？驻t

跳起后机械能守恒mgh= ■mv2

解得 q=0.03C（2分）

（2）原来电容器上的电量Q=CE

金属棒被抛出电容器两极板的电压 U=■

解得U=1V

答案：（1）0.03C （2）1V

点评：本题和例1情景、求法基本一致，只不过该题用竖直上抛，求导体棒离开水银槽的速度。

天津卷压轴题第21题，看似一道新情景习题，实际是可以转化为上面两个重要结论的应用，有原题的味道，解题时要学会转化。题目设计和两种经典习题相比，创设新颖，构思巧妙，导体棒的终极速度通过两个电动势大小相等联系了电容器上的剩余带电量，导体棒的终极速度通過动量定理联系了电容器的放电量，从而根据电量守恒建立方程求解。本题考查学生提取、加工信息，并利用相关信息进行转换的能力。

责任编辑 李平安endprint