利用线性平均值巧解电磁感应问题

(辽宁省凌源市职教中心，辽宁 朝阳 122500)

利用线性平均值巧解电磁感应问题

郑金

(辽宁省凌源市职教中心，辽宁 朝阳 122500)

本文归纳了线性函数平均值的两个公式及性质，利用线性平均值公式，巧妙解答有关导体棒在各种磁场中运动、垂直切割磁感线时产生感应电动势和感应电流的问题。

线性平均值；电磁感应；导体棒；安培力

在有关电磁感应问题中常见的磁场有三种，其一是稳恒匀强磁场，即磁感应强度处处相同，而且不随时间变化；其二是随时间均匀变化的匀强磁场；其三是随空间均匀变化的稳恒磁场。在闭合电路中的导体棒切割磁感线的过程中，某些物理量可能随时间线性变化，也可能随位移线性变化，因此需计算平均值。下面按磁场的不同特点,从三方面举例分析。

1 恒定匀强磁场问题

例1：如图1所示，两条水平放置、彼此平行的光滑金属导轨MN、PQ，间距为L，匀强磁场垂直于导轨平面，磁感应强度为B，导轨左端接阻值为R的电阻。垂直于导轨跨接金属杆ab，质量为m，电阻为r，导轨电阻不计。现用水平恒力F向右拉ab杆，使之从静止开始运动，经时间t位移为s，速度为v，求在时间t内流过金属杆的电流的平均值以及电荷量。

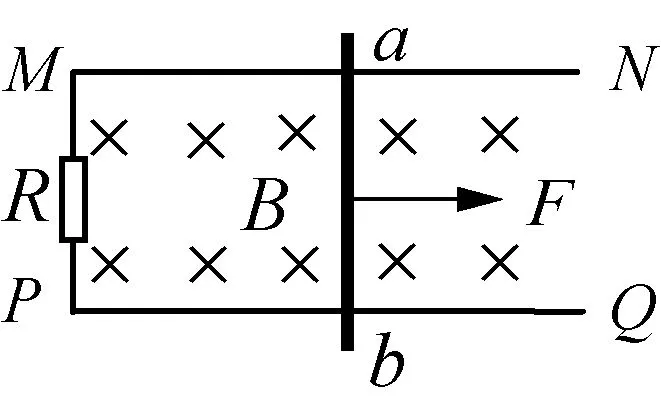
图1

点评：求感应电动势时应利用平均值公式，而不用瞬时值公式。求电荷量必须利用电流的平均值，而不能利用瞬时值或有效值。解方程需要一定的技巧，即在求电流的平均值时以BL为整体消去未知量。

例2：如图2所示，光滑的平行金属导轨水平放置，电阻不计，间距为l=1m，左端接有阻值为R=0.3Ω的电阻。在区域cdef内存在垂直于导轨平面向下的有界匀强磁场，其边界宽度为s=1m，磁感应强度的大小为B=0.5T。一质量为m=1kg，电阻为r=0.2Ω的金属棒置于导轨上，与导轨垂直且接触良好，以初速度v0=2m/s从磁场的左边界开始向右运动，并越过磁场的右边界，假设金属棒MN在运动过程中始终受到大小与速度成正比的阻力f=kv(k=0.3Ns/m)。求：(1) 金属棒MN离开磁场时的速度v；(2) 电路中产生的焦耳热。

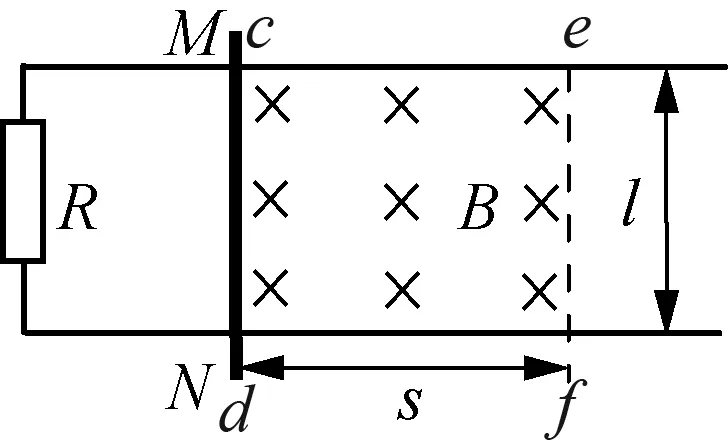
图2

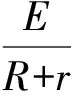
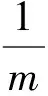
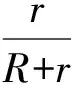
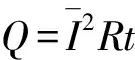
2 随时间均匀变化的匀强磁场问题

例3：如图3所示，两平行金属导轨MN、PQ固定在绝缘水平面上，间距为L=1.0m，图中MP、ab、cd、ef之间的距离也为L=1.0m。导轨MN、PQ和导线MP单位长度的电阻为R0=0.1Ω，虚线ab右侧空间存在匀强磁场，方向竖直向下，且磁感应强度大小随时间的变化关系式为Bt=(0.2+0.1t)T，导体棒的电阻不计。若导体棒在外力作用下以2m/s的速度匀速向右运动，在t=0时刚好经过cd处，求：(1) 导体棒从cd处运动到ef的过程中安培力的冲量为多大？(2) 安培力做的功为多少？(3) 电路中产生的焦耳热为多少？

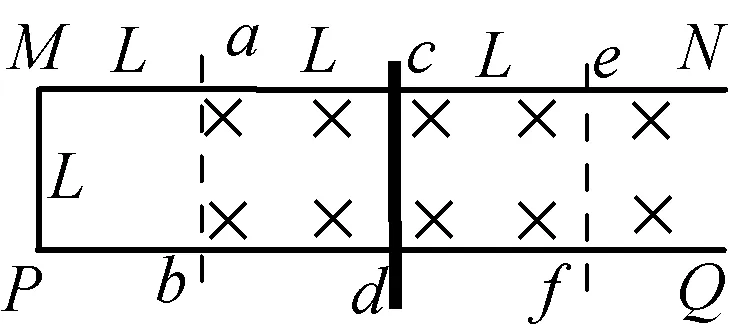
图3

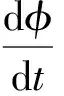
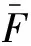
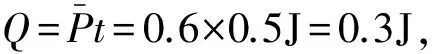
点评：在导体棒切割磁感线的同时，磁场还随时间变化，因此电路中产生两种感应电动势，即动生电动势和感生电动势。在求解电路中总的感应电动势时，利用了法拉第电磁感应定律的瞬时值表达式，而不是平均值表达式，要注意回路的面积与回路中磁场区域的面积不相同。在求解冲量、功和热量时，关键是推导出安培力和电功率的瞬时表达式。

3 随空间均匀变化的稳恒磁场问题

例4(2013年上海高考压轴题)：如图4所示，两根相距l=0.4m、电阻不计的平行光滑金属导轨水平放置，一端与阻值R=0.15Ω的电阻相连。导轨xgt;0一侧存在沿x方向均匀增大的稳恒磁场，其方向与导轨平面垂直，变化率k=0.5T/m，x=0处磁场的磁感应强度B0=0.5T。一根质量m=0.1kg、电阻r=0.05Ω的金属棒置于导轨上，并与导轨垂直。棒在外力作用下从x=0处以初速度v0=2m/s沿导轨向右运动，运动过程中电阻上消耗的功率不变。求：(1) 回路中的电流；(2) 金属棒在x=2m处的速度；(3) 金属棒从x=0运动到x=2m过程中安培力做功的大小；(4) 金属棒从x=0运动到x=2m过程中外力的平均功率。

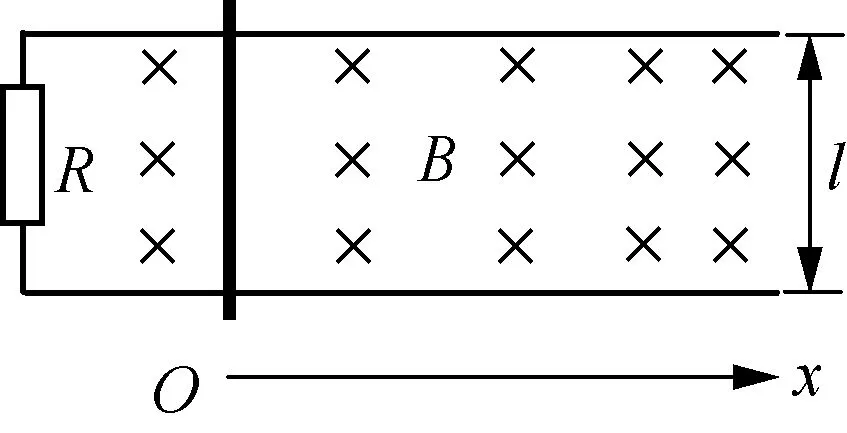
图4

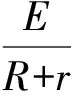
点评：本题解答的关键是利用金属棒克服安培力做的功等于焦耳热以及焦耳定律来求运动时间，而在求解外力的平均功率时，因难以推导外力的瞬时值表达式，只能应用动能定理求出外力做的功，与时间的比值即为平均功率。要注意安培力对金属棒做的功为负值，而金属棒克服安培力做的功则为正值。

[1] 尹绪清.一道电磁学题的析与解[J].中学物理，2009，(3).

[2] 袁芳,朱炯明.功、动能和机械能[J].物理教学，2013，(7).

[3] 金红.电磁感应教学中一个容易忽视的问题[J].物理通报，2016，(6).

[4] 李元法.运用动量定理妙解电磁感应中的单杆问题[J].物理之友,2017,(5).

[5] 应德勇.浅析平均值法在电磁感应问题中的应用[J].中学生数理化(高三)，2016,(5).

[6] 廖启海,杨燕燕.关于电磁感应中金属棒运动位移题析[J].物理之友,2016,(3).

[7] 臧立志.线性函数的平均值在高中物理中的应用[J].物理教师,2010,(4).