1951～2015年沂河年径流量时间序列演变趋势分析

沈亚楠 秦景河 李焕芝

1951～2015年沂河年径流量时间序列演变趋势分析

沈亚楠1秦景河1李焕芝2

水资源短缺已逐渐成为全球性问题，如何有利加强水资源调度，合理分配进而缓解水资源匮乏，急需增强流域内有限的水资源利用效率。所谓河流水资源，即经大气降水或冰雪融水最终汇入河流水系的水，且能为人类生产生活提供帮助，是维持河流和地区生态环境平衡的重要载体，是地表水资源的重要组成部分。随着人类改造自然能力与日增进，流域内径流量出现显著的变化，针对河川径流演变趋势规律以及所影响因素研究逐渐受到广泛的重视。研究河流年径流量动态规律，以可持续发展战略为指导，制定相应水资源使用条例，丰水期按相关规程放水，枯水期进行蓄水，从而促进经济、环境、社会的协调发展。

一、流域概况

沂河发源于山东省境内沂源县的鲁南山麓，位于淮河流域，为沂沭泗最大水系中最大的山洪河道，水流湍急，暴涨暴落，水土流失相对严重，历史上洪水灾害严重，沂河洪水、水资源安全与鲁南、苏北大部分地区的人民生命财产安全及社会经济可持续发展密切相关。沂河流经临沂，被临沂人民称为“母亲河”，到江苏省新沂市最终注入骆马湖，河道全长333km，流域总面积11820km2。在沂河临沂站以上的水系经勘测大致呈现扇形，洪水迅猛。自临沂城以下，进入平原，地面高程也由70m逐渐下降至40m左右，纵坡降为1∶2000～1∶3000。

二、径流序列分析方法

1.小波函数

小波分析的原理是由一簇小波函数系来表示或逼近某一信号。它是指能够迅速衰减到零以及具有震荡性的一类函数，即小波函数满足：

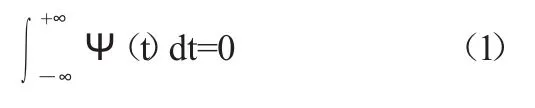
式中：Ψ（t）为基小波函数，通过尺度的伸缩和时间轴上的平移构成函数系：

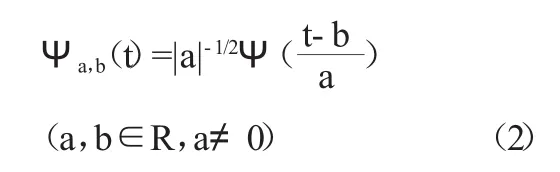
式中：Ψa，b（t）为子小波；a为尺度因子，反映小波的周期长度；b为平移因子，反应时间上的平移。需要进行说明的是，在实际应用研究中，针对具体情况选择所需的基小波函数；采用复数形式的Morlet小波作为母小波函数，因为复数小波的实部和虚部的位相差为π/2，由复小波变换系数的模作为判别水位资料中包含的各尺度周期性的规律及这些周期在时域中分布的判据，能够很好地消除用实型小波变化系数作为判据时所产生的虚假震荡，优化分析结果。

2.小波变换

若Ψa，b（t）是由（2）式所给出的子小波，对于其给定的能量有限信号f（t）∈L2（R），其连续小波变换为：

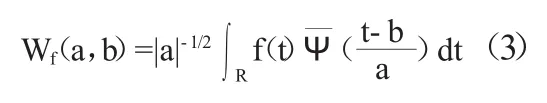
式中：Wf（a，b）为小波变换系数；f（t）为一个信号或平方可积函数；a为伸缩尺度；b平移参数；为的复共轭函数。地学中观测到的时间序列数据大多是离散的，设函数f（kΔt），（k=1，2，…，N；Δt为取样间隔），则式（3）的离散小波变换形式为：

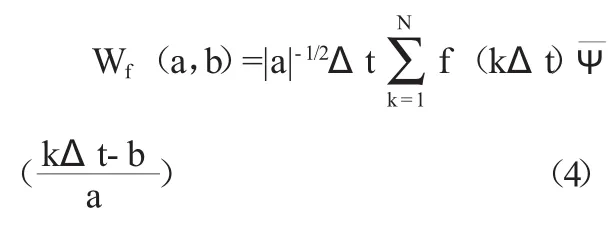
3.小波方差

将小波系数的平方值在b域上积分，就可得到小波方差，即：

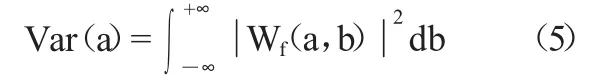
小波方差随尺度a的变化过程，可得出小波方差图。不同尺度a信号波动的能量分布可由公式表达，因此，信号中不同种尺度扰动的相对强度和存在的主要时间尺度可由小波方差图来确定，即主周期。

4.径流序列的多尺度分析的步骤

（1）连续小波变换。径流序列，基于MATLAB小波工具包，选择Morlet小波函数进行连续小波变换，进行数据处理，得到小波系数方差、模和实部。

（2）分析径流的丰枯变化趋势。小波系数实部图，包含着给定时间和尺度信号相对于其他时间和尺度信号的强度关系。通过小波系数实部图由正到负的变化规律，进而确定各时间尺度下，径流序列的丰枯变化规律。

三、径流序列小波特征

河川径流变化不存在真正意义上的周期性质，在时间序列研究分析中，通常含有周期性成分，但是它只是概率意义上的周期，而不是严格的周期，在时域中存在有多层次时间尺度结构以及局部化特征。时间序列小波分析可以有效针对这一要求，通过伸缩和平移等运算功能对函数或信号序列进行多尺度细化分析，研究不同周期随时间的演变情况。

1.年径流量线性统计

本文选用临沂站1951～2015年期间沂河历年的年径流量资料，对其进行线性统计分析（见图1）可知，近65年来年径流量整体呈现减少趋势，趋势线如图斜率为-0.3497，1966年是年均年径流量最大的一年，2015年是年均径流数据量最小的一年。

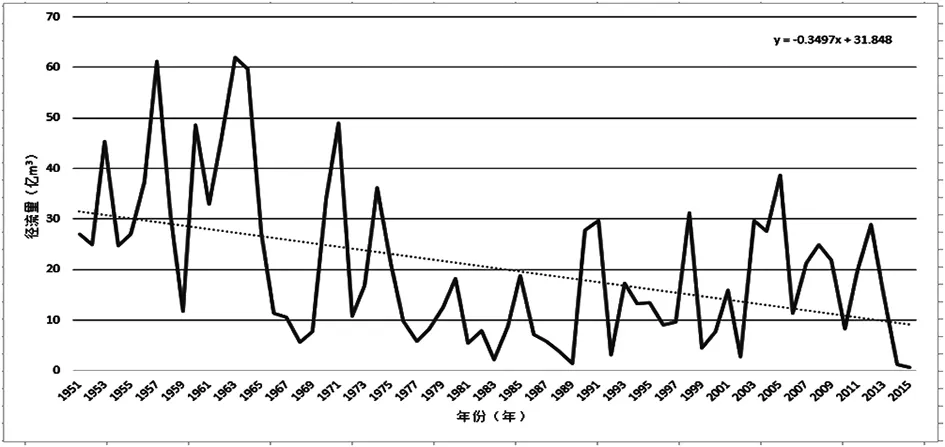
图1 沂河1951～2015年年径流量变化趋势图

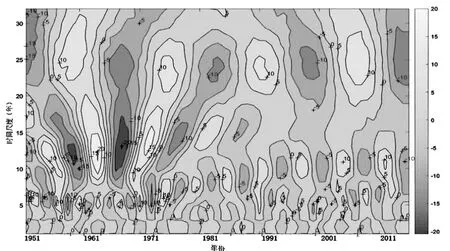
图2 沂河年径流量Morlet小波变换系数实部图

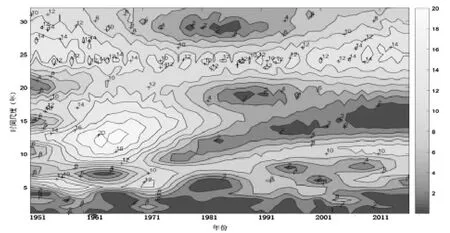
图3 沂河年径流量Mrolet小波变换系数模图

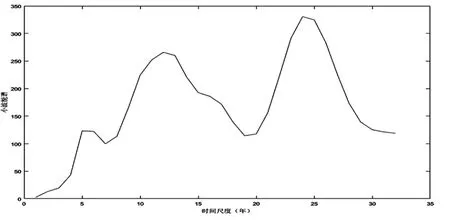
图4 沂河年径流量小波方差图

2.年径流量时间序列小波分析

本文所选Morlet小波为复小波函数，作为其两个重要变量，小波变换系数模，实部，做出相应等值线图。小波变换模值的表示能量密度，模值图可把各种不同时间尺度的周期规律，在时间区域中分布情况展示出来，模值越大，周期变化愈加明显。实部表示给定时间与尺度信号相对与其他时间和尺度信号的强度信息。小波系数值不是真正意义上径流量值，但是二者存在正相关关系，某一时间尺度的正小波系数与该时间尺度下径流量变化的丰水期对应，反之负小波与枯水位对应。

（1）小波系数实部

由图2小波系数实部图中可分析，沂河年径流量存在明显的年际变化规律。随着伸缩尺度a的逐渐增大，呈现出不同尺度振荡小波变换部分被分离。由上及下显示出22～26年尺度、9～19年尺度以及3～8年尺度周期变化，周期中心分别为5年、13年、24年，为更明确表达周期变化，不同时间尺度下分析。

从较大尺度24年分析，径流变化出现丰枯交替准四次振荡，沂河年径流变化出明显突变特征具体表现为1953年以前偏枯，1954～1958年偏丰，1958～1960年偏枯，1961～1974年偏丰，1975～1985年偏枯，1986～1991年偏丰，1992～2001年偏枯，2002～2010偏丰，直到2015年，等值线仍未闭合，2015年以后一段时间还将处于偏枯期。

13年尺度的周期变化具有局域性，主要在1951～1983年较活跃，具体表现为1953年以前偏丰，1954～1961年偏枯，1962～1969年偏丰，1970～1978年偏枯，1979～1983年偏丰，1983年后实部数值趋于负数，偏枯。

（2）小波系数模值

Morlet小波系数的模值表明不同时间尺度变化周期，所对应的能量密度在时间域中分布的反映，系数模值愈大，表明其所对应时段或尺度的周期性就愈强。如图3所示：9～19年时间尺度模值最大，但1983年之后模值小余10，说明在此时段内9～19年时间尺度的周期变化并不显著，这也相应于小波变换实部图13年时间尺度分析结果。

（3）小波方差

通过小波方差进行检验，利用计算公式（5），计算不同时间尺度对应的小波方差，以此来确定径流时间序列存在的主要周期。如图4所示：图中出现第一峰值是24年尺度对应的小波方差，说明24年左右的周期振荡最为明显，为第1主周期，第2、3周期依次为13年、5年。

四、结语

（1）本文针对临沂站沂河1951～2015年径流量，选用Morlet小波变换，获取了不同时间尺度变化及分布和突变点。发现沂河年径流量变化存在多时间尺度的特征，具有22～26年尺度、9～19年尺度以及3～8年的周期变化，周期中心24年、13年、5年，大尺度的周期变化中嵌套着小尺度的周期变化。

（2）本文对沂河流域1951～2015年的水文时间序列进行径流演变分析表明，该时段径流量总体呈下降趋势，通过小波分析,揭示出未来一段时间沂河还将处于枯水阶段，协调水资源调度，合理优化流域水资源配置迫在眉睫

（作者单位：1.刘家道口水利枢纽管理局 276000 2.淮河工程集团有限公司 221000）