基于RBF神经网络的SCR脱硝系统喷氨优化
廖永进, 范军辉, 杨维结, 季 鹏, 张 静, 冯永新
(1.广东电网有限责任公司电力科学研究院,广州 510080;2.华北电力大学 能源动力与机械工程学院,河北保定 071003)
基于RBF神经网络的SCR脱硝系统喷氨优化
廖永进1, 范军辉2, 杨维结2, 季 鹏2, 张 静2, 冯永新1
(1.广东电网有限责任公司电力科学研究院,广州 510080;2.华北电力大学 能源动力与机械工程学院,河北保定 071003)
为实现对电厂选择性催化还原(SCR)脱硝装置喷氨的优化控制,以广东某电厂350 MW锅炉为研究对象,采用径向基函数(RBF)神经网络法,以锅炉负荷、烟气体积流量、SCR烟气温度、脱硝进口NOx质量浓度以及喷氨质量流量等为输入变量,以SCR脱硝效率为输出变量,建立输入变量与输出变量之间的关系模型,实现对SCR脱硝效率及脱硝出口NOx质量浓度的预测.在满足NOx排放标准的前提下,以SCR系统运行成本最小为目标,利用Matlab对该模型进行仿真实验,寻求氨耗成本和电耗成本与NOx排放费用的临界点,得到最佳喷氨质量流量.结果表明:最佳喷氨质量流量计算值比实测值或高或低,但在满足NOx排放标准的前提下,其SCR系统运行成本呈降低趋势.
SCR; 喷氨质量流量; NOx排放; 脱硝效率; 成本
随着社会经济发展进程的不断加快,我国NOx排放量不断增加,因此面临巨大的NOx减排压力.据中国环境监测总站提供的数据,2011年我国NOx排放量为2 404.3万t[1],其中工业NOx排放量为1 729.7万t,火电行业作为NOx排放的主要来源,在运行过程中产生的NOx占工业NOx排放量的一半以上.对此,环境保护部已实施了新的GB 13223—2011 《火电厂大气污染物排放标准》[2],并印发了《全面实施燃煤电厂超低排放和节能改造工作方案》,要求广东等重点地区率先实现超低排放改造,即在基准氧体积分数为6%的条件下,烟尘、SO2和NOx排放质量浓度分别不高于10 mg/m3、35 mg/m3和50 mg/m3[3].
随着环保部门对NOx排放量限制的日益严格,低NOx燃烧技术和烟气脱硝技术被普遍应用于燃煤电站.选择性催化还原(SCR)法在国内燃煤电站中的应用最为广泛,具有脱硝效率高、技术成熟等优点[4-5].SCR法是指在催化剂、氧气和一定温度范围条件下,还原剂(一般为氨)有选择地将烟气中的NOx(主要是NO)还原生成N2和H2O.影响SCR脱硝效率的主要因素有烟气体积流量、SCR烟气温度、脱硝进口NOx质量浓度、喷氨质量流量以及催化剂活性等.根据实际运行情况来看,SCR烟气温度与锅炉负荷和燃料燃烧情况有关,催化剂通常只能在失效后更换,因而喷氨质量流量成为可日常调整的关键因素之一[6].喷氨质量流量过小,难以保证达到NOx排放标准;喷氨质量流量过大,不仅造成NH3的浪费,而且在空气预热器中逃逸的NH3会与烟气中的SO3和H2O反应生成NH4HSO4,而NH4HSO4有黏性,长时间堆积会引起堵灰现象[7-9].
尽管相关学者在优化控制喷氨方面进行了大量研究[10-15],包括自动控制喷氨装置的改进、喷氨方法的多样化、改变脱硝出口NOx质量浓度分布以及降低氨逃逸率等,但以SCR系统运行成本最小为目标来优化控制喷氨的研究较少.王桂林等[16]基于支持向量机法建立了锅炉运行过程中NOx生成和SCR脱硝效率的预测模型,以SCR系统运行成本最小为目标,利用遗传算法对喷氨质量流量进行优化,实现了对喷氨的优化控制.但对于不同炉型,喷氨的优化控制存在差异,且该模型预测误差相对较大.RBF神经网络法已经被证明具有很强的非线性映射能力[17],笔者以广东某电厂350 MW锅炉为研究对象,采用RBF神经网络法建立SCR脱硝效率预测模型;以SCR系统运行成本最小为目标,利用Matlab对该模型进行仿真实验,在满足NOx排放标准的前提下获得最佳喷氨质量流量.
1 研究对象及方法
1.1研究对象概况
广东某电厂350 MW供热抽汽凝汽式燃煤机组锅炉是武汉锅炉股份有限公司(AWBC)生产的亚临界参数、自然循环、一次中间再热、单炉膛平衡通风、固态排渣、露天布置、全钢构架的∏型汽包炉,已安装脱硝装置,设计煤种为石圪台煤,校核煤种1为神华混煤,参数如表1所示.采用SCR法,脱硝装置按2+1层布置,设计脱硝效率不低于80%.SCR脱硝装置催化剂采用蜂窝式催化剂,其主要参数如表2所示,脱硝系统进口烟气设计值见表3.
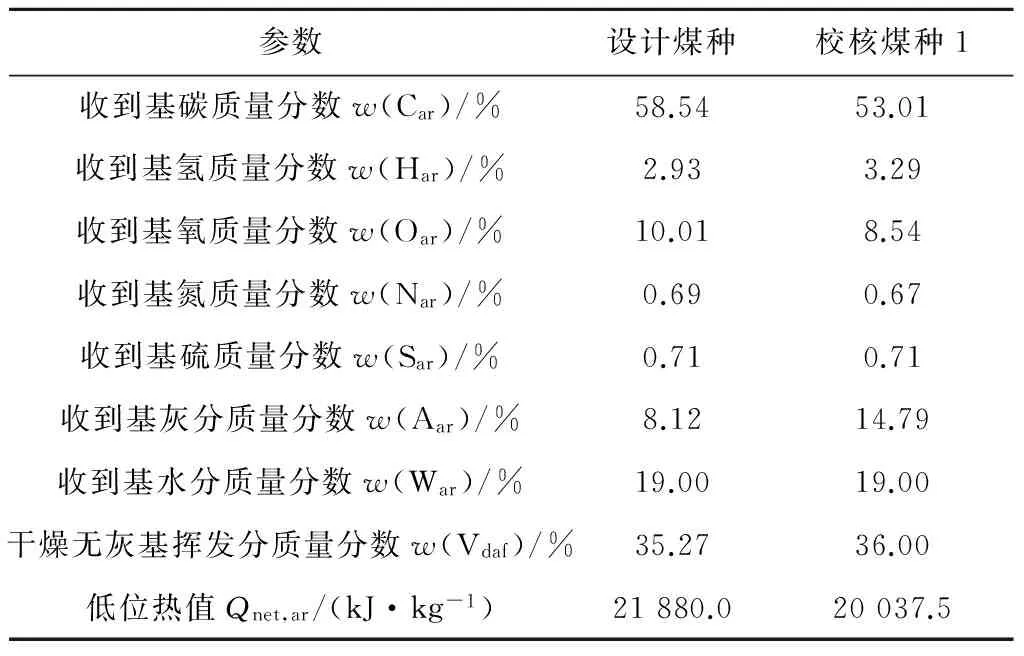
表1 煤质分析

表2 催化剂主要参数
表3脱硝系统进口烟气设计值(6%φ(O2)、标态、干基)
Tab.3Designparametersofinletfluegasinthedenitrificationsystem(6%φ(O2),standardstate,drybasis)

参数数值飞灰质量浓度/(g·m-3)36NOx质量浓度/(mg·m-3)400(设计值)SO2质量浓度/(mg·m-3)3150SO3质量浓度/(mg·m-3)38
1.2研究方法
笔者采用该机组的历史运行数据,利用RBF神经网络法建立SCR脱硝效率预测模型,预测出机组SCR脱硝效率以及脱硝出口NOx质量浓度,从而预测SCR系统运行成本.以SCR系统运行成本最小为目标,建立SCR系统运行成本关于喷氨质量流量的目标函数,利用Matlab对该模型进行仿真实验,得到在满足NOx排放标准前提下的最佳喷氨质量流量,实现对电厂SCR脱硝装置喷氨质量流量的优化控制.
1.2.1 RBF神经网络
RBF神经网络基于正则化理论导出,具有收敛速度快、可逼近任意非线性函数等优点.其网格结构简单,是一种3层前向网络,第1层为输入层,结点个数等于输入的维数;第2层为隐含层,结点个数视问题复杂度而定;第3层为输出层,结点个数为输出层的维数,如图1所示.RBF神经网络结构属于一种前馈网络的拓扑结构,其输入样本向量先与权值向量相乘,再输入到隐含层的节点,计算样本与节点中心的距离,该距离经过径向基函数的映射后形成隐含层输出,再输入到输出层,各个隐含层节点(以下简称隐节点)的线性组合形成了最终的网格输出[18].
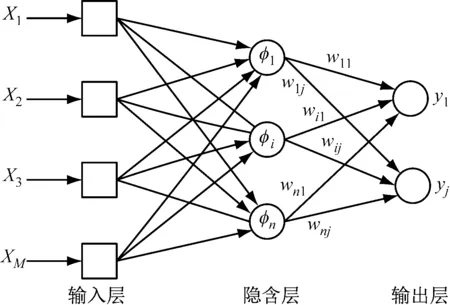
图1 RBF神经网络结构Fig.1 RBF neural network architecture
RBF神经网络从输入空间到隐含空间的变换是非线性的,而从隐含空间到输出空间的变换是线性的.在实现RBF神经网络由输入到输出的过程中,需要确定的主要参数为隐节点的中心及其标准差σ、径向基函数的宽度、隐含层与输出层间的权值矩阵.通常隐节点的中心可以采用聚类方法确定或直接从输入样本中选择,而标准差σ可通过式(1)求得,隐含层与输出层间的权值矩阵可通过求伪逆的方法得到.径向基函数的宽度决定隐节点对外部输入信号的相应范围,当输入信号靠近某个隐节点中心时,则该节点被激活,该节点将产生较大输出;当输入信号远离此隐节点中心时,则该隐节点的输出趋于0.径向基函数仅对输入信号产生局部响应,隐含层输出在输出层进行线性加权,实现从输入空间到输出空间的映射,从而使整个网络达到分类或函数逼近的目的[17].
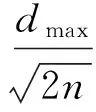
(1)
式中:dmax为选取隐节点中心之间的最大距离;n为隐节点个数,由OLS算法根据训练样本确定.
径向基网络与多层感知器不同,其隐含层为非线性,采用高斯函数作为径向基函数.径向基函数是一种局部分布的沿隐节点中心径向对称衰减的非负非线性函数,可用式(2)表示:
(2)
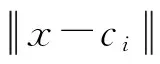
φi越小,说明径向基函数的宽度越小,基函数的选择性越强.网络的第k个输出可表示为:
(3)
式中:wki为隐含层神经元和输出层神经元之间的权值矩阵;yk为实际输出.
在应用RBF神经网络的过程中,先确定所有隐节点中心ci,然后校正隐含层神经元与输出层神经元之间的权值矩阵wki.
1.2.2 SCR系统运行成本计算
SCR系统运行成本包括氨耗成本、电耗成本、NOx排放费用、污染物排放达到标准后的电价补偿以及人工、折旧、维修等费用[19],其中污染物排放达到标准后的电价补偿以及人工、折旧、维修等费用固定,而氨耗成本、电耗成本以及NOx排放费用均与喷氨质量流量相关.
根据模型输入脱硝进口NOx质量浓度以及预测模型的SCR脱硝效率,计算脱除后NOx量,脱硝化学反应方程式为:

(4)

(5)
氨消耗质量流量qm,a(kg/h)为:
qm,a=[qV×ρNO×17/(30×106)+
qV×ρNO2×17×2/(46×106)]×m
(6)
ρNO=ρR,NOx/(2.05×0.95×1.34)
(7)
ρNO2=0.05×ρC,NOx
(8)
m=η/100+γa(ρNO/30+2ρNO2/46)/22.4
(9)
式中:ρNO、ρNO2分别为进口烟气NO、NO2的质量浓度,mg/m3;ρR,NOx为脱硝进口NOx质量浓度;ρC,NOx为进口烟气NOx的质量浓度;m为氨与SCR进口NOx质量浓度比;γa为氨逃逸率;qV为烟气体积流量,m3/h;η为预测出的SCR脱硝效率.
结合氨水单价(3 000元/t)计算氨耗成本F1(元/h):
F1=3×qm,a
(10)
根据喷氨质量流量及各脱硝设备总电流的相关数据,拟合出喷氨质量流量与各脱硝设备总电流之间的关系.一般情况下,喷氨质量流量越大,设备耗电量越大,可根据简单的线性关系来拟合:
I=k×qm+b
(11)
式中:qm为喷氨质量流量;I为各脱硝设备总电流;k和b均为常数,可通过数据拟合得到.
根据喷氨质量流量估算出电耗成本,结合电价0.3元/(kW·h)计算电耗成本F2(元/h):
F2=1.73×6 000×I×0.83×0.3÷1 000
(12)
根据脱硝进口NOx质量浓度及预测出的SCR脱硝效率η,可计算未脱除的NOx质量浓度.根据广东省NOx排污费用征收标准,NOx排放费用为每当量2.4元,可计算排污费用F3(元/h).
未脱除的NOx质量浓度为:
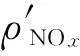
(13)
排污费用F3为:
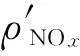
(14)
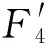
(15)
折合到单位时间,并统一单位,F4(元/h)可表示为:

(16)
式中:P为锅炉负荷.
其他成本包括人工、折旧、维修等费用,且基本固定,统一用G表示[20].将所有成本除以发电量,得到脱硝系统单位发电量总成本F(元·kW-1·h-1),F可表示为:
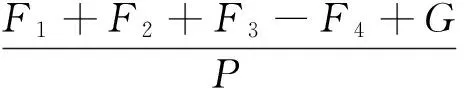
(17)
2 RBF神经网络SCR脱硝效率预测模型
2.1建立预测模型
选取锅炉负荷、烟气体积流量、SCR烟气温度、脱硝进口NOx质量浓度以及喷氨质量流量等为输入变量,以SCR脱硝效率为输出变量,构造一个5输入-1输出的预测模型,如图2所示.

图2 SCR脱硝效率η的预测模型Fig.2 Prediction model of the SCR denitrification efficiency η
根据预测模型的需要,随机选取100组数据作为训练样本(锅炉负荷在50%~100%内),25组数据作为测试样本,训练开始前先对数据进行滤波处理,筛除偏差较大的数据,然后利用Matlab神经网络工具箱提供的newrb函数对构造的网络模型进行训练.在训练过程中,由于newrb函数创建的径向基网络隐含层的节点不确定,因此根据设定的误差目标向径向基网络中不断添加新的隐节点,并调整节点中心、标准差及权值,直到网络达到预期的误差目标要求,设置误差容限为10-8.根据newrb函数创建的径向网络在Matlab中仿真,得到SCR脱硝效率训练误差,如图3所示.用view(net)命令得到最终的径向基网络结构,结构图显示隐含层包含198个神经元,如图4所示.

图3 训练误差曲线Fig.3 Training error curve
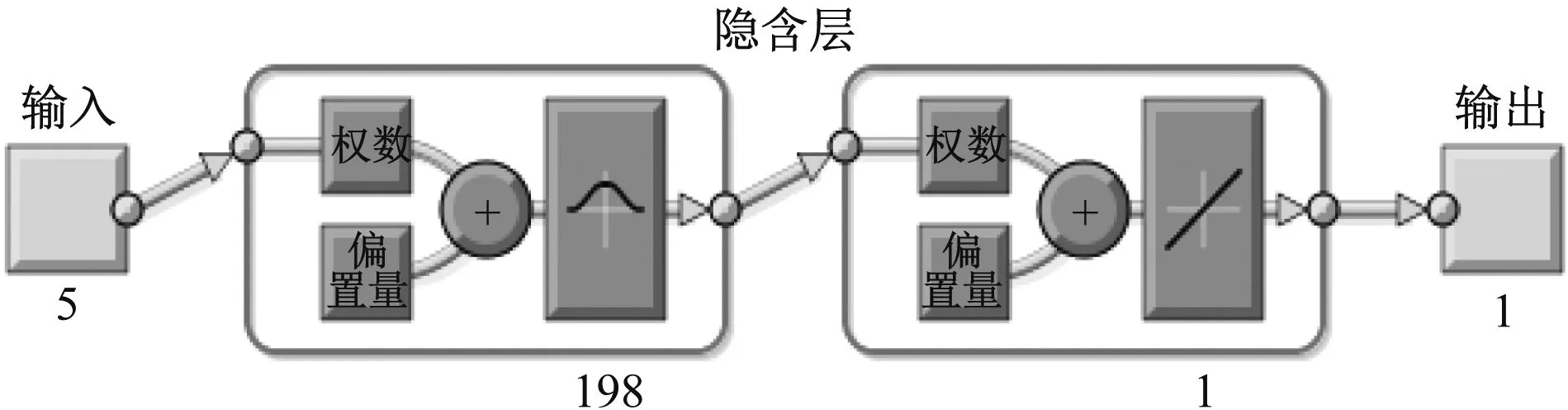
图4 建立的RBF网络结构图Fig.4 Establishment of the RBF network structure
2.2预测模型验证
为验证模型的准确性,对选取的25个样本进行预测,结果如图5所示.由图5可以看出,预测值与真实值非常接近,且两者的变化趋势完全一致.从相对误差的角度来看,100份测试样本的平均相对误差接近0.8%,最大相对误差接近4.8%,验证了采用RBF神经网络建立SCR脱硝效率预测模型的准确性,并可根据预测模型结果计算SCR系统运行成本.
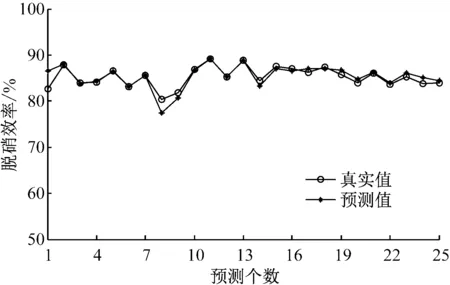
图5 SCR脱硝效率真实值与预测值的对比Fig.5 Comparison of denitrification efficiency between actual measurements and predicted results
3 喷氨优化控制
3.1SCR系统运行成本与喷氨质量流量的关系
稳定工况下锅炉负荷、烟气体积流量、SCR烟气温度、脱硝进口NOx质量浓度均为定值,喷氨质量流量为变量,式(9)的SCR脱硝效率可认为是关于喷氨质量流量的函数,即SCR系统运行成本是关于喷氨质量流量的函数.在满足NOx排放标准的前提下,以SCR系统运行成本最小为目标,利用Matlab对该模型进行仿真实验,寻求氨耗成本和电耗成本与NOx排放费用的临界点,得到最佳喷氨质量流量.
以如下工况为例计算最佳喷氨质量流量:锅炉负荷为330.9 MW,烟气体积流量为1 063.7 m3/h、SCR烟气温度为353 ℃、脱硝进口NOx质量浓度为317.3 mg/m3、喷氨质量流量为155.3 kg/h.根据建立的预测模型,SCR脱硝效率为81.6%,从而可计算SCR系统运行成本F.由于污染物排放达到标准后的电价补偿以及人工、折旧、维修等费用固定,因此仅需考虑氨耗成本、电耗成本以及NOx排放费用.根据式(17)可得到F′,其中F1=3qm,a,F2=2.54qm,a-155.9,F3=816.9-4.31qm,a,则F′可表示为:
F′=(1.23qm,a+661)/P
(18)
由式(18)可以看出,SCR系统运行成本与喷氨质量流量呈正相关,因此降低喷氨质量流量,可减小SCR系统运行成本.但降低喷氨质量流量直接导致SCR脱硝效率降低,使得脱硝出口NOx质量浓度无法满足排放标准,且面临罚款.
3.2优化喷氨质量流量
以喷氨质量流量为自变量,以SCR系统运行成本最小为目标,同时满足NOx排放标准,利用Matlab对该模型进行仿真实验,计算出最佳喷氨质量流量为164.9 kg/h,优化前后SCR系统运行成本的对比如图6所示.
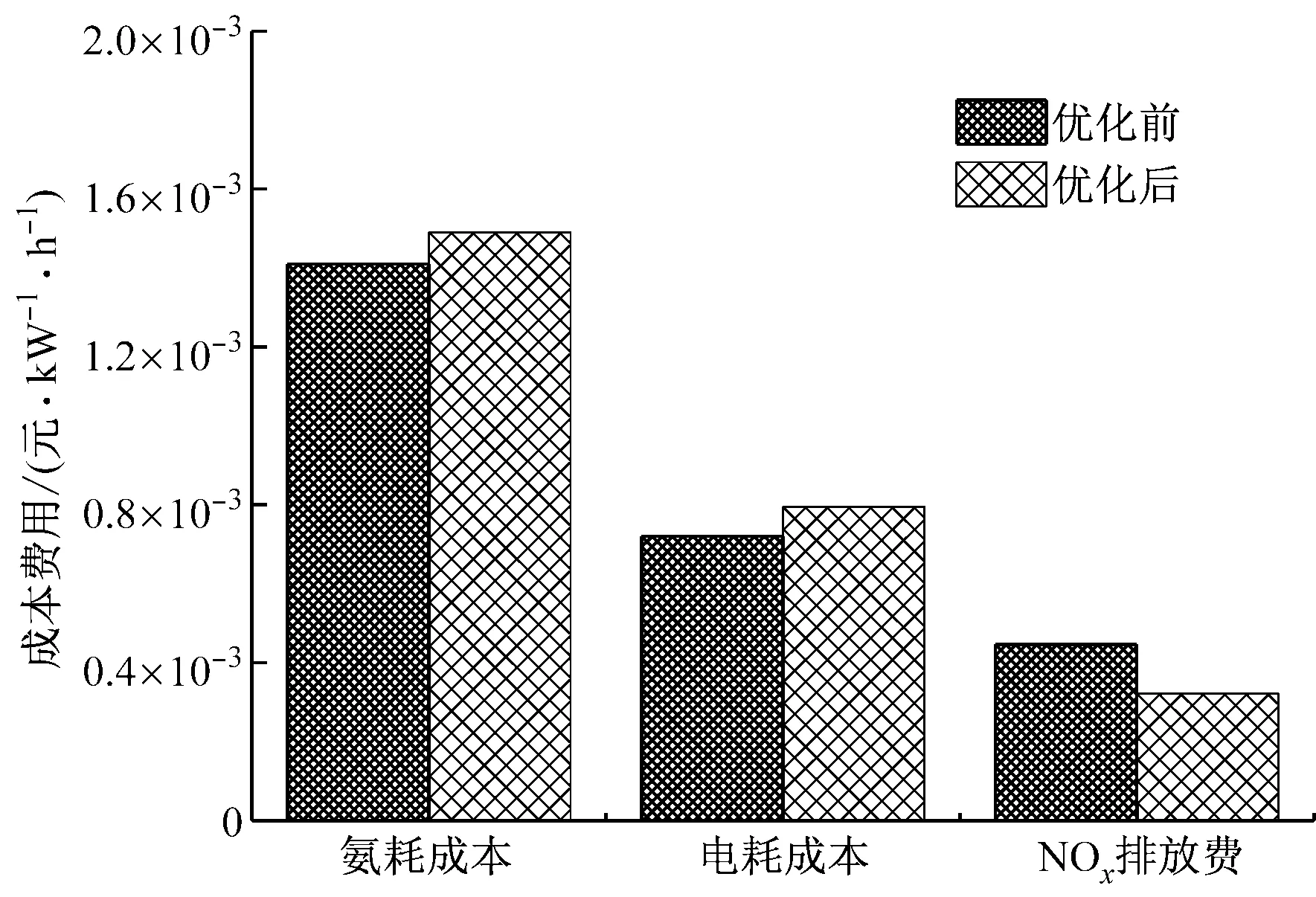
图6 优化前后各项SCR系统运行成本对比Fig.6 Operation cost of the SCR system before and after optimization
由图6可知,优化后氨耗成本比优化前上升了5.7%,电耗成本比优化前上升了约10.1%,而排污费用比优化前下降了约28.0%.通过对喷氨的优化控制,虽然氨耗成本和电耗成本的增加使得SCR系统运行成本F′略有上升,但NOx排放达到要求,且排污费用也会降低.
3.3不同工况下喷氨优化控制
计算不同工况下的最佳喷氨质量流量,结果如表4所示.由表4可知,8个工况下优化前后喷氨质量流量的变化有增有减,且变化幅度不一.当脱硝出口NOx质量流量不能满足排放标准时,需增加喷氨质量流量,使NOx的脱除量增加,虽然氨耗成本及电耗成本会增加,但NOx排放量减少,可降低排污费用;当SCR脱硝效率较高,在满足NOx排放的基础上可适当减小喷氨质量流量,降低SCR系统运行成本.因此,在满足排放标准的前提下,氨耗成本和电耗成本与NOx排放费用的临界点即为最小SCR系统运行成本对应的最佳喷氨质量流量.
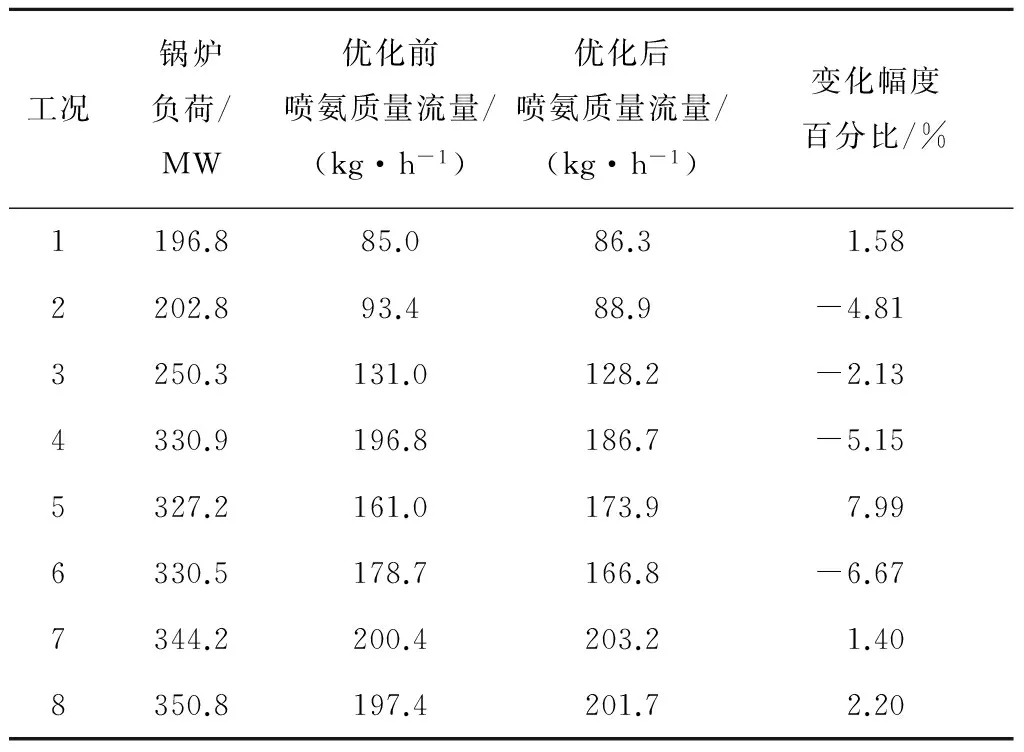
表4 不同工况下优化前后喷氨质量流量对比
4 结 论
(1)采用RBF神经网络的方法,以锅炉负荷、烟气体积流量、SCR烟气温度、脱硝进口NOx质量浓度以及喷氨质量流量等为输入变量,以SCR脱硝效率为输出变量,建立SCR脱硝效率预测模型,其误差在可接受范围内,说明预测值是可信的.
(2)在满足NOx排放标准的前提下,以SCR系统运行成本最小为目标,利用Matlab对该模型进行仿真实验,寻求氨耗成本和电耗成本与NOx排放费用的临界点,得到最佳喷氨质量流量.
(3)虽然最佳喷氨质量流量计算值比实测值或高或低,但在满足NOx排放标准的前提下,其SCR系统运行成本的趋势是降低的.
[1] 黄文静, 戴苏峰, 艾春美, 等. 电站燃煤锅炉全负荷SCR脱硝控制技术探讨[J].节能技术, 2015, 33(2): 189-192.
HUANG Wenjing, DAI Sufeng, AI Chunmei, et al. Discussion about SCR denitration control technology under full load in a coal-fired boiler[J].EnergyConservationTechnology, 2015, 33(2): 189-192.
[2] 中华人民共和国国家质量监督检验检疫总局. 火电厂大气污染物排放标准: GB 13223—2011[S]. 北京: 中国环境科学出版社, 2012.
[3] 中华人民共和国环境保护部.全面实施燃煤电厂超低排放和节能改造工作方案[R].北京:中华人民共和国环境保护部,2015.
[4] 顾卫荣, 周明吉, 马薇. 燃煤烟气脱硝技术的研究进展[J].化工进展, 2012, 31(9): 2084-2092.
GU Weirong, ZHOU Mingji, MA Wei. Technology status and analysis on coal-fired flue gas denitrification[J].ChemicalIndustryamp;EngineeringProgress, 2012, 31(9): 2084-2092.
[5] 秦胜, 张剑, 田莉雅. 火电厂氮氧化物控制技术探讨[J].能源环境保护, 2012, 26(4): 44-47.
QIN Sheng, ZHANG Jian, TIAN Liya. The controlling measures of nitrogen oxides in thermal power plants[J].EnergyEnvironmentalProtection, 2012, 26(4): 44-47.
[6] 周洪煜, 张振华, 张军, 等. 超临界锅炉烟气脱硝喷氨量混结构-径向基函数神经网络最优控制[J].中国电机工程学报, 2011, 31(5): 108-113.
ZHOU Hongyi, ZHANG Zhenhua, ZHANG Jun, et al. Mixed structure-radial basis function neural network optimal control on spraying ammonia flow for supercritical boiler flue gas denitrification[J].ProceedingsoftheCSEE, 2011, 31(5): 108-113.
[7] 杨建国, 樊立安, 赵虹, 等. 提高催化剂反应效率的烟温协调优化控制[J].中国电机工程学报, 2014, 34(14): 2244-2250.
YANG Jianguo, FAN Li'an, ZHAO Hong, et al. Coordinated optimization control of flue gas temperature for improving reaction efficiency of catalyst[J].ProceedingsoftheCSEE, 2014, 34(14): 2244-2250.
[8] 方朝君, 金理鹏, 余美玲. SCR脱硝喷氨优化与运行控制研究[J].电力科技与环保, 2015, 31(6): 39-42.
FANG Zhaojun, JIN Lipeng, YU Meiling. Research on optimization adjustment for ammonia injection and operation of SCR denitrification system in coal-fired power plant[J].ElectricPowerEnvironmentalProtection, 2015, 31(6): 39-42.
[9] 马双忱, 邓悦, 吴文龙, 等. SCR脱硝过程中硫酸氢铵形成特性实验研究[J].动力工程学报, 2016, 36(2): 143-150.
MA Shuangchen, DENG Yue, WU Wenlong, et al. Experimental research on ABS formation characteristics in SCR denitrification process[J].JournalofChineseSocietyofPowerEngineering, 2016, 36(2): 143-150.
[10] 周洪煜, 赵乾, 张振华, 等. 烟气脱硝喷氨量SA-RBF神经网络最优控制[J].控制工程, 2012, 19(6): 947-951.
ZHOU Hongyi, ZHAO Qian, ZHANG Zhenhua, et al. Sensitivity analysis radial basis function neural network control on spraying ammonia flow denitrification[J].ControlEngineeringofChina, 2012, 19(6): 947-951.
[11] 罗子湛, 孟立新. 燃煤电站SCR烟气脱硝喷氨自动控制方式优化[J].电站系统工程, 2010, 26(4): 59-60, 63.
LUO Zizhan, MENG Lixin. Ammonia flow automatic control mode optimization of SCR flue gas DeNOxfor coal-fired power plant[J].PowerSystemEngineering, 2010, 26(4): 59-60, 63.
[12] 周英贵, 金保昇. 基于非均匀入口条件的SCR氨喷射方法[J].华中科技大学学报(自然科学版), 2016, 44(4): 121-126.
ZHOU Yinggui, JIN Baosheng. Ammonia injection method for SCR based on non-uniform inlet condition[J].JournalofHuazhongUniversityofScienceandTechnology(NaturalScienceEdition), 2016, 44(4): 121-126.
[13] 赵大周, 王传奇, 司风琪, 等. 多变截面选择性催化还原系统喷氨方式数值模拟[J].热力发电, 2015, 44(12): 93-97.
ZHAO Dazhou, WANG Chuanqi, SI Fengqi, et al. Optimization of ammonia injection in a SCR denitration system with multiple variable cross sections: numerical simulation[J].ThermalPowerGeneration, 2015, 44(12): 93-97.
[14] 刘晓敏. 烟气脱硝SCR装置喷氨优化研究[J].热力发电, 2012, 41(7): 81-83.
LIU Xiaomin. Optimization of ammonia injection for SCR equipment[J].ThermalPowerGeneration, 2012, 41(7): 81-83.
[15] 曹志勇, 谭城军, 李建中, 等. 燃煤锅炉SCR烟气脱硝系统喷氨优化调整试验[J].中国电力, 2011, 44(11): 55-58.
CAO Zhiyong, TAN Chengjun, LI Jianzhong, et al. Experiment of optimization adjustment for ammonia injection of selective catalytic reduction flue gas denitration system in coal-fired boiler[J].ElectricPower, 2011, 44(11): 55-58.
[16] 王桂林, 张宇, 王森, 等. 基于支持向量机的选择性催化还原脱硝系统运行优化[J].环境工程学报, 2015, 9(10): 5011-5016.
WANG Guilin, ZHANG Yu, WANG Sen, et al. Operation optimization of selective catalytic reduction system based on support vector machine[J].ChineseJournalofEnvironmentalEngineering, 2015, 9(10): 5011-5016.
[17] 宋清昆, 李源松. RBF神经网络锅炉燃烧系统建模[J].哈尔滨理工大学学报, 2016, 21(1): 89-92.
SONG Qingkun, LI Yuansong. Modeling of the boiler combustion system by RBF neural networks[J].JournalofHarbinUniversityofScienceandTechnology, 2016, 21(1): 89-92.
[18] 陈明. MATLAB神经网络原理与实例精解[M]. 北京: 清华大学出版社, 2013.
[19] 郭斌, 廖宏楷, 徐程宏, 等. 我国SCR脱硝成本分析及脱硝电价政策探讨[J].热能动力工程, 2010, 25(4): 437-440.
GUO Bin, LIAO Hongkai, XU Chenghong, et al. Analysis of the SCR (selective catalytic reduction)-based denitration cost in China and exploratory study of its policies on denitration electricity price[J].JournalofEngineeringforThermalEnergyandPower, 2010, 25(4): 437-440.
[20] 霍秋宝, 田亮, 赵亮宇, 等. 火电机组不同脱硝方式下的运行费用分析[J].华北电力大学学报(自然科学版), 2012, 39(5): 87-92.
HUO Qiubao, TIAN Liang, ZHAO Liangyu, et al. Analysis of operation costs of thermal power units with different denitration methods[J].JournalofNorthChinaElectricPowerUniversity(NaturalScienceEdition), 2012, 39(5): 87-92.
AmmoniaSprayingOptimizationofanSCRDenitrificationSystemBasedonRBFNeuralNetwork
LIAOYongjin1,FANJunhui2,YANGWeijie2,JIPeng2,ZHANGJing2,FENGYongxin1
(1.Electric Power Research Institute of Guangdong Power Grid Corporation, Guangzhou 510080, China; 2. School of Energy and Power Engineering, North China Electric Power University, Baoding 071003, Hebei Province, China)
To optimize the control on ammonia spraying of the selective catalytic reduction (SCR) denitrification device in a 350 MW power boiler in Guangzhou, a relationship model was established between the input and output variables based on radial basis function (RBF) neural network by taking the boiler load, flue gas flow, SCR inlet flue gas temperature, SCR inlet NOxconcentration and the spraying ammonia flow as the input variables, and the SCR denitrification efficiency as the output variable, so as to realize the prediction of SCR denitrification efficiency and outlet NOxconcentration. Under the premise of satisfying the requirements of NOxemission and aiming at minimizing the operating cost of the SCR system, Matlab was used to perform a simulation experiment on the model to seek a critical point among the ammonia consumption cost, power consumption cost and the NOxemission fee, thus obtaining an optimal flow of spraying ammonia. Results show that the calculated mass flow of ammonia spraying is either higher or lower than the measurements, but the operating cost of the SCR system always keeps decreasing under the premise of meeting the NOxemission standard.
SCR; spraying ammonia flow; NOxemission; denitrification efficiency; cost
2016-07-06
2016-10-17
南方电网科研资助项目(K-GD2014-173)
廖永进(1971-),男,陕西西安人,高级工程师,硕士,研究方向为锅炉和烟气脱硫装置的调试、试验及优化.
电话(Tel.):13503098453;E-mail:lyj23455@163.com.
1674-7607(2017)11-0931-07
X701
A
610.30

