5 MW风力机地震工况塔架动力学响应研究
杨 阳, 李 春,2, 袁全勇
(1.上海理工大学 能源与动力工程学院,上海 200093;2.上海市动力工程多相流动与传热重点实验室,上海 200093)
5 MW风力机地震工况塔架动力学响应研究
杨 阳1, 李 春1,2, 袁全勇1
(1.上海理工大学 能源与动力工程学院,上海 200093;2.上海市动力工程多相流动与传热重点实验室,上海 200093)
基于FAST开源软件和Wolf土-构耦合(SSI)模型建立了风力机地震工况动力学仿真模型,并计算了5种不同平均风速的气动载荷与101种不同强度的地震载荷联合作用下风力机的动力学响应.结果表明:在额定风速下,气动载荷与地震载荷之间为非线性耦合,评估风力机地震动力学响应时,必须充分考虑风-震耦合效应;风速相同时,塔基最大弯矩先保持不变,再以线性增长的趋势变化;在低强度地震时,塔架不同高度处的最大弯矩与塔架高度之间为线性关系;随着地震强度的逐渐增大,塔架最大弯矩与塔架高度之间的关系逐渐变为非线性,且额定风速下塔架最大弯矩最大.
风力机; 地震载荷; 动力学响应; 架结构强度
我国风力资源相对丰富的地区为西北部和东南沿海地区,分别位于亚欧大陆地震带和环太平洋地震带,因此在该地区建立的风力机极易受到地震载荷影响.风力机运行环境为典型的非定常时域和非均匀空间风场,大型风力机在非稳定气动载荷作用下,叶片和塔架等细长柔性体的气动弹性响应具有强非线性的特点,时域动态响应具有明显的非平稳特征[1-4].如果同时受到地震载荷作用,风力机系统的平衡极易被破坏,尤其是塔架结构的稳定性难以保证[5].因此,有必要研究在气动载荷与地震载荷联合作用下塔架的动力学响应.
许多国内外学者针对地震载荷对风力机结构动力学响应的影响展开了相关研究.Bazeos等[6]和Lavassas等[7]均基于有限元法评估了在地震载荷作用下风力机钢建圆柱型塔架的结构强度,但是模型均忽略了风轮和机舱,未考虑气动载荷的影响.Witcher[8]利用GH Bladed软件,结合风轮气动载荷与地震载荷建立了风力机动力学仿真模型,并研究了地震加速度峰值为1.1 m/s2时地震载荷对2 MW风力机机舱位移动态响应的影响,发现停机工况与紧急停机工况下机舱的振动幅度明显大于正常运行工况下机舱的振动幅度,说明发生地震时气动载荷和风轮-机舱-塔架系统传动载荷对计算结果的影响很大.Asareh等[9-10]基于FAST开源软件建立了可考虑气动载荷与地震载荷联合作用的风力机动力学仿真平台Seismic,并将计算结果与著名地震工程仿真软件OpenSees的结果进行比较,验证了其计算结果的有效性.杨阳等[11]基于风力机多体动力学仿真FAST开源软件建立了湍流风与地震耦合(风-震耦合)的计算模型,将风力机基础平台与土地相互作用的耦合(土-构耦合)效应简化为具有一定刚度和阻尼系数的弹簧振子,并模拟了多组气动载荷与地震载荷联合作用下风力机的结构动态特性,发现地震载荷使得塔尖位移增大2倍以上,并加剧了结构的非平稳响应.以上研究仅分析了1种地震载荷下风力机的结构动力学响应,对设计塔架抗震结构的参考价值有限.
笔者以美国可再生能源实验室(NREL)发布的5 MW风力机为研究对象,基于FAST开源软件的预留数据接口,根据Wolf模型建立土-构耦合模型,将地震加速度谱转化为地震载荷,并与气动载荷联合作用于风力机系统.通过目标响应谱的方法生成101种不同强度的地震加速度谱,分别研究在低风速、额定风速和高风速下风力机塔尖和塔基的受载情况,为风力机塔架结构抗震设计提供参考.
1 地震动力学仿真模型
1.1FAST开源软件
FAST开源软件[12]是NREL开发的专用于风力机气动弹性计算及结构动力学仿真的软件,可计算风力机疲劳特性、非定常风轮气动载荷和结构动力学特性.通过Pitt-Peters-He动态入流理论求解风轮平面诱导速度,结合叶素-动量理论和Prandtl叶尖损失修正模型计算风轮气动载荷,采用Beddoes-Leishiman动态失速模型修正偏航及变桨时叶片的非定常气动载荷.通过Kane方法建立风力机系统的多体动力学模型,采用模态法计算叶片、塔架和低速轴等柔性结构的弹性变形.气动载荷及结构变形的计算方法具有很高的效率,可快速求解风力机的气动弹性效应和动力学响应,计算结果的精度获得了德国劳式船级社(GL)认证,具有较高的可靠性.
1.2塔架动力学模型
假设塔架为倒置悬臂梁结构,塔基为悬臂梁根部,塔架纵向和侧向位移相互独立[13].采用模态截断法和Kane方法建立塔架动力学模型.在t时刻塔架位移u(x,t)可通过N个形状函数线性叠加表示:
(1)
式中:φj(x)为形状函数;cj(t)为广义坐标;x为塔架与塔基的距离.
FAST开源软件中考虑了塔架前二阶的前后振动和侧向振动,通过式(1)可将连续的塔架振动简化为具有4个自由度的离散形式.采用拉格朗日方法建立系统的自由振动方程:
i=1,2,3,4
(2)
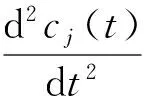
根据Thomson-Dahleh理论可给出系统的动能和势能,与式(2)合并可得广义质量和广义刚度:
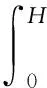
(3)
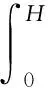
(4)
式中:g为重力加速度;φi(x)为第i个自由度的形状函数;mTop为塔架顶端质量,即风轮、机舱和偏航装置质量;E(x)和I(x)分别为塔架x高度处的弹性模量和惯性矩;ρ(x)为塔架x高度处的密度;H为塔架高度.
塔架每一阶模态φi(x)均可通过形状函数叠加来表示:
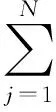
(5)
式中:Cij为构成第i阶模态的第j个形状函数φj(x)对应的广义坐标.
FAST开源软件中考虑了塔架4阶模态,则塔架位移u(x,t)可表示为:
φi(x)
(6)
式中:qi(t)为构成塔架位移的第i阶模态对应的广义坐标.
假设塔架以i阶模态φi(x)振动,相应的广义坐标解为正弦函数形式,即qi(t)=Aisin(ωit+ψi),其中Ai为正弦函数的幅值,ωi为频率,ψi为相位.则形状函数对应的广义坐标可表示为:
cj(t)=qi(t)Cij,j=1,2,…,N
(7)
将式(7)代入式(2)并表示为矩阵形式:
(-ω2M+K)C=0
(8)
式中:M为广义质量矩阵;K为广义刚度矩阵;C为系数向量;ω为塔架固有频率.
式(8)即为矩阵M-1K的特征值问题,求解后可得塔架的自振频率和各阶模态的参与系数.根据模态法建立前4阶模态的塔架动力学模型,即通过式(6)得到塔架位移,从而得到塔架强迫振动方程:

(9)
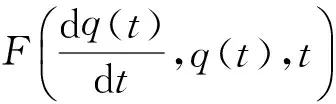
采用Runge-Kutta法求解式(9),即可获得塔架的结构位移和速度.
1.3土-构耦合模型
风力机基础平台与土地之间的耦合作用可通过Wolf模型进行描述,采用具有一定刚度K和阻尼系数C的弹簧振子表示土-构耦合,如图1所示.
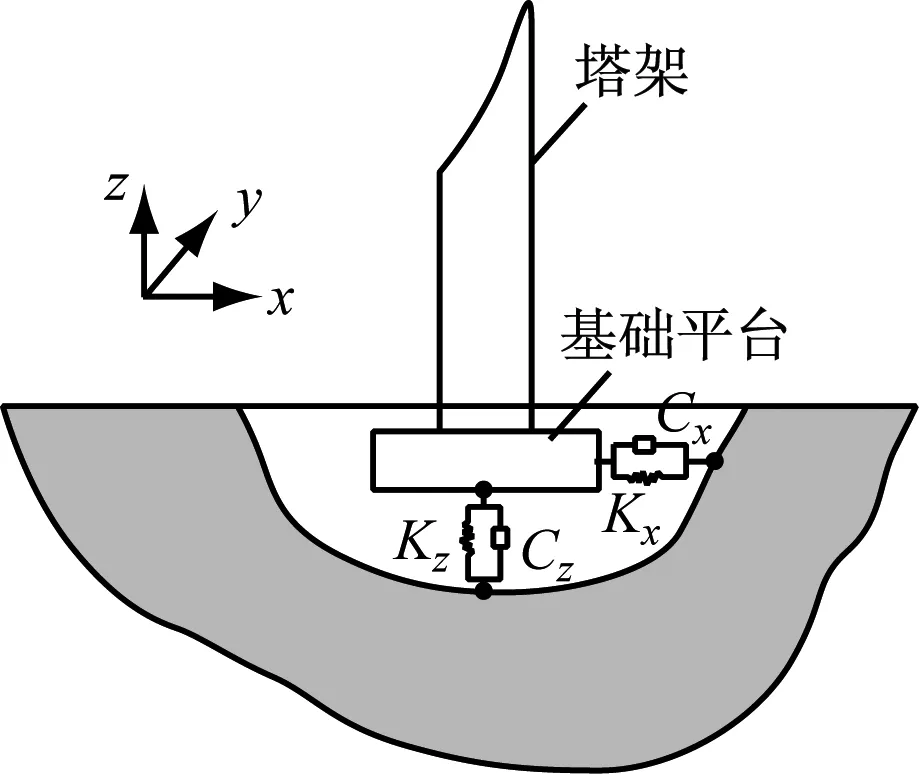
图1 土-构耦合模型Fig.1 Soil-structure interaction model
通过式(10)、式(11)计算各方向的刚度K和阻尼系数C:

(10)
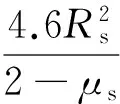
(11)
式中:下标x和y表示水平方向,z表示垂直方向;Gs、μs和ρs分别为土地的切变模量、泊松比和密度,分别取值为5.5 MPa、0.333和2 700 kg/m3;Rs为基础平台的半径.
1.4地震加速度谱及地震载荷计算
采用匹配目标谱的方法计算地震加速度[14],任一目标谱的表示方法如图2所示.图中Sa(t)为目标谱;ag为设计加速度峰值;TB、TC均为加速度周期常数范围限值参数;TD为位移周期常数值;q为性能参数,表示结构延性,取值为1;η为阻尼修正系数,η=[10/(5+ξ)]0.5,其值应大于0.55,一般取值为1,此时黏性阻尼百分比ξ为5%.
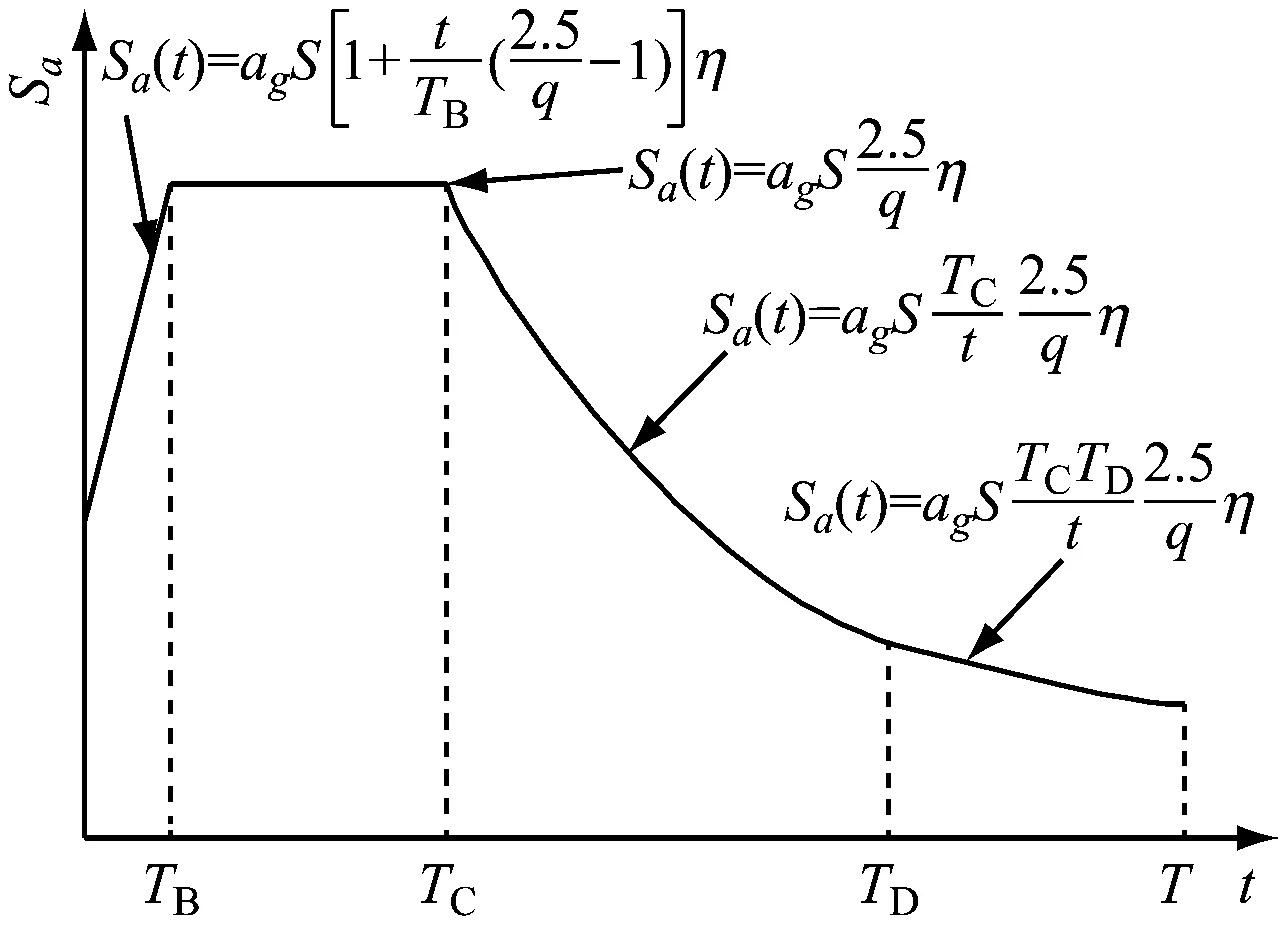
图2 目标谱示意图Fig.2 Schematic diagram of the target spectrum
选择1979年美国帝王谷(Imperial Valley)实测地震谱为目标谱,共计算101种不同强度的地震加速度谱ag,其变化范围为0.02~12.589 m/s2,每种地震时长为50 s.图3给出了ag分别为10.2 m/s2(工况1)、7.0 m/s2(工况2)和3.8 m/s2(工况3)时x方向的加速度目标谱匹配以及时域变化情况,y方向和z方向的变化情况与x方向相似.
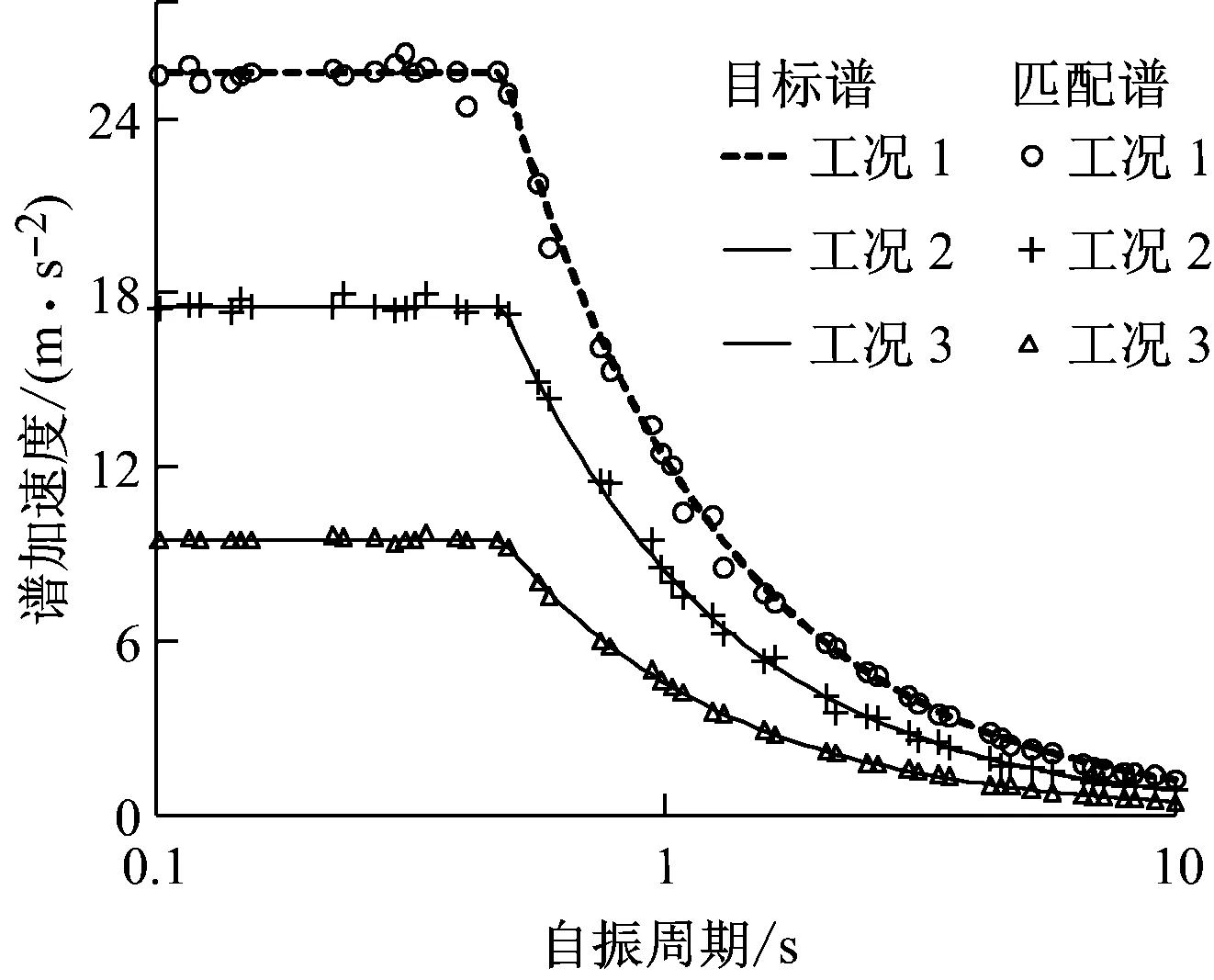
(a) 地震加速度目标谱匹配情况
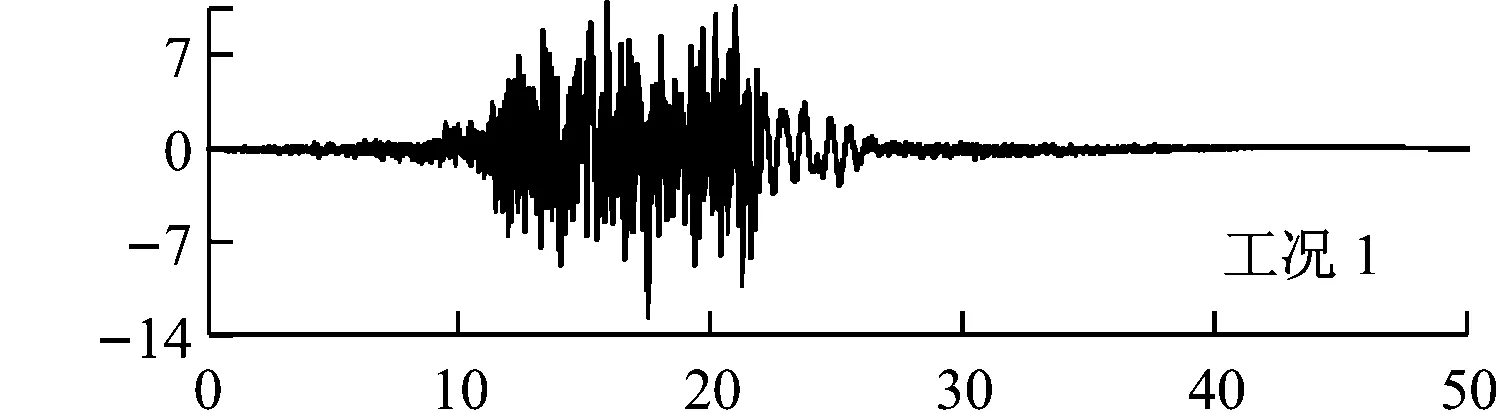
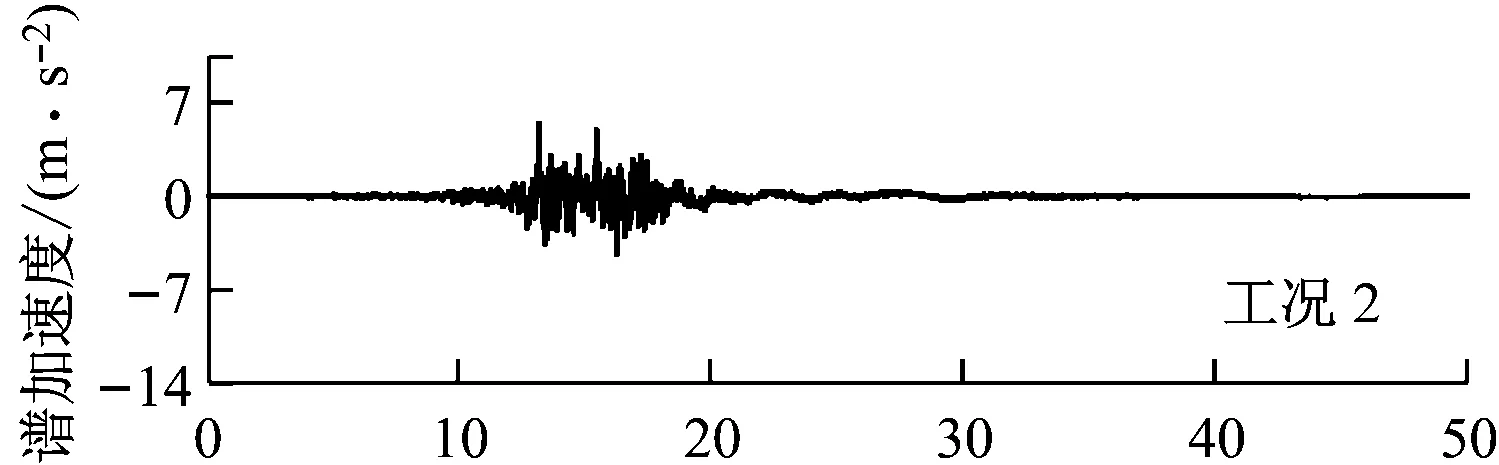
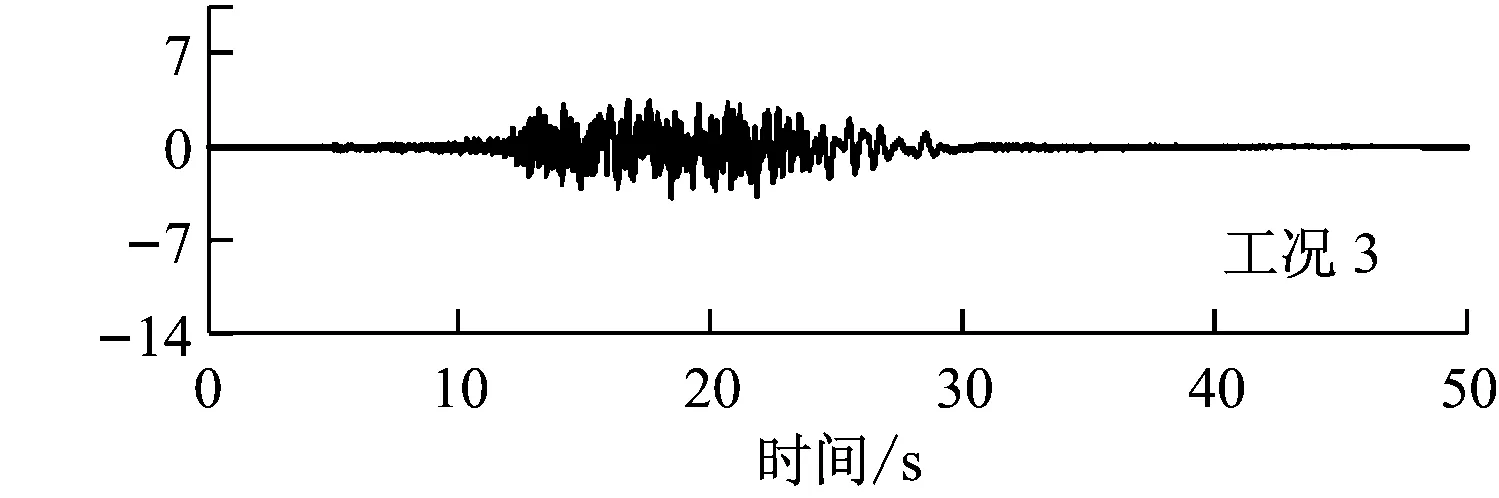
(b) 地震加速度的时域变化图3 x方向上不同强度的地震加速度目标谱匹配以及时域变化情况
Fig.3 Target spectrum, matched spectrum and acceleration of different intensity earthquakes inxdirection
当地震发生时,基础平台的目标加速度为地震加速度,基础平台γ方向的地震载荷Fγ为:
Fγ=-Kγ(dγ-dγ,t)-Cγ(Vγ-Vγ,t)
(12)
式中:dγ和Vγ分别为基础平台γ方向的实际位移和实际运动速度;dγ,t和Vγ,t分别为基础平台γ方向的目标位移和目标速度;γ表示方向(γ=x,y,z,见图1).
2 研究对象及计算工况
2.1研究对象
选取NREL 5 MW风力机为研究对象,其主要性能参数和结构参数如表1所示.
2.2计算工况
为研究气动载荷与地震载荷联合作用对风力机动力学响应的影响,分别计算平均风速为5 m/s、8 m/s、11.4 m/s、15 m/s和18 m/s时的湍流风速,并通过TurbSim[1]软件生成湍流风场.平均风速分别为5 m/s、11.4 m/s和18 m/s时轮毂高度处的风速时域变化情况如图4所示.由图4可以看出,风速具有明显的非定常时域特性.对于每种风速,均需考虑101种不同强度地震载荷与气动载荷的耦合作用.笔者共计算505个算例,每1个算例的仿真时间为600 s,时间步长为0.005 s.假设地震在400 s时发生,可以保证在地震载荷加入前风力机系统响应与气动载荷之间已经处于动态平衡状态,地震运动持续时间为50 s.
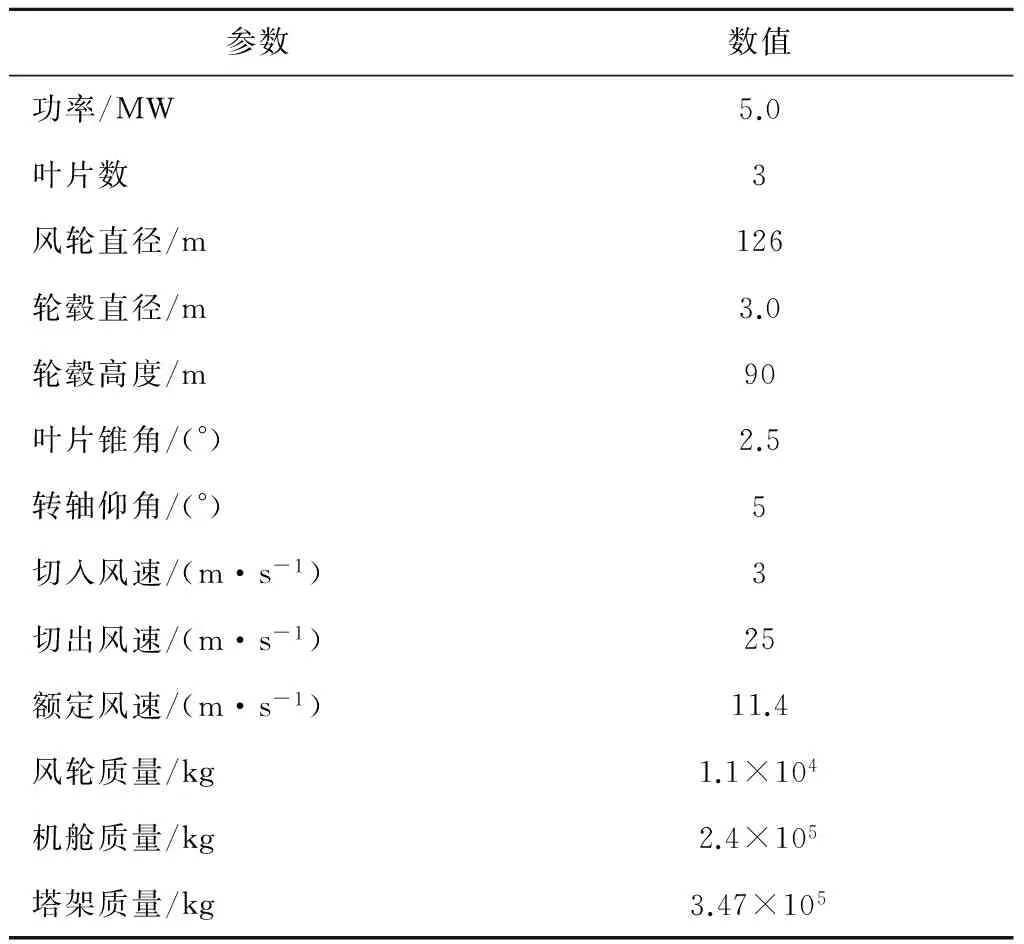
表1 NREL 5 MW风力机主要参数

图4 不同平均风速下轮毂高度处的风速时域变化
Fig.4 Wind speed changes at hub height in time domain under different wind conditions
3 结果分析
3.1风-震耦合效应
为分析风-震耦合效应,分别给出了地震发生时间段内(400~450 s)气动载荷或地震载荷单独作用时塔架的动力学响应情况(见图5).图6为考虑风-震耦合效应以及气动载荷与地震载荷线性叠加这2种情况下塔架的弯矩响应对比.气动载荷环境是平均风速为11.4 m/s的湍流风场,地震载荷环境是地震加速度峰值为4.7 m/s2的地震运动.由图5可以看出,气动载荷单独作用时塔顶总弯矩响应波动范围为4~6 MN·m,其平均值远大于地震载荷单独作用时塔顶总弯矩的响应平均值,但两者的响应峰值相差较小.塔基与塔顶的总弯矩响应类似,地震载荷单独作用时,其响应峰值略大于气动载荷单独作用时.由图6可以看出,将2种载荷单独作用时的塔架弯矩响应值线性相加后,其数值明显大于2种载荷全耦合作用时的塔架弯矩响应值,说明风力机受到地震作用时,地震载荷与气动载荷之间为非线性耦合.进一步说明评估风力机地震动力学响应时,必须充分考虑风-震耦合效应.单独考虑气动载荷或地震载荷时,将塔架弯矩响应值线性相加会导致载荷评估趋于保守.针对所选算例,风-震耦合与未耦合情况下的塔顶弯矩最大值相差42%,塔基总弯矩最大值相差13%.

(a)
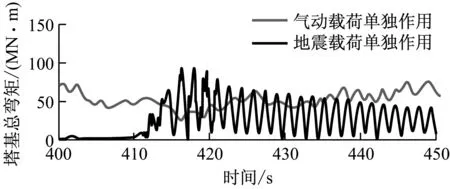
(b)图5 气动载荷或地震载荷单独作用时塔架弯矩的响应对比
Fig.5 Dynamic response of tower bending moment under independent action of aerodynamic load or seismic load
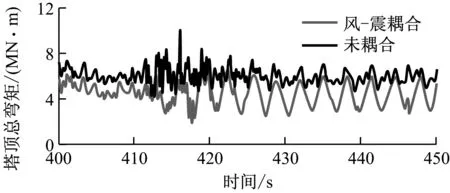
(a)
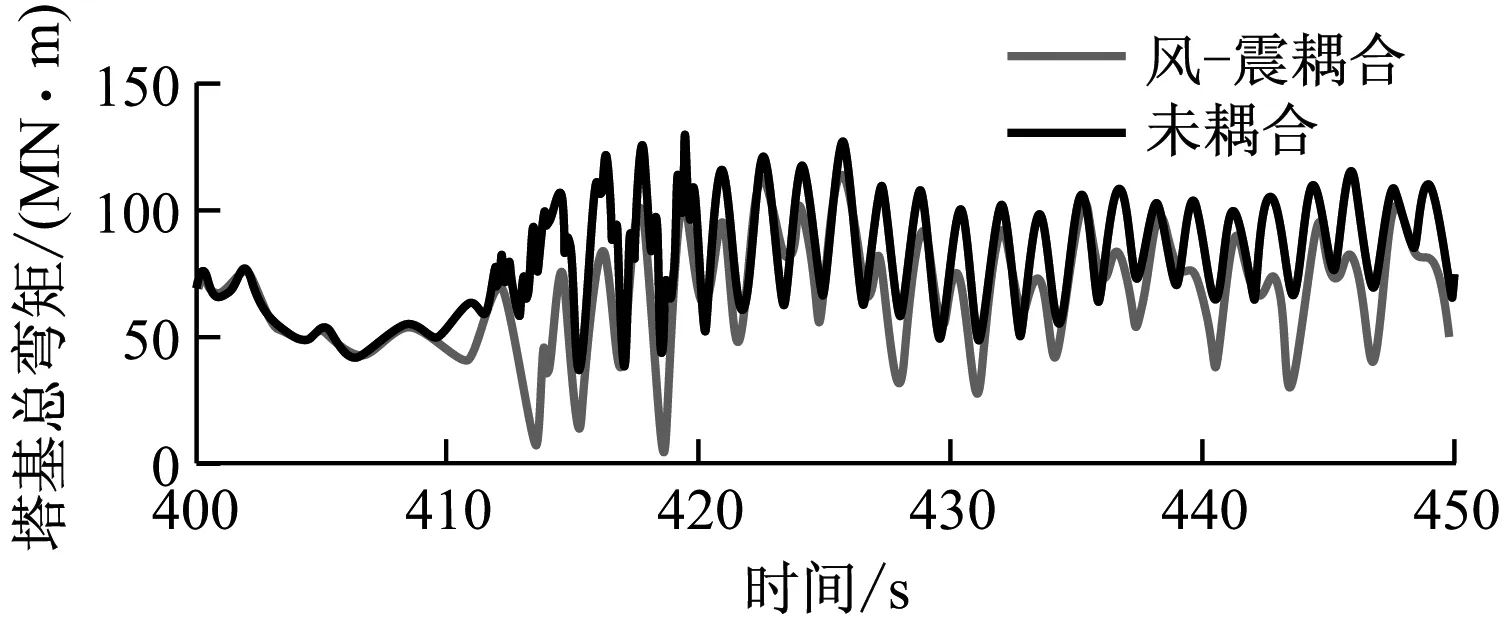
(b)图6 风-震耦合及未耦合情况下塔架弯矩的响应对比
Fig.6 Dynamic response of tower bending moment under coupled or uncoupled action of aerodynamic load and seismic load
3.2地震强度对塔基弯矩的影响
计算5种平均风速下不同地震强度的塔基弯矩响应值Mt,塔基最大弯矩Mt,max随地震加速度峰值(PGA)的变化趋势如图7所示.
由图7可以看出,随着PGA的增大,5种平均风速下Mt,max均为先保持不变,再逐渐增大.除额定风速外,其他风速下Mt,max均呈明显的线性增加.额定风速下,PGA为1.70~4.72 m/s2时Mt,max的增长规律为非线性;PGA大于4.72 m/s2时Mt,max的增长规律为近线性.主要原因是额定风速下气动载荷最大,风轮和塔架气动弹性响应最为明显,风力机系统气动阻尼变化最大.相比其他风速,气动载荷与地震载荷的耦合作用更为复杂,塔基弯矩时域动态变化的随机性更强,Mt,max随地震强度的变化规律与其他风速不同.随着PGA进一步增大,地震载荷对系统阻尼的贡献比例远大于气动载荷,塔基弯矩变化主要受地震载荷的影响,因此Mt,max与PGA存在明显的线性关系,额定风速与其他风速下Mt,max的变化规律相同.

图7 有无地震工况下塔基最大弯矩的动态响应对比
Fig.7 Dynamic response of tower top moment under normal and seismic conditions
3.3塔架动力学响应
PGA分别为1.08 m/s2、2.06 m/s2、3.03 m/s2、4.01 m/s2和4.99 m/s2时,不同平均风速下塔架不同高度处的最大弯矩如图8所示.
由图8可以看出,PGA为1.08 m/s2时塔架不同高度处的最大弯矩与塔架高度基本为线性关系.由于5 m/s风速下的气动载荷远小于其他风速下的气动载荷,在地震强度较低(PGAlt;3 m/s2)时其塔架最大弯矩远小于其他风速下的塔架最大弯矩.除风为11.4 m/s外,随着PGA增大,塔架不同高度处的最大弯矩与塔架高度之间的关系由线性逐渐变为非线性.11.4 m/s风速下塔架最大弯矩达到最大,说明进行风力机结构抗震设计时,可仅考虑额定风速下不同气动载荷与地震载荷的耦合效应对结构强度的影响.以地震加速度谱的变化规律为例,PGA为4.99 m/s2时地震强度(里氏震级)约为7.3级,塔基弯矩的设计需求为118 MN·m,IBC (International Building Code)建筑结构抗震标准规定安全系数为1.4,则5 MW风力机塔基弯矩的设计需求为165 MN·m.
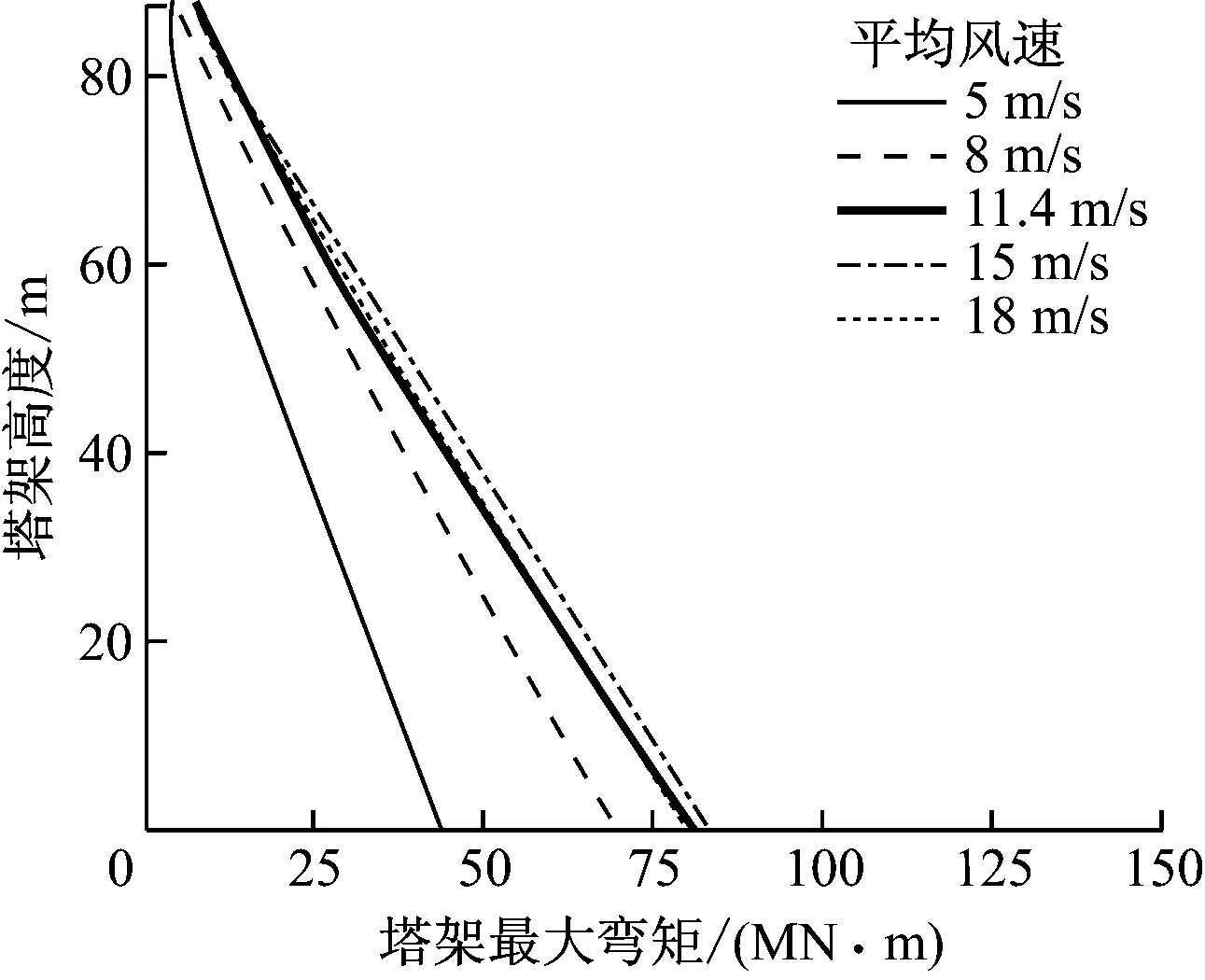
(a) PGA为1.08 m/s2
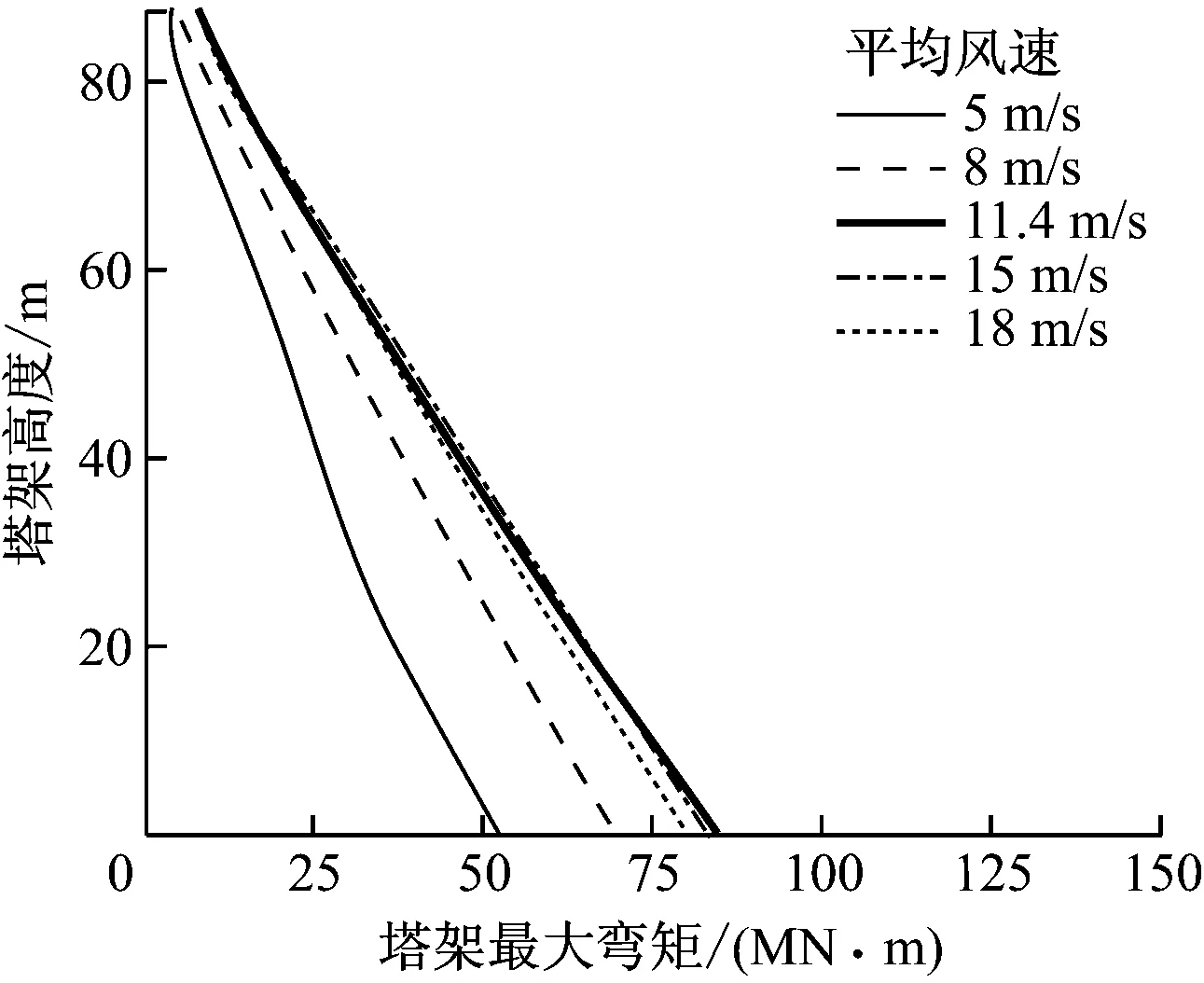
(b) PGA为2.06 m/s2
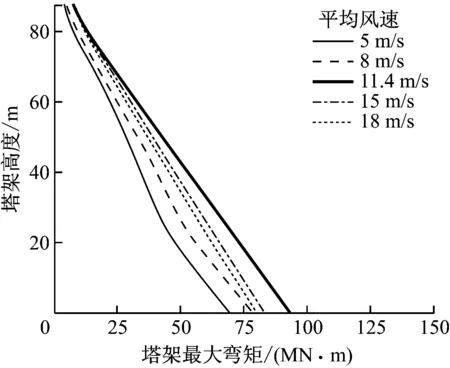
(c) PGA为3.03 m/s2
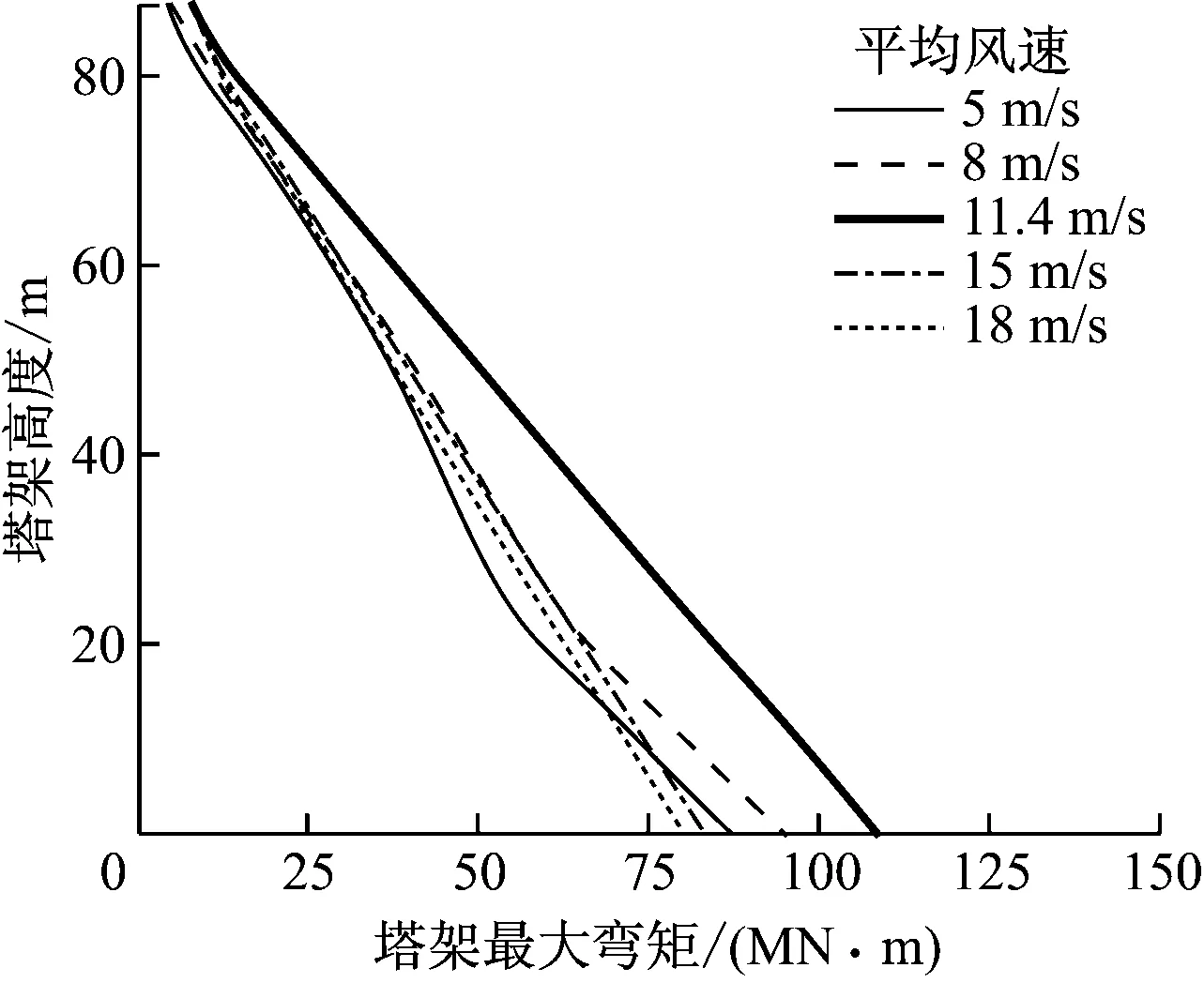
(d) PGA为4.01 m/s2
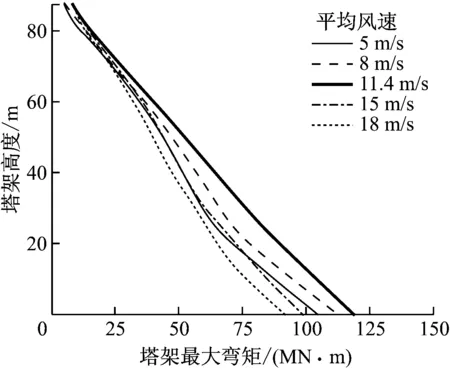
(e) PGA为4.99 m/s2图8 不同地震强度及风速下塔架不同高度处的最大弯矩Fig.8 Maximum bending moment at different elevations of tower under different seismic intensities and at different wind speeds
4 结 论
(1)额定风速下,风力机受到地震作用时气动载荷与地震载荷之间为非线性耦合.评估风力机的地震动力学响应时必须充分考虑风-震耦合效应.单独考虑气动载荷或地震载荷时,将塔架响应线性相加的结果会有一定的偏差.
(2)在同一风速下,随着地震强度的不断增大,塔基最大弯矩先保持不变,再以线性增长的趋势变化.额定风速下,气动阻尼与地震阻尼之间复杂的耦合作用对风力机系统动力学响应影响较大,塔基最大弯矩随地震强度的变化趋势呈近线性方式.
(3)在低地震强度时,塔架不同高度处的最大弯矩与塔架高度之间为线性关系.随着地震强度的增大,塔架最大弯矩与塔架高度之间的关系逐渐变为非线性,且额定风速下塔架最大弯矩达到最大.
[1] 吴攀, 李春, 李志敏, 等. 风力机不同风况的动力学响应研究[J].中国电机工程学报, 2014, 34(26): 4539-4545.
WU Pan, LI Chun, LI Zhimin, et al. Research on dynamic characteristics simulation for wind turbine with different wind[J].ProceedingsoftheCSEE, 2014, 34(26): 4539-4545.
[2] 杨阳, 李春, 缪维跑, 等. 高速强湍流风况下的风力机结构动力学响应[J].动力工程学报, 2016, 36(8): 638-644, 657.
YANG Yang, LI Chun, MIAO Weipao, et al. Structural dynamic response of a wind turbine under high-speed and strong turbulence inflow condition[J].JournalofChineseSocietyofPowerEngineering, 2016, 36(8): 638-644, 657.
[3] 杨阳, 李春, 叶柯华, 等. 基于HHT方法的非稳定工况风力机结构动态响应时频特性分析[J].振动与冲击, 2016, 35(21): 22-28.
YANG Yang, LI Chun, YE Kehua, et al. Analysis of structural dynamic response of wind turbine in time-frequency domain under non-stationary operating condition based on HHT method[J].JournalofVibrationandShock, 2016, 35(21): 22-28.
[4] 杨阳, 李春, 叶柯华, 等. 多工况下大型风力机动态响应研究[J].工程热物理学报, 2016, 37(10): 2123-2129.
YANG Yang, LI Chun, YE Kehua, et al. Research on dynamic response of large-scale wind turbine under multiple loading conditions[J].JournalofEngineeringThermophysics, 2016, 37(10): 2123-2129.
[5] 贺广零, 周勇, 李杰. 风力发电高塔系统地震动力响应分析[J].工程力学, 2009, 26(7): 72-77.
HE Guangling, ZHOU Yong, LI Jie. Seismic analysis of wind turbine system[J].EngineeringMechanics, 2009, 26(7): 72-77.
[6] BAZEOS N, HATZIGEORGIOU G D, HONDROS I D, et al. Static, seismic and stability analyses of a prototype wind turbine steel tower[J].EngineeringStructures, 2002, 24(8): 1015-1025.
[7] LAVASSAS I, NIKOLAIDIS G, ZERVAS P, et al. Analysis and design of the prototype of a steel 1-MW wind turbine tower[J].EngineeringStructures, 2003, 25(8): 1097-1106.
[8] WITCHER D. Seismic analysis of wind turbines in the time domain[J].WindEnergy, 2005, 8(1): 81-91.
[9] ASAREH M A, PROWELL I. Seismic loading for FAST[R]. USA: National Renewable Energy Laboratory, 2011.
[10] ASAREH M A, PROWELL I, VOLZ J, et al. A computational platform for considering the effects of aerodynamic and seismic load combination for utility scale horizontal axis wind turbines[J].EarthquakeEngineeringandEngineeringVibration, 2016, 15(1): 91-102.
[11] 杨阳, 李春, 缪维跑, 等. 湍流风场与地震激励联合作用下的风力机结构动力学响应[J].振动与冲击, 2015, 34(21): 136-143.
YANG Yang, LI Chun, MIAO Weipao, et al. Response of structural dynamic characteristics of wind turbine operating in turbulent wind combined with seismic motion[J].JournalofVibrationandShock, 2015, 34(21): 136-143.
[12] JONKMAN J M, BUHL M L J. FAST user's guide[R]. USA: National Renewable Energy Laboratory, 2005.
[13] JONKMAN J M. Modeling of the uae wind turbine for refinement of FAST_AD[R]. USA: National Renewable Energy Laboratory, 2003.
[14] ATIK L A, ABRAHAMSON N. An improved method for nonstationary spectral matching[J].EarthquakeSpectra, 2010, 26(3): 601-617.
ResearchonDynamicResponseofa5MWWindTurbineTowerUnderSeismicConditions
YANGYang1,LIChun1,2,YUANQuanyong1
(1. School of Energy and Power Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China; 2. Shanghai Key Laboratory of Multiphase Flow and Heat Transfer in Power Engineering, Shanghai 200093, China)
A dynamic simulation model was established for wind turbine on the basis of FAST open source software and Wolf soil-structure interaction (SSI) model under seismic conditions, with which the structural dynamic response of wind turbine was calculated under the combined action of aerodynamic loads at 5 mean wind speeds and seismic loads of 101 intensities. Results show that the aerodynamic load is nonlinearly coupled with seismic load at rated wind speed, and their coupling effect should be adequately considered during the assessment of seismic response. At a constant wind speed, the maximum bending moment of tower base remains unchanged at first, and increases linearly then. In the case of low-intensity earthquakes, the maximum bending moment at different elevations is linearly related to the height of tower; with the rise of seismic intensity, the relationship between bending moment and tower height turns to be nonlinear, and the tower top moment reaches the maximum at rated wind speed.
wind turbine; seismic load; dynamic response; structural strength of tower
2016-06-22
2016-12-06
国家自然科学基金资助项目(51176129,51676131);上海市科委资助项目(13DZ2260900)
杨 阳(1992-),男,江西宜春人,博士研究生,主要从事风力机复杂工况气动弹性响应方面的研究.
李 春(通信作者),男,教授,博士,电话(Tel.):13301777337;E-mail:lichun-usst@163.com.
1674-7607(2017)11-0938-07
TK83
A
480.6040

