单元机组协调控制系统综合性能评价
袁桂丽, 陆斯悦, 房 方
(华北电力大学 控制与计算机工程学院,北京 102206)
单元机组协调控制系统综合性能评价
袁桂丽, 陆斯悦, 房 方
(华北电力大学 控制与计算机工程学院,北京 102206)
针对多变量形式的单元机组协调控制系统,提出一种基于等效开环传递函数的性能评价方法.将该方法与最小信息熵指标相结合,解决了协调控制系统受到非高斯噪声干扰时,传统多变量评价方法对系统随机性性能评价不准确的问题.将系统确定性性能指标处理成标量形式,通过子目标乘除法与随机性性能指标结合,得到兼顾确定性性能与随机性性能的综合性能指标.利用该综合性能指标指导协调控制系统控制器设计,将其作为目标函数,通过优化算法对控制器参数进行寻优,得到最优控制性能.以最优指标作为基准,对系统在运行期间的性能进行监测与评价.结果表明:对于该协调控制系统,自抗扰控制器比内模PI控制器具有更好的综合性能,稳健性也更好.
协调控制系统; 等效开环传递函数; 最小信息熵; 自抗扰控制; 性能评价
随着电力生产过程逐步大型化和复杂化,能否对机组实现良好的控制关乎到安全、环保、效益等诸多方面[1].单元机组协调控制系统是火电厂最重要的控制系统之一,在锅炉-汽轮机控制中起主导作用,因此应及时对该系统进行性能评价与监测,以保证机组运行的安全与效率.然而,协调控制系统是一个多输入多输出系统,回路间存在复杂的耦合.此外,在实际运行中系统也会受到大量噪声干扰,这些噪声的分布往往是非高斯型的,且难以预测,这给评价工作带来了一定困难.目前,针对单元机组协调控制系统性能评价的研究成果较少[2],因此研究其相关理论和方法对实现非高斯扰动下多变量形式的协调系统性能评价非常重要.
控制系统性能评价最常用的方法是最小方差性能评价方法,Huang等[3]将其扩展到多变量系统中,之后又有一些学者对该方法进行了改进.Xia等[4]提出用输入-输出的时间延迟来估计多变量系统的最小方差上下界;Yu等[5]研究了协方差基准;Zhao等[6]将广义最小方差基准推广到多变量系统中.近年来,对于多变量系统的性能评价方法已不再局限于最小方差基准.如蔡宏斌等[7]提出了基于主元分析和最小二乘支持向量机相结合的多变量性能评价方法;杨全振等[8]提出了基于主元回归方法的多变量控制系统性能评价方法;Khamseh等[9]提出了基于传感器融合技术的多变量性能评价方法等.
上述传统性能评价方法大多基于平稳的高斯噪声扰动.对于非高斯扰动下的系统,有学者提出通过计算跟踪误差熵的形式来反映其随机性能.常用的熵描述形式有Shannon熵[10]、有理熵[11]和二阶renyi熵[12]等.但这几种熵指标大多是针对单回路系统的,尚未扩展到多变量系统的性能评价中.
此外,上述指标只涉及到系统的随机性性能,而在实际火电机组运行过程中,确定性性能同样受到关注,如调节时间、超调量、时间乘以误差绝对值积分(ITAE)等.为了同时说明确定性与随机性这两方面的性能,需要寻找一个能够同时评价控制器各方面性能,获得更为全面、有效评价结果的综合性能指标,这样既通过该指标对系统控制器的设计进行指导,也可以对系统的运行情况进行监视.
笔者针对单元机组协调控制系统的多变量非高斯分布特性,提出了一种基于等效开环传递函数的评价方法.基于“等效开环过程”[13],将多变量系统等效为若干个包含其他回路之间耦合作用动态信息特征的单回路,引入最小信息熵指标,从而完成非高斯噪声下多变量控制系统的性能评价.同时提出了一种根据子目标乘除法计算的综合性能指标,直接全面地反映单元机组协调控制系统的整体性能.最后,对某300 MW燃煤直流炉再热机组协调控制系统进行了仿真.采用内模PI和自抗扰2种控制策略,以综合性能指标作为目标函数对控制器参数进行寻优,得到了最优控制器参数和最优性能指标,并对2种控制器下运行过程的性能进行了监控.
1 基于等效开环传递函数的单元机组协调控制系统性能评价
1.1多变量系统的等效开环传递函数

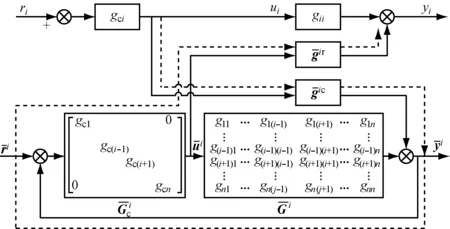
图1 多变量控制系统等效开环传递函数原理图
Fig.1 Schematic diagram of the equivalent open-loop transfer function for multivariable control systems
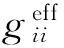
等效开环传递函数的推导过程如下:

(1)
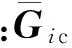
yi与ui的关系式为:
(2)
式中:I为单位矩阵.
由式(2)可知,耦合存在于不同回路的控制器中,所以对单回路的控制和评价方法不能直接应用到多变量系统中.
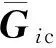
(3)
第i回路的等效开环传递函数为:
(4)
在进一步推导等效开环传递函数公式前引入相对增益矩阵的定义.Λ为传递函数矩阵G(s)的相对增益矩阵(RGA),其表达式如下:
(5)
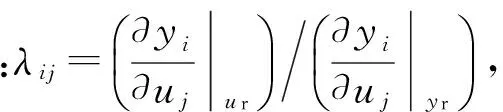
RGA是根据稳态增益计算得到的,因而实际中直接采用式(6)进行计算:
Λ=G(0)⊗(G(0)-1)T
(6)
式(5)中的相对增益矩阵是在获得稳态增益后计算得到的,即不包括动态信息,因此在描述和分析系统耦合时存在较多不足.因此人们提出了动态相对增益矩阵(DRGA),其是利用对象的传递函数来代替稳态增益,即Λii={G(s)⊗[G(s)-1]T}ii,将其代入式(4)可得EOTF方程:
(7)
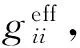
因此,图1所示的分散控制结构可完全转化为图2所示的结构.
单元机组协调控制系统可用燃烧率μB和汽轮机调汽阀门开度μT这2个输入变量,以及主汽压力pT和机组实发功率NE这2个输出量来描述.等效传递函数方框图见图3,其中Cn代替第n回路控制器.
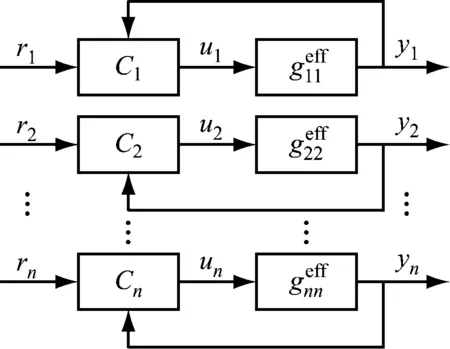
图2 简化后的等效单回路系统Fig.2 Equivalent single loop system after simplification
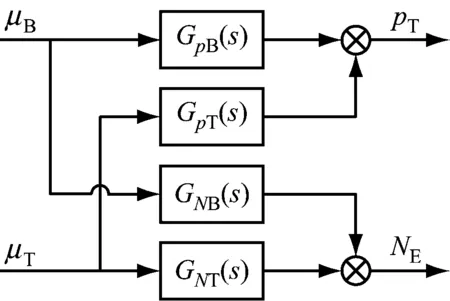
图3 单元机组协调控制系统传递函数方框图
Fig.3 Transfer function block diagram for the coordinated control system of thermal power unit
图3中,GpB(s)为机前压力pT对燃烧指令μB的传递函数,GpT(s)为机前压力pT对调汽阀开度指令μT的传递函数,GNB(s)为实发功率NE对燃烧指令μB的传递函数,GNT(s)为实发功率NE对汽轮机调汽阀门开度μT的传递函数.
根据DRGA的概念,计算2个回路的动态相对增益:
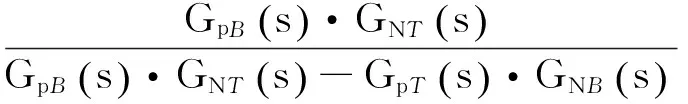
(8)
将式(8)代入式(7)后,可以得到两入两出单元机组协调控制系统的等效开环传递函数:
(9)
(10)
由于等效后的单回路已包含原回路之间的耦合信息,所以对多变量系统的性能评价可转化为对各个单回路的性能评价.将所有单回路性能指标相加,即可得到多变量系统的性能指标.为了便于比较,也可以将各单回路性能指标的平均值作为多变量系统的性能指标.
对于n入n出系统:
(11)
式中:η为多变量系统的性能指标;ηi为第i个单回路的性能指标.
对于协调控制系统:
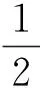
(12)
1.2控制系统性能评价基准
1.2.1 随机性性能指标
在随机性性能评价中,最小方差指标的应用最普遍,该指标可以很好地解决线性高斯系统的性能评价问题.但Zhang等[12]指出若将最小方差指标应用到非高斯分布扰动的控制过程中,则得到的性能评价结果是不合理的.
同时,在实际的操作过程中,系统干扰噪声的分布往往是难以预测的.对于非线性非高斯系统,笔者以信息熵为基准来衡量其性能,信息熵能够刻画系统随机变量的不确定度.
通常情况下,信息熵指的是Shannon熵.对于随机变量x,其连续的信息熵H定义如下:
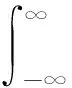
(13)
式中:γ(x)为变量x的概率密度函数,可通过直方图法或核密度估计法求得.
性能评价中最重要的工作之一就是寻找性能基准.Meng等[10]通过计算最小信息熵控制下系统的跟踪误差信息熵,得出了最小信息熵基准,即MIE基准:
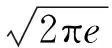
(14)
式中:e为欧拉常数;δ为扰动的方差.
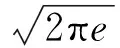
为了简化运算,并保证指标值的单调递增性,去除负熵值的影响,取指数函数映射f(x)=e(x),则基于最小信息熵的性能评价指标ηmie定义为:
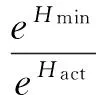
(15)
式中:Hact为回路跟踪误差的实际信息熵.
在最小信息熵基准的衡量下,该指标最小值趋于0.指标越接近于1,跟踪误差的信息熵越小,性能越好.
结合式(11),可得到n入n出系统基于等效开环传递函数的多变量系统随机性能指标:
(16)
式中:ηsto-i为第i个回路的随机性性能指标,可由式(15)计算得到,也可由最小方差指标等其他性能基准计算得到.
对于协调控制系统,等效开环传递函数的多变量系统随机性性能指标为:
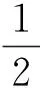
(17)
1.2.2 确定性性能指标
在经典控制理论中,确定性性能代表了对控制性能的基本要求,能够衡量系统对设定值的跟踪能力以及对负载扰动的抑制能力.常见的确定性性能指标主要有2种.一种是系统阶跃响应指标,如超调量、上升时间和调节时间等.这种单项性能指标只能反映系统某一方面的确定性性能.然而系统中这些量往往是互相联系并有所牵制的,若想了解系统整体的确定性性能,可选用另一种确定性性能指标,即误差积分型指标.
笔者选取式(18)所示的时间加权绝对误差积分(ITAE)指标.这一指标在计算上具有一定的简便性,而且能够较好地反映控制系统的准确性与快速性,在描述性能方面十分优秀.
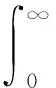
(18)
式中:t为过程调节时间.
为了得到统一的性能基准,并简化计算过程,对该指标进行无量纲化处理,使其可以同时对不同系统采用相同的基准进行评价.处理方法如下:
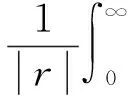
(19)
式中:r为系统输入的阶跃值;ts为标量的调节时间,ts=t/τ,其中τ为过程延迟.
将式(19)代入式(18)后可得:
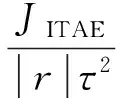
(20)
对于n入n出系统,可依次对各输入施加阶跃扰动,其他输入为零输入,计算各个输出的JITAE′,然后将所有结果相加,就可以得到整个多变量系统的确定性性能指标.具体表达式如下:
(21)
式中:JITAE′-ij为第i个输入施加阶跃扰动且其他输入为零输入时,第j个输出的标量ITAE值.
对于协调控制系统,确定性性能指标为:
Jdete=JITAE′-11+JITAE′-12+JITAE′-21+JITAE′-22
(22)
2 单元机组协调控制系统性能综合评价
控制系统综合性能评价是一个多目标优化问题中的统一目标函数问题.将各个子目标处理为标量形式,可选用子目标乘除法来对综合指标进行计算.结合工业过程的实际情况,选用式(23)所示的多变量系统的综合性能计算式:
J=Jdete×(1-Jsto-g)×(1-Jsto-ng)
(23)
式中:Jdete为系统确定性性能指标;Jsto-g为系统在高斯扰动下的随机性性能指标;Jsto-ng为系统在非高斯扰动下的随机性性能指标.
将式(22)作为确定性性能指标的求取方法,将式(17)作为高斯扰动和非高斯扰动下随机性性能指标的求取方法,即可得到单元机组协调控制系统的综合性能指标.整个指标的数值越小,系统的综合性能越好.
3 单元机组机炉协调控制系统性能评价仿真
单元机组是一类典型的多入多出系统,且具有回路间耦合较强、模型参数不确定、延迟较大、干扰难以预测等特点,是工业中的典型系统,也是现代电厂自动化系统中最核心的部分.因此,单元机组协调
控制系统具有很高的理论和实际研究价值.
3.1问题描述
以国产300 MW燃煤直流炉再热机组作为被控对象[14],将单元机组协调控制系统等价为2个单回路系统.其在100%负荷工况下的近似线性传递函数模型如下:
(24)
采用文献[14]给出的配对方式进行配对:
(25)
配对后的模型为:
(26)
根据式(9)~式(10)求取等效开环传递函数,并简化成一阶惯性加纯迟延模型:
(27)
(28)
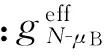
3.2仿真研究
3.2.1 高斯扰动下机炉协调控制系统性能评价仿真
选取文献[15]中二阶线性自抗扰控制器(ADRC)对机炉协调控制系统进行控制.主要参数有扩张状态观测器(ESO)带宽ωo、控制器带宽ωc和控制器参数b0.
令等效的2个单回路模型与原模型均处于表1中初始参数的控制器下,皆施加均值为0、方差为0.8的高斯白噪声扰动,分别得到机组的实发功率和主汽压力输出.应用文献[16]中的多变量最小方差基准对原模型进行评价,得到多变量最小方差指标. 等效模型采用式(17)进行评价,式中的ηsto-i分别应用文献[16]中的最小方差评价基准和式(14)最小信息熵基准.3种评价方法得到的结果见图4,其中纵坐标为性能指标,横坐标为扩张观测器带宽ωo的增量Δωo.

表1 初始自抗扰控制器参数
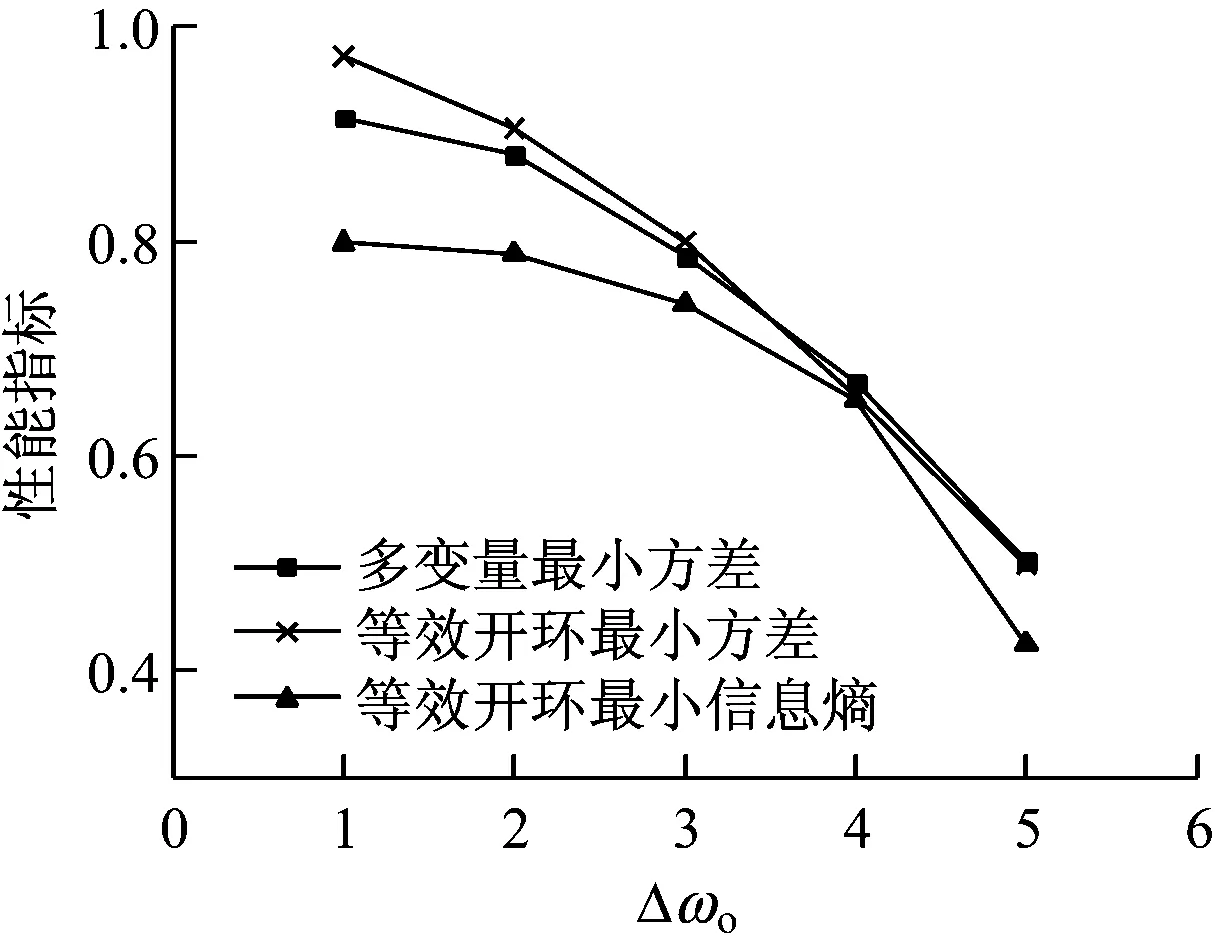
图4 3种评价方法结果对比Fig.4 Comparison among three performance assessment results
从图4可以看出,随着Δωo增大,2种最小方差评价结果基本相同.由此可以证明等效开环传递函数多变量性能评价方法较为准确,具有可行性.对于等效开环最小信息熵指标,由于基准不同,得到的结果与多变量最小方差指标有一些差别,但其所反映的性能变化趋势仍与其他2种方法一致,即最小信息熵指标可以用来评价系统在高斯扰动下的随机性性能.
3.2.2 非高斯扰动下机炉协调控制系统性能评价仿真
由文献[12]可知,用最小方差指标处理的动态系统噪声需遵循高斯分布,而若选用最小信息熵指标,则噪声不受分布的限制.对协调系统的2个回路施加服从(1,1.5)韦布尔分布的非高斯噪声.令ADRC控制器的观测器带宽ωo在0.2~5内选取20组参数,得到了系统非高斯扰动下跟踪误差概率密度函数(见图5).由图5可以看出,曲线从上到下依次对应的参数ωo逐渐增大.
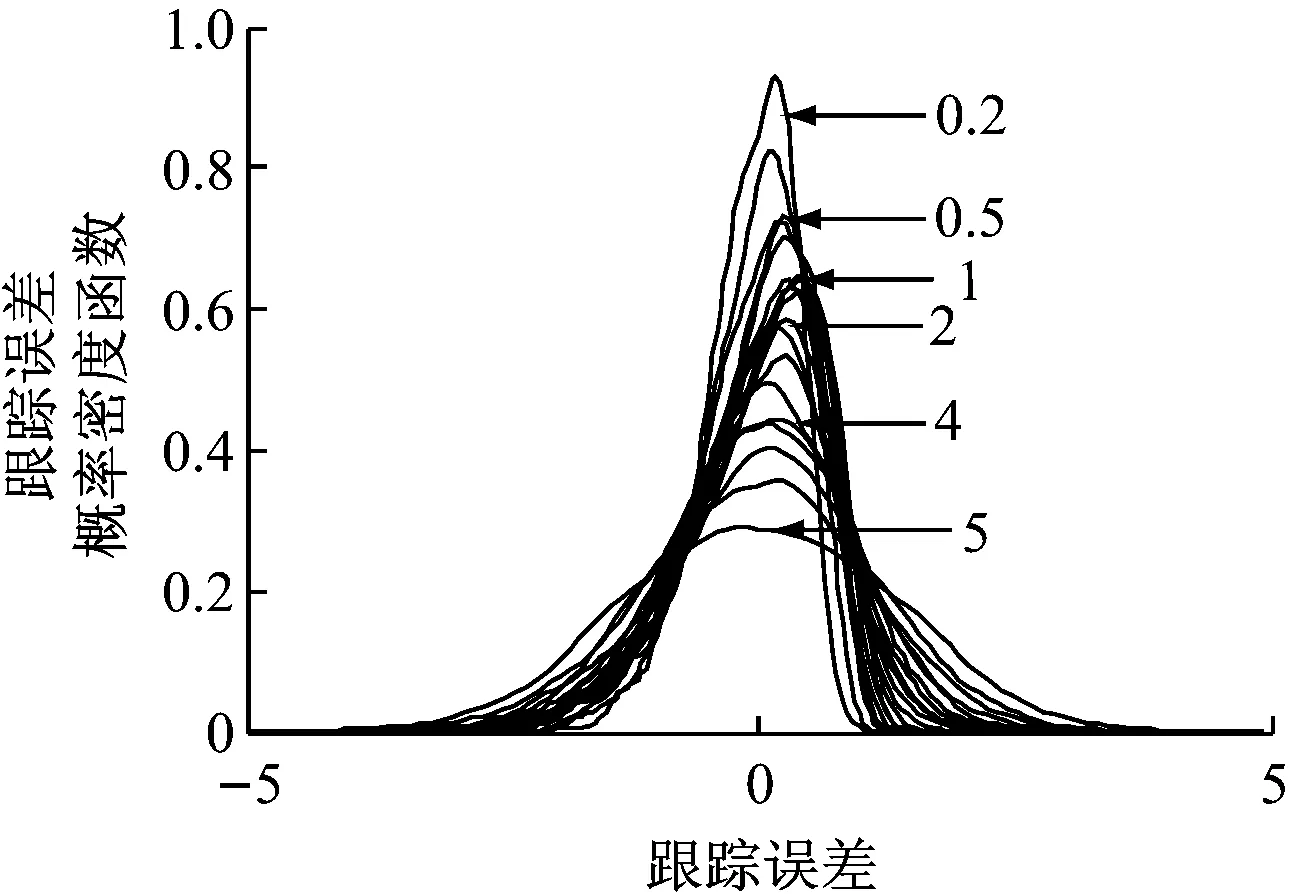
图5 非高斯扰动下主汽压力跟踪误差概率密度函数
Fig.5 Probability density function of tracking error of main steam pressure under non-Gaussian disturbance
一般情况下,ωo越大,ESO反应速度越快,观测能力越强,但ESO对噪声的敏感性也随之增大,即系统的随机性性能下降.从图5可以看出,从下至上曲线形状变得更尖,更窄,即随着ωo的减小,系统抵抗随机外扰的能力逐渐增强,随机性性能逐渐改善.
分别用最小方差和最小信息熵2种基准对系统性能进行评价,结果见图6.从图6可以看出,当扰动为非高斯分布时,最小信息熵基准的评价结果与概率密度函数曲线所表现出的性能一致,即随着ωo的减小而逐渐变好;而最小方差基准的评价结果则随着ωo的减小而先上升再下降,与实际情况相矛盾.这一结果充分说明,在非高斯扰动下进行随机性性能评价时不能选用最小方差指标,而应选用最小信息熵指标.

图6 非高斯扰动下最小方差与最小信息熵基准评价结果对比
Fig.6 Comparison of evaluation results between the minimum variance and the minimum information entropy index under non-Gaussian disturbance
综上可知,系统扰动分布在高斯型或非高斯型情况下,均能用最小信息熵指标对系统性能进行有效的评价;并且该方法不需估计系统延迟,计算量小,处理时间短,因此笔者选用最小信息熵基准作为综合性能指标中随机性性能的评价基准.
3.2.3 机炉协调控制系统综合性能评价仿真
多变量控制系统的结构复杂,控制器的设计和参数整定具有一定难度.例如ADRC,除扩张观测器带宽ωo需根据性能调整外,参数ωc和b0也需要根据具体控制要求来进行调整.通常,ωc越大,b0越小,控制器的控制作用越强,系统响应越快,但超调和震荡会变大.所以,将这3个参数整定至最优是有一定难度的.
选用式(23)所示的综合性能指标作为目标函数对ADRC参数进行寻优,即可找到兼顾确定性性能和随机性性能的最优控制器参数.其中,确定性性能用式(22)来评价,评价时系统所施加的扰动为单位阶跃扰动;高斯和非高斯扰动下随机性性能皆用式(17)进行评价,式中ηsto-i选取最小信息熵为基准.评价时对系统施加均值为0、方差为0.8的高斯白噪声扰动和服从(1,1.5)韦布尔分布的非高斯噪声扰动.
采用线性递减权重粒子群优化算法,种群规模N=50,学习因子c1=2.3,c2=1.7,惯性权重的最大值ωmax=0.9,最小值ωmin=0.4,迭代次数M=50.寻优得到的最优参数见表2.得到该控制器参数下系统最优综合性能指标JADRC=39.375.
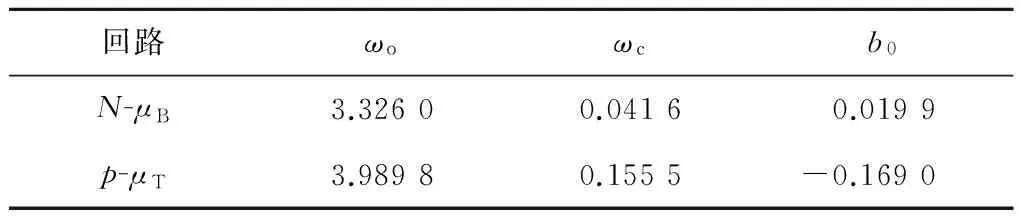
表2 自抗扰控制器最优参数
为了比较不同控制策略的控制效果,选用文献[17]中提出的内模PI(IMC-PI)控制器对协调控制系统进行控制.同样将式(23)作为目标函数,通过标准粒子群优化算法对IMC-PI控制器参数进行寻优,其中种群规模N=20,学习因子c1=2,c2=2,惯性权重ω=0.5,迭代次数M=50.寻优得到的最优控制器参数为:
N-μB回路:Kp1=7.37,Ti1=227.123
p-μT回路:Kp2=-5.03,Ti2=71.587
式中:Kp为比例系数;Ti为积分时间常数.此时系统的最优综合性能指标JIMC-PI=46.611.
对比JADRC与JIMC-PI可以看出,在整定至最优参数的情况下,ADRC控制能达到更好的性能,即对于该协调控制系统选用ADRC控制策略的控制效果更好.
图7和图8给出了系统在2种控制器下的输出阶跃响应曲线,以及以主汽压力回路为例的高斯和非高斯噪声下跟踪误差概率密度函数曲线.
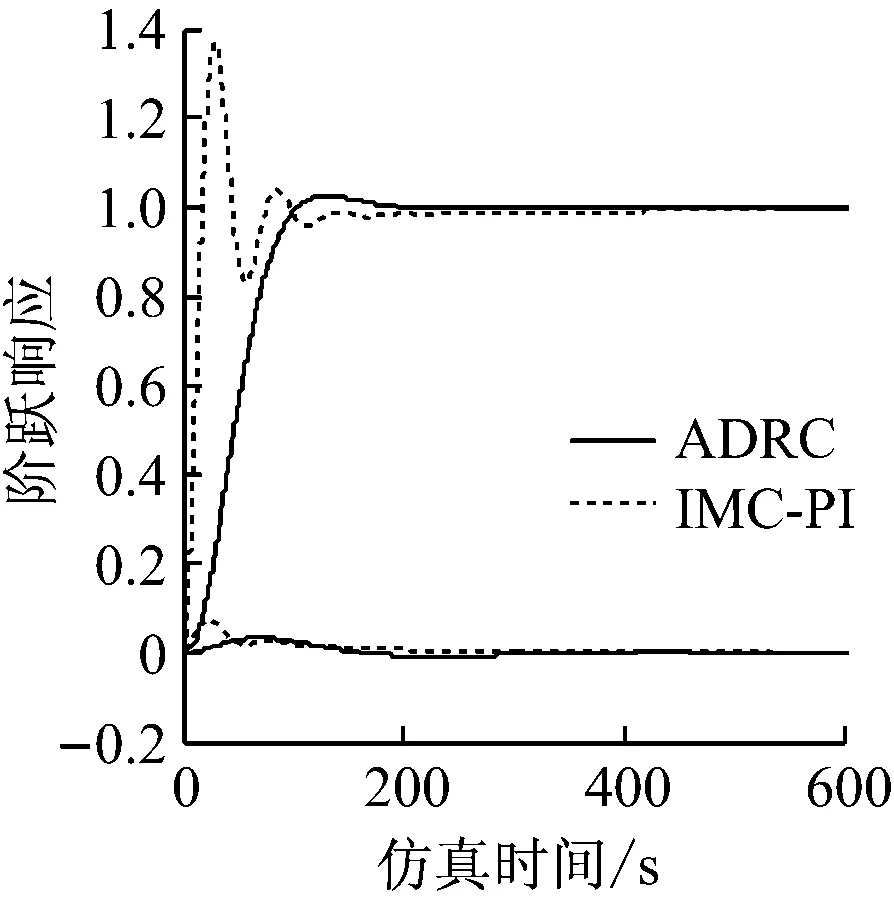
(a) 功率设定值阶跃响应曲线
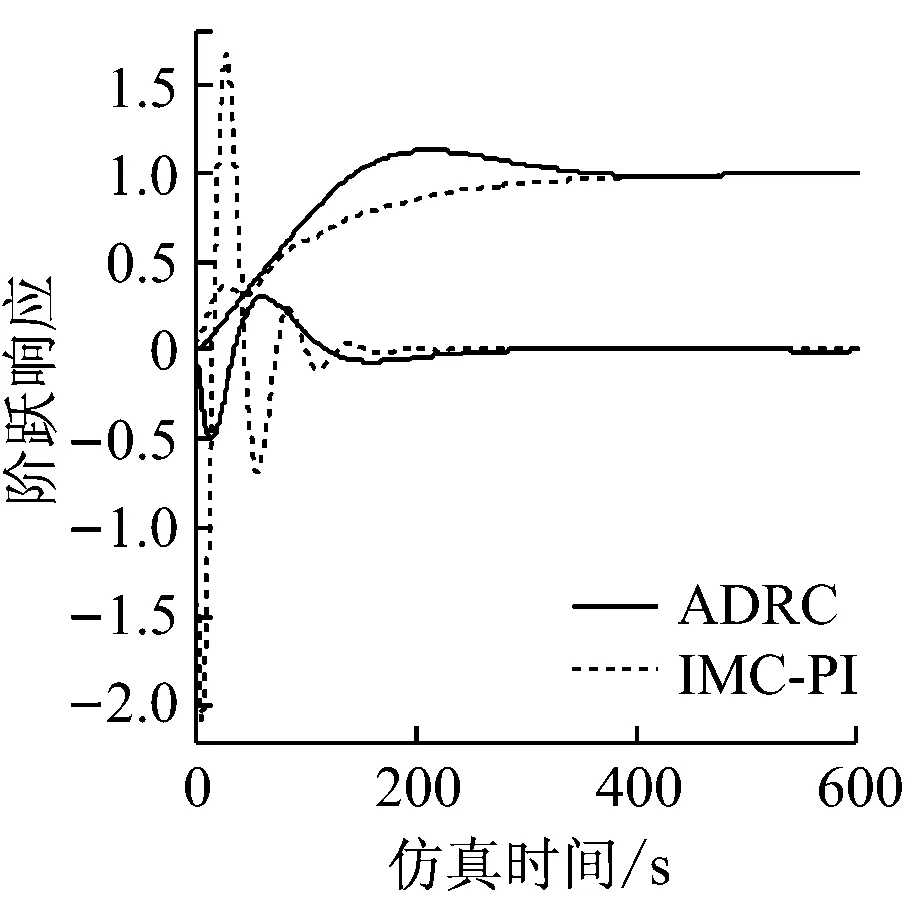
(b) 主汽压力设定值阶跃响应曲线图7 2种控制策略下功率设定值和主汽压力设定值的阶跃响应曲线
Fig.7 Step response curves of power setpoint and main steam pressure setpoint under two control strategies
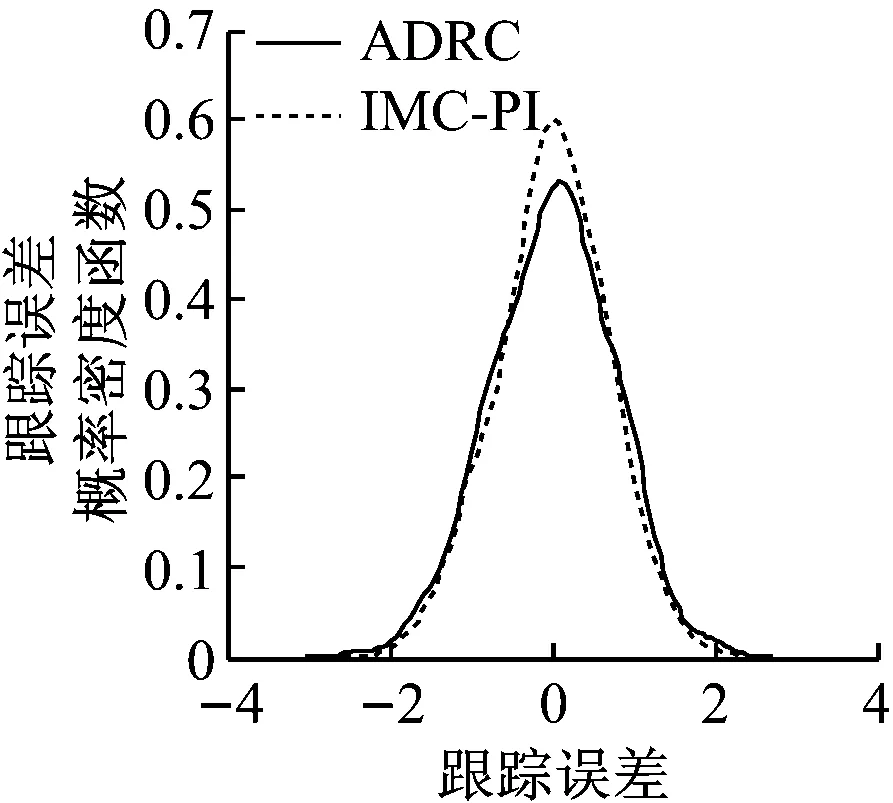
(a) 高斯扰动下
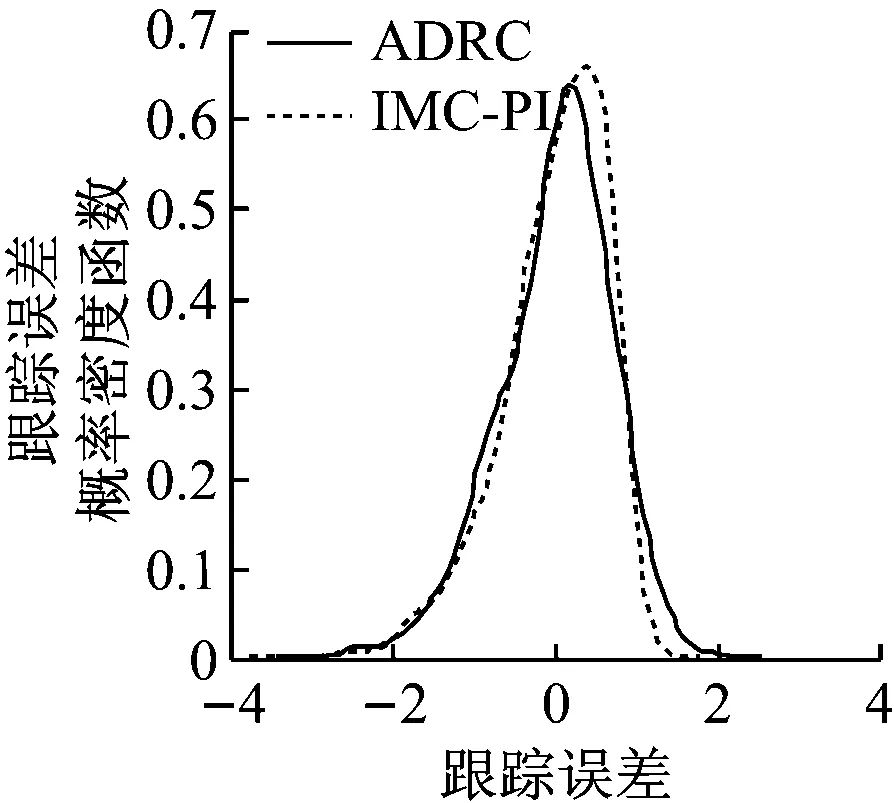
(b) 非高斯扰动下
图8 2种控制策略在高斯扰动和非高斯扰动下的主汽压力跟踪误差概率密度函数
Fig.8 Probability density function of tracking error of main steam pressure for two control strategies under Gaussian and non-Gaussian disturbances
从图7可以看出,采用ADRC对协调系统进行控制能够有效减少回路之间的耦合,调节时间相近,但超调量较小,整体的确定性性能有所提高.从图8可以看出,2种控制策略在高斯扰动和非高斯扰动下的随机性能较为接近,但IMC-PI控制稍胜一筹.通过综合指标可以定量计算出ADRC控制的综合性能更加优越.
对于已经设计好的控制系统,在运行一段时间后,由于受到各种因素的影响,其良好的性能会有所下降.将寻优得到的综合性能指标作为基准,即可对系统性能进行监测与评估.
假设在运行过程中系统产生了过程特性变化或执行机构磨损等问题,知识模型产生了摄动.令式(24)中所有参数减小(增大)15%,计算当前系统的综合性能指标,最后以最优性能为基准计算性能下降的比例,结果见表3.
由表3可知,在模型参数摄动的情况下,自抗扰控制器的稳健性更好.说明若选用自抗扰控制器对该系统进行控制,运行一段时间后其性能仍能满足要求;若选用内模PI控制器进行控制,则性能下降得较多,运行人员应对控制回路的运行状态进行检查与分析.
表3模型参数摄动时的系统性能指标
Tab.3Systemperformanceindexesduringperturbationofmodelparameters
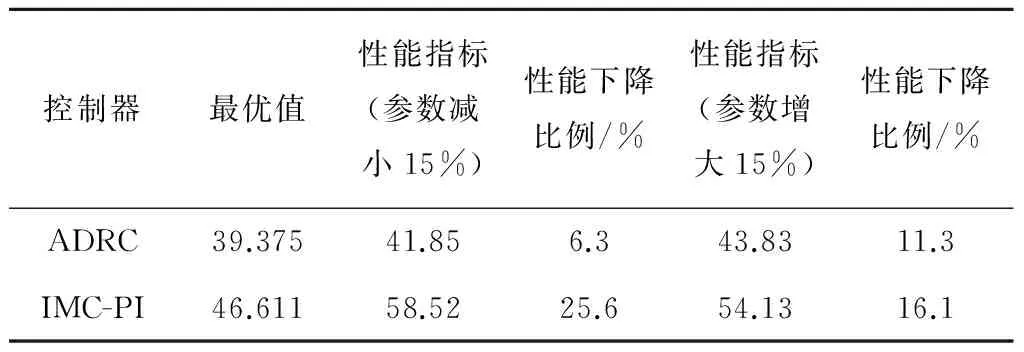
控制器最优值性能指标(参数减小15%)性能下降比例/%性能指标(参数增大15%)性能下降比例/%ADRC39.37541.856.343.8311.3IMC-PI46.61158.5225.654.1316.1
若要将所提出的单元机组协调控制系统应用到实际中,可选取系统在负荷指令发生变化时段的历史运行数据进行评价.由于实际历史运行数据既反映了系统输出对设定值的跟踪情况,又反映了系统对随机噪声干扰的抑制情况,因此可以直接通过一段时间内的运行数据来计算控制系统的综合性能.在进行评价前,需对数据进行预处理.如可采用趋势项提取的方式,分离出数据的扰动项与趋势项,通过扰动项数据可计算系统当前的随机性性能指标,通过趋势项数据可计算系统当前的确定性性能指标.
4 结 论
(1)根据协调控制系统具有非高斯多变量的特性,提出了基于等效开环传递函数的多变量控制系统性能评价方法,引入可计算系统在非高斯扰动下性能的最小信息熵性能指标解决这一问题.
(2)提出了一种根据子目标乘除法计算的综合性能指标,这一指标能够综合反映系统确定性性能和随机性性能.
(3)采用自抗扰控制和内模PI控制2种控制策略对某300 MW燃煤直流炉再热机组协调控制系统进行控制,以综合性能指标为目标函数对2种控制器参数进行寻优,得到了权衡系统确定性和随机性的最优参数以及性能指标,对比得出自抗扰控制器的综合性能更强.以寻优得到的最优性能指标为基准,实现对系统在运行过程中的性能进行监测,指导运行人员对系统进行操作.
[1] 孟庆伟, 房方, 刘吉臻. 一种热工控制系统综合性能的评价方法[J].中国电机工程学报, 2011, 31(23): 101-107.
MENG Qingwei, FANG Fang, LIU Jizhen. An assessment method for comprehensive performance of thermal control system[J].ProceedingsoftheCSEE, 2011, 31(23): 101-107.
[2] 田靖雨, 王印松, 李士哲, 等. 基于协方差指标的火电机组协调控制系统性能模糊评价方法[J].热力发电, 2016, 45(2): 47-51.
TIAN Jingyu, WANG Yinsong, LI Shizhe, et al. Fuzzy assessment of performance of coordinated control system in thermal power unit based on covariance index[J].ThermalPowerGeneration, 2016, 45(2): 47-51.
[3] HUANG B, SHAH S L. Practical issues in multivariable feedback control performance assessment[J].JournalofProcessControl, 1998, 8(5/6): 421-430.
[4] XIA H, MAJECKI P, ORDYS A, et al. Performance assessment of MIMO systems based on I/O delay information[J].JournalofProcessControl, 2006, 16(4): 373-383.
[5] YU J, QIN S J. Statistical MIMO controller performance monitoring. Part I: data-driven covariance benchmark[J].JournalofProcessControl, 2008, 18(3/4): 277-296.
[6] ZHAO Y, SU H Y, CHU J,et al. Multivariable control performance assessment based on generalized minimum variance benchmark[C]//Proceedingsofthe48thIEEEConferenceonDecisionandControl,2009HeldJointlywiththe200928thChineseControlConference.Shanghai, China: IEEE, 2009: 1902-1907.
[7] 蔡宏斌, 苏成利. PCA-LSSVM方法的控制系统性能评估[J].自动化仪表, 2014, 35(1): 10-14.
CAI Hongbin, SU Chengli.Performance assessment based on PCA-LSSVM for control system[J].ProcessAutomationInstrumentation, 2014, 35(1): 10-14.
[8] 杨全振,苏成利. 基于主元回归方法的多变量控制系统性能评估[J].化工自动化及仪表, 2013, 40(1): 8-11.
YANG Quanzhen,SU Chengli. Mutivariable control system performance assessment based on principal component regression method[J].ControlandInstrumentsinChemicalIndustry, 2013, 40(1): 8-11.
[9] KHAMSEH S A, SEDIGH A K, MOSHIRI B, et al. Control performance assessment based on sensor fusion techniques[J].ControlEngineeringPractice, 2016, 49: 14-28.
[10] MENG Q W, FANG F, LIU J Z. Minimum-information-entropy-based control performance assessment[J].Entropy, 2013, 15(3): 943-959.
[11] ZHOU J L, WANG X, ZHANG J F,et al. A new measure of uncertainty and the control loop performance assessment for output stochastic distribution systems[J].IEEETransactionsonAutomaticControl, 2014, 60(9): 2524-2529.
[12] ZHANG Jianhua, JIANG Man, CHEN Junghui.Minimum entropy-based performance assessment of feedback control loops subjected to non-gaussiandisturbances[J].JournalofProcessControl, 2014, 24(11): 1660-1670.
[13] VU T N L, LEE M. Independent design of multi-loop PI/PID controllers for interacting multivariable processes[J].JournalofProcessControl, 2010, 20(8): 922-933.
[14] 刘翔, 姜学智, 李东海, 等. 火电单元机组机炉协调自抗扰的控制[J].控制理论与应用, 2001, 18(增刊1): 149-152.
LIU Xiang, JIANG Xuezhi,LI Donghai,et al.Coordinated auto-disturbance-rejection control for boiler-turbine unit[J].ControlTheoryamp;Applications, 2001, 18(S1): 149-152.
[15] 马永光, 李超, 马良玉, 等. 1 000 MW超超临界机组协调系统的线性自抗扰控制[J].动力工程学报, 2014, 34(8): 618-623.
MA Yongguang, LI Chao, MA Liangyu, et al. Linear active disturbance rejection control on coordinated system of a 1 000 MW ultra-supercritical power unit[J].JournalofChineseSocietyofPowerEngineering, 2014, 34(8): 618-623.
[16] 杜娟. 控制系统性能评价及优化[D]. 北京: 华北电力大学, 2015.
[17] 孟庆伟, 刘吉臻, 王瑞琪, 等. 基于电网“两个细则”的PI控制器优化整定[J].电机与控制学报, 2013, 17(10): 91-96, 108.
MENG Qingwei, LIU Jizhen, WANG Ruiqi,et al."Two Documents" issued by the grid based optimal tuning of PI controller[J].ElectricMachinesandControl, 2013, 17(10): 91-96, 108.
ComprehensivePerformanceAssessmentonCoordinatedControlSystemofThermalPowerUnits
YUANGuili,LUSiyue,FANGFang
(School of Control and Computer Engineering, North China Electric Power University, Beijing 102206, China)
A performance evaluation method based on equivalent open-loop transfer function was proposed for the multi-variable coordination control system of thermal power units. Combined with the minimum information entropy index, this method is able to solve the problem that traditional multivariable performance assessment method cannot accurately evaluate the stochastic performance of the coordinated control system when the system is disturbed by non-Gaussian noise. By transforming the deterministic index of system into the scalar form, and by combining the sub goal multiplication and division with the stochastic performance, a comprehensive index of both deterministic performance and stochastic performance is then obtained, which can be used to guide the design of the coordinated controller. Taking the comprehensive index as the objective function, an optimal control performance could be acquired through optimization of the controller parameters. The performance of the coordinated control system in the thermal power unit was monitored and evaluated in the process of operation by using the optimal index as a benchmark. Simulation results show that for the coordinated control system, the comprehensive performance and robustness of the active disturbance rejection controller is better than those of internal model PI controllers.
coordinated control system; equivalent open-loop transfer function; minimum information entropy; active disturbance rejection control; performance evaluation
2016-10-27
2016-12-20
国家自然科学基金资助项目(61240037,51676068)
袁桂丽(1971-),女,内蒙古赤峰人,教授,博士,研究方向为先进控制策略及其应用、电力系统控制与优化调度.
电话(Tel.):13521330721;E-mail:guili_yuan@163.com.
1674-7607(2017)11-0895-08
TP202
A
470.20

