汽车悬架非线性螺旋弹簧的设计与仿真分析

李军， 李学鋆

(重庆交通大学 机电与车辆工程学院， 重庆 400074)

汽车悬架非线性螺旋弹簧的设计与仿真分析

李军， 李学鋆

(重庆交通大学 机电与车辆工程学院， 重庆 400074)

通过拟合空气弹簧的特性曲线，并利用螺旋弹簧刚度计算公式得到螺旋弹簧中径和高度的关系，在ANSYS对非线性螺旋弹簧模型进行载荷分析，并对结果数据进行拟合，得到所设计弹簧的特性曲线方程.对建立四分之一悬架系统模型的动力学方程，利用摄动法将非线性弹簧特性曲线方程线性化处理且带入动力学方程中，在MATLAB/Simulink中进行仿真分析,以及与四分之一定刚度悬架系统对比分析.仿真结果表明:利用空气弹簧非线性特性所设计的非线性弹簧可有效提高车辆的舒适性和平顺性，相对于定刚度悬架其各参数指标均有很大程度的改善和提升.

汽车； 空气弹簧； 非线性螺旋弹簧； 悬架系统； 曲线拟合

弹性元件作为悬架系统的基础元件，直接影响车辆行驶的平顺性,合理设计弹性元件对于减少外力对车辆的影响，改善汽车的平顺性有很大的作用[1].文献[2]利用多目标寻优寻找悬架螺旋弹簧的三点非线性刚度特性曲线，从而使得被动悬架刚度特性由原来的弱非线性向强非线性转变，大大改善了车辆安全舒适性.文献[3]以弹簧离合器为对象对弹簧的结构参数进行分析建模，并采用有限元方法对弹簧离合器在传递过程的应力和弹簧的径向、轴向、扭转刚度特性进行分析.除此之外,还利用多目标优化算法对所建立的弹簧的目标函数和约束条件进行优化计算，从而得到有限组解，对已有的弹簧进行改进优化.但该方法在优化赋权重时主观性较强，且是对已有非线性弹簧进行的优化计算.非线性螺旋弹簧具有很好的非线性性能，可以提高车辆悬架系统的平顺性,但其设计难度大，设计时往往依靠经验设计.本文通过拟合得到空气弹簧的非线性特性曲线，并利用离散法将空气弹簧的非线性特性结合到非线性螺旋弹簧的设计上；最后，在MATLAB/Simulink上搭建四分之一悬架系统仿真模型，并与四分之一的定刚度悬架进行对比分析.

1 空气弹簧特性曲线的拟合

理想气体的状态方程是计算空气弹簧动态特性的基础[4-5]，有

式(1)中:p1，p2为状态1，2时的气体压力；V1，V2为状态1,2时的气体体积；λ为空气多变指数，空气弹簧一般取1.3～1.4.

在考虑大气压强情况下，空气弹簧的承载力计算式为

式(2)中:pi为空气弹簧表面压力，pi=p-pa；Ae为空气弹簧有效面积.对弹簧位移x求导,可得到空气弹簧的刚度K为

根据文献[6]空气弹簧有效面积与变形量成线性关系，有

式中:Ae0为空气弹簧初始有效面积；k为有效面积余位移线性比例系数；Δx为空气弹簧的变形量.

联立式(3)，(4),可得

图1 位移-力关系的特性曲线Fig.1 Displacement-force diagram

将空气弹簧的物理参数带入式(5)，可绘制出力-位移(F-Δ)的关系特性曲线，如图1所示.假定所设计的螺旋弹簧刚度特性满足式(5)，且螺旋弹簧轴向的刚度是连续的.弹簧中径D与刚度K的关系为

将上式代入式(5)，可以得出位移-中径(Δ-D)的关系函数.

空气弹簧的物理参数和建模参数,如表1，2所示.表1,2中：Ae为有效面积；dAe/dx为有效面积变化率；L为空气弹簧本体体积；h为标准工作高度；p0为初始工作内压；ntot为总圈数；n为有效圈数；d为簧丝直径；t为螺距；H0为自由高度；E为弹性模量；γ为泊松比.

根据表1,2中的参数绘制出位移-中径关系曲线，如图2所示.由图2可知:每一个位移值对应一个中径值，表明了每一个位移相当于对应中径当量的圆柱螺旋弹簧.即每个当量中径值的螺旋弹簧皆对应唯一一个位移值，所有的位移值连续起来就组成了连续的中径可变的圆柱螺旋弹簧.

表1 空气弹簧的物理参数表Tab.1 Physical parameters of air spring

表2 空气弹簧的建模参数Tab.2 Spring modeling parameters

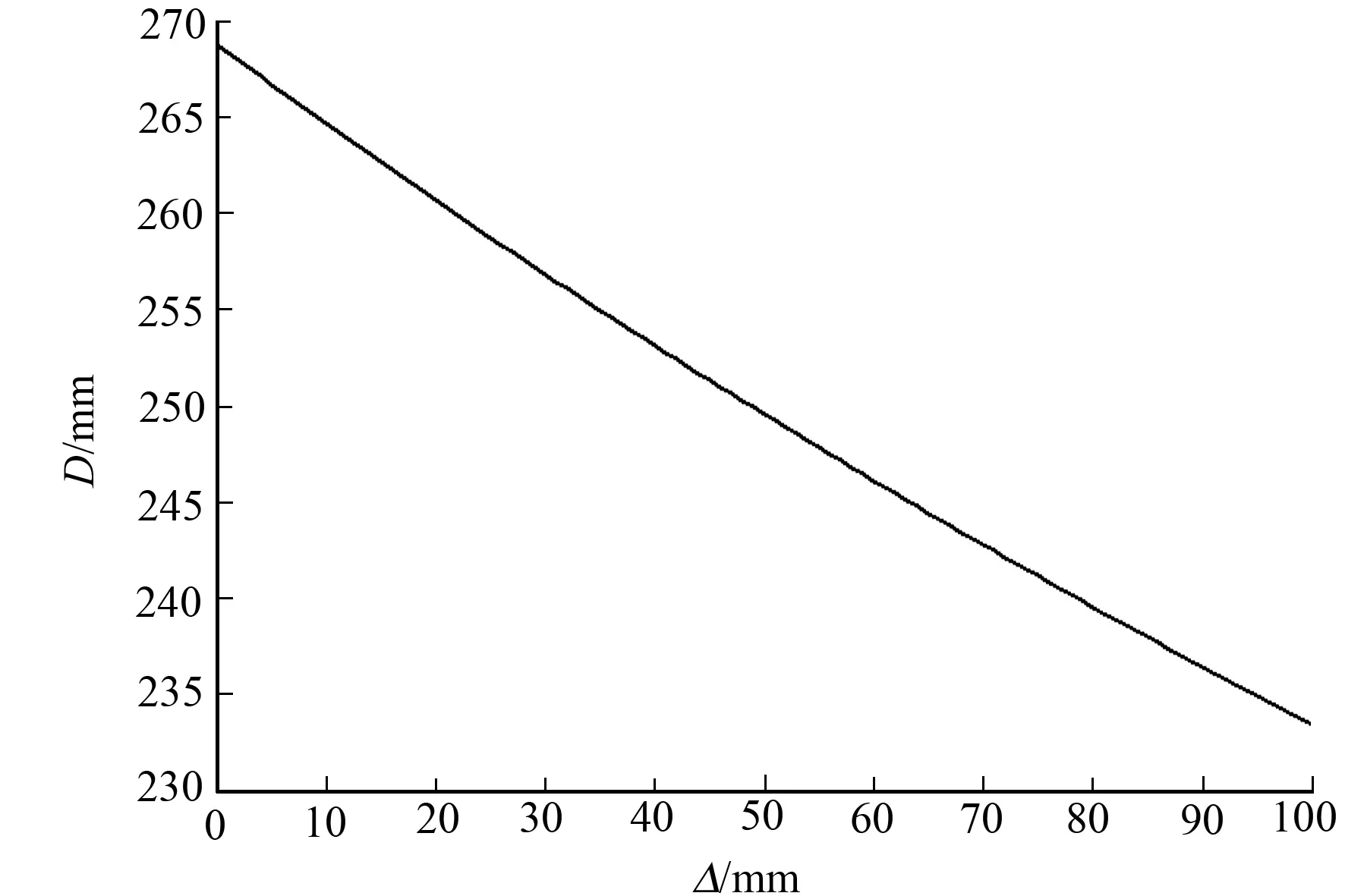
图2 位移-中径的关系图Fig.2 Displacement-medium diameter diagram

将图2中的位移扩展到弹簧的自由高度，其扩展的基本原理是,在对弹簧自由高度进行压缩时，其位移的距离是各圈之间的空隙距离.因此，应尽可能多在图2中取点，在每个点的位移值上加上螺旋弹簧的簧丝直径，与之对应的中径不发生改变.此时,所得到一一对应的点集所组成的曲线是弹簧中径与轴向高度的关系图.

2 模型的建立与载荷特性分析

由位移-中径关系图扩展可得到弹簧中径与轴向高度的关系曲线，即可绘制出弹簧的二维图，如图3所示.根据中径和弹簧高度的关系和弹簧基本参数，在Pro/E中建立中径和弹簧高度的函数曲线，并以此函数曲线为弹簧扫略路径，建模时设定簧丝直径d为定值20 mm.对绘制好的弹簧三维模型上下端切平处理，保证其总圈数和有效圈数,并将其导入ANSYS中进行载荷分析.

由于梁单元节点和单元数少，计算规模小,为设置接触单元方便，选择梁单元Beam 188 划分弹簧网格.接触采用三维梁接触单元Contact 176，与之对应的目标单元采用Target 171 单元，螺旋弹簧的自接触也采用同样的接触对单元.Contact 176 单元可设置螺旋弹簧的接触面大小，在分析过程中，得以准确模拟螺旋弹簧的接触[7].在分析过程中，边界条件设定为：在下端弹簧的底端加上固定约束，在上端弹簧上表面轴线方向施加法向载荷.由于螺旋弹簧特性的对称性，因此，只分析其压缩载荷下的位移情况，最终得到的应力云图及结构变形图，读取该载荷下的位移值，如图4所示.

图3 弹簧二维平面图(单位：mm) 图4 应力云图及结构变形图 Fig.3 2D plan of spring (unit: mm) Fig.4 Stress nephogram and structural deformation diagram

用同样的方法分别加载20个大小不同的载荷，最终得到的结果，如表3所示.表3中：F为载荷；Δ为位移量；Kc为刚度计算值.

利用MATLAB处理表3中的结果数据和拟合函数y1=polyfit(x，y，N)拟合得到载荷函数[8].根据经验，3次拟合已经可以达到很好的精度.因此,拟合过程中采用3次拟合，即

据此绘制拟合曲线，并与空气弹簧的位移-力的关系特性曲线作对比，如图5所示.

同理，拟合出刚度函数计算式为

据此绘制拟合曲线，并与空气弹簧的位移-刚度的关系特性曲线作对比，如图6所示.

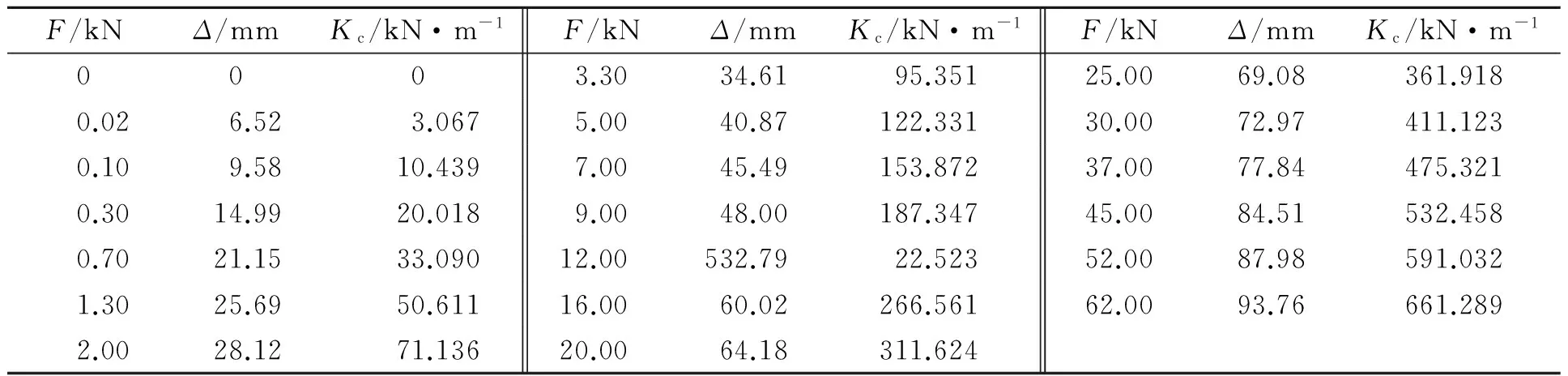
表3 有限元分析结果数据Tab.3 Finite element analysis results data

图5 位移-力的关系特性曲线对比图 图6 位移-刚度的关系特性曲线对比图Fig.5 Comparison chart of displacement- Fig.6 Comparison chart of displacement- force relation curve stiffness relation curve

由图5，6可知：经过拟合的弹簧特性曲线与空气弹簧相比存在一定误差.究其原因，可能有如下4个主要因素.

1) 相同位移下，所设计的非线性弹簧产生的力比空气弹簧大，且位移越大误差越大.即产生的原因有曲线拟合时有误差，弹簧高度-中径曲线离散取点在建三维模型时有误差，以及有限元分析结果数据拟合时存在误差等3个方面.

2) 所设计的非线性弹簧的刚度.在小位移下，与空气弹簧相比小，而在大位移下，与空气弹簧相比要大，且误差随着位移的增大而逐渐增大.

图7 四分之一汽车悬架系统简化模型Fig.7 Quarter of car suspension system simplified model

3) 所设计的非线性弹簧的刚度，在其自由高度时刚度为零，而空气弹簧则不为零.原因是由于橡胶的迟滞效应使空气弹簧的位移-刚度关系曲线左移，且空气弹簧充气后其表面已经存在压力.

4) 考虑到螺旋弹簧的对称性，其拉伸时的特性曲线相对其特性依然满足前面3个因素.

3 模型的建立及其仿真分析

3.1四分之一悬架模型的建立

所拟合的非线性弹簧作为悬架系统的一部分，在优化后应利用系统验证其性能，即优化与控制[9].因此,建立四分之一汽车悬架系统简化模型,如图7所示.基本参数如表4所示.表4中：Mse为座椅和驾驶员质量；Ms为四分之一悬架质量；Mu为四分之一非悬架质量；bs为车辆悬架阻尼比；bse为座椅悬架阻尼比；Ku为轮胎刚度；Ks为汽车悬架弹簧刚度；Kse为座椅悬架弹簧刚度.

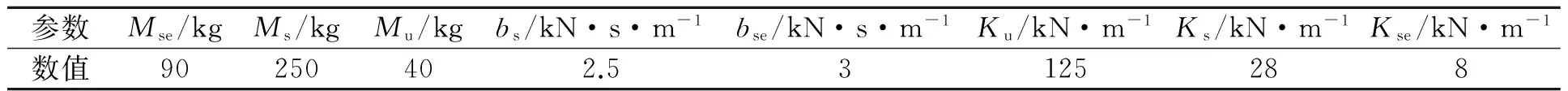
表4 汽车悬架系统简化模型的仿真参数值Tab.4 Simulation parameter value of automobile suspension system

根据受力分析可得驾驶员和座椅质量Mse运动方程[7].

簧上质量运动方程为

簧下质量运动方程为

式(8),(9)中:Zse,Zs,Zu分别表示座椅和驾驶员位移、四分之一悬架质量位移、非悬架质量位移;Mse,Ms,Mu分别表示座椅和驾驶员质量、四分之一悬架质量质量、非悬架质量质量;Kse,Ks,Ku分别表示座椅和驾驶员刚度、四分之一悬架质量刚度、非悬架质量刚度;bse,bs,bu分别表示座椅和驾驶员阻尼比、四分之一悬架阻尼比、非悬架质量阻尼比.

由于F是非线性的3次位移函数，文中使用的数学模型是建立在定刚度的基础上的，同时,为了简化建模的难度，因此,将其简化，即将其二次项和三次项分别线性化处理.

摄动定理又称小参数展开法，利用摄动法可以求解方程的渐进解.通常要将物理方程和定解条件无量纲化，在无量纲方程中选择一个能反映物理特征的无量纲小参数作为摄动量；然后，假设解可以按小参数展成幂级数，将这一形式级数代入无量纲方程后，可得各级近似方程.依据这些方程可确定幂级数的系数，对级数进行截断，便得到原方程的渐进解.由于初始时系统处于平衡位置，在考虑外界激励的情况下为简单起见不考虑整个方程的通解.利用摄动定理可以很好地将非线性微分方程展开的特点，可以得到式(8),(9)的解为

式(10)中:ζ为表示弹簧非线性度的参数；Z0，Z1，…，Zs0，Zs1，…，Zu0，Zu1等分别为式(10)各式的解.

将式(10)带入式(8),(9)，把式中各项的非线性项在Z0，Zs0，Zu0附近展开成ζ的幂级数并移到等式右边，比较ζ的系数可得

对比各项系数可求得z0,zs0,zu0,…,最终得到方程的解.此时，非线性方程可近似转换成线性方程.

3.2仿真分析

为了能真实地反映汽车在实际路面上行驶的状况，在Simulink中搭建的四分之一悬架仿真模型[10]，如图8所示.当路面输入为白噪声，其路面谱输入如图9所示.图9中：R为不平度.

图8 四分之一悬架仿真模型Fig.8 Simulation model of quarter of suspension

图9 用白噪声模拟的地面不平度Fig.9 Ground noise with white noise simulation

经过仿真，定刚度四分之一悬架模型与拟合非线性刚度四分之一悬架模型的各输出变化对比，如图10所示.图10中：a为车身加速度；Δ为车身位移.

(a) Zse (b) Zs

(c) 车身加速度 (d) 车身位移图10 非线性刚度悬架模型与定刚度悬架模型的仿真结果对比Fig.10 Comparison of simulation results of nonlinear rigidity suspension model and rigid rigidity suspension model

由图10(a)可知：座椅和驾驶员位移量随时间不断波动，位移波幅下降约50%，下降幅度明显，波峰增多.这说明对于随机输入的白噪声，非线性弹簧比定刚度弹簧有更好的减震效果，波峰增多说明对于同样的白噪声输入，其波动斜率减小.由图10(b)可知：对比非线性弹簧和定刚度弹簧簧上质量位移可以看出，其减震效果十分明显，波峰增多.由图10(c),(d)可知：车身加速度和车身位移量随时间波动，车身位移值，车身加速度相对下降且波动斜率减小.

仿真结果表明:非线性刚度悬架对白噪声输入时各指标出现振幅减小，波动斜率减小的情况，对振动具有更好的调节能力，从而提高了车辆的平顺性和舒适性.

4 结论

通过对空气弹簧的分析，找出空气弹簧刚度和位移的变化关系；然后，根据螺旋弹簧刚度的计算公式,得到弹簧中径与轴向高度的关系曲线.在ANSYS中对所建模型进行载荷分析，并对结果数据进行拟合，得到所设计弹簧的特性曲线方程.通过拟合得到的刚度特性曲线、力-位移特性曲线与空气弹簧相比存在一定误差，其主要表现为在小位移时所设计弹簧刚度比空气弹簧小，而在大位移时所设计弹簧刚度比空气弹簧大.

文中所设计的非线性螺旋弹簧为对应于空气弹簧在其某一内压下的非线性特性功能.通过建立四分之一悬架模型的动力学方程，利用摄动法将非线性弹簧特性曲线方程线性化，并在MATLAB/Simulink中对四分之一定刚度悬架和四分之一非线性刚度悬架进行了仿真分析.仿真结果表明：车身位移值、车身加速度、座椅和悬架位移量随时间波动，相对于定刚度弹簧波幅下降约50%.说明非线性刚度悬架对输入具有更好的调节能力.因此，利用空气弹簧的非线性特性所设计的非线性弹簧，可有效提高车辆的舒适性和平顺性.

[1] 陈璜，严世榕.汽车悬架的ADAMS仿真分析[J].机电技术，2014(1):16-18.DOI:10.3969/j.issn.1672-4801.2014.01.006.

[2] 郑松林，徐骏，高大威，等.车用变刚度螺旋弹簧最佳刚度特性曲线拟合与验证[J].现代制造工程，2015(12):6-11.DOI:10.3969/j.issn.1671-3133.2015.12.003.

[3] 严宏志，谭武中，韩奉林，等.变截面弹簧设计及其刚度特性分析[J].机械科学与技术，2014，33(2):298-302.

[4] 高扬，方宗德，祝小元，等.汽车囊式空气弹簧变刚度特性拟合分析[J].机械科学与技术，2014，33(1):113-116.

[5] 陈燎，周孔亢，李仲兴.空气弹簧动态特性拟合及空气悬架变刚度计算分析[J].机械工程学报，2010，46(4):93-98.DOI:10.3901/JME.2010.04.093.

[6] NIETO A J，MORALES A L，GONZLEZ A，etal.An analytical model of pneumatic suspensions based on an experimental characterization[J].Journal of Sound and Vibration，2008，313(1/2):290-307.DOI:10.1016/j.jsv.2007.11.027.

[7] 杨峰.基于ANSYS的汽车悬架螺旋弹簧限元分析[J].机械，2011，38(7):23-25.DOI:10.3969/j.issn.1006-0316.2011.07.006.

[8] 宋晓霞.基于MATLAB的通用数据拟合方法[J].山西大同大学学报(自然科学版)，2014，30(4):1-3.DOI:10.3969/j.issn.1674-0874.2014.04.001.

[9] 陈国卫，金家善，耿俊豹.系统动力学应用研究综述[J].控制工程，2012，19(6):5-12.DOI:10.3969/j.issn.1671-7848.2012.06.001.

[10] 唐志桥.二分之一车辆悬架系统的动力学仿真研究[J].公路与汽运，2015(1):5-8.DOI:10.3969/j.issn.1671-2668.2015.01.003.

[11] 秦娜娜，张井岗.二自由度控制方法研究[J].控制工程，2017，24(4):895-899.DOI:10.14107/j.cnki.kzge.15C2.0773.

[12] 赵研，方宗德，寇发荣.非线性汽车悬架系统建模与仿真研究[J].机械科学与技术，2006，25(4):484-486.DOI:10.3321/j.issn:1003-8728.2006.04.028.

[13] 李俊青，苏铁熊，史小航.基于MATLAB的主动悬架的最优控制分析[J].汽车实用技术，2012(2):32-34.

[14] 喻凡，林逸.汽车系统动力学[M].北京:机械工业出版社，2005.

(责任编辑： 钱筠英文审校： 崔长彩)

DesignandSimulationAnalysisofNonlinearCoilSpringforAutomobileSuspension

LI Jun， LI Xueyun

(School of Mechanical and Vehicle Engineering， Chongqing Jiaotong University， Chongqing 400074, China)

By fitting the characteristic curve of the air spring and using the formula of the coil spring stiffness, the relationship between the medium diameter and height of the coil spring was found. The load characteristics of the three-dimensional model were analyzed in ANSYS， and the result data was fitted to the characteristic curve equation of the designed spring. The dynamic equation of a quarter suspension model was established， the nonlinear coil spring characteristic curve equation was linearized by the perturbation method and then got into the dynamic equation. The simulation model was established in MATLAB/Simulink， and the results were compared with those of the quarter fixed stiffness suspension system. The simulation results show that the nonlinear coil spring designed by using the nonlinearity of the air spring can improve the sit comfort and ride comfort of vehicle， and the parameters of the variable stiffness are improved greatly.

automobile； air spring； nonlinear coil spring； suspension system； curve fitting

10.11830/ISSN.1000-5013.201706044

U 463.3

A

1000-5013(2017)06-0753-07

2017-06-17

李军(1964-)，男，教授，博士，主要从事汽车发动机排放与控制、节能与新能源汽车的研究.E-mail:cqleejun@163.com.

国家自然科学基金资助项目(51305472)； 重庆市工程技术中心科研基金资助(CSCT2015YFPT_GCJSYJZX011)； 重庆市重点实验室科研基金资助项目(CSCT2015YFPT-ZDSYS30001)