k-d类估计下数据删除模型的强影响分析

朱 宁，周桂兰

（桂林电子科技大学数学与计算科学学院，广西 桂林 541004）

k-d类估计下数据删除模型的强影响分析

朱 宁，周桂兰

（桂林电子科技大学数学与计算科学学院，广西 桂林 541004）

在k-d类估计下对单个数据删除模型进行研究，得到原模型(k，d)与数据删除(k，d)（i）、岭估计k之间的关系，并推导得到CRi统计量和Cook统计量新的表达形式.

k-d类估计；数据删除模型；CRi统计量；Cook统计量

0 引言

考虑一般线性模型：

其中y为n×1阶向量，X为n×p阶列满秩设计阵，β为p×1阶未知参数向量，ε为n×1随机误差向量，In为n阶单位矩阵.在线性模型（1）中，估计回归参数的最基本的方法是最小二乘法＝（X'X）-1X'Y，这个方法不仅在统计学中，在数学其它分支，如运筹学、计算数学和控制论等，都占有很重要的地位.但当设计阵X'X存在一个趋于零的特征值时，最小二乘估计不再是一个好的估计，此时估计参数的均方误差会很大.为了解决这个问题，很多学者在选择牺牲无偏的基础上提出了一系列新的估计，比较常用的估计有Hoerl和Kennard提出的岭估计（k）＝（X'X+kIp）-1X'Y、Stein估计、主成分估计、Liu估计、k-d类估计等[1]，但当数据存在异常值时，这些估计并不适应，为此把有偏估计和数据删除放到一起研究是有必要的.

韦博成[2]研究了最小二乘下的数据删除的强影响分析.魏传华、吴喜之[3]在空间分析中提出混合地理加权回归模型的删除模型，定义了数据删除模型参数分量的Cook统计量，讨论了均值漂移模型异常点的检验统计量．张莉莉，史建红[4]对SUR模型的影响分析进行研究，得到SUR模型和数据删除模型的两种近似似然距离公式.朱宁、黄黎平和严冠东[5-7]分别在岭型主成分估计和Stein岭型主成分估计下对单个数据和多个数据删除模型进行研究，讨论线性模型与数据删除模型的估计量之间的关系.

本文在Sakallıoĝlu S和Kaçıranlar S[8]所提出的k-d估计的基础上，结合数据删除模型的特点，对新的有偏估计下的数据删除模型的强影响问题进行研究，证明此有偏估计的相关性质，并在前人的基础上提出CRi统计量和Cook统计量新的表达形式，并用该统计量来判断强影响点.

1 两参数估计的相关性质

引理1[1]：在模型（1）下提出了未知参数β新的有偏估计，即在岭估计和Liu估计的基础上利用最小二乘的方法得到新的估计：

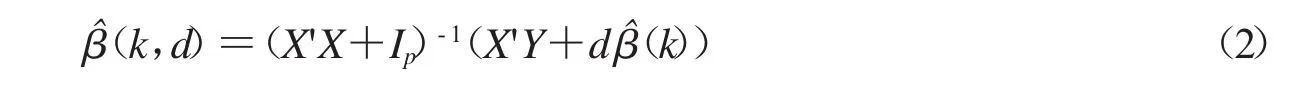
下面讨论数据删除模型与线性模型的估计量之间的关系.

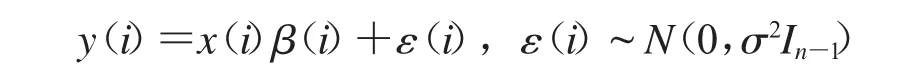
其中，y（i）为（n-1）×1阶观测，x（i）为（n-1）×p阶列满秩设计阵，β（i）为p×1阶未知参数向量，ε（i）为（n-1）×1随机误差向量，In-1为（n-1）阶单位矩阵.

其中Ip为p阶单位矩阵.

证明：为了方便后面的证明，公式（2）中的k-d估计可以变形为：

模型（2）中的k-d估计为：

[9]知，模型（2）的岭估计有如下关系：

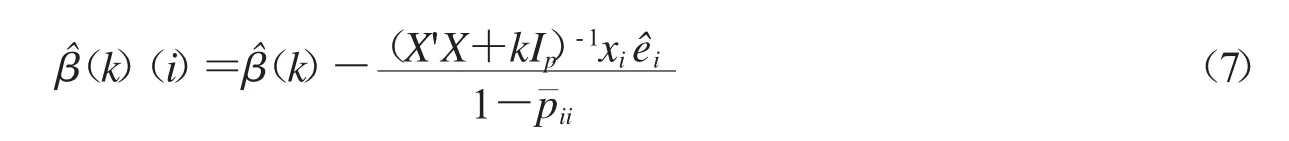
证明方法如定理1.

性质1：在线性模型y＝Xβ+ε，ε～N（0，σ2In）中，删除一组数据得到模型y（i）＝X（i）β（i）+ε（i），ε（i）～N（0，σ2In-1），若（k，d）（i）可表示删除模型中未知参数的值，则预测值可以表示为（k，d）（i）和yi的线性组合.

证明：

2 诊断统计量

2.1 协方差比统计量

估计量的方差是度量估计量优良性的重要统计量，而协方差比统计量[1]主要度量数据点（yi，x'i）对估计量的影响.由

定理3：在k-d估计下，协方差统比计量为：

证明：因为

引理2[2]：模型（2）y（i）＝X（i）β（i）+ε（i）中β和σ2的最小二乘估计与模型（1）中相应的估计和σ2有如下关系：

证明：由引理2可知

证毕.

2.2 Cook统计量

引理3[1]：Cook统计量的定义为：

定理4：k-d估计下的Cook统计量可表示成：

把上面的公式代入（8）式整理可得Cook统计量的表达式.

3 小结

在k-d类估计下，得到了数据删除下的k-d类估计与k-d类估计下原模型参数估计岭估计三者之间的关系，找出预测估计和yi、（k，d）（i）之间的线性表达式，并根据最小二乘估计下Cook统计量的表达式，推导出数据删除下k-d类估计的CRi统计量和Cook统计量新的表达形式.

参考文献

[1]王松桂，陈敏，陈立萍.线性统计模型：线性回归与方差分析[M].北京：高等教育出版社，1999.

[2]韦博成，鲁国斌，史建清.统计诊断引论[M].南京：东南大学出版社，1991.

[3]魏传华，吴喜之.混合地理加权回归模型的统计诊断[J].统计与信息论坛，2009，24（1）：9-13.

[4]张莉莉，史建红.半相依线性回归模型的影响分析[J].数学杂志，2010，30（1）：137-144.

[5]朱宁，黄黎平.岭型主成分估计下数据删除模型的强影响分析[J].统计与决策，2012（15）：72-74.

[6]朱宁，严冠东.Stein岭型主成分估计下的单个数据删除模型的研究[J].统计与决策，2015（14）：16-18.

[7]朱宁，严冠东，刘庆华.Stein岭型主成分估计下多个数据删除模型的强影响分析[J].汕头大学学报（自然科学版），2015，30（2）：20-27.

[9]钱峰，石丽娟.数据删除模型对于广义岭估计的影响[J].南通大学学报（自然科学版），2008，7（1）：75-78.

Strong Impact Analysis of Data Delete Model Based on k-d Class Estimation

ZHU Ning,ZHOU Guilan
（School of Mathematics and ComputingScience,Guilin Universityof Electronic Technology,Guilin 541004,Guangxi,China）

With the k-d class estimation,the single data deletion model is studied.The relationship among the original model,the data deletionridge estimateand derive the new form of CRistatistic and Cook statistic is obtained.

k-d class estimation;data deletion model;CRistatistic;Cook statistic

1001-4217（2017）04-0035-06

O212.1

A

2017-03-07

朱 宁（1957—），男，湖南宁乡人，教授，研究方向：线性统计模型.

周桂兰（1993—），女，广西南宁人，硕士究生，研究方向：应用统计.E-mail：839590076@qq.com.

广西自然科学基金项目（2016GXNSFBA380102）