两个新的双曲平均及其Schur幂凸性

何 灯，李云杰

（福建省福清第三中学，福建 福清 350315）

两个新的双曲平均及其Schur幂凸性

何 灯，李云杰

（福建省福清第三中学，福建 福清 350315）

定义了两个新的双曲函数及反双曲函数的复合平均，运用分析方法，研究了这两个平均的Schur幂凸性，给出了判定的充要条件.

Schur凸性；Schur幂凸性；双曲函数；反双曲函数

0 引言

2003年，《美国数学月刊》11031问题定义了如下“奇特”平均并提出一个相关的不等式猜想：

问题11031设x，y＞0，平均M（x，y）＝lnN（x，y），其中

求证或否定M（x，y）≤G（x，y）.

并通过证明sh（thx）是（0，+∞）上递增的几何凹函数而证明了上述猜想.

文献[3]研究了M（x，y）关于（x，y）在（0，+∞）2上的Schur-凸性和Schur-几何凸性.

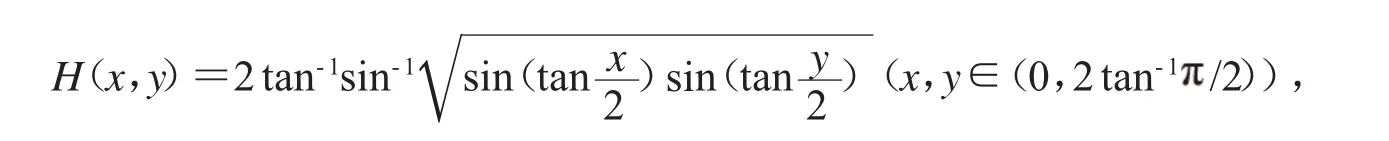
文献[4]定义了与M（x，y）相类似，且涉及三角函数及反三角函数复合的一个新的平均并借助于数值计算和多项式判别系统[5-6]，研究了M（x，y）及H（x，y）在各自定义域上更一般的性质--Schur幂凸性[7-11].

类似于M（x，y），本文定义如下两个新的双曲平均研究M1（x，y）、M2（x，y）关于（x，y）在（0，+∞）2上的Schur幂凸性，给出判定的充要条件.

1 定义和引理

对于x＝（x1，x2，…，xn）∈Rn，将x的分量递减重排后，记作x[1]≥x[2]≥…≥x[n].并用x≤y表示xi≤yi（i＝1，…，n）.

定义1[12]2设x，y∈Rn满足则称x被y所控制，记作x≺y.

定义2[12]54设Ω⊂Rn，φ:Ω→R，

（i）若在Ω上x≤y⇒φ（x）≤φ（y），则称φ为Ω上的增函数；若-φ是Ω上的增函数，则称φ为Ω上的减函数.

（ii）若在Ω上x≺y⇒φ（x）≤φ（y），则称φ为Ω上的Schur凸函数；若-φ是Ω上Schur凸函数，则称φ为Ω上Schur凹函数.

引理1[12]58设E（⊆Rn）是有内点的对称凸集，f:E→R为连续，且在E的内部intE可微，则f在E上为Schur-凸（凹）函数当且仅当f在E上对称，且对所有的x∈intE，都有定义3[1，13-14]设E⊆Rn++，对于任二向量x，y∈E，当（1nx1，1nx2，…，1nxn）≺（1ny1，1ny2，…，1nyn）时，都有f（x）≤f（y）成立，则称f是E上的Schur-几何凸函数；f为E上的Schur-几何凹函数，当且仅当-f为Schur-几何凸函数.

引理2[14]设为有内点的对称集，为凸集，f:E→R连续，且在intE内可微，则f为Schur-几何凸（凹）函数的充分必要条件是f在E上对称，且对所有的x∈intE，都有

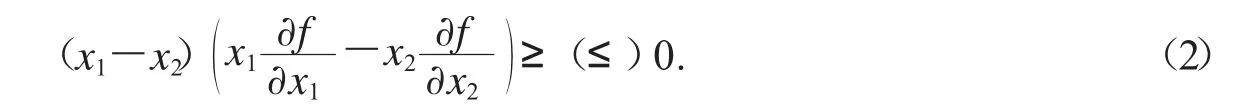
定义4[15-16]设若任取x，y∈E，当

时，都有f（x）≤f（y）成立，称f为E上的Schur-调和凸函数；若-f是E上Schur-调和凸函数，则称f为E上的Schur-调和凹函数.

引理3[16]设为有内点的对称集，为凸集，f:E→R连续，且在intE内可微，则f为E上的Schur-调和凸（凹）函数的充分必要条件是f在E上对称，且对于任意x∈intE，都有

定义5[7-11]（i）设f:R++→R是严格单调函数，Ω⊂Rn.若对于任何x，y∈Ω，总有f-1（αf（x）+βf（y））∈Ω，则称Ω是f-凸集，其中α，β∈[0，1]且α+β＝1.

（ii）设Ω⊂Rn，Ω内部非空.φ:Ω→R，对于任意x，y∈Ω，若f（x）≺f（y）时，有φ（x）≤φ（y），则称φ为Ω上的Schur-f凸函数；若-φ是Ω上Schur-f凸函数，则称φ为Ω上Schur-f凹函数.

由Schur-f凸函数的定义知，若g为单调递增（减），g（φ（x））有意义，则φ为Schur-f凸函数，当且仅当g◦φ为Schur-f凸（凹）函数.

定义6[7-11]在定义5中若取则称φ为Ω上的Schur-m阶幂凸函数；若-φ是Ω上Schur-m阶幂凸函数，则称φ为Ω上Schur-m阶幂凹函数.

引理4[7-11]设f:R→R是严格单调的可微函数，是有内点的对称f-凸集，φ:Ω→R于Ω上连续，在Ω的内部Ω0可微，φ是Ω上Schur-f凸（Schur-f凹）的充要条件是φ在Ω上对称，且对于∀x∈Ω0，有

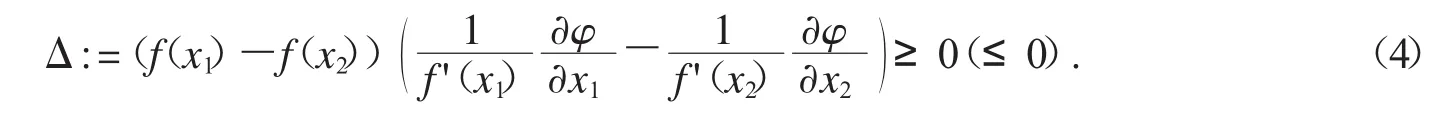
对于Schur-m阶幂凸函数，若m≠0，相应的Schur条件为

不难发现，式（4）综合了式（1）（2）（3）（5）.

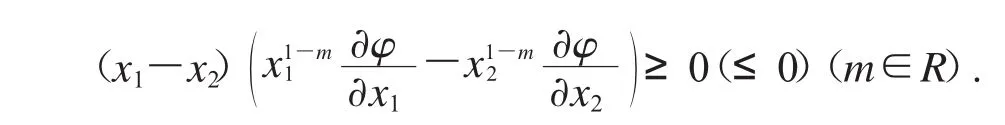
引理5[17]设a≤b，u（t）＝tb+（1-t）a，v（t）＝ta+（1-t）b，1/2≤t2≤t1≤1或0≤t1≤t2≤1/2，则

证明

由不等式thx＜x（x∈（0，+∞））可得

由于（thx）'＝1-th2x＞0，故g3（x）＝thx关于x在（0，+∞）上单调递增，结合不等式chx＞1及shx＞x（x∈（0，+∞））可得

2 主要结果及证明

定理1 M1（x，y）关于（x，y）在（0，+∞）2上Schur-m阶幂凹当且仅当m≥1.证明

当m≥1，y1＝x1-m关于x在（0，+∞）上单调递减，结合引理6得关于x在（0，+∞）上单调递减，则F2（x，y）≤0，从而ΔM1（x，y）≤0，由引理4得M1（x，y）关于（x，y）在（0，+∞）2上Schur-m阶幂凹.

当m＜1，由于

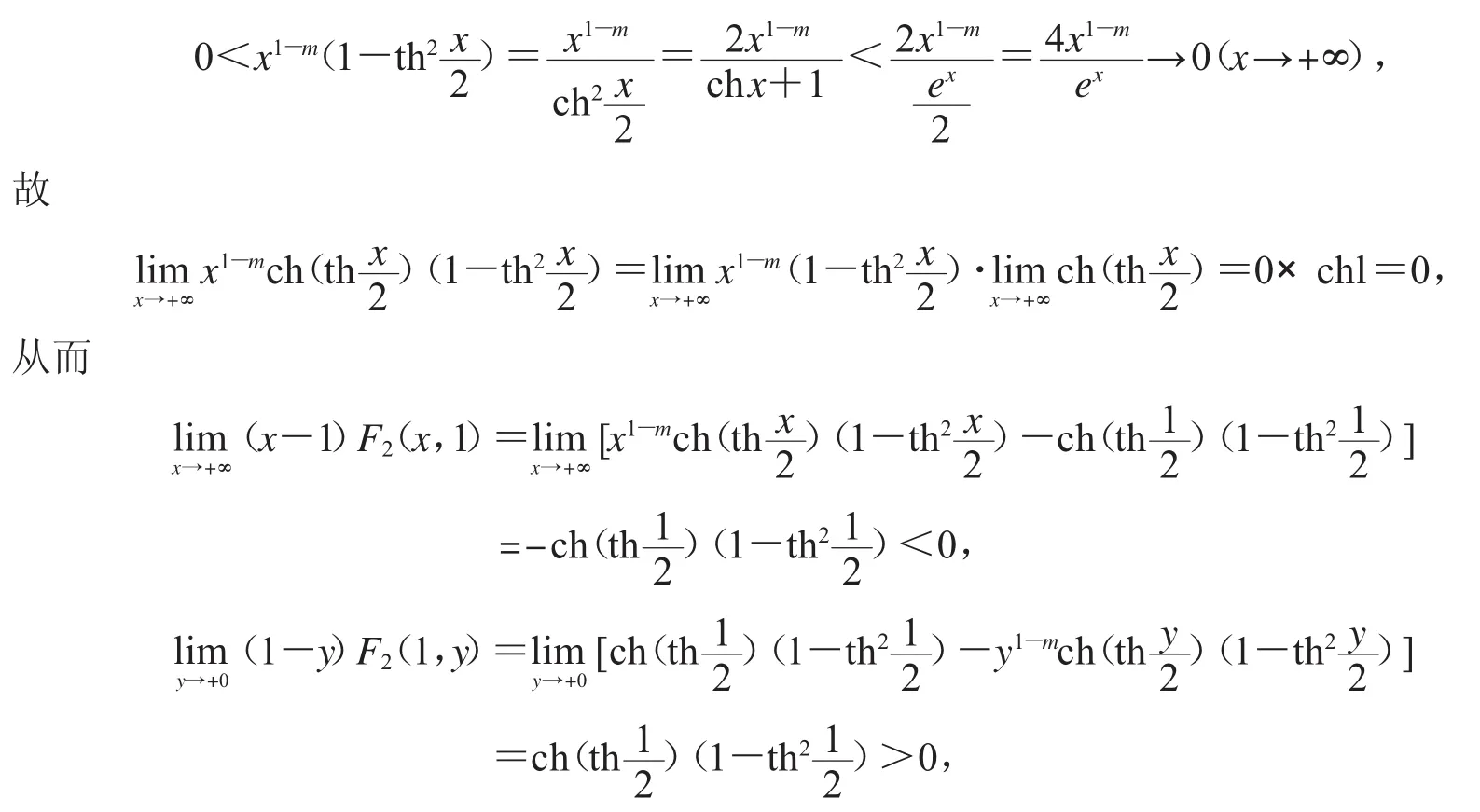
显然F2（x，y）在（0，+∞）2上符号不恒定，则ΔM1（x，y）在（0，+∞）2上符号不恒定，从而当m＜1时M1（x，y）不是（0，+∞）2上Schur-m阶幂凹（凸）函数.

综上，定理1得证.

令定理1中m＝1可得

推论1 M1（x，y）关于（x，y）在（0，+∞）2上为Schur-凹函数.

由推论1并结合定义2及引理5可得

推论2 对于（x，y）∈（0，+∞）2，x≤y，1/2≤t2≤t1≤1或0≤t1≤t2≤1/2，有

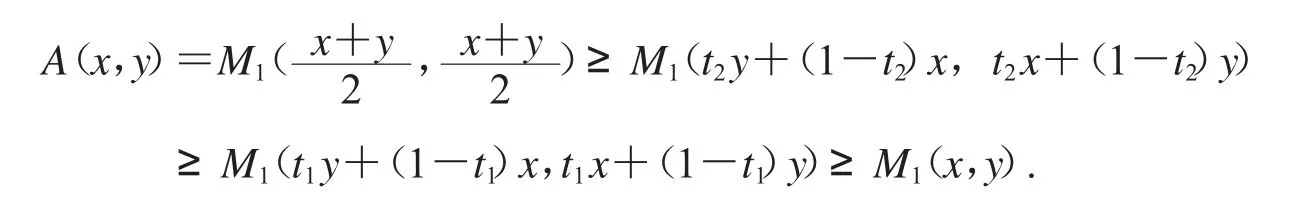
定理2M2（x，y）关于（x，y）在（0，+∞）2上Schur-m阶幂凹当且仅当m≥1.证明

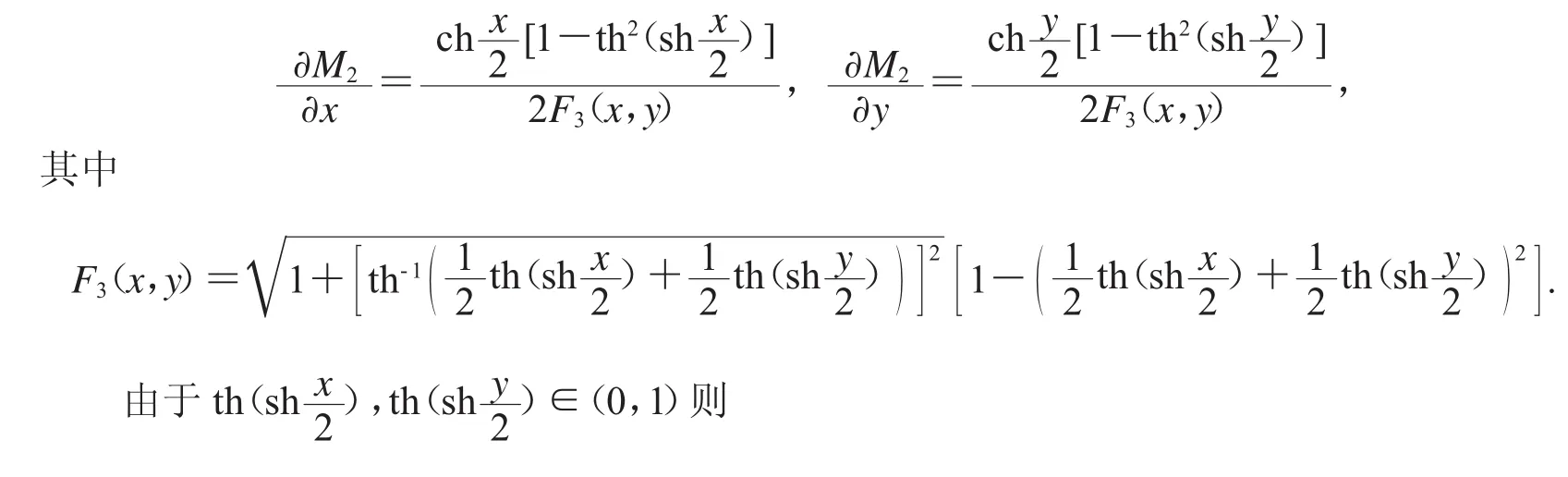
故F3（x，y）＞0.

显然F4（x，y）在（0，+∞）2上符号不恒定，则ΔM2（x，y）在（0，+∞）2上符号不恒定，从而当m＜1时M2（x，y）不是（0，+∞）2上Schur-m阶幂凹（凸）函数.

综上，定理2得证.

令定理2中m＝1可得

推论3 M2（x，y）关于（x，y）在（0，+∞）2上为Schur-凹函数.

由推论3并结合定义2及引理5可得

推论4对于（x，y）∈（0，+∞）2，x≤y，1/2≤t2≤t1≤1或0≤t1≤t2≤1/2，有

[1]张小明.几何凸函数[M].合肥：安徽大学出版社，2004：107-121.

[2]李大矛，石焕南.一个二元平均值不等式猜想的新证明[J].数学的实践与认识，2006，36（4）：278-283.

[3]石焕南.受控理论与解析不等式[M].哈尔滨：哈尔滨工业大学出版社，2012：283-287.

[4]何灯.关于两个“奇特”平均的Schur幂凸性[J].广东第二师范学院学报，2016，36（3）：30-38.

[5]杨路，张景中，侯晓荣.非线性代数方程组与定理机器证明[M].上海：上海科技教育出版社，1996：137-166.

[6]杨路，夏壁灿.不等式机器证明与自动发现[M].北京：科学出版社，2008：33-46.

[7]YANG ZH.SchurpowerconvexityofStolarskymeans[J].PublMath Debrecen，2012，80（1/2）：43-66.

[8]张小明.几个n元平均的积的Schur-阶幂凸性[J].湖南理工学院学报，2011，24（2）：1-6+13.

[9]YANG Z H.Schur power convexity of Gini means[J].Bull Korean Math Soc，2013，50（2）：485-498.

[10]YANG Z H.Schur power convexity of Daróczy means[J].Math Inequal Appl，2013，16（3）：751-762.

[11]邓勇平，吴善和，何灯.关于广义Muirhead平均的Schur幂凸性[J].数学的实践与认识，2014，44（5）：255-268.

[12]王伯英.控制不等式基础[M].北京：北京师范大学出版社，1990.

[13]张小明，续铁权.广义SCHUR-几何凸函数的定义及其应用[J].青岛职业技术学院学报，2005，18（4）：60-63.

[14]张小明，褚玉明.解析不等式新论[M].哈尔滨：哈尔滨工来出版社，2009：93-94.

[15]GUAN K Z.Schur-convexity of the complete symmetric function[J].Math Inequal Appl，2006，9（4）：567-576.

[16]GUAN K Z.Some properties of a class of symmetric functions[J].J Math Anal Appl，2007，336（1）：70-80.

[17]李大矛，顾春，石焕南.Heron平均幂型推广的Schur凸性[J].数学的实践与认识，2006，36（9）：387-390.

Two New Hyperbolic Averages and Their Schur Power Convexity

HE Deng,LI Yunjie
（Number 3 Middle School,Fuqing350315,Fujian,China）

The complex average of two hyperbolic function and inverse hyperbolic function is defined.The Schur power convexity of those two mean is studied by using the analytical method. The necessary and sufficient conditions for the judgment are given.

Schur convexity;Schur power convexity;hyperbolic function;inverse hyperbolic function

1001-4217（2017）04-0041-07

O178

A

2017-03-29

何 灯（1984—），男，福建福清人，学士，中学教师，全国不等式研究会成员.研究方向：解析不等式及不等式机器证明.E-mail：hedeng123@163.com