拨开图形变幻的迷雾
——苏科版数学八(下)“9.4正方形的判定和性质”案例研究
■顾明新
拨开图形变幻的迷雾
——苏科版数学八(下)“9.4正方形的判定和性质”案例研究
■顾明新
新课程强调学生学习的自主性和独立性,而数学的教学过程就是学生探究数学知识、发现数学规律、建构知识体系的过程。课堂要多为学生提供自主学习、自我展示、探究学习的舞台,教师的角色扮演则是课堂高效的关键。教师要善于通过营造和谐融洽的课堂氛围,调动学生的积极情态,引导他们最广泛地参与整个学习、讨论、合作交流的过程,鼓励他们大胆设想、发散思维、敢于实践、勇于创新,从而使不同层次的学生都能获得成功的体验以及进步和自信。深度探究更是突出学生在课堂中的主体地位,以改变学生的学习方式为着眼点,变被动学习为主动探究,使学生在分析问题和解决问题的过程中学会深入思考,学会思辨,进而提升学习的质量,提高解决问题的综合能力。现以苏科版数学八(下)“9.4正方形的性质和判定”的教学片段为例,剖析深度探究在课堂教学及学生思维中的促进作用。
一、合理引入,使深度探究有抓手
师:同学们,我们已经学习了平行四边形中的两类特殊四边形——矩形和菱形,研究了它们的性质和识别方法。今天,我们来进一步研究一种更为特殊的平行四边形,你们觉得是什么图形呢?
生:正方形。
师:正方形特殊在哪里呢?它具有什么特殊性质呢?
设计意图:教师根据师生交流的内容,在PPT中显示相应主题和图形。通过唤醒旧知识,实现向新知识的过渡。学生回顾矩形和菱形的定义、性质及识别方法,一方面再次固化了已有知识,另一方面为类比学习新知识做好了准备。仔细观察图形特征和几何元素变化是获得信息的前提。归纳总结出正方形的定义,教师通过问题情境引入,探究目的明确,给学生设置了展示智慧和才华的机会。在展示过程中,让学生养成仔细观察、严谨思考、表现自我的习惯,提高语言表达和自主探究、归纳总结的能力。
适合的有深度的探究学习是新课程理念所倡导的学与教的方式。教学中,教师坚持“一切以学生发展为本”的教育理念,根据学生的学习能力和教学需求,设置与学习者知识最近发展区要求一致的问题,通过适宜的方法引导他们观察思考、自主探究,发现数学一般规律,归纳总结新探究的知识点,从而提高课堂的教学效果,培养学生数学学习的兴趣,形成自主发现问题、探究问题、解决问题的良好思维品质。
二、有效深化,使深度探究有梯度
师:同学们,平行四边形或矩形或菱形或一般四边形,要具备什么条件才是正方形呢?我们如何识别正方形呢?
在画图尝试、独立思考及小组合作的基础上,学生初步厘清了“平行四边形—矩形(或菱形)—正方形”的变化过程。其中,对“对角线相等且互相垂直平分的四边形是正方形”的认识是一个曲折的过程,先是由优秀学生发现,并被其他学生验证认可,从而成为本节课学生智慧结晶的一个亮点。
师生共同梳理得出如下的知识结构示意图:
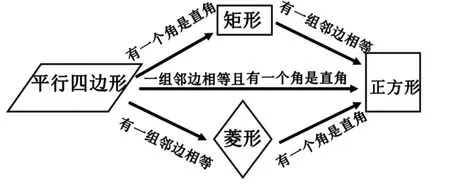
设计意图:在学生自主探究出正方形定义后,教师趁热打铁,创设问题链,让学生进一步深入探究正方形的识别方法。由于教材中除定义外,并没有给出具体的正方形的识别方法,所以该问题具有较强的开放性与挑战性。因此,采用小组合作探究是合适有效的方法。学生就边、角、对角线等维度开展分析、讨论后,教师适时给予肯定、赞许,以增强其交流分享的自信心。同时,应注重数学思想方法的渗透,“转化化归”“从特殊到一般”“分类讨论”等数学思想方法的灵活运用,让学生虽身处纷繁复杂的图形变幻之中,却能去繁化简,拨云见日,感受图形变化之美。
三、反思提炼,使深度探究显内涵
师:我们类比矩形、菱形的研究方法以及利用对称性,知道了正方形的边、角、对角线所具有的性质,那么平行四边形、矩形、菱形与正方形之间存在怎样的关系呢?
师:正方形是矩形吗?正方形是菱形吗?正方形是平行四边形吗?
通过师生交流得出平行四边形、矩形、菱形与正方形之间关系示意图。
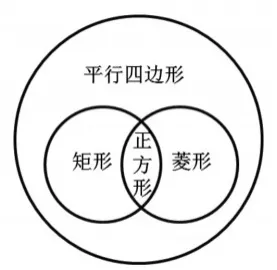
设计意图:厘清平行四边形、矩形、菱形与正方形之间的关系,有助于深度认识和理解这几种特殊四边形的区别与联系。得出结论的过程中,要尽可能让学生先独立思考,再合作交流。在整个教学活动中,教师仅发挥组织者、引导者的作用。教师抛出问题后,学生自主探究,自主总结,探索相关知识,深刻体会正方形的特殊性。教师把课堂的主动权还给学生,学生自己学习,自己设问,自己解决问题。当遇到困难,思考无法再深入时,教师才介入,或给予方法上的指导,或给予精神上的鼓励。这种学生之间互教、互助、互学的方式,为学生个性潜能的发挥提供“催化剂”,使学生“好学”“乐学”。
四、反馈评价,使深度探究得固化
设置一组包含填空、选择及说理的题目。(题目略。)
设计意图:通过有层次的练习反馈,让学生更加清楚地辨析几种特殊平行四边形概念间的区别与联系,理解特殊与一般的关系,及时巩固所学知识,提升探究质量,使深度探究得到巩固。同时,通过反馈训练、探究互评,提高学生分析问题、解决问题的水平,发展逻辑推理能力。在反馈评价中,学生的差异性是存在的,有些体现在对基础概念的理解上,有些体现在对综合知识的运用上,有些体现在对逻辑的推理上……教师根据反馈情况,进行有针对性地点评、辅导及补救,让学生在纠错的过程中进一步强化认识和理解,让不同层次的学生都能有所收获。
《义务教育数学课程标准(2011年版)》指出:“推理能力的发展应贯穿于整个数学学习过程中。推理是数学的基本思维方式,也是人们学习和生活中经常使用的思维方式。”推理在数学中具有重要的地位,是最基本的数学思想。平行四边形与矩形、菱形、正方形都是特殊的四边形,这些图形的性质、判定及运用是几何中的重要内容,是培养学生逻辑意识和推理能力的有效素材。教学中,引导学生采取深度探究的方式,不断提高学生探究的积极性和主动性,有利于学生对学习内容的认识和理解,有利于学生在今后数学学习方式上的转变,有利于学生的可持续成长与发展。
(作者为庞彦福名师工作室成员,无锡市雪浪中学副校长)
领衔人点评:推理是数学的基本思维方式,也是人们学习和生活中经常使用的思维方式。包括正方形在内的特殊平行四边形的性质、判定与运用是几何教学的重要内容,是促进学生推理能力螺旋上升的有效途径。教师要学会合理设计教学,善于经营课堂,不断提升教学水平。

