聚焦常见的函数模型及应用

■天津市南开中学高二(1 3)班 李稀琰

聚焦常见的函数模型及应用

■天津市南开中学高二(1 3)班 李稀琰

解决函数模型的关键有两点:一是实际问题数学化,即在理解的基础上,通过列表、画图,引入变量,建立直角坐标系等手段把实际问题翻译成数学问题,把文字语言翻译成数学符号语言。二是对得到的函数模型进行解答,得出数学问题的解,要注重数学能力的培养。

一、构建二次函数模型

例1 某商场出售某种商品,每天可卖1000件,每件获利4元。据经验,若每件少卖1角钱,则每天可多卖1 0 0件,问:每件应减价多少元,才能获得最大利润?

解析:设每件少卖x角钱,每天利润为y元,依题意得y=(10 0 0+1 0 0x)(4-0.1x)=-1 0x2+3 0 0x+40 0 0=-1 0(x-1 5)2+62 5 0,当x=1 5时,y有最大值。

二、构建分段函数模型

例2 通过研究学生的学习行为,专家发现,学生的注意力随着老师讲课时间的变化而变化,讲课开始时,学生的兴趣激增;中间一段时间,学生保持较理想的状态,随后学生的注意力开始分散。设f(t)表示学生注意力随时间t(分钟)的变化规律,f(t)越大,表明学生注意力越集中,经实验分析得知:

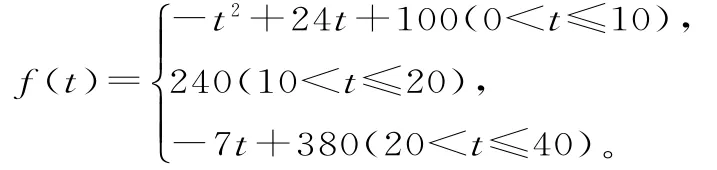
(1)问:讲课开始多少分钟,学生的注意力最集中?能持续多少分钟?

(2)讲课开始后5分钟与讲课开始后2 5分钟比较,何时学生的注意力更集中?

(3)一道数学难题,需要讲解2 4分钟,并且要求学生的注意力至少达到1 8 0,那么经过适当安排,老师能否在学生达到所需的状态下讲完这道题目?

解析:(1)当0＜t≤1 0时,f(t)=-t2+2 4t+1 0 0是增函数,当1 0＜t≤2 0时,f(t)=-t2+2 4t+1 0 0是减函数且f(1 0)=f(2 4)=2 4 0,所以讲课开始1 0分钟,学生的注意力最集中,能持续1 0分钟。

(2)求函数值比较,f(5)=1 9 5,f(2 5)=2 0 5,讲课开始后2 5分钟比讲课开始后5分钟学生的注意力更集中。

(3)当0＜t≤1 0时,f(t)=-t2+2 4t+1 0 0=1 8 0,得t=4。当2 0＜t≤4 0时,f(t)=-7t+3 8 0=1 8 0,得t=2 8.5 7,则学生注意力在1 8 0以上所持续的时间为2 8.5 7-4=2 4.5 7＞2 4,所以,经过适当的安排,老师可以在学生达到所需要的状态下讲授完这道题。

三、构建指数函数模型

例3 某林场现有木材3万立方米,如果每年平均增长5%,问:大约经过多少年该林场的木材量可增加到4万立方米?

解析:经过x年,木材量y=3(1+5%)x,由题意得3(1+5%)x=4,即1.0 5x=,两边同取常用对数得

四、构建无理函数模型

例4 某自来水厂的蓄水池中有4 0 0吨水,水厂每小时可向蓄水池注水6 0吨,同时蓄水池又向居民小区供水,t小时内供水为1 2 0 6t吨(0≤t≤2 4)。

(1)多少小时后蓄水池中的水量最少?

(2)若蓄水池中水量少于8 0吨时,就会出现供水紧张现象,请问:每天有几小时出现这种现象?

解析:(1)设t小时后蓄水池水量为y吨,则y=4 0 0+6 0t-1 2 0 6t(0≤t≤2 4)。令x=6t,0≤x≤1 2,则y=4 0 0+1 0x2-1 2 0x=1 0(x-6)2+4 0,当x=6,即t=6时,y有最小值4 0吨,所以供水6小时,水池中的水最少为4 0吨。

(2)由4 0 0+1 0x2-1 2 0x＜8 0,解得0＜x＜4,即0＜＜4,解得故每天有8小时供水紧张。

(责任编辑 刘钟华)