基于误差逼近器的巡航飞行器反步控制*

虞棐雄 王永超 曹立佳 张胜修 扈晓翔

火箭军工程大学，西安 710025

基于误差逼近器的巡航飞行器反步控制*

虞棐雄 王永超 曹立佳 张胜修 扈晓翔

火箭军工程大学，西安 710025

针对巡航飞行器在飞行过程中系统特征及各项参数时变、对控制系统强非线性的情况，设计了一种以反步法为基础的误差逼近鲁棒非线性系统。首先，对巡航飞行器建立6-DOF非线性模型，根据反馈线性理论，将系统转化为含有误差项的严格反馈MIMO系统。其次，利用Backstepping设计控制律和误差逼近律，在虚拟控制律设计中引入动态面法来避免多重微分运算，以解决“项数膨胀”问题。最后，运用Lyapunov稳定性定理证明了闭环系统有界且跟踪误差指数收敛于零的一个邻域内。通过飞行器飞行仿真，结果表明控制器在外界未知干扰下具有很强的稳定性和鲁棒性。

误差逼近器；MIMO系统；反步法；动态面；巡航飞行器

远程巡航飞行器是一个复杂的动力学系统。由于飞行距离远、飞行环境复杂，在飞行过程中飞行器的系统特性会发生变化。作用在飞行器上的空气动力与飞行器几何形状、飞行状态参数乃至飞行环境都呈现非常复杂的非线性关系。近年来，针对远程巡航飞行器这样的强非线性系统的控制问题有了一系列研究成果，例如动态逆[1]、反步法(Backstepping)[2]等直接面向非线性系统进行设计的非线性控制技术被广泛应用到飞行器控制方法的研究中。尤其是基于Lyapunov稳定性理论的反步法控制技术，因其具有快速收敛性和良好的鲁棒性，在飞行器控制系统中得到越来越多的应用。

反步法(Backsteeping)由Kokotovic等人在1991年首次提出，解决了长期以来具有纯反馈形式的非线性系统控制器设计和稳定性分析的难题。Backstepping实际上是一种由前向后递推的方法，所以又称逐步递推法。Sharma等[3-5]采用反步法分别设计了拦截导弹和飞机的综合控制系统；Sonneveldt[6]和朱铁夫[7]等则将这一技术应用在多操纵面推力矢量飞机的超机动飞行控制上；Harkegard等[8]提出了直接面向飞行器向量形式动态模型进行反步法控制器设计的方法。但是传统的反步法在控制器设计过程中需要对虚拟控制器反复求导，容易导致计算量随着阶数的增加而呈现指数增长，出现“计算膨胀”问题，从而给控制器的设计造成不便。针对这一问题，Swaroop等人[9]提出了动态面控制法，其核心是在每一步设计中引入积分滤波器，令所设计的虚拟控制律输入通过该滤波器，避免了每一步中对虚拟控制律的求导，从而解决了“计算膨胀”问题，简化了设计过程。另外，考虑飞行器遭遇较大的突发变化时，单纯的反步法不能很好地应对[10]。面对这一类不确定性问题，采用逼近器在线逼近不确定性是一种较好的选择。文献[11]研究了利用干扰观测器消除系统不确定性和未知外部干扰，并成功地应用于倒立摆和飞行器的控制中。

本文以远程巡航飞行器为研究对象，假设飞行器是存在未知外部干扰的MIMO系统，通过建立巡航飞行器模型，将其转化为含有未知不确定性的严格反馈系统，引入误差逼近器对未知干扰进行逼近，基于Backstepping和动态面进行控制器设计，最后利用Lyapunov 理论分析了所提控制方案的稳定性。

1 飞行器非线性模型

以巡航飞行器作为研究对象，在相关文献假设[12]的基础上，建立了其在飞行条件下的6-DOF非线性动态模型，可表示为

(1)

(2)

(3)

(4)

(5)

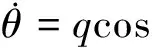
(6)

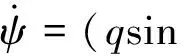
(7)

(8)

(9)

(10)

式中，Ix，Iy，Iz分别为各轴向转动惯量；Ixz为转动惯性积。

针对飞行器非线性动态模型，考虑选取角度状态变量x1，角速度状态变量x2，建立飞行器的非线性系统，即：

(11)

本文的控制目的是使系统能有效稳定跟踪控制指令x1d=[αd,βd,μd]。

在设计飞行控制器前，需要一些假设、定义和定理，通过分析改进，放宽要求。

假设1 参考指令足够光滑，其一阶和二阶导数均存在且有界。即存在已知的正常数bM，满足如下不等式：

值得一提的是，在实际跟踪控制指令信号中，指令信号通常都是有界的。将参考指令进行二阶滤波获得新的参考指令，目的是使其一阶和二阶导数均存在且有界。

对于与类似假设2的说法，在很多研究中普遍采用，如文献[14-15]。Lee等[15]对控制尾舵变化导致气动力改变进行了分析研究，结果表明这一影响可以忽略。通常情况下，当气动控制舵的有效面积相比气动力的主要来源——主翼和载体的有效面积较小时，这一假设是成立的。而本文研究的正是这一情况。另外，本文还引入了误差项，也可以将控制尾舵产生的气动力影响折合到误差估计中。

最终，在以上前提条件下，飞行器非线性模型 (式 (11))可以转化为MIMO纯反馈系统

(12)

式中，u为系统控制律输入。

2 控制器设计

针对MIMO纯反馈系统式(12)，反步控制器的设计过程如下：

步骤1：考虑系统式(12)的第1个子系统

(13)

(14)

(15)

式中，k1为正的控制器参数；r1为常数；λ1为控制器设计参数；同时，tanh(·)为双曲正弦函数。

步骤2：考虑系统式(12)的第2个子系统

(16)

系统式(16)的控制律选取为

(17)

式中，k2为正的控制器参数；λ2为控制器设计参数。

(18)

式中，r2为常数。

(19)

(20)

式中，τgt;0为滤波时间常数。

(21)

图1为控制器结构示意图。

图1 误差逼近反步控制器设计过程

3 稳定性分析

3.1 跟踪误差动态

由于系统指令跟踪控制的稳定性分析过程与系统跟踪动态有关，下面先讨论系统的跟踪误差动态。

(22)

(23)

(24)

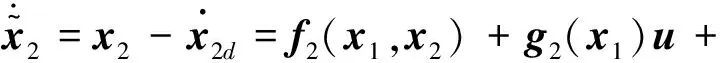
(25)

又因滤波器式(20)必然存在滤波误差，下面选取其滤波误差为

(26)

对z求导，可得

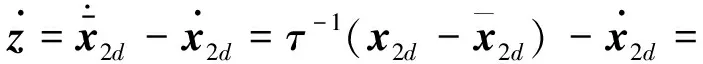
(27)

根据式(24)和(26)，可得

(28)

则跟踪误差动态式(23)变换为

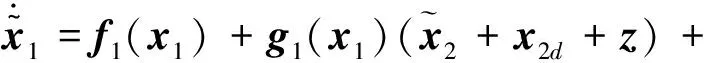
(29)

3.2 Lyapunov稳定性分析

研究系统稳定性时，选择如下所示的Lyapunov函数

(30)

式中，rigt;0为常数。

则V(t)对时间的导数为

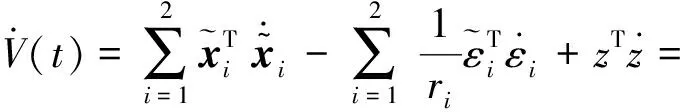
(31)

引入定理1[18-19]：对于∀xgt;0，有|x|-xtanh(x/λ)≤0.2785λ=λ′始终成立。

(32)

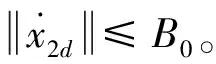
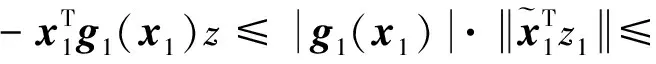
(33)

(34)

(35)

(36)

根据以上控制器设计和稳定性证明，可以得到定理1 ：对于满足假设1和2，并且存在外界干扰的非线性系统(11)，设计如式(21)所示的控制律以及如式(15)和(18)所示的误差逼近律，能够使闭环系统内的所有信号半全局最终一致有界(SGUUB)；并且选择合适的设计参数能使跟踪误差收敛到原点的一个很小领域内。

4 仿真结果与分析

以模型巡航飞行器为控制对象，采用本文设计的控制律和误差逼近律，通过仿真对飞行器的控制效果进行检验。

选择仿真的初始条件如表1所示。仿真采样时间为1ms，状态变量延迟为一个采样周期。

为了验证控制系统的鲁棒性，仿真中在原来模型的基础上对气动参数随机摄动40%，转动惯量随机摄动20%来模拟系统未知的不确定性。

飞行控制器的参数分别选取为：k1=6，k2=4，τ=0.01。误差逼近器的参数分别选取为：r1=2，r2=3。

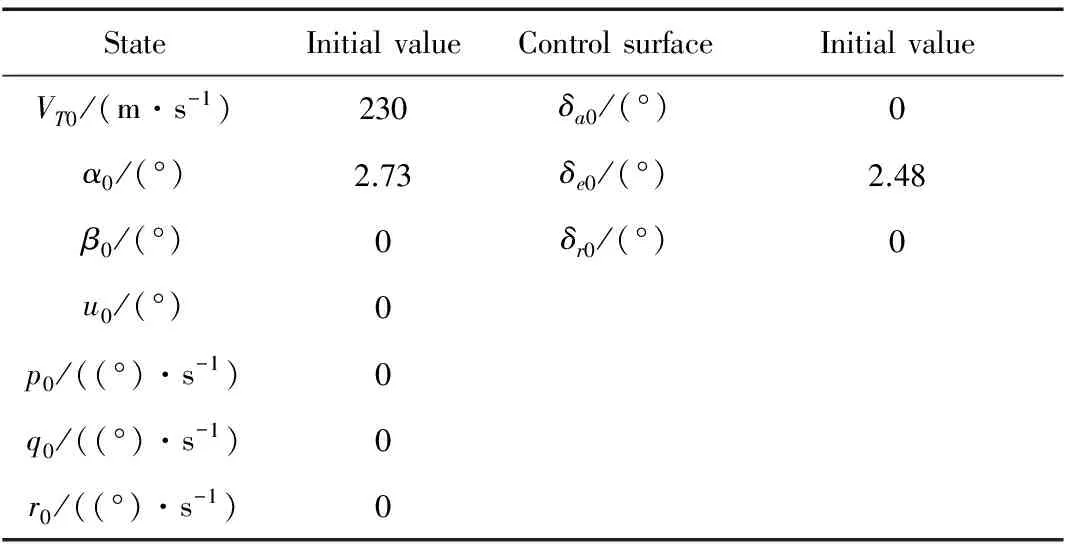
表1 仿真初始条件

图2～10给出了在Matlab中进行的6-DOF巡航飞行器飞行仿真图。需要指出，方法1表示设计反步控制器过程中引入误差逼近器，方法2表示设计反步控制器过程中未引入误差逼近器。另外，图2～ 4为2种方法的跟踪效果对比，图5～ 10为系统在设计反步控制器中引入误差逼近器后各角速度和虚拟舵偏角的变化情况。

图2 攻角指令跟踪对比结果

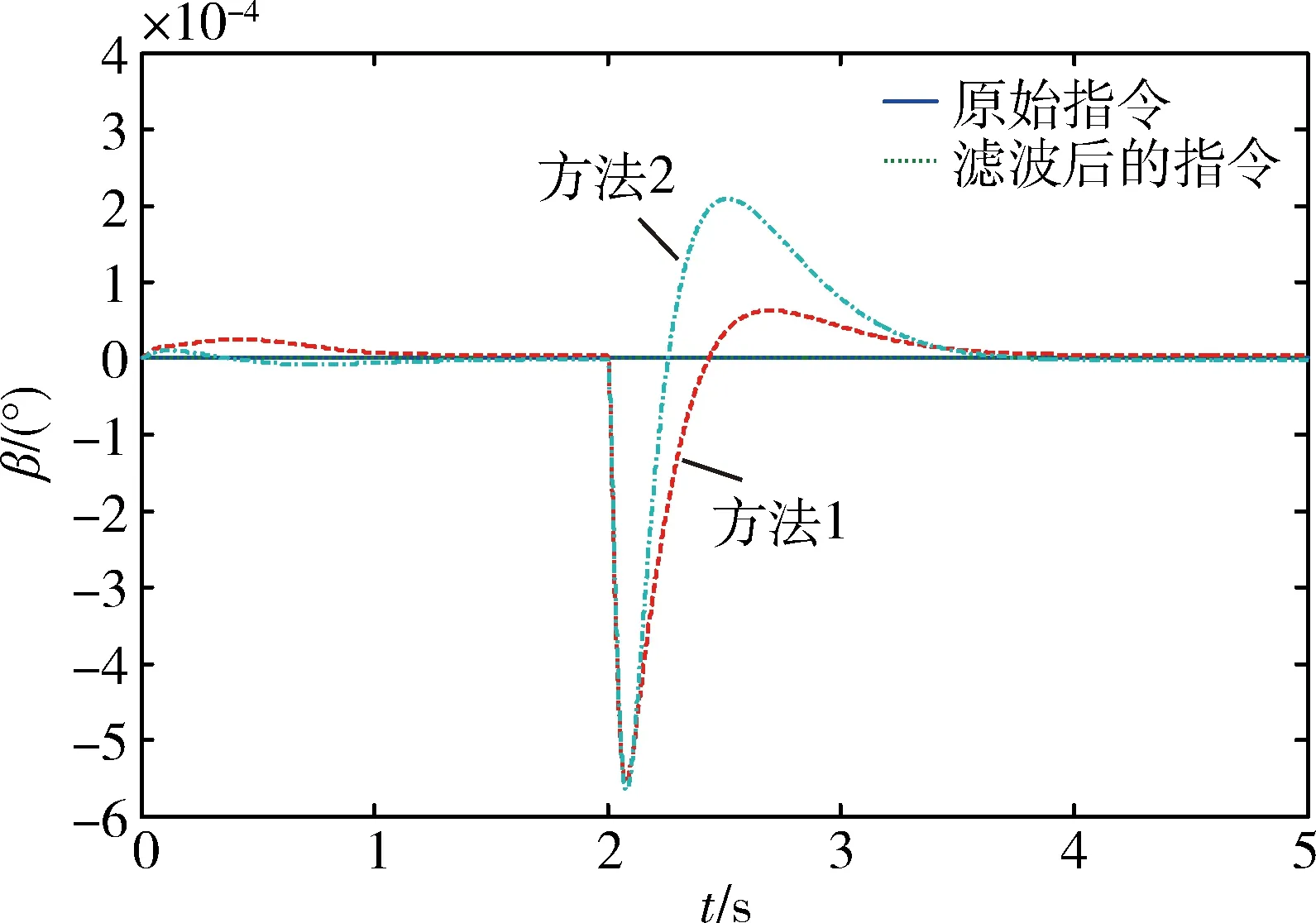
图3 侧滑角指令跟踪对比结果

由图2～10给出的仿真结果中，不难得出：

1)控制系统稳定性好，收敛速度快。对控制指令跟踪良好。当控制指令变化后，飞行控制系统仍能稳定跟踪指令信号，并迅速收敛到零附近；

图4 滚转角指令跟踪对比结果

图5 滚转角速度变化

图6 俯仰角速度变化

图7 偏航角速度变化

图8 副翼舵偏角变化

图9 升降舵舵偏角变化

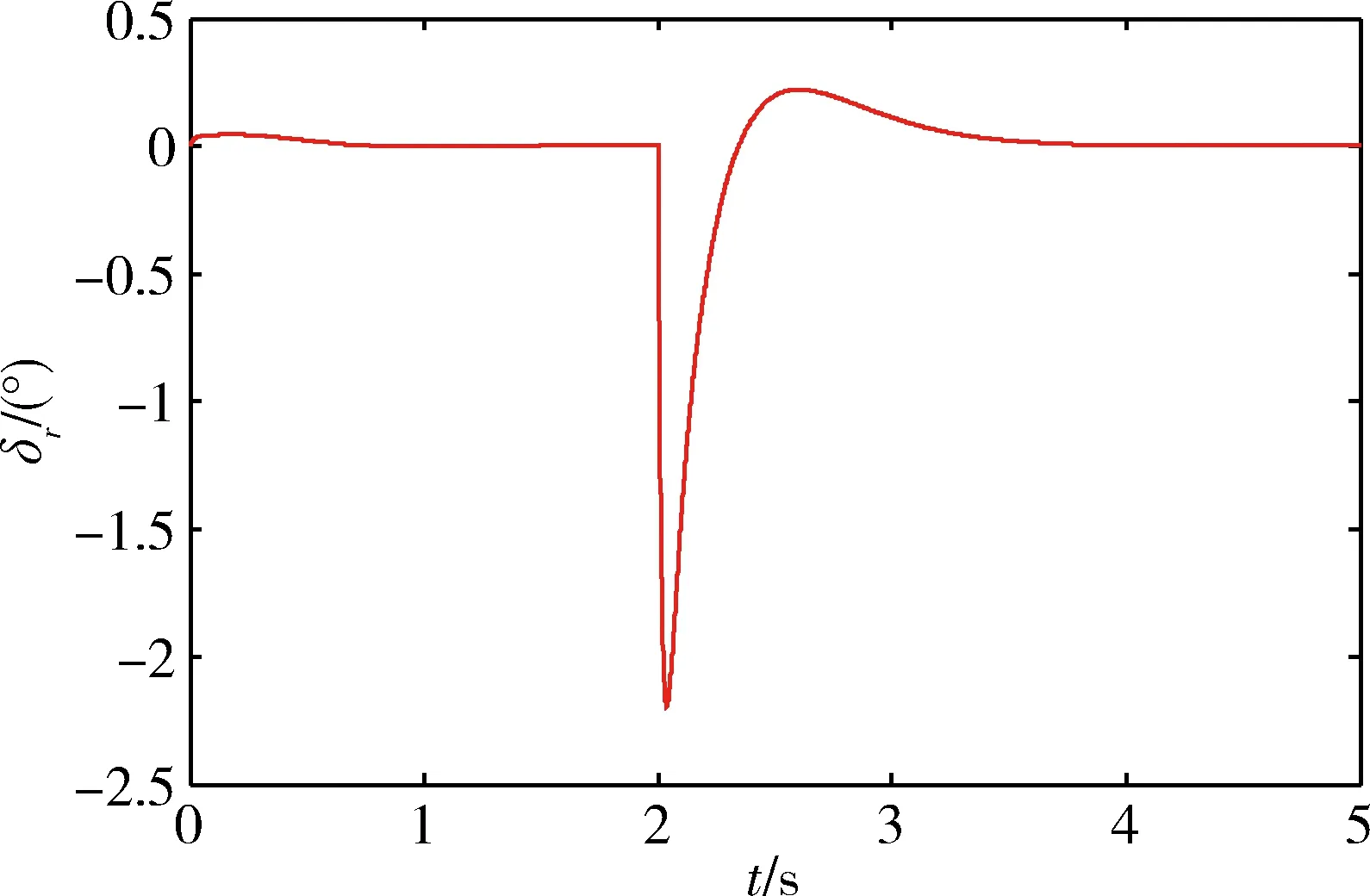
图10 方向舵舵偏角变化

2)在引入误差逼近器和未引入误差逼近器的对比仿真实验中，引入误差逼近器的方法能更好地跟踪指令，控制效果更好；

3)控制效能好，鲁棒性好，误差逼近器能够较好地完成对未知干扰的补偿。在整个飞行控制过程中，当控制指令变化后，控制舵面偏转角未出现饱和情况。虽然加入了气动参数和转动惯量的随机摄动，误差逼近器仍能消除干扰，未对控制器的稳定性和控制效果造成明显影响，表现出控制系统较强的鲁棒性。

5 结论

以反步法为基础，在引入误差逼近器的同时，结合动态面控制技术设计了一种误差逼近鲁棒非线性飞行控制器。首先，飞行器飞行过程中的外界干扰通过误差逼近器得到有效逼近；其次，引入动态面控制技术解决了利用反步法设计控制器时产生的“项数膨胀”问题；最后，通过仿真结果可知，在存在外界未知干扰的情况下，本文所设计的控制器具有很好的稳定性和鲁棒性，满足巡航飞行器的飞行控制要求。

[1] Lane S H, Stengel R F. Flight Control Design Using Nonlinear Inverse Dynamics[J]. Automatica, 1988, 24(4): 471-483.

[2] Kristic M, Kanellakopoulos, Kokotovic P. Nonlinear and Adaptive Control Design[M]. New York: John Wiley amp; Sons, 1995.

[3] Sharma M, Richards N D. Adaptive Integrated Guidance and Control for Missile Interceptors[R]. AIAA-2004-4880, 1995.

[4] Polycarpou M, Farrell J, Sharma M. On-line Approximation Control of Uncertion Nonlinear Systems: Issues with Control Input Saturation[R]. ADA436259-1995.

[5] Farrell J, Polycarpou M Sharma M. Adaptive Backstepping with Magnitude, Rate, and Bandwidth Constraints: Aircraft Longitude Control[R]. ADA442139- 2006.

[6] Sonneveldt L, Chu Q P, Mulder J A, et al.Constrained Adaptive Backstepping Flight Control: Application to a Nonlinear F-16/MATV Model[R]. AIAA-2006-6413, 2006.

[7] 朱铁夫，李明，邓建华.基于Backstepping控制理论的非线性飞控系统和超机动研究[J]. 航空学报，2005，26(4): 430-433.(Zhu Tiefu, Li Ming, Deng Jianhua.Nonlinear Flight Control System Based on Backstepping Theory and Supermaneuver[J]. Acta Aeronautica et Astronautica Sinica, 2005, 26(4): 430-433.)

[8] Harkegard O, Glad T. Vector Backstepping Design for Flight[J]. AIAA-2007-6421, 2007.

[9] Swaroop D, Hedrick J K, Yip P P, et al. Dynamic Surface Control for a Class of Nonlinear Systems[J]. IEEE Trans. on Automatic Control, 2000, 45(10): 1893-1899.

[10] Farrel J, Sharma M, Polycarpou M.Backstepping-based Flight Control with Adaptive Function Approximation[J]. Journal of Guidance, Control, and Dynamics, 2005, 28(6):1089-1102.

[11] 王坚浩，胡剑波，张博锋.应用非线性干扰观测器的反推终端滑模飞行控制[J]. 应用科学学报, 2012，30(4): 404-414.(Wang Jianhao, Hu Jianbo, Zhang Bofeng. Backstepping Terminal Sliding Mode for Flight Control Based on Non-linear Disturbance Observer[J]. Journal of Applied Sciences, 2012, 30( 4): 408-414.)

[12] Stevens B L, Lewis F L. Aircraft Control and Simulation [M]. 2nd ed.New York: John Wileyamp;Sons, 2003.

[13] 曹立佳，张胜修，李晓峰，等. 折叠翼飞行器发射段鲁棒非线性控制系统设计[J]. 航空学报，2011,32(10)：1879-1887.(Cao Lijia, Zhang Shengxiu, Li Xiaofeng, et al. Robust Nonlinear Control System Design for Folding-wing Aerial Vehicles During Launching Time[J]. Acta Aeroautica et Astronautica Sinica, 2011,32(10):1879-1887.)

[14] Keshmiri S, Mirmirani M D. Six-Dof Modeleling and Simulation of a Generic Hypersonic Vehicle for Conceptural Design Studies[R]. AIAA 2004-4805, Norfolk, Virginia: AIAA,2004.

[15] 钱杏芳，林瑞雄，赵亚男.导弹飞行力学[M].北京：北京理工大学出版社，2008.

[16] Swaroo D, Hedrick J K, Yip P P, et al . Dynamic Suface Control for a Class of Nonlinear Systems[J]. IEEE Transactions on Automatic Control, 2000, 45(10): 1893- 1899.

[17] Wang D, Huang J. Neural Network-Based Adaptive Dynamic Suface Control for a Class of Uncertain Nonlinear Systems in Strick-Feedback Form[J]. IEEE Transactions on Neural Networks, 2005, 16(1): 195-202.

[18] Tong S C, Li Y M. Observer-based Adaptive Fuzzy Backstepping Control of Uncertain Nonlinear Pure-feedback Systems[J]. Science China Information Sciences, 2014, 57: 1-14.

[19] Ploycrpou M M, Ioannou P A. A Robust Adaptive Nonlinear Control Design[J]. Automatica, 1996, 32: 423- 427.

BacksteppingControlforCruiseAircraftBasedonErrorEstimation

Yu Feixiong, Wang Yongchao, Cao Lijia, Zhang Shengxiu, Hu Xiaoxiang

Rocket Force University of Engineering, Xi’an 710025, China

Anerrorestimationrobustnonlinearcontrollerbasedonbacksteppingisdesignedforcruiseaircrafttofulfillthefairlygreatchangesofcharacteristicsandstronglynonlinearcontrolsystem.Firstly,a6-DOF (degree-of-freedom)nonlinearmodelisestablished.Byusingthelinearfeedbacktheory,thesystemisstrictlytransformedintofeedbackMIMOsystemswitherrors;secondly,thebacksteppingisusedtodesigncontrollawanderrorestimationlaw.Dynamicsurfacecontrolisemployedtoreplacethedifferentiationsofthevirtualcontrollawintraditionalbackstepping,whichisusedtohandletheproblemof‘termexplosion’.Finally,theclosed-loopsystemisguaranteedtobeboundedandtrackingerrorsarealsoprovedtoconvergeexponentiallytoasmallneighborhoodaroundzero.Thesimulationresultshowsthecontrollerhasstrongeffectivenessandrobustnessundertheunknownuncertaintyanddisturbance.

Errorestimation; MIMOsystems;Backsteepping;Dynamicsurfacecontrol;Cruiseaircraft

TP273.2

A

1006-3242(2017)04-0026-07

*国家自然科学基金资助(61304001,61304239)

2016-03-21

虞棐雄(1992-)，男，浙江缙云人，硕士，主要研究方向为飞行器鲁棒自适应控制；王永超(1991-)，男，河南周口人，博士研究生，主要研究方向为飞行器鲁棒自适应控制；曹立佳(1982-)，男，四川自贡人，博士，讲师，主要研究方向为飞行器控制、仿真与决策；张胜修(1963-)，男，河南驻马店人，博士生导师，教授，主要研究方向为组合导航与飞行器制导控制；扈晓翔(1982-)，男，山东寿光人，博士，讲师，主要研究方向为非线性系统鲁棒控制。