卫星姿控系统的鲁棒H2/H∞混合控制问题研究

刘善伍 张学钢 陈宏宇

上海微小卫星工程中心，上海 200050

卫星姿控系统的鲁棒H2/H∞混合控制问题研究

刘善伍 张学钢 陈宏宇

上海微小卫星工程中心，上海 200050

针对一类范数有界不确定性卫星姿态采样系统，研究了鲁棒H2/H∞控制问题，给出了卫星姿态控制系统鲁棒稳定的充要条件及相应的鲁棒H2/H∞保性能状态反馈控制律和最优鲁棒H2/H∞保性能状态反馈控制律，控制律的求取通过借助一类线性矩阵不等式(LMI)，或通过求取满足线性矩阵不等式约束的优化问题，避免了以往使用Lyapunov矩阵求解的保守性。仿真结果表明，系统在受到扰动后仍然是稳定的。

姿态控制；采样系统；鲁棒H2/H∞控制；线性矩阵不等式

卫星姿态控制器的设计往往是根据确定的数学模型进行，这就使得所设计的控制器无法适应未建模和外界扰动。针对这些问题，近些年来，很多学者将鲁棒控制理论逐渐应用到卫星姿态控制器的设计当中，并取得了很大进展[1-5]。但这些研究大多都是在连续域内进行，且仅限于单目标约束条件，并通过Lyapunov方法求解，因此所设计的控制可能无法应用到离散系统，且由于单目标控制忽略了系统其他方面的性能而使得所设计的控制器具有一定局限性。而通过Lyapunov方法求解具有较大的保守性。

对于以上问题，本文针对卫星模型的参数不确定性和未知的外界干扰力矩，建立了卫星姿态动力学和运动学模型，并将其进行了离散化，在离散域内通过LMI方法研究了混合H2/H∞目标鲁棒控制问题，给出了同时满足H2性能和H∞性能的鲁棒H2/H∞保性能控制器。而且在离散域内得到的控制器可以直接应用到实际的计算机离散控制系统中。

1 本文用到的几个主要引理

对于给定的时不变离散系统

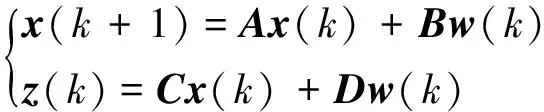
(1)

定义系统H2性能指标和H∞性能指标：

H2性能指标IE增益：

H∞性能指标EE增益：

引理1[6]：对于给定的常数γgt;0和系统(1)，以下条件是等价的。

1)系统(1)是渐近稳定的，且系统的EE增益Λeelt;γ；

2)存在一个对称矩阵Pgt;0，使得

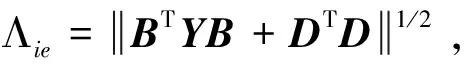
引理3[6]：给定适当维数的矩阵Y，D和E，其中Y是对称的，则

Y+DFE+ETFTDTlt;0

对所有满足FTF≤I的矩阵F成立，当且仅当存在一个常数εgt;0，使得

Y+εDDT+ε-1ETElt;0

2 问题描述

卫星的姿态动力学连续模型[7]为：

(2)

由文献[7]对卫星动力学模型进行推导转换得到连续域内状态空间模型：

(3)

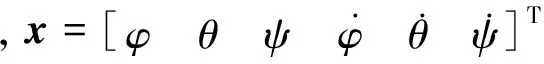
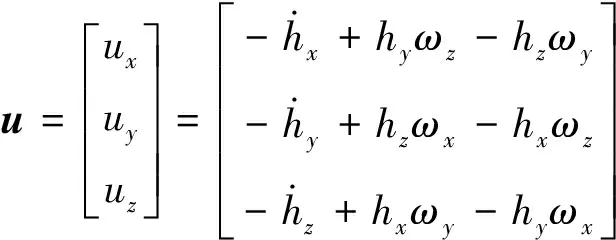
令系统矩阵扰动ΔA=UFV，其中U和V是已知矩阵，反映了不确定参数的结构信息，F∈Rn×n是不确定矩阵，且满足FTF≤I(Ι表示适当维数的单位矩阵)，则式(3)重写成：

(4)

对式(3)～(4)进行离散化得：

(5)

其中，G=exp[AT]，T为系统采样时间，

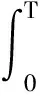
本节的目的是对给定的标量γgt;0，设计状态反馈控制律

u(k)=Kx(k)

(6)

使得对所有允许的参数不确定性和外部扰动输入闭环系统为

(7)

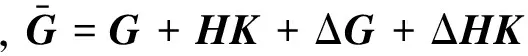
满足以下的设计指标：

1)闭环系统是渐近稳定的；

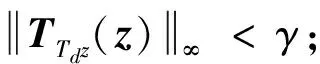
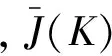
3 主要结果

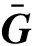
(8)

证明：由引理1和矩阵Schur补性质，定理1的第一部分很容易得到。

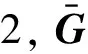
(9)

确定的矩阵。

式(8)减去式(9)得

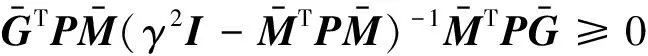
矩阵不等式(8)包含了参数不确定矩阵，要检验其对所有允许的不确定矩阵成立，必须将其转化为一个等价的线性矩阵不等式的可行性问题，从而可以应用LMI工具箱提供的线性矩阵不等式求解器来有效的检验定理1的条件。

定理2 存在一个对称正定矩阵P，使得条件不等式(8)对所有允许的参数不确定性成立，当且仅当存在常数εgt;0和对称正定矩阵Q，使得

(10)

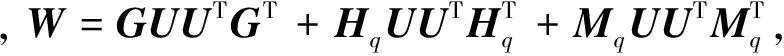
证明：由矩阵Schur补性质，矩阵不等式(8)成立等价于下式成立

(11)

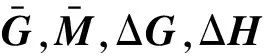
定理1和2证明了如果存在常数εgt;0，使得矩阵不等式(10)有正定对称解矩阵Q，则对所有允许的参数不确定性，闭环系统式(7)是渐近稳定的，且被调输出z(k)满足给定的扰动抑制约束。进而，这个正定解矩阵Q保证了性能指标J(K)满足

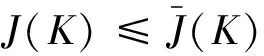
(12)

而这里

(13)

以下定理进一步给出了保证闭环系统渐近稳定，且满足给定的扰动衰减度和性能约束式(12)的保性能控制律设计方法。

定理3 对给定的常数γgt;0和闭环系统式(7)，存在一个保性能控制律式(6)，当且仅当存在常数εgt;0以及对称正定矩阵Q和矩阵Y，使得

(14)

进而，如果式(14)有一个可行解ε，Q，Y，则状态反馈控制律

u(k)=YQ-1x(k)

(15)

是系统式(5)的一个保性能控制律，且其闭环系统的一个H2保性能上界是式(13)。

证明：在式(10)中令Y=KQ，即可得到本定理。

定理3 提供了用线性矩阵不等式(13)的可行解表示的一组保性能控制律。特别地，基于这个参数化表示，提出鲁棒H2/H∞最优保性能控制律的设计方法。

定理4 对给定的常数γgt;0和系统式(5)，如果以下的优化问题

(16)

成立，则u(k)=YQ-1x(k)是系统式(5)的H2/H∞最优保性能控制律。

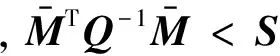
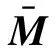
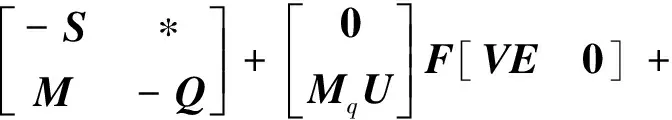
由引理3，上式对所有满足FTF≤I的不确定矩阵成立，当且仅当存在常数ε1gt;0，使得

上式经整理并再次应用引理1即可得到问题式(16)的条件式(2)。这样Trace(S)的最小化将保证性能上界J(K,Q-1)的最小化。约束条件和目标函数的凸性保证了如果问题式(16)有解，则一定是该问题的全局最优解，定理得证。

4 算例

某型号小卫星转动惯量为：Isx=1.31kg·m2，Isy=1.33kg·m2，Isz=1.1kg·m2。轨道角速度为：ω0=0.0011rad/s。仿真初始值设置为：三轴姿态角φ=5°，φ=-10°，ψ=-5°；ωx=-0.8(°)/s，ωy=1(°)/s，ωz=0.8(°)/s。扰动结构U,V取为：

此结构表征了卫星的转动惯量受到了干扰，干扰幅度约为标称值的20%。另外，取卫星外界干扰Td为零均值白噪声，取飞轮执行机构的控制力矩限幅为1mNm。给定γ=30，利用MATLAB中的LMI工具箱进行仿真，可得鲁棒H2/H∞最优保性能状态反馈控制器为

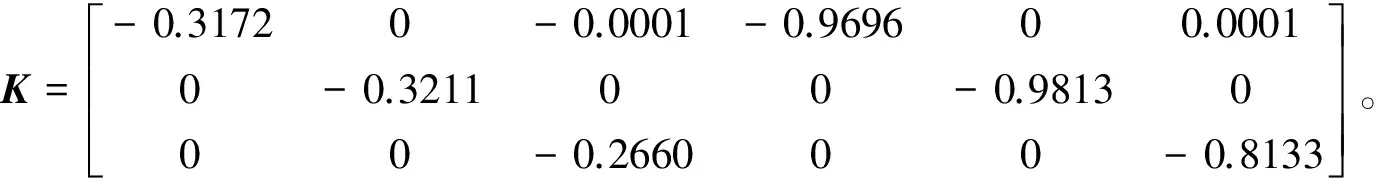
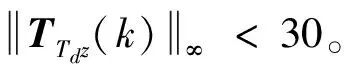
通过Matlab/Simulink搭建仿真模型，得到卫星姿控闭环系统受到扰动前后的姿态变化曲线如图1和2所示，从图中可以看到，受到扰动后，卫星三轴姿态仍然稳定，且超调量和调整时间变化不大。

图1 未受扰动卫星三轴姿态变化

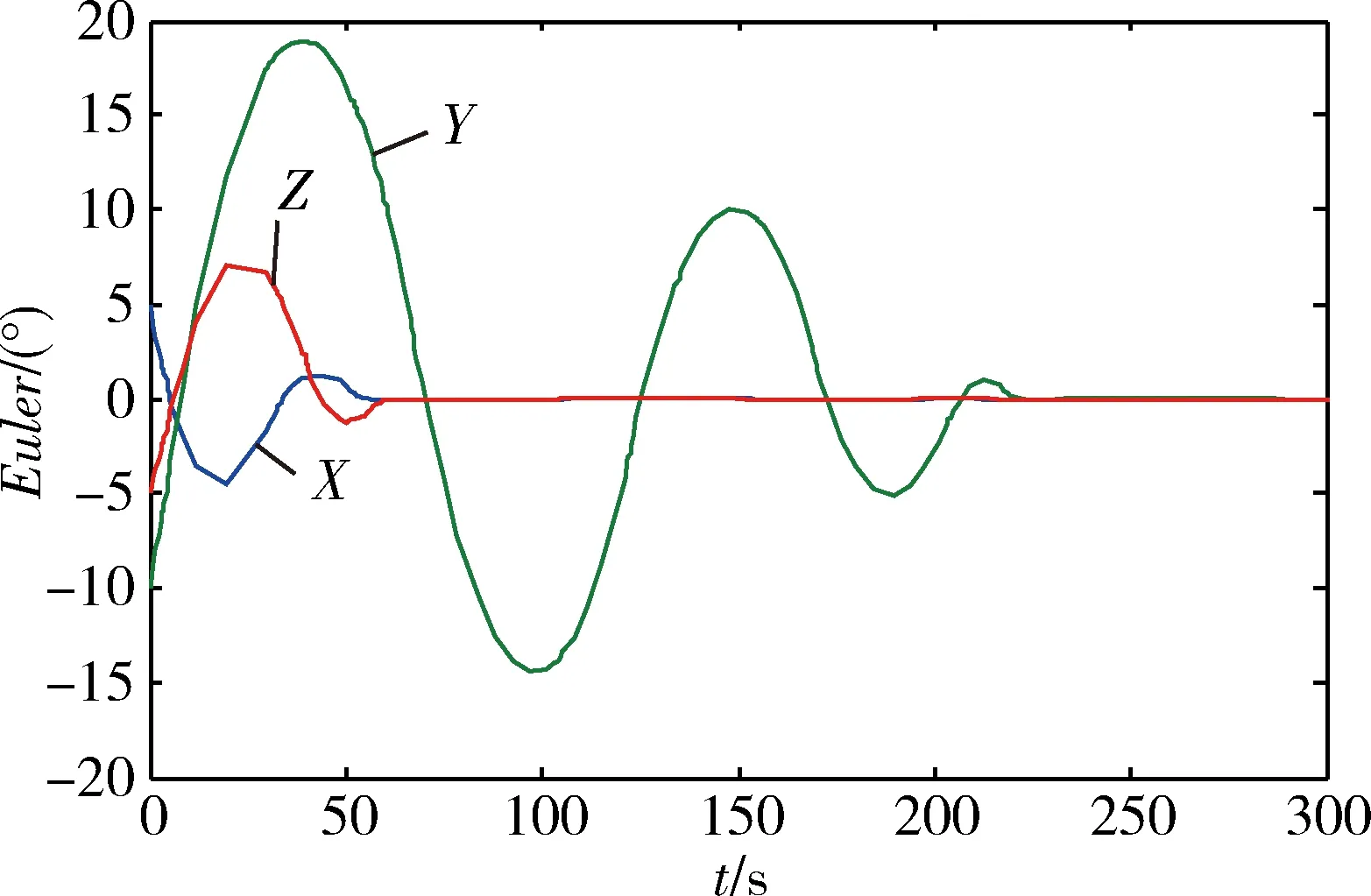
图2 受扰动卫星三轴姿态变化

5 结论

本文针对具有范数有界不确定性和外部扰动的卫星姿控采样系统设计了H2/H∞最优鲁棒保性能状态反馈控制器，仿真结果表明，在系统受到扰动的情况下，仍然是稳定的，且其动态性能变化不大，为未来的工程应用提供了强有力的理论基础。

[1] Sun Y P, Yang C D. MixedH2/H∞Attitude Control of a LEO Microsatellite in The Presence of Inertia Matrix Uncertainty [C]. American Control Conference, 2002. Proceedings of the 2002. IEEE, 2002, 2: 1354-1359.

[2] Liu C, Wang F, Shi K, et al. RobustH∞Control for Satellite Attitude Control System with Uncertainties and Additive Perturbation [J]. International Journal of Science, 2014, 1(2): 1-9.

[3] Cheng Y, Jiang B, Fu Y, et al. Robust Observer Based Reliable Control for Satellite Attitude Control Systems with Sensor Faults [J]. International Journal of Innovative Computing, Information and Control, 2011, 7(7): 4149-4160.

[4] Liu C, Wang F, Zhang Z. MixedH2/H∞Control for A Satellite Based on LMI [C]. Mechatronics and Control (ICMC), 2014 IEEE International Conference on. IEEE. 2014: 2114-2118.

[5] 刘善伍,张锐,张静.卫星姿态采样系统的鲁棒H∞控制[J],航天控制,2012,30(6):50-53. (Liu Shanwu, Zhang Rui, Zhang Jing. RobustH∞Control of a Class Sample-Data Systems for Satellite Attitude Control with Structured Uncertainty [J]. Aerospace Control, 2012, 30(6):50-53.)

[6] 俞立.鲁棒控制——线性矩阵不等式处理方法[M].北京：清华大学出版社,2002.

[7] 章仁为. 卫星轨道姿态动力学与控制[M]. 北京：北京航空航天大学出版社,1998.

TheH2/H∞RobustnessMixControlforSatelliteAttitudeControlSystem

Liu Shanwu, Zhang Xuegang, Chen Hongyu

ShangHai Microsatellite Engineering Center, Shanghai, 200050，China

Inthispaper,theH2/H∞robustnessmixcontrolforaclassofsampled-datasystemsisresearchedforsatelliteattitudecontrolwhoseunderlyingcontinuous-timesystemsaresubjectedtouncertainties,andprerequisitesofrobuststabilityandthecorrespondingrobustcontrollawarederived.Theacquisitionofcontrollawisdesignedbysolvingaclassoflinearmatrixinequalities(LMI)oradynamicoptimizationwithLMIconstraintsrespectively.ThemethodislessconservativethanLyapunovematrixmethod.Anexampleisshownthatsystemdisturbedisstable.

Sampled-datasystems；RobustH2/H∞control；Linearmatrixinequality(LMI)

V249.1

A

1006-3242(2017)04-0037-05

2017-02-20

刘善伍(1982-)，男，吉林农安人，硕士，主要研究方向为卫星控制系统设计，张学钢(1990-)，男，安徽蚌埠人，博士研究生，主要研究方向为卫星控制系统设计；陈宏宇(1976-)，男，大同人，博士，主要研究方向为卫星总体设计、控制系统设计。