基于GSA-BP神经网络的河流输沙量研究

张 凡

（山西省小浪底引黄工程建设管理局，山西 太原 030002）

基于GSA-BP神经网络的河流输沙量研究

张 凡

（山西省小浪底引黄工程建设管理局，山西 太原 030002）

根据《中国河流泥沙公报》数据资料，建立了以河流名称（编号）、时间、径流量为输入因子，河流输沙量为输出因子，拓扑结构为3-10-1的BP神经网络预测模型，并针对BP神经网络模型的不足，采用了万有引力搜索算法对BP神经网络的权值和阈值进行优化，并对该GSA-BP模型的模拟性能进行了分析。结果表明：所建立的GSA-BP河流输沙量预报模型模拟值与实测值的相关系数、平均相对误差分别为0.999和3.65%，并且两者之间无显著的统计学差异。该模型的模拟值与实测值之间具有较好的一致性和较高的模拟精度，可以用于河流输沙特性的定量预报。

万有引力算法；BP神经网络模型；径流量；河流输沙量

0 引言

河流的泥沙状况，不仅关系河流本身的发展演变，也反映了流域的环境特性、水土流失程度及人类活动的影响。在规划、防洪、水资源的利用和保护以及水土保持等方面的工作中，河流泥沙问题是必须考虑的重要因素。对我国相当多的河流来讲，治水必治沙，是中国水利的特点之一，也是难点之一[1]。许多学者围绕着黄河进行了大量的研究，例如黄河的输沙量变化趋势、人类活动对河流水沙变化的影响、水沙变化对地貌形成的影响、植被覆盖对水沙变化的影响等方面的研究，并取得了一定的研究成果。

河流输沙量的准确预报有着至关重要的作用和意义，前人采用的预报方法主要包括：水文法及水保法、支持向量机法、小波神经网络法[2]、BP神经网络法等。河流的输沙量年变化是一个复杂的非线性过程，可以将该变化过程看作为一个黑箱模型，通过构建BP神经网络模型，从而为河流泥沙的动态变化研究提供有效工具。但BP神经网络模型在使用过程中会存在搜索空间大，易陷入局部极值点等问题，限制了它在实际预测中的广泛应用。

万有引力算法（GSA）是基于牛顿万有引力定律的一种元启发式智能优化算法，在收敛性方面要优于粒子群算法和遗传算法等智能算法。该算法目前在无人机航路规划[3]、流水线调度[4]、边坡稳定分析[5]等方面得到了广泛应用，然而在河流输沙量预报方面的研究鲜有报道。通过构建基于万有引力算法优化后的BP神经网络模型，实现河流的输沙量准确预报，为河流的水沙管理提供支持。

1 BP神经网络模型原理

在1968年，以Rumelhart和McCelland为首的科学家小组首次提出了BP神经网络，它是目前模拟精度相对较高、应用范围最广的神经网络模型之一。通常BP神经网络由三部分构成：输入层、隐含层、输出层。误差反向传播算法的学习过程，由信息的正向传播和误差的反向传播两个过程组成。外界的输入信息首先由输入层接收，并传递给中间层神经元，然后经过中间层的信息处理后，最终传输给输出层，并由输出层向外界输出信息。当输出信息与期望不吻合时，便进入误差反向传播机制，各层间的权值矩阵和阈值矩阵进行不断调整，如此反复直至达到期望要求为止。

2 GSA算法流程

万有引力搜索算法GSA将所有粒子当作有质量的物体，在寻优过程中，所有粒子做无阻力运动。每个粒子都受到空间中其他粒子万有引力的影响，并产生加速度向质量更大的粒子运动。由于粒子的质量与粒子的适度值相关，适度值大的粒子其质量也会更大，因此，质量小的粒子在朝质量大趋近的过程中逐渐逼近最优解。GSA搜索算法的具体流程如下：

步骤1：初始化算法中的所有粒子的位置与加速度，并设置迭代次数与算法中的参数。

步骤2：对每个粒子计算该粒子的适应值，利用公式（1）更新重力常数。

其中，G（t）表示随引力变换的万有引力常数。G0表示在t0时刻G取值；T为最大迭代次数；t为时间；a为粒子的加速度。

步骤3：由计算得到的适应度利用式（2）和式（3）计算每个粒子的质量，

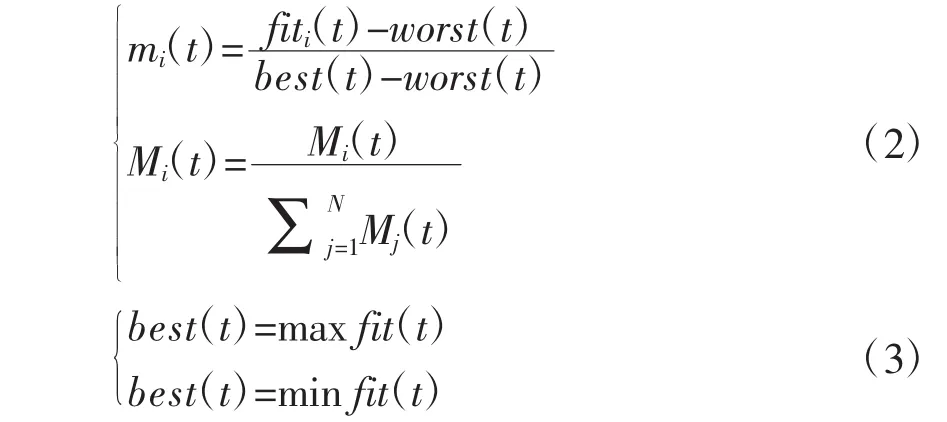
其中，fiti（t）表示粒子的适应值；best（t）表示t时刻中的最优解；worst（t）表示t时刻中的最差解；mi（t）规范化到[0，1]之间的粒子适应值。

步骤4：并利用公式（4）到公式（7）计算每个粒子的加速度。

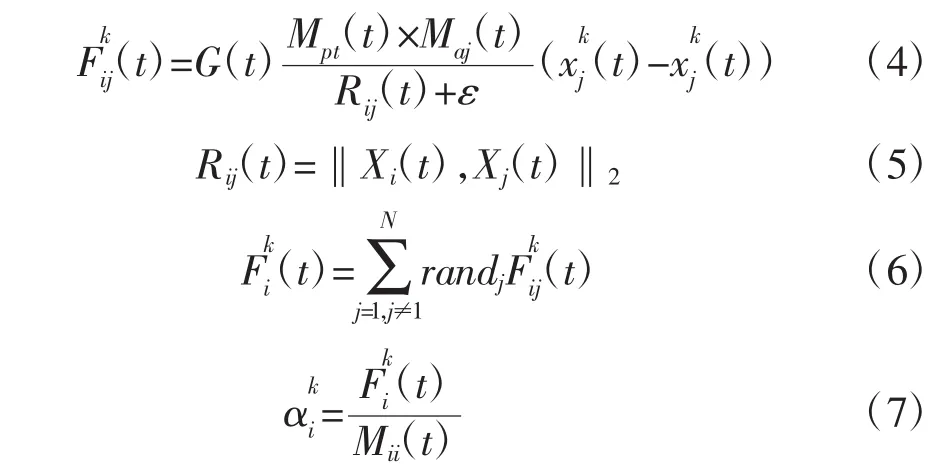
步骤5：根据式（8）计算每个粒子的速度，然后更新粒子的位置。

步骤6：如果未满足终止条件，返回步骤（2）；否则，输出此次算法的最优解。

3 GSA-BP神经网络模型的构建

3.1 训练样本和测试样本

本研究的数据主要来源于《中国河流泥沙公报》，经过整理得到2005—2013年长江、黄河、珠江、松花江4条河流的径流量与输沙量资料。本文将河流名称（编号）、时间、径流量3项作为输入项，将输沙量作为输出项，隐含层节点数通过试算法进行确定。资料总共有36组，其中28组作为训练组，其余8组作为预测组。

3.2 神经网络结构的确定

隐含层数目与模拟精度呈正比，但也可能会造成模型过于复杂等问题，通常选择单隐含层为宜。本文采用扩张法进行节点数的确定，通过多次试算，发现当节点数为10，经过73次训练后，模型的训练误差为7.1089E-5，能够达到了模型的训练精度要求。并且在多次试算中，该条件的节点数和训练次数均最小，因此认为10为合理的节点数。综上所述，本研究的模型拓扑结构为3-10-1。输入层传递函数为tansig函数，训练函数为trainlm函数，输出层传递函数则为purelin函数。优化算法采用共轭梯度法。训练目标误差为0.000 1。最大训练次数为1 000次。

4 结果分析

4.1 训练组模拟效果评价

图1 训练组实测值与预测值相关性图

图2 训练组样本相对误差

图1为训练组实测值与预测值间的相关关系图。由图1可以看出，实测值与预测值构成的线性拟合模型的拟合度达到0.999 0，方程的斜率为1.006 1，说明预测值与实测值之间具有较强的线性相关性，并且预测值与实测值之间能够保持较好的一致性。图2为训练组各个样本的相对误差。由图2可知，实测值与预测值之间的最大相对误差为13.15%，最小误差为0%，平均相对误差为3.06%，模型的平均相对误差较小。此外，本文采用统计学方法对实测值与预测值之间的差异性进行了统计学分析，结果如表1所示。由表1可以看出，t值的绝对值小于t检验临界值，即＜t0.0（527）＝2.052，实测值与预测值间的差异并未达到显著水平。综上所述，该BP神经网络模型具有较好的一致性和较高的模拟精度，达到训练要求，可以用来进行输沙量的模拟预报。

表1 实测值与预测值t配对检验结果（训练组）

4.2 预测组模拟效果评价

图4 预测组实测值与预测值相关性图

图5 预测组样本相对误差

图3为预测组的实测值与预测值间的相关关系图。由图3可以看出，实测值与预测值构成的线性拟合模型的拟合度达到0.998 7，方程的斜率为0.997 5，说明预测值与实测值之间具有较强的线性相关性，并且预测值与实测值之间能够保持较好的一致性。图4为训练组各个样本的相对误差。由图4可知，实测值与预测值之间的最大相对误差为12.81%，最小误差为1.19%，平均相对误差为3.65%，模型的平均相对误差较小。表2为预测组样本的实测值与模拟值间的统计学差异性分析结果。经计算，实测值与预测值之间并无显著的统计学差异。综上所述，该BP神经网络模型的预测效果较好，能够胜任河流的输沙量预报模拟工作。

表2 实测值与预测值t配对检验结果（预测组）

5 结论

本文将万有引力搜索算法与BP神经网络结合用于建立河流输沙量预报模型，把求解BP神经网络各层权值、阀值的过程转化为万有引力搜索最优解的过程。以2005—2013年长江、黄河、珠江、松花江4条河流的径流量与输沙量资料作为研究样本，提出了GSABP算法，构建了河流输沙量预报模型。该算法融合了万有引力搜索算法的全局寻优能力和神经网络的泛化能力。经计算，该模型的训练组与模拟组的预报相对误差分别为3.06%和3.65%，模拟值与实测值之间具有较好的一致性和较高的模拟精度，可以实现河流输沙量的准确预报。本研究构建了河流输沙量的定量预报模型，在具体应用时，只用输入河流代码编号、预测时间、径流量，便能准确预报该条件下的河流年输沙量。多种预测模型的相互结合，以及模拟算法的改进，也是进一步的研究方向。

［1］吴华林，沈焕庭，朱建荣.河口泥沙通量研究综述［J］.泥沙研究，2001（5）:73-79.

［2］彭荔红，方志山，李祚泳.流域输沙量和输沙率的B-P人工神经网络预测［J］.水土保持学报，2001，15（S1）:22-25

［3］李沛，段海滨.基于改进万有引力搜索算法的无人机航路规划［J］.中国科学:技术科学，2012，10:1130-1136.

［4］谷文祥，李向涛，朱磊，周俊萍,胡艳梅.求解流水线调度问题的万有引力搜索算法［J］.智能系统学报，2010，05:411-418.

［5］蒋建国，谭雅，董立明，汪翠.改进的万有引力搜索算法在边坡稳定分析中的应用［J］.岩土工程学报，2016，03:419-425.

TV143+.4

C

1004-7042（2017）10-0006-03

张凡（1991-），男，2012年毕业于太原理工大学农业水利工程专业，助理工程师。

2017-08-11；

2017-09-19