一种数字高精度秒脉冲生成方法

赵 海，吕超英，梅 平

（无锡华润矽科微电子有限公司，江苏无锡 214135）

一种数字高精度秒脉冲生成方法

赵 海，吕超英，梅 平

（无锡华润矽科微电子有限公司，江苏无锡 214135）

提出了一种高精度的秒脉冲生成方法，依据晶体的温度特性，采用分段拟合的方法估算晶振误差。在不同工作温度下对振荡频率进行时间补偿，产生高精度秒脉冲信号。该方法可应用于低功耗SoC的实时时钟设计中。

秒脉冲；分段拟合；时间补偿；实时时钟

1 引言

基于可穿戴SoC（System on Chip，系统级芯片）的RTC（Real-Time Clock，实时时钟）需要满足在宽温范围内进行准确计时的要求。准确计时取决于几个重要参数，包括初始精度（指器件在常规条件下最初使用的精度）和温度系数（估算温度变化造成的误差）。

其中，初始精度主要受晶振质量的影响，精度越高价格也越贵，通常比较经济的方法是根据具体情况对晶振的初始频率进行简单的补偿。由于晶体频率随环境温度发生变化，要使RTC在不同温度下都能保持较高的精度，最有效的办法是对时间进行补偿，而时间的补偿其本质为晶振的频率补偿。

现有技术主要分为模拟补偿和数字补偿两种。其中模拟温度补偿通过改变石英晶体振荡器两端并联接地的负载电容大小，来改变晶振谐振频率[1]。数字温度补偿通过实时时钟芯片、外部MCU、温度传感器组成一个温度误差补偿网络，通过配置时钟芯片内部数字调整寄存器来实现晶振的频率补偿[2]。这些方法需要大量的缓存，而且占用CPU。本文提出的修正方法是一种纯硬件结构，工作过程中无需CPU干预，且不需要占用大量的缓存空间，具有相对精度高、功耗低和成本低的特点。

2 基本原理

2.1 晶振误差与温度的关系

石英晶体特性随环境温度的变化而变化，一般来说，晶振误差与环境温度的关系[3]如图1所示，基本上可以用一个二次曲线来表示，即与常温情况相比，环境温度升高和降低都会引起晶振频率变慢。

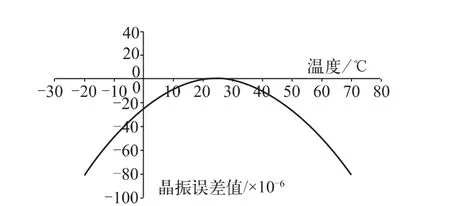
图1 晶振误差曲线图

一般的石英晶体可以用二次曲线拟合，很多厂商筛选整体都是根据二次曲线的二次方系数来进行晶振筛选，选择一致性较好的晶振。二次曲线函数如式（1）所示，其中y是温度转变时的偏差，单位是×10-6，x是环境温度。

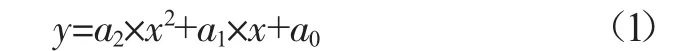
表1记录了某晶振在不同温度下的精度误差，后面的分析先以这组参数为基础进行。

表1 精度误差实测表

采用matlab二次曲线拟合函数polyfit(x,y,2)求得晶体误差式（1）的相关系数，其中a2=-0.0347，a1=1.6969,a0=-20.9772，由此可见，二次曲线的中心温度为24.4℃。

图2为该晶体二次曲线拟合图，横轴表示温度（单位摄氏度），纵轴表示晶体误差（×10-6）。

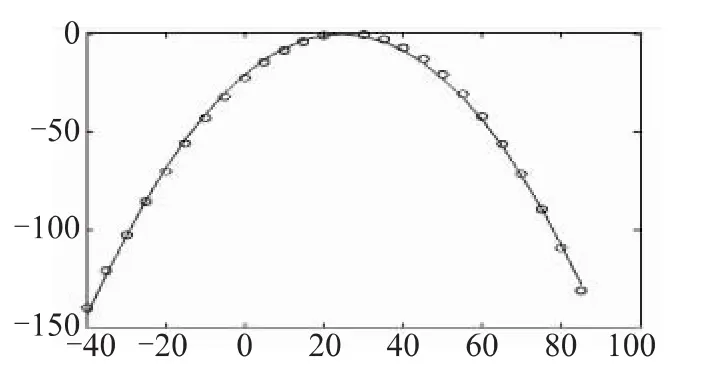
图2 晶振误差Matlab拟合图

2.2 补偿原理

根据文献[4]，晶振误差可以用式（2）表示，其中f为实际的振荡频率，f0为标准频率(即32768 Hz)：

也可以描述为1 s用频率为f0的晶振需要振动32768个周期，用频率为f的晶振需要振动32768+comp_value个周期，所以可以得到式（3）：

可以用式（4）得到的值，补偿当前工作的晶振f中得到标准的工作频率f0。由于一般晶振误差的绝对值不会超过500×10-6，所以comp_value的值不会超过16.384个脉冲，所以每秒钟补偿的脉冲个数不会超过17个。如果希望任何时候测量的时间都准确，那么每1/2秒的脉冲补偿个数不会超过9个，每1/4秒的脉冲补偿个数不会超过5个，每1/8秒的脉冲补偿个数不会超过3个，每1/16秒的脉冲补偿个数不会超过2个，每1/32秒的脉冲补偿个数小于1个。

3 实现方法

高精度秒脉冲生成流程框图如图3所示，采用12 bit ADC温度检测模块获取当前晶振的工作环境温度，根据当前温度求得精度误差，根据精度误差求得补偿值，最后生成秒脉冲。

图3 高精度秒脉冲生成设计流程

3.1 精度误差计算模块

实际应用中很多晶体并不是简单的二次曲线，特别是在温度较低和温度较高的地方差别更大。所以这个模块设计的时候将拟合曲线分成了三段，如式（5）所示。

当一个二次曲线就可以拟合得很好时，三段二次曲线可以用同一个表达式表示，即la2=ma2=ra2，la1=ma1=ra1，la0=ma0=ra0。当出现低温部分拟合曲线与常温部分拟合曲线偏差较大时，la2、la1、la0就可以描述低温部分的曲线。同理，当高温部分拟合曲线与常温部分拟合曲线差异较大时，ra2、ra1、ra0就可以描述高温部分的曲线。其中x＜low_temp表示低温部分，x＞high_temp表示高温部分。可以参考图4。图4中的二次曲线可以分为3段，左边的一段对应图中left标记处，表示温度较低时的拟合曲线，中间的一段对应图中middle标记处，表示常温时的拟合曲线，右边一段对应图中right标记处，表示温度较高时的拟合曲线。

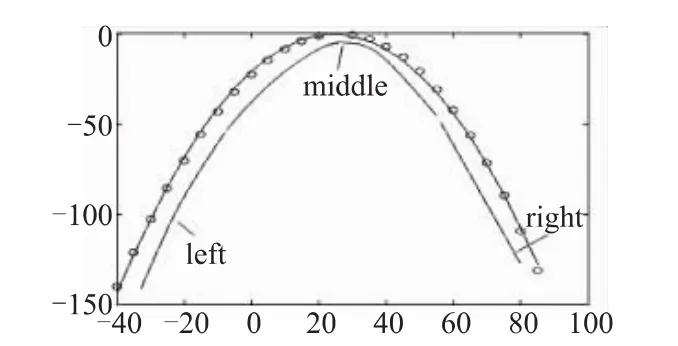
图4 三段式拟合曲线图

3.2 补偿值计算模块

将晶振误差CrystalError值代入补偿值式（4）中，该公式中的f0为标准震荡频率，其值是32768 Hz，从而由补偿值计算电路计算出每秒钟补偿的脉冲个数，即秒脉冲补偿个数。由于硬件除法器耗费面积大，因此采用式（6）的等价表达方法代替32768/1000000，选定 n=28，x=8796093=0x8637bd。

由于晶振误差不会超过500×10-6，所以用32768/1000000计算出来的补偿值是16.384，用8796093/（2的28次方）计算出来的补偿值也是16.384。

3.3 秒脉冲生成模块

用标准32768 Hz的时钟源，1 s需要32768个时钟周期。当温度变化导致晶体输出的时钟源不是标准的32768 Hz时，由2.2节介绍知道这个时候1 s需要32768补偿n(n为补偿值)个时钟周期。知道每1/32秒的脉冲补偿个数小于1个。每计数到1024时，将final_comp_value值的小数部分与1/32秒对应的脉冲补偿个数相加，如果final_comp_value的整数部分大于等于1，那么时钟计数器就停一拍不加或者加2，然后将final_comp_value的整数部分清零，将final_comp_value的小数部分继续保留，留给后面进行误差累加。实现框图见图5。

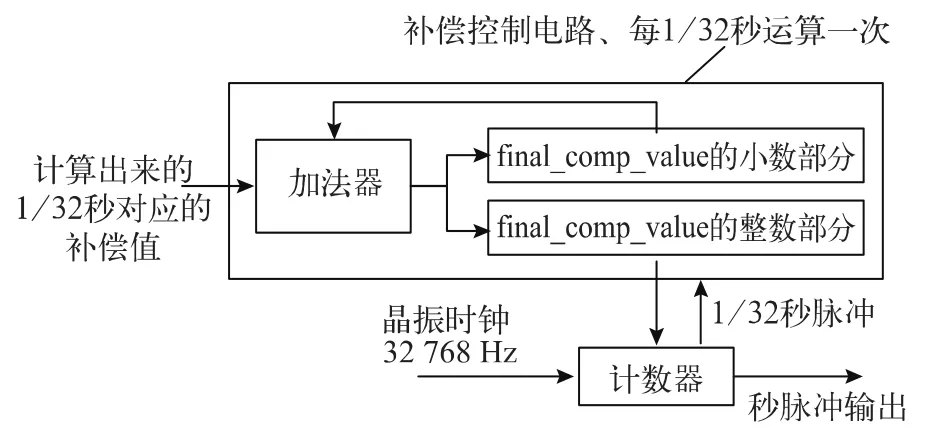
图5 秒脉冲生成框图

4 仿真结果

本文采用三段式二次曲线晶振误差拟合的方法，采用Verilog HDL硬件设计语言完成RTL设计。仿真波形图如图6所示，clk表示原始晶体，频率在32768Hz附近，频率会随温度产生偏移。temp_in表示的是当前ADC测试到的温度值，temp_in的数值为实际温度的16倍，温度值更新周期最小为1 s，只有在温度发生变化时，才重新计算补偿值。error_out为精度误差计算模块的输出，ppm_out为补偿值计算模块的输出。rtc_1hz为补偿后的1 s时间。

图6 秒脉冲生成仿真

5 结论

本文采用三段式二次曲线晶振误差拟合的方法，原始晶体的频率在32768 Hz附近，频率会随温度产生偏移。随着周围环境的温度变化，用来检测温度的ADC测量的温度值也会发生变化，该电路会重新计算补偿值，修正补偿误差，产生精准的秒脉冲。

本文的精度误差控制在1/32768，也就是30.517578125×10-6，如果进一步采用四舍五入法，误差精度再缩小一半，也就是15.2587890625×10-6。如果不考虑曲线拟合误差和温度切换过程中引入的误差，并假设final_comp_value在实际运算中可以保留小数点后无穷位长，长期累加后不存在累计误差，误差值一直保持在 15.2587890625×10-6。

[1]Huang Qiuting,Basedau P.Design considerations for highfrequency crystal oscillators digital trimmable to sub-ppm accuracy[C].IEEE,transactions on VLSI systems.

[2]梁世清，包海泉，季海涛，等.内置RTC作为电能表计时时钟的应用[J].自动化仪表，2013,33（1）：76-78.

[3]王永红，徐炜，郝立平.STM32系列ARM Cortex-M3微控制器原理与实践[M].北京：北京航空航天大学出版社，2008.

[4]吴培才，刘进忙，胡国平.温度补偿晶体振荡器[M].北京：国防工业出版社，1994.

赵 海（1974—），男，江苏江阴人，高级工程师，1997年毕业于浙江大学电子工程专业，无锡华润矽科微电子有限公司研发总监，多年来一直专注于集成电路的设计与开发，其负责和参与的项目先后两次获得江苏省科技进步奖。

A Digital High Precision Pulses Generation Method

ZHAO Hai,LV Chaoying,MEI Ping
（Wuxi China Resources Semico Co.,Ltd,Wuxi 214135,China）

The paper presents a high precision pulses generation method.Based on the temperature characteristics of crystal oscillator,a piecewise fitting method is used to estimate the vibration error,the frequency of oscillations is compensated at different working temperatures,generates high precision pulses per secondsignalafter compensation.Itcanbe usedinRTCdesignoflow power SoC.

pulsesper second;piecewise fitting;time compensation;RTC

TN402

A

1681-1070（2017）11-0023-03

2017-06-27