基于Flow-3D的抗拖网海床基冲刷数值模拟

于凯本，杨 涛，高 健，林广义，孟庆健，宗 乐

(1.国家深海基地管理中心，山东 青岛 266200；2.青岛科技大学 机电工程学院，山东 青岛 266100)

基于Flow-3D的抗拖网海床基冲刷数值模拟

于凯本1，杨 涛2，高 健2，林广义2，孟庆健1，宗 乐1

(1.国家深海基地管理中心，山东 青岛 266200；2.青岛科技大学 机电工程学院，山东 青岛 266100)

基于Flow-3D软件,建立抗拖网海床基沙土基床冲刷的三维数学模型，控制水流流速和泥沙粒径，对不同条件下抗拖网海床基周围沙土基床的冲刷进行数值模拟,并分析了抗拖网海床基最大冲刷深度随这两种因素改变的趋势。结果表明，抗拖网海床基沙土基床冲刷坑深度随海流流速增大而增加，在设定其他条件不改变的情况下，冲刷坑的加深速度随着流速增大会逐渐减缓，最终达到冲淤平衡。同时，由于海底环境复杂多变，导致模型与实际情况有一定的差异，还需在后续的研究中进一步进行优化。

抗拖网海床基；泥沙冲刷；数值模拟

0 引言

海床基作为一种坐底式海洋监测装置，一般布放于海洋沿岸、近海潜岸以及河口等区域，对悬浮泥沙参数、流速剖面、水温、潮汐及波浪等水流动力学参数进行长期、连续跟踪监测。由于布放区域是污染物、泥沙以及水流最大的区域，作为坐底长期环境监测设备在大浓度泥沙水域极易被泥沙覆盖，高的水流速度易使海床基平台底部海底沉积物被掏空导致平台倾斜倒塌。海床基的覆盖和倒塌会降低海床基的回收效率，降低了海床基搭载设备的安全性和可靠性，增加海床基的应用制造成本，导致不必要的经济损失[1]。因此，海床基坐底状态下周围沙土基床冲刷机理的研究对于提高海床基的回收安全性及对海床基外形优化具有重要作用。

本文运用美国Flow science公司开发的计算流体动力学(CFD)软件Flow-3D中FAVOR技巧以及有关自由液面的VOF方法对海床基处于不同流速和不同泥沙粒径的冲刷机理进行了仿真模拟。以期为海床基的布放及整体结构优化提供一定的参考。

1 控制方程

针对本文拟计算算例，所建立的数值水池需模拟三维海床面上抗拖网海床基周围泥沙在单向海流作用下的冲刷情况，即海流绕过抗拖网海床基与海床之间的相互作用。本文采用RNGk-ε模型进行求解。RNGk-ε模型对湍动粘度进行修正，考虑了平均流动中的旋转及旋流流动情况，可以更好地处理高应变率及流线弯曲程度较大的流动。

RNGk-ε模型具体表示如下[2]：

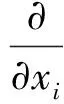
(1)

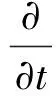
(2)

式中：xi为i方向坐标，t为时间(s)，ρ和u分别代表流体的密度(kg/m3)和速度(m/s)，gi为重力加速度(m/s2)。其中雷诺平均应力定义为：

(3)

RNGk-ε湍流模型中的k方程和ε方程分别表示为：

(4)

(5)

其中：

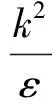
2 冲刷沉积模型

Flow-3D可以通过泥沙冲刷模块对流体中泥沙运动状况进行分析。泥沙冲刷模块是通过模拟在水流作用下的泥沙运动来预测泥沙侵蚀、平流扩散和沉积。该模块的主要应用有：(1)计算悬移质泥沙在平流水流中的扩散输移问题；(2)计算由于重力作用而产生的泥沙沉降问题；(3)计算由于剪切和水流扰动而挟带的泥沙问题；(4)计算由于泥沙颗粒随着河床滚动或者跳动而引起的推移质泥沙输移问题。

该模型的建立部分假定泥沙颗粒为球形并且他们的速度要小(从而使各个泥沙颗粒周围的流体以粘性效应占主导地位)。沉淀(漂移)系数Df通过式(6)自动计算：

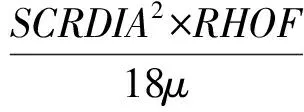
(6)

式中：SCRDIA是平均粒径，RHOF是流体密度。冲刷的“起动”组件是一个经验模型，该模型是以推移质输沙模型为基础。在填充层的界面计算出的“起动”速度是：

(7)

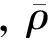
τc=SCRCRT×SCRDIA×g×(SCRRHO-RHOF)

(8)

式中：g为重力加速度；SCRRHO代表沉淀颗粒的密度，泥沙的典型密度值是2.65 g/cm3。

当沉积物含量大于等于沉积物临界含量 (SCRFCR)，沉积物即被认为已经堆积，堆积密度等于SCRFCR×SCRRHO。因此，在含沙量(CGS，单位为g/cm3)等于或大于SCRFCR×SCRRHO的地方有沉积物淤积，流体不会发生流动，施加在液体上的拖曳力被假定为无穷大(逆液拖曳数量，由Flow-3D计算的阻力系数为零)。在沉积物的体积分数大于沉积物聚集含量(SCRFCO)，但小于SCRFCR的区域，拖动模型被激活；沉积物拖动(SCRDRG)在这个模型中，相当于TSDRG(默认值是1.0)。当沉积物的体积分数小于SCRFCO，拖动模型没有被激活，但根据式(9)粘度会增强：

(9)

式中：μ0是流体的粘度，μ是由于沉积物的存在引起的粘度增强。

3 抗拖网海床基沙土基床冲刷模型

3.1 冲刷模型

本文对单向流作用下抗拖网海床基沙土基床冲刷进行数值模拟分析，在Flow-3D软件中建立与物理试验模型相同的三维数值模型进行模拟，通过对模拟结果分析，以验证冲刷模型条件参数及边界条件的可靠性。

抗拖网海床基模型圆台形底面直径φ=1.8 m，整体高度h=0.628 m。

泥沙颗粒粒径是仿真模拟的重要组成部分，粒径的选取对模拟结果的准确性有较大的影响。许炯心 等[3]利用1999年汛前深层钻孔取样资料和历年淤积实测大断面资料分析得到1960年前下游河道主槽淤积物中粒径大于0.1 mm的泥沙占50.7%，这种泥沙在下游淤积比高达83.1%。所以在本次模拟中泥沙粒径选取0.14 mm，泥沙休止角为31°，临界希尔兹参数为0.05。数值水槽的长度为20 m，宽度为6 m，高度为4 m。模拟中以矩形模拟水域的下表面为基准面，在此基准面的基础上建立高度为1 m的泥沙仿真区域。由于速度边界提供的是沿整个水深均匀的流速，这样就会在底部海床面泥沙范围内加入流速，不符合实际情况，且流速的存在可能会将入口附近的海床面泥沙带走，为防止此情况发生，在左右边界加入与海床面泥沙高度相同的实心挡板[4](图1中模型的蓝色和红色部分)。

图1 抗拖网海床基沙土基床冲刷模型Fig.1 Scouring model of Trawl Resistant Seabed Basement on sand bed

3.2 网格划分

利用CFD软件中的网格划分功能对抗拖网海床基沙土基床冲刷模型网格进行了划分，网格总数为100×60×50，形状为均匀六面体网格。由于模型主要模拟抗拖网海床基周围的流场变化和泥沙冲刷的地形变化，所以为了使模拟时计算能够更精确，对抗拖网海床基周围网格进行了加密处理，如图2和图3所示。

图2 模型网格划分平面图Fig.2 Model meshing ichnography

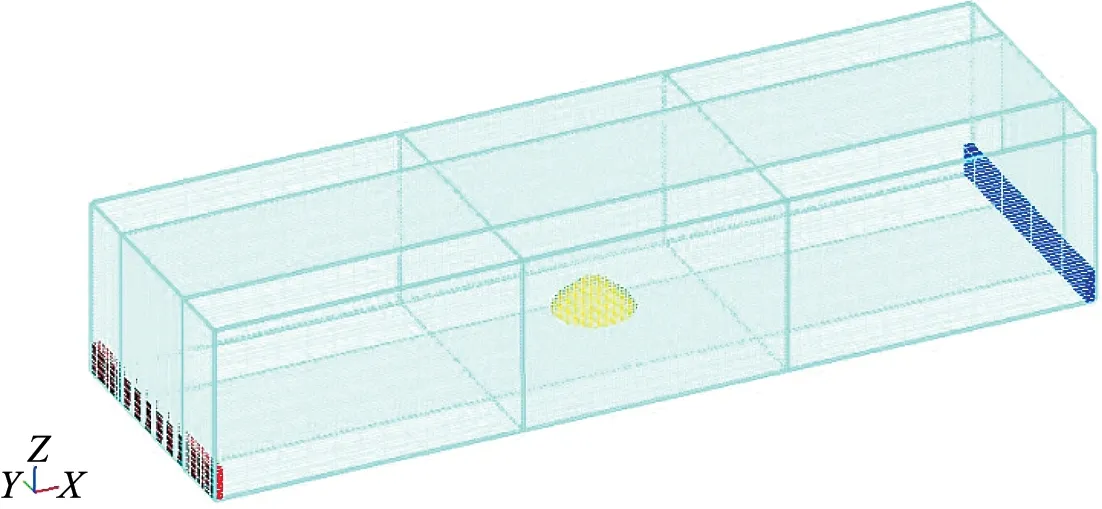
图3 模型网格划分立体图Fig.3 Model meshing stereogram

4 求解策略及模拟边界条件设置

本文采用广义的GMRES算法，该方法的残差极小，且收敛速度快，计算精度高，求解时不易产生发散，在求解N-S方程时与其他压力速度的分离式解法相比有很高的效率。

在冲刷模拟中需要考虑重力对结果的影响，因此本文设定重力矢量的大小为9.81 m/s。本文创建了两相流(水和泥沙)模型，最底层为泥沙，高度为1 m；泥沙层上面的区域全部设置为海水。

由于海水流速受季节、潮汐及深度等多方面的影响，参照文献[5]，对海水的模拟速度进行选择。

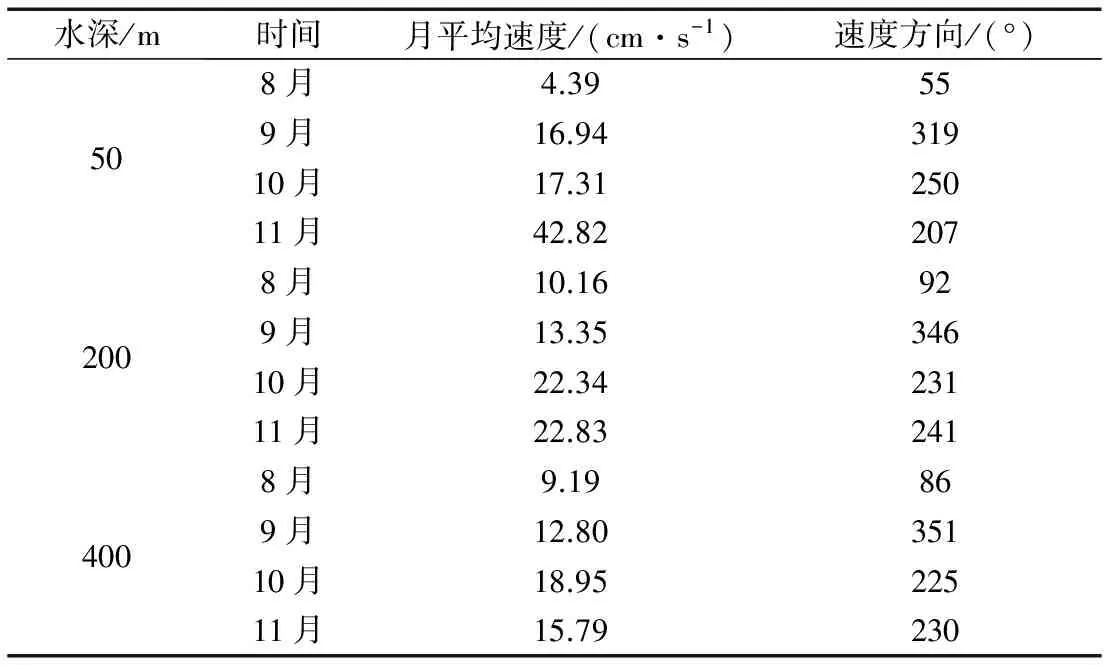
表1 2000年南海东北部8—11月每月平均流速与方向[5]Tab.1 Monthly mean velocity and direction in the northeastern part of the South China Sea in Aug.-Nov.,2000[5]

由表1可知，海水的速度随着深度的增加而逐渐减小，并且因季节的不同而有所差异，为了模拟结果具有代表性，在海流速度的取值中取较大值。所以，进流侧设置恒定流速0.40 m/s，边界条件的类型设置为Specified velocity。出口边界：边界条件的类型设置为Outflow。前后边界和上下边界：前后边界采用默认镜像无通量边界，其类型设置为Symmetry；下部边界的类型设置为Wall。具体边界类型如图4所示。

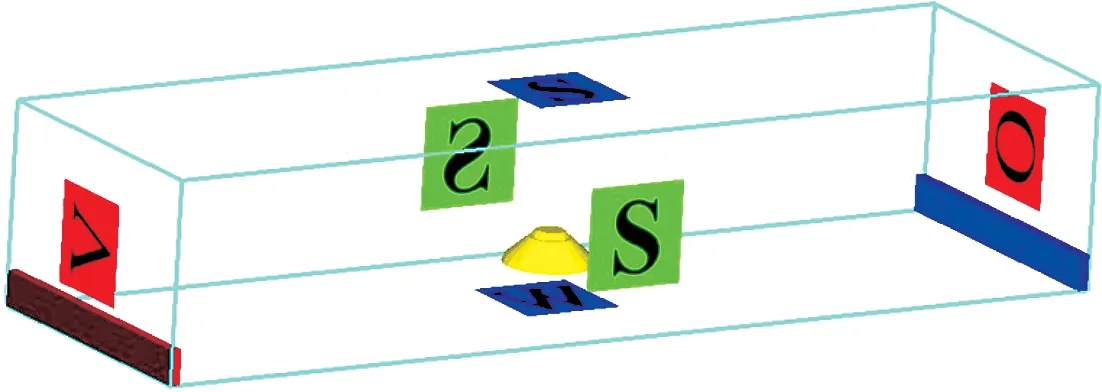
图4 模型边界条件设置Fig.4 Setting model boundary conditions

5 冲刷的数值模拟与分析

5.1 冲刷机理的数值模拟

流速为0.40 m/s，泥沙粒径为0.14 mm的条件下，抗拖网海床基沙土基床冲刷过程中不同时间下的冲刷坑深度值如表2所示。数值模拟过程中冲刷坑形成的速度比实际冲刷中冲刷坑形成的速度慢。当冲刷开始时，由于受到抗拖网海床基周围水流和漩涡的作用，抗拖网海床基下面的泥沙被水流冲刷挟带，在抗拖网海床基前端逐渐形成很小的冲刷坑，此过程中冲刷坑形成迅速，变化比较明显。随着冲刷的继续进行，抗拖网海床基冲刷坑的前后范围逐渐增大，并向抗拖网海床基两侧延伸，冲刷坑的深度逐渐增加。由于抗拖网海床基属于海底结构物，整个平台水平放置到海床面上，且抗拖网海床基对水流起阻碍作用，使得抗拖网海床基周围的水流压缩，导致局部的底流流速增大，从而抗拖网海床基底部周边的泥沙被水流带走。由于泥沙颗粒之间的相互摩擦力所起到阻碍作用，随着水流的冲刷，从冲刷坑内被水流冲走的泥沙愈来愈少，冲刷坑的加深速率逐渐变慢。最后，达到冲刷平衡，冲刷坑的深度不再增加，冲刷的结果如图5所示。从图5中可以清晰地看到从开始时刻到冲刷平衡时冲刷坑形成和床面高度变化的完整过程。

表2 冲刷坑深度随来流时间的变化Tab.2 Changes of scour depth with flow time

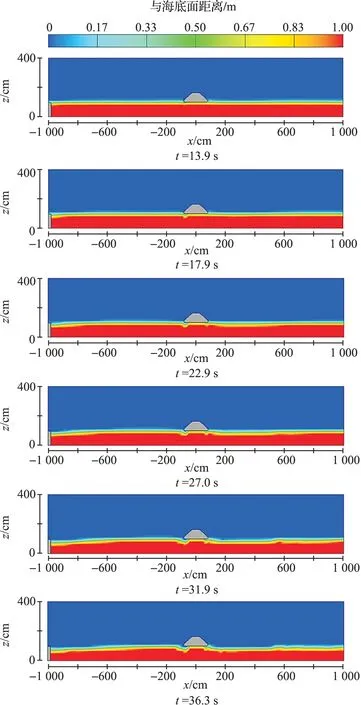
图5 抗拖网海床基沙土基床冲刷坑随时间变化的情况Fig.5 Changes of scour with flow time around Trawl Resistant Seabed Basement

水流遇到抗拖网海床基阻碍时形成了向下的冲击水流，在水流的底部区域会形成与水流行进方向相反的水平方向的反向漩涡(即马蹄形漩涡)，该漩涡对沙土基床冲刷起主要作用。同时因为冲击水流向下的冲击作用，从而在抗拖网海床基迎流区域形成冲刷坑。而在抗拖网海床基背流区域由于向上水流和漩涡的共同作用，泥沙在抗拖网海床基背流区域内被冲刷的效果同样明显。

抗拖网海床基沙土基床冲刷不仅在前后端产生比较明显的冲刷坑，抗拖网海床基左右两侧也会出现明显的冲刷，从图6可以看到，抗拖网海床基左右两侧形成了深度相当的冲刷坑，冲刷坑范围大概在1.8 m左右。在抗拖网海床基底部两端由于马蹄形漩涡和其他小漩涡的作用，抗拖网海床基周围的冲刷坑都比较明显。海床面也发生了相对比较大的变化，抗拖网海床基附近的床面冲刷变化比较大，在距离抗拖网海床基上游0.4 m和下游0.4 m处时，床面基本没变化。图7为冲刷后的抗拖网海床基周围地形的三维图，其中左侧为水流的来流方向。

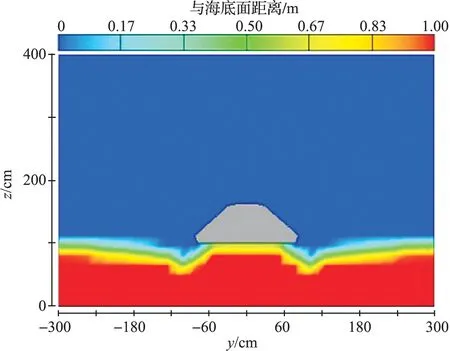
图6 抗拖网海床基两侧的冲刷Fig.6 Scour on the sides of Trawl Resistant Seabed Basement

图7 冲刷后的抗拖网海床基周围地形三维图Fig.7 Three-dimensional map of terrain around Trawl Resistant Seabed Basement after scour

5.2 不同流速下的泥沙冲刷分析

为了更好地研究抗拖网海床基沙土基床的冲刷机理，在模拟中取泥沙粒径d=0.5 mm，分别在行进流速为0.20，0.25，0.30，0.40和0.50 m/s的条件下进行模拟，具体的模拟结果如图8所示。当行进流速为0.20 m/s时，海床面上泥沙不起动，整个模拟过程中，海床面几乎没有变化，冲刷坑深度较小，为4.6 cm。当流速为0.25 m/s时，此时海床面上的泥沙也不起动，但是由于抗拖网海床基阻碍产生的向下阻流，使海床面产生泥沙冲刷，冲刷坑的深度相对较小，为7.52 cm。当流速为0.50 m/s时，海床面上的泥沙起动，最终达到冲刷平衡，其冲刷坑的深度为14.19 cm。

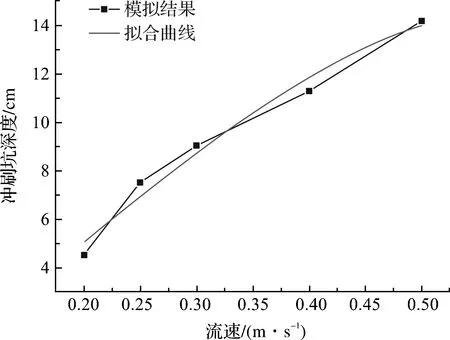
图8 冲刷坑深度随流速的变化Fig.8 Changes of scour depth under different flow velocity

由图9可知，随着流速的增大，抗拖网海床基沙土基床冲刷坑的深度也会相应变大。这是抗拖网海床基沙土基床冲刷坑深度随流速变化的总体趋势。从图中我们可以看到：

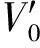
(3)当行进流速V比海床面泥沙的起动流速V0大并且逐渐增大时，在海床面上的泥沙会发生起动，则冲刷坑内会得到上游来沙的补充，冲刷坑的深度由于行进流速的增大而增大的势头会减弱，此时为动床冲刷。随着行进流速V的进一步增大，冲刷坑深度也随之在增大，但是冲刷速率明显减小。图中流速在0.40～0.50 m/s段可大体反映此种趋势。

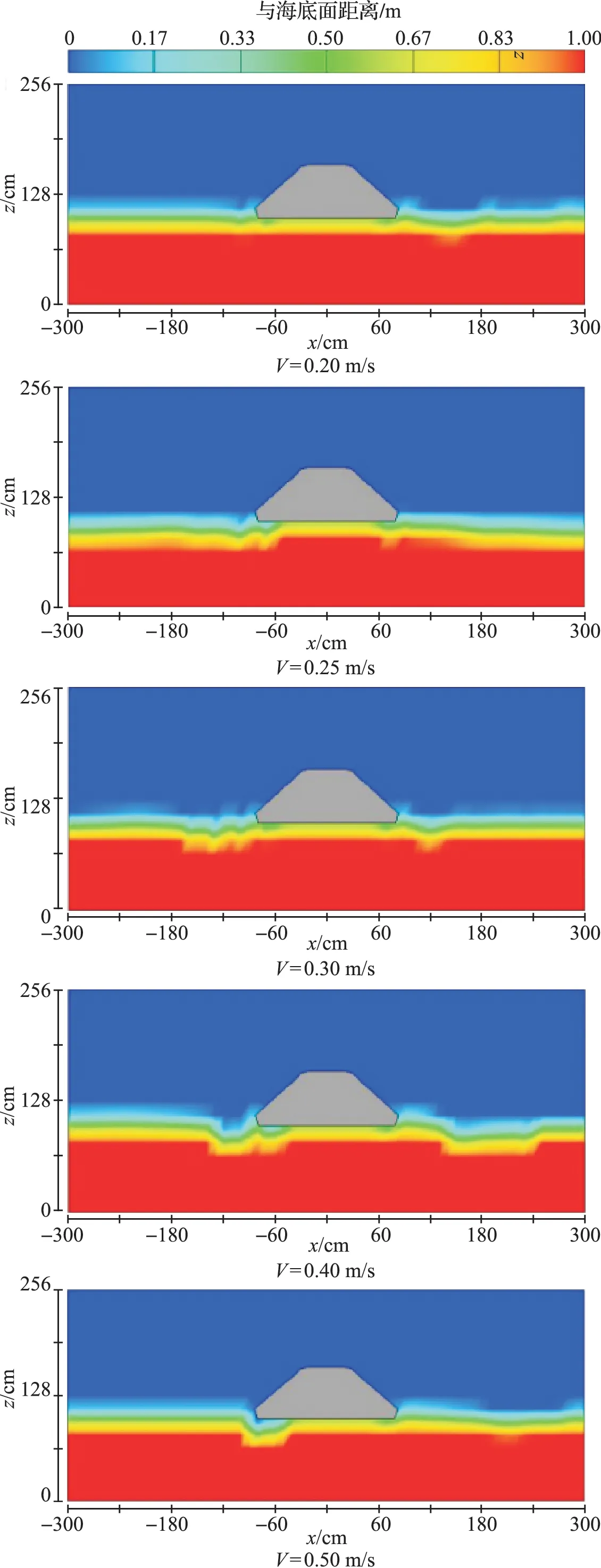
图9 不同流速下抗拖网海床基冲刷模拟图Fig.9 Simulated diagram of scour around Trawl Resistant Seabed Basement under different flow velocity

5.3 不同泥沙粒径下的泥沙冲刷分析

泥沙粒径对抗拖网海床基沙土基床冲刷产生的影响，主要体现在泥沙颗粒的大小、形状、阻力系数和组成结构等四个方面。本文中，设定泥沙颗粒的中值粒径D50分别为0.14，0.20，0.36，0.50和0.65 mm。行进流速设为一个常数，这里选取流速为0.50 m/s。冲刷结果具体见图10和图11。

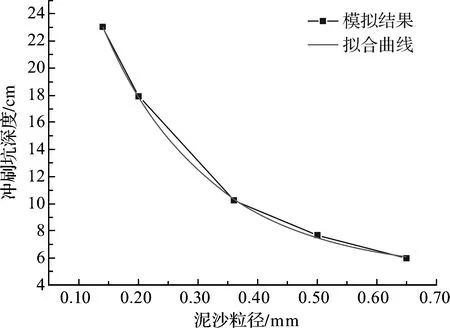
图10 冲刷坑深度随泥沙粒径变化Fig.10 Changes of scour depth under different sand size

但是在实际情况下，由于泥沙粒径不同泥沙冲刷深度不同的现象并不显著。在海底沉积物中，泥沙粒径小则0.1 mm，大则1 000 mm，甚至更大，其比率相差有万倍，有的甚至更多。而抗拖网海床基布放到海底后受海流作用而形成的泥沙冲刷坑的大小不过1.0～15 m，其比率相差仅15倍，前后两者在数量级上差别很大。在数值模拟中，一般都是采用比尺模型进行求解计算，所以冲刷坑大小范围和泥沙颗粒大小范围的变化数量级比较接近。由此可知，数值模拟的结果用于实际应用需要慎重考虑。

6 结论

本文应用Flow-3D软件对抗拖网海床基沙土基床冲刷进行数值模拟，并改变水流流速和泥沙粒径,模拟不同条件下对沙土基床冲刷的影响。

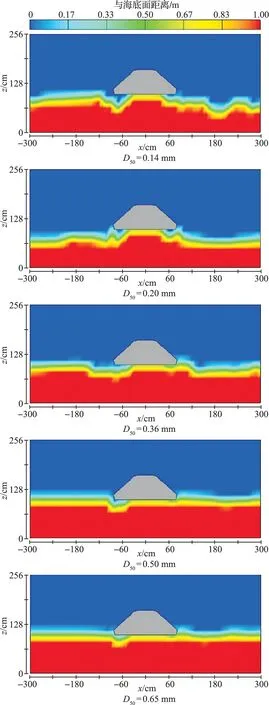
图11 不同泥沙粒径下抗拖网海床基冲刷模拟图Fig.11 Simulated diagram of scour around Trawl Resistant Seabed Basement under different sand size

模拟结果能够直观展现抗拖网海床基沙土基床冲刷坑的形成过程及冲刷床面的变换情况。抗拖网海床基沙土基床冲刷坑深度随海流流速增大而增加，在设定其他条件不改变的情况下，冲刷坑的加深速度随着流速增大会逐渐减缓，最终达到冲淤平衡。在其他条件不变的情况下，随泥沙粒径的增大，冲刷坑深度逐渐减小，而且减小的速度逐渐减缓并趋于不冲刷。

本文的模拟结果还不能完全重现抗拖网海床基布放在海底后冲刷坑的实际情况，这主要是由于海底环境复杂多变，导致模型与实际情况有一定的差异，因此还需要使用更加准确的海床面模型及初始条件对其进行模拟。本研究希望能为抗拖网海床基结构优化设计和实际应用提供理论参考。

[1] LIU Jie, WU Cheng-xuan, LÜ bin, et al. CFD based flow field analysis of a seabed monitoring platform[J]. Shandong Science,2012,25(1)：65-68.

刘杰,吴承璇,吕斌,等.基于CFD的海床基观测平台外部流场分析[J].山东科学,2012,25(1)：65-68.

[2] WANG Fu-jun. Principle and application of CFD software for computational fluid dynamics analysis[M].Beijing:Tsinghua University Press,2004.

王福军.计算流体动力学分析:CFD软件原理与应用[M].北京：清华大学出版社，2004.

[3] XU Jiong-xin, HU Chun-hong, CHEN Jian-guo. The influence of sediment of different size groups on the deposition of the lower reaches of the Yellow River and its significance in the management of the Yellow River[J]. Science in China: Series E,2009,39(2)：310-317.

许炯心，胡春宏，陈建国．不同粒径组泥沙对黄河下游沉积的影响及其在黄河治理中的意义[J]．中国科学:E辑，2009，39(2)：310-317.

[4] ZHAO Yan-fei.Three-dimensional numerical simulation of wave force on the offshore wind turbine structure and scour around foundation[D]. Tianjing:Tianjin University,2010.

赵雁飞.海上风电支撑结构波浪力及基础冲刷的三维数值模拟研究[D].天津：天津大学,2010.

[5] YUAN Yao-chu, ZHAO Jin-ping, WANG Hui-qun, et al. Observations of 450 m currents in the shallow and deep layers of the northeastern South China Sea and their spectral analysis[J]. Science in China: Series D,2002,32(2)：163-176.

袁耀初，赵进平，王惠群，等.南海东北部450 m以浅水层与深水层海流观测结果及其谱分析[J].中国科学:D辑，2002,32(2)：163-176.

NumericalsimulationanalysisofscouraroundTrawlResistantSeabedBasementbasedonFlow-3D

YU Kai-ben1, YANG Tao2, GAO Jian2, LIN Guang-yi2, MENG Qing-jian1, ZONG Le1

(1.NationalDeepSeaCenter,Qingdao266200,China; 2.CollegeofMechanicalandElectricalEngineering,QingdaoScience&TechnologyUniversity,Qingdao266100,China)

Three-dimensional mathematical model of scour around Trawl Resistant Seabed Basement on sand bed was established using Flow-3D. By changing the flow velocity and sediment particle size, the scour on sand bed under different conditions was simulated, and the changes in the trend of maximum scour depth around Trawl Resistant Seabed Basement with the two factors was analyzed. The results show that the scour depth around Trawl Resistant Seabed Basement is increased with current velocity increases, under the other setting conditions unchanged, the scour pit deepened velocity with increasing flow velocity is gradually slowed down, and ultimately achieved sedimentation balance. At the same time, due to the complex and changeable seabed environment, the model and the actual situation are different, and therefore further research should be continued.

Trawl Resistant Seabed Basement；sediment scour；numerical simulation

于凯本，杨涛，高健，等.基于Flow-3D的抗拖网海床基冲刷数值模拟[J].海洋学研究,2017,35(3):91-98,

10.3969/j.issn.1001-909X.2017.03.011.

YU Kai-ben, YANG Tao, GAO Jian, et al. Numerical simulation analysis of scour around Trawl Resistant Seabed Basement based on Flow-3D[J].Journal of Marine Sciences,2017,35(3):91-98, doi:10.3969/j.issn.1001-909X.2017.03.011.

2016-08-15

2016-11-16

“泰山学者工程”专项经费项目资助(tspd 20161007)

于凯本(1977-)，男，山东济南市人，高级工程师，主要从事海洋检测技术方面的研究。E-mail: kedayangtao@163.com

P715.5;P737.2

A

1001-909X(2017)03-0091-08

10.3969/j.issn.1001-909X.2017.03.011