一类四阶偏微分方程的对称约化、精确解和守恒律

张丽香,刘汉泽,辛祥鹏

(聊城大学 数学科学学院,山东聊城 252059)

一类四阶偏微分方程的对称约化、精确解和守恒律

张丽香,刘汉泽,辛祥鹏

(聊城大学 数学科学学院,山东聊城 252059)

利用李群分析研究了一类变系数四阶偏微分方程,求出方程的李点对称,把偏微分方程约化为常微分方程,然后结合(G′/G)展开法及椭圆函数展开法,对约化后的常微分方程求其精确解,从而得到原方程的精确解.进一步,给出这类变系数偏微分方程的守恒律.

变系数方程; 李群分析; 精确解; 守恒律

0 引 言

由于非线性偏微分方程能够描述物理、生物、化学和医学等领域中的复杂现象,而且越来越多的数学、物理和工程问题要转化为非线性偏微分方程的求解问题.因此,研究偏微分方程有重要的意义.而非线性偏微分方程的精确解可以更好地解释某些物理现象.经过多年研究,人们已经提出许多行之有效的方法,比如经典李群方法[1-3],Hirota双线性方法[4-5],修正的CK直接约化方法[6-7],齐次平衡方法[8-10]等.其中李群方法是研究微分方程的有力工具之一,寻找方程的李点对称,由已知解生成新解,从而建立新解和旧解之间的联系.而且这种方法不仅适用于常系数方程和方程组,而且适用于变系数方程.考虑以下变系数四阶偏微分方程

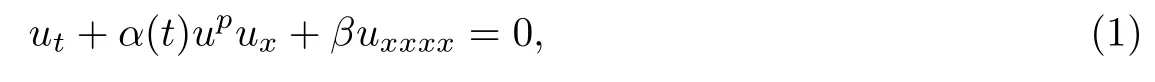
其中u=u(x,t),α(t)为t的函数,β为任意常数,p=1,2,3,···.此类方程尤其在研究弹性梁的弯曲状况和解的稳定性中有重要的意义[11].

本文由以下几部分组成:第1节求出方程(1)的李点对称;第2节,以p=3为例对方程(1)进行约化;第3节,结合(G′/G)展开法[12-14],幂级数展开法[15-16],构造辅助方程[17-18]等方法,对约化后的常微分方程求其精确解,进而得到原方程的精确解;第4节,给出方程(1)的伴随方程和守恒律[19-21];第5节,作简要总结.

1 变系数四阶微分方程的对称

设方程(1)的单参数向量场为

其中ξ(x,t,u),τ(x,t,u),ϕ(x,t,u)为待定函数.若向量场(2)为方程(1)的李点对称,则

下面根据α(t)的取法不同讨论(5),得到方程(1)的生成元.

情况(i)

则生成元为

情况(ii)

(1)当4tα′(t)+3α(t)=0时,即α(t)=(k为非零常数),

则生成元为

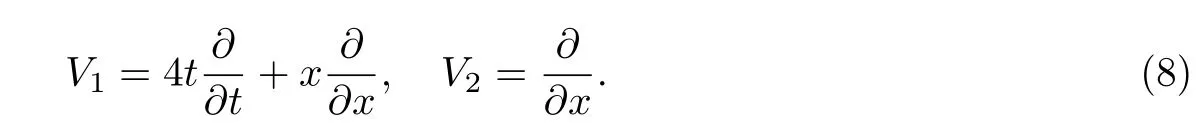
(2)当4tα′(t)+3α(t)/=0时,有下列几种子情况.

(a)α′(t)=kpα(t),即α(t)=lekpt(k为非零常数),

则生成元为

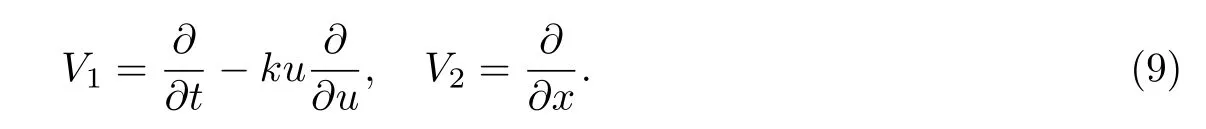
(b)4tα′(t)+3α(t)=kα′(t),即α(t)=l(4t− k)(k,l为非零常数),

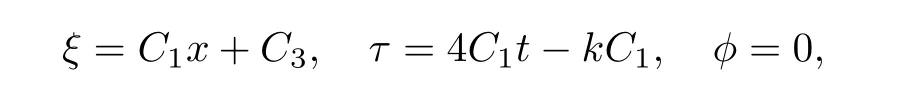
则生成元为

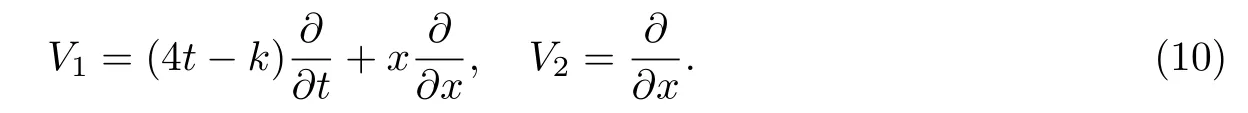
(c)4tα′(t)+3α(t)=kpα(t),即α(t)=lt(k,l为非零常数),

则生成元为

(d)C1=C2=C4=0,即α(t)为关于t的任意函数.

2 变系数四阶微分方程的对称约化

前文中我们已经求出了方程(1)的李点对称,下面以p=3为例,对方程(1)进行约化.

2.1 情况(i)

当α′(t)=0时,即α(t)=k(k为非零常数),方程(1)退化为常系数四阶偏微分方程

其中f′=df/dξ.

(b)对于向量场V=V2+cV3=∂t+c∂x,对应的群不变解为u=f(ξ),其中ξ=x−ct,将其代入方程(12),得约化方程为

其中f′=df/dξ.

2.2 情况(ii)

(1)当4tα′(t)+3α(t)=0时,即α(t)=(k为非零常数),方程(1)变为

对于向量场V1=4t∂t+x∂x,对应的群不变解为u=f(ξ),其中ξ=,将其代入方程(15),得约化方程为

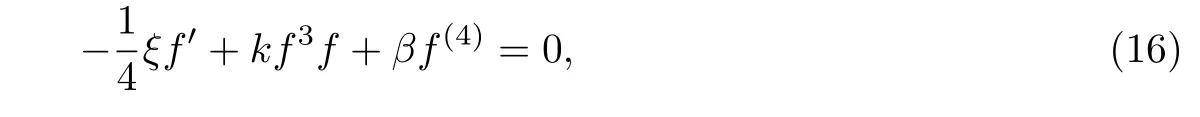
其中f′=df/dξ.

(2)当4tα′(t)+3α(t)/=0时,有下列几种子情况.

(a)α′(t)=kpα(t),即α(t)=lekpt(k为非零常数),方程(1)变为

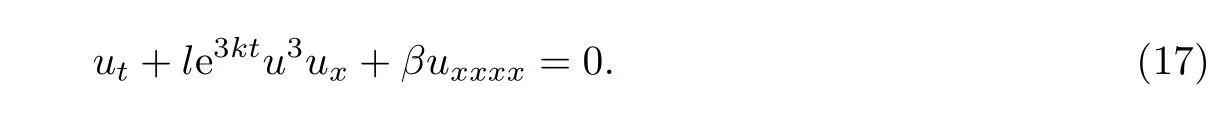
对于向量场V1=∂t−ku∂u,对应的群不变解为u=f(ξ)e−kt,其中ξ=x,将其代入方程(17),得约化方程为

其中f′=df/dξ.

(b)4tα′(t)+3α(t)=kα′(t),即(k,l为非零常数),方程(1)变为

对于向量场V1=(4t− k)∂t+x∂x,对应的群不变解为u=f(ξ),其中将其代入方程(19),得约化方程为

其中f′=df/dξ.约化后的方程(20)和方程(16)形式相同.

(c)4tα′(t)+3α(t)=kpα(t),即(k,l为非零常数),方程(1)变为

对于向量场V1=4t∂t+x∂x−k∂u,对应的群不变解为其中将其代入方程(21),得约化方程为

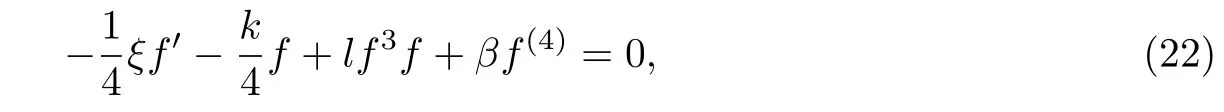
其中f′=df/dξ.

(d)C1=C2=C4=0即α(t)为关于t的任意的函数.方程(1)的群不变解为u=f(t),将其代入方程(1)得f′(t)=0.易得方程(1)的精确解为u=C,其中C为任意常数.

3 变系数四阶偏微分方程的精确解

前文中,我们通过讨论α(t)的不同情况,已经得到了约化方程.本节中,我们结合椭圆函数展开法、(G′/G)展开法及幂级数展开法等对约化后的方程(13)、(14)、(16)和(18)求其精确解,进而得到方程(1)的精确解,包括精确幂级数展开解,椭圆函数展开解及三角函数解等.

3.1 方程(13)的精确解

对方程(13)积分一次,得

其中A0是积分常数.假设方程(23)有以下形式的解

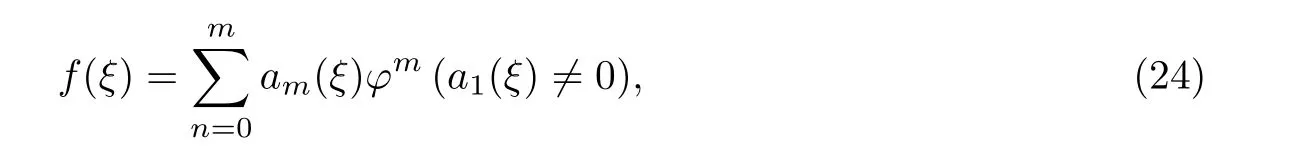
由齐次平衡原理得m=1,故方程(24)有以下形式的解,且

其中φ是Riccati方程的已知解

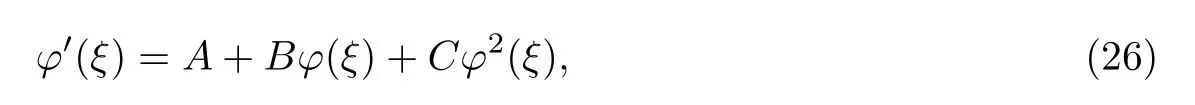
其中A=A(ξ),B=B(ξ),C=C(ξ).

把式(25)、(26)代入方程(23)中,比较φi(i=0,1,2,3,4)的同次幂系数得

当λ2−4µ＜0时,方程(23)的精确解为

其中C1,C2均为任意常数,B=B(ξ),C=C(ξ).

3.2 方程(14)的精确解

对方程(14)积分一次得

其中B0为积分常数.假设方程(27)有如下形式的解

由齐次平衡原理得m=1.故方程(27)有如下形式的解

其中k1,k0为待定常数,φ(ξ)是Riccati方程的已知解,且

其中A,B,C是常数.把式(29)、(30)代入方程(27)中,收集φi(i=0,1,2,3,4)的各项系数,并且令各项系数为零,得到关于k1,k0的代数方程组,解方程组得

故方程(27)的解为

对于方程(14)的解

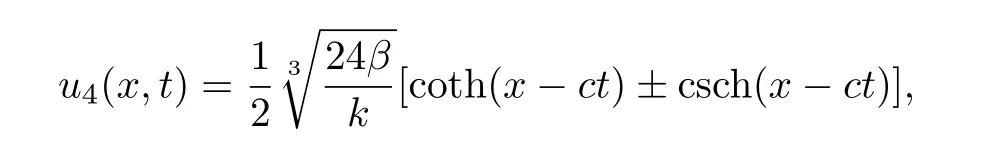
借助Maple软件,u4(x,t)的图像如图1所示.

对于方程(14)的解

图1=2,c=2,x∈ [−10,20],t∈ [0,1]时,u4为双孤子解Fig.1 When=2,c=2,x ∈ [−10,20],t∈ [0,1],u4is double soliton solution

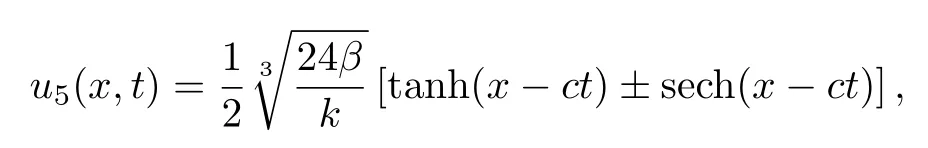
u5(x,t)的图像如图2所示.

对于方程(14)的解

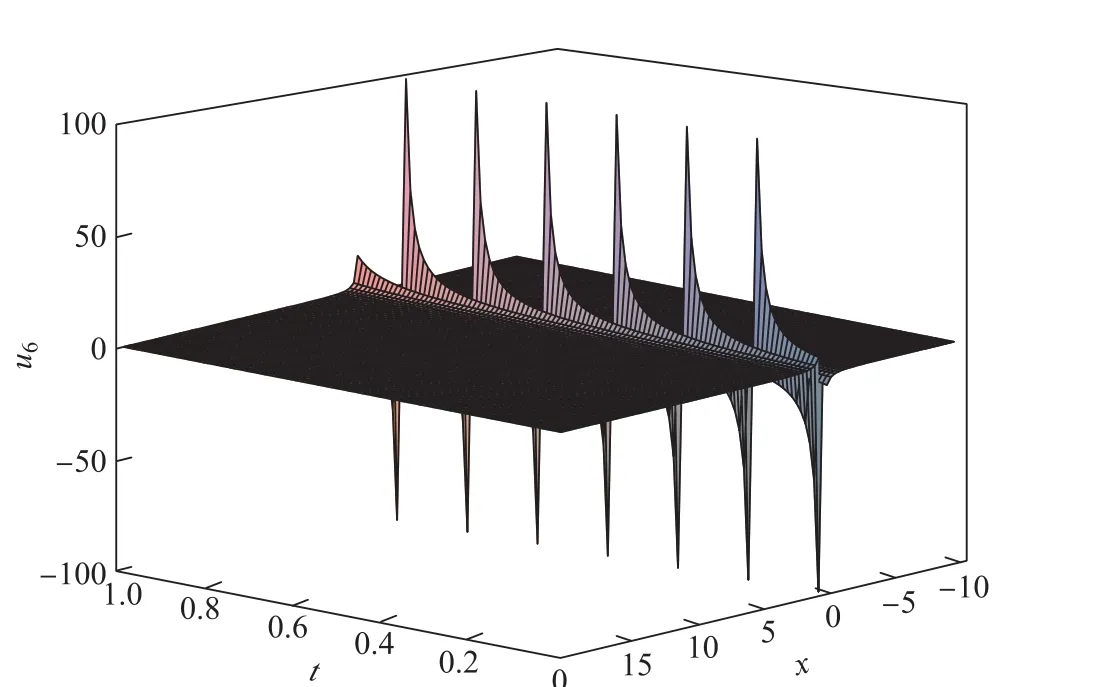
u6(x,t)的图像如图3所示.

对于方程(14)的解

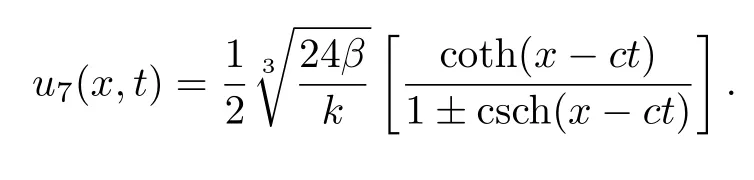
u7(x,t)的图像如图4所示.

图2=2,c=2,x∈[−10,20],t∈[0,1]时,u5为凹尖峰孤子解Fig.2 When=2,c=2,x ∈ [−10,20],t∈ [0,1],u5is concave peak soliton solution

3.3 方程(16)的幂级数解

假设方程(16)有如下形式的幂级数展开解

把式(31)代入方程(16)中,得

比较式(32)中的系数,可得:当n=0时,C4=

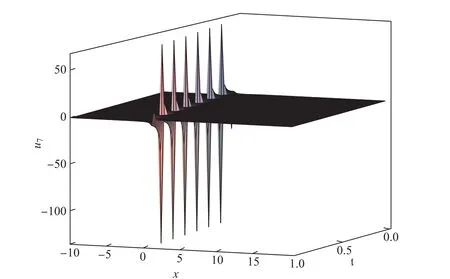
图4=2,c=2,x∈ [−10,20],t∈ [0,1]时,u7为双孤子解Fig.4 When=2,c=2,x ∈ [−10,20],t∈ [0,1],u7is double soliton solution

当n≥1时,

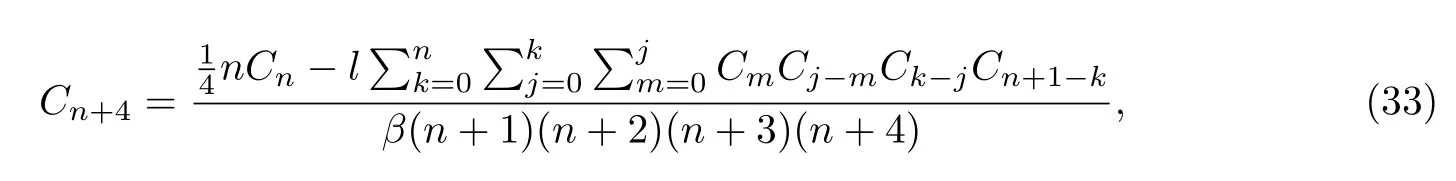
其中C0,C1,C2,C3为任意常数.由(33)式可得

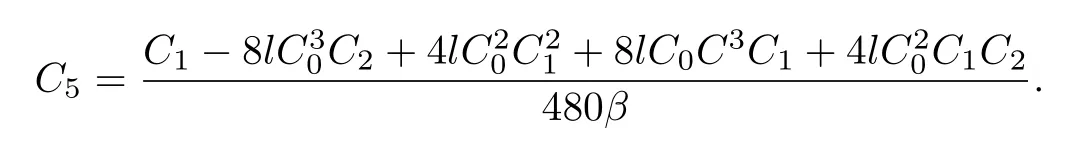
故方程(16)的解为

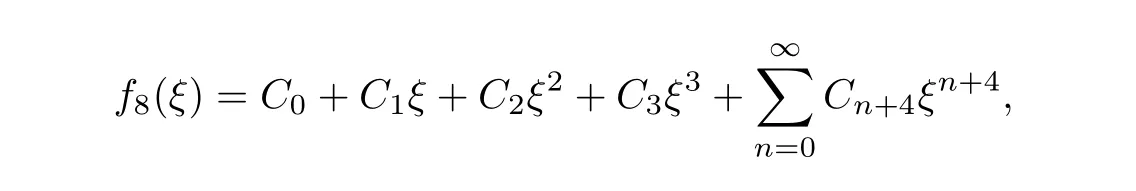
因此得原方程(15)的精确幂级数展开解为

其中C0,C1,C2,C3为任意常数,Cn+4由(33)式确定.

3.4 方程(18)的精确解

其中G=G(ξ),且满足二阶线性常微分方程

由式(34)和(35)得

把式(34)–(38)代入方程(18),平衡最高阶导数项f(4)和最高阶非线性项f3f′的次数,得m=1,故方程(18)有如下形式的解

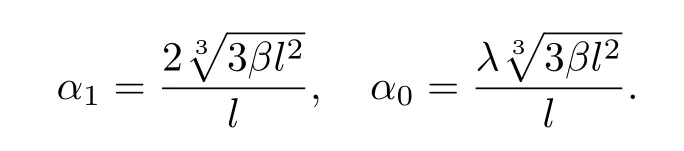
当λ2−4µ＞0时,方程(18)的精确解为

故方程(17)的精确解为

故方程(17)的精确解为

当λ2−4µ=0时,方程(18)的精确解为

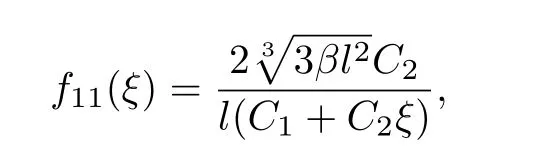
故原方程(17)的精确解为

其中C1,C2均为常数.

4 变系数四阶微分方程的伴随方程和守恒律

在这一部分,我们将给出方程(1)的伴随方程和守恒律.

方程(1)的伴随方程为

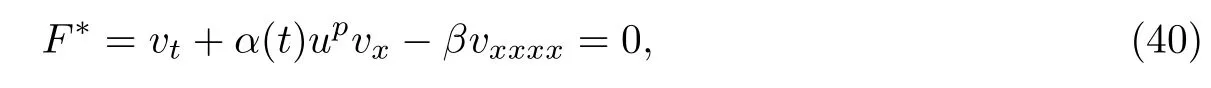
设v=ψ(x,t,u),且ψ(x,t,u)/=0.根据Ibragimov给出的定义

其中F=ut+α(t)upux+βuxxxx=0.把式(40)、(41)入方程(1),得

比较ux,ut,u2x,···的系数得,ψ=ρ,其中ρ为非零常数.

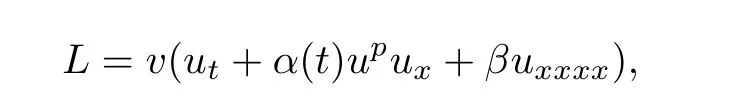
利用Ibragimov给出的结论,守恒向量为

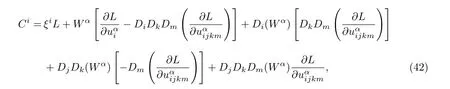
其中Wα=.

根据Ibragimov给出的结论,给出向量场的通式

那么方程(1)的守恒律由下式决定

向量场C=(C1,C2)由下式决定

以下面情况(i)和情况(ii)为例,可分别求出显式守恒律.

情况(i)

考虑方程(12),对于向量场

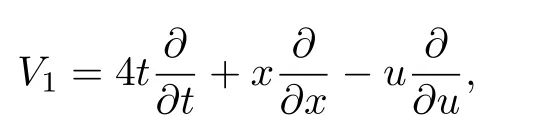
有W=−(u+4tut+xux),

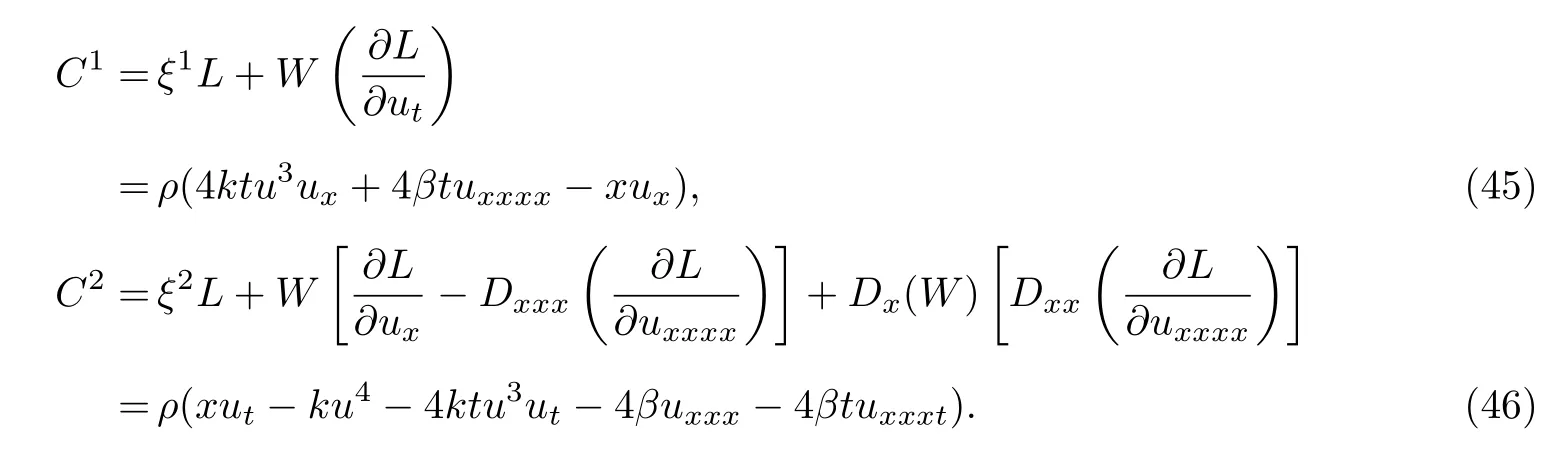
情况(ii)

考虑方程(17),对于向量场

有W=−(ku+ut),

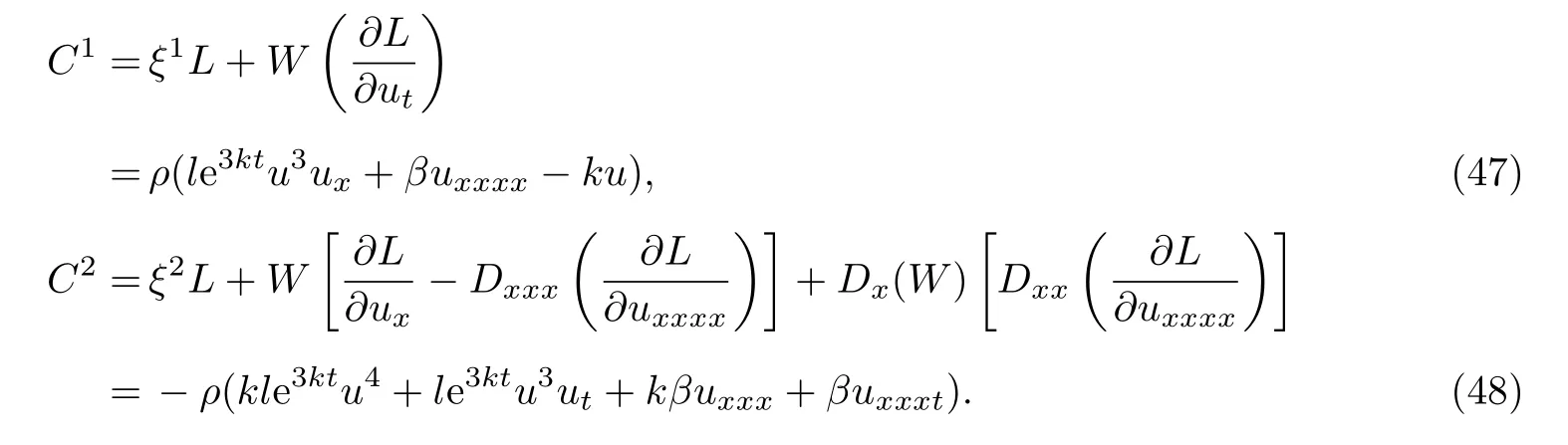
以上守恒向量C=(C1,C2)包含了伴随方程(40)的任意解ρ,因此给出了方程的无穷多个守恒律.

5 结 论

本文运用李群分析研究了一类变系数四阶偏微分方程,把复杂的偏微分方程约化成常微分方程,通过求常微分方程的精确解,得到原方程的精确解,包括三角函数解,幂级数展开解,椭圆函数解等.进而可以建立新解和旧解之间的关系,能更好地解释复杂的物理现象.李群是研究微分方程的有力工具之一,无论是研究常系数偏微分方程还是变系数偏微分方程,都具有广泛的应用.另外,我们给出了四阶变系数方程的伴随方程和显式守恒律.

[1] 田畴.李群及其在微分方程中的应用[M].北京:科学出版社,2001.

[2] OLVER P.Applications of Lie Groups to Differential Equations[M].New York:Springer,1993.

[3] BLUMAN G,ANCO S.Symmetry and Integration Methods for Differential Equations[M].New York:Springer-Verlag,2002.

[4]HIROTA R,SATSUMA J.A variety of nonlinear network equations generated form the B¨acklund transformation for the Tota lattice[J].Suppl Prog Theor Phys,1976,59:64-100.

[5] LIU H Z,LI J B,CHEN F J.Exact periodic wave solutions for the mKdV equations[J].Nonlinear Anal,2009,70:2376-2381.

[6] WANG G W,XU T Z,LIU X Q.New explicit solutions of the fifth-order KdV equation with variable co´efficients[J].Bull Malays Math Sci Soc 2014,37(3):769-778.

[7] 胡晓瑞.非线性系统的对称性与可积性[D].上海:华东师范大学,2012,43-77.

[8] 刘大勇,夏铁成.齐次平衡法寻找Caudrey-Dodd-Gibbon-Kaeada方程的多孤子解[J].应用数学和计算数学学报,2011,25(2):205-212.

[9] 刘丽环,常晶,冯雪.求非线性发展方程行波解的(G′/G)展开法[J].吉林大学学报(理学版),2013,51(2):183-186.

[10] 张辉群.齐次平衡方法的扩展及应用[J].数学物理学报,2001,21A(3):321-325.

[11] YAO Q L.Existence,multiplicity and infinite solvability of positive solutions to a nonlinear fourth-order periodic boundary value problem[J].Nonlinear Analysis,2005,63:237-246.

[12] WANG M L,LI X Z,ZHANG J L.The(G′/G)-expansion method and travelling wave solutions of nonlinear evolution equations in mathematical physics[J].Phys Lett A,2008,372:417-423.

[13] 赵烨,徐茜.一类耦合Benjamin-Bona-Mahony型方程组的新精确解[J].纯粹数学与应用数学,2015,31:12-17.

[14] LI K H,LIU H Z.Lie symmetry analysis and exact solutions for nonlinear LC circuit equation[J].Chinese Journal of Quantum Electronics,2016,33:279-286.

[15] 杨春艳,李小青.一类四阶偏微分方程的对称分析及级数解[J].纯粹数学与应用数学,2016,32:432-440.

[16] 徐兰兰,陈怀堂.变系数(2+1)维Nizhnik-Novikov-Vesselov的三孤子新解[J].物理学报,2013,62(9):090204(1-6).

[17] 魏帅帅,李凯辉,刘汉泽.展开法在Riccati方程中的应用[J].河南科技大学学报.2015,36:92-96.

[18] IBRAGIMOV N H.Integrating factors,adjoint equations and Lagrangians[J].J Math Anal Appl,2006,38:742-757.

[19] IBRAGIMOV N H.A new conservation theorem[J].J Math Anal Appl,2007,333:311-328.

[20] IBRAGIMOV N H.Nonlinear self-adjointness and conservation laws[J].J Phys A,2011,44:432002(899).

[21] ROSA R,GANDARIAS M L,BRUZON M S.Symmetries and conservation laws of a fifth-order KdV equation with time-dependent coefficients and linear damping[J].Nonlinear Dyn,2016,84:135-141.

[22] YOMBA E.On exact solutions of the coupled Klein-Gordon-Schr¨odinger and the complex coupled KdV equations using mapping method[J].Chaos,Solitons and Fractals,2004,21:209-229.

(责任编辑:林 磊)

Symmetry reductions,exact solutions and conservation laws of a class of forth-order partial differential equations

ZHANG Li-xiang,LIU Han-ze,XIN Xiang-peng
(School of Mathematical Sciences,Liaocheng University,Liaocheng Shandong 252059,China)

The partial differential equation with constant coefficients can merely approximately reflect the law of motion of substances.Relatively the partial differential equation with variable coefficients can reflect the complex movement of substances more accurately. Therefore,it is more important to study the partial differential equations with variable coefficients. This paper investigates a class of variable coefficient partial differential equations.By using Lie symmetry analysis,the symmetries of the equations are obtained,Then the partial differential equations are reduced to ordinary differential equations.Moreover,we combine with(G′/G)expansion method and elliptic function expansion,so exact solutions to the original equation are obtained.Furthermore,the conservation laws of this kind of variable coefficient differential equations are given.

variable coefficient equation;Lie symmetry analysis;exact solution;conservation law

O175.2

A

10.3969/j.issn.1000-5641.2017.06.005

1000-5641(2017)06-0050-13

2016-12-14

国家自然科学基金(11171041,11505090)

张丽香,女,硕士研究生,研究方向为微分方程理论及应用.E-mail:244630623@qq.com.

刘汉泽,男,教授,研究方向为微分方程理论及应用.E-mail:hnz liu@aliyun.com.