电离层延迟高阶项对GPS精密单点定位精度影响分析

秦姗兰,王文萍,庄文泉

(中国地震局第二监测中心,陕西 西安 710054)

电离层延迟高阶项对GPS精密单点定位精度影响分析

秦姗兰,王文萍,庄文泉

(中国地震局第二监测中心,陕西 西安 710054)

随着GPS卫星轨道、钟差及各种误差修正模型的不断精化,静态精密单点定位(PPP)定位精度达到mm级,进行电离层延迟高阶项较小量级的误差改正研究,对改进PPP数据处理策略具有重要的参考价值。本文利用分布在不同地理纬度的5个IGS跟踪站3天的观测数据,对比分析了电离层延迟二阶项、三阶项对GPS观测值精度及静态PPP定位精度的影响。分析结果表明,电离层延迟二阶项、三阶项对GPS观测值精度的影响分别为cm级和mm级,对低纬度地区PPP定位精度的影响大于3 mm,但对中高纬度的测站观测值、定位精度的影响比低纬度地区小很多。

电离层延迟高阶项;精密单点定位;精度

0 引 言

精密单点定位技术(PPP)是全球定位技术(GPS)高精度定位的主要手段之一,在大地测量、海洋测量等诸多领域得到广泛应用[1-4]。电离层延迟误差是影响GPS观测值精度的主要因素之一,其引起的距离测量误差最大可达上百米量级[1,4-5]。当前PPP定位中采用双频消电离层组合消除了电离层延迟一阶项,不考虑电离层高阶项的影响。目前,随着卫星精密轨道、卫星钟差精度的不断提高和各种误差修正模型的不断精化,PPP双频静态事后解算精度达到mm级[6-7],电离层高阶项延迟误差、多路径效应误差等相对较小误差的修正在GPS mm级精度应用中已被重视。已有学者针对电离层高阶项延迟进行研究, Marques等研究了电离层高阶项对GPS观测值精度的影响[8];张双城等应用西安地区的GPS双频观测数据分析了电离层二阶项随时间的变化规律[9];武岳等基于GPS三频观测值进行电离层延迟二阶项进行修正[10];刘西凤等给出了电离层高阶项对GPS相对定位的影响[11]。上述研究大多数集中在电离层高阶项对GPS观测值精度的影响和电离层延迟高阶项误差改正方法,针对电离层高阶项对PPP定位精度影响的研究成果相对较少[12],有待进一步研究。本文首先给出了电离层延迟高阶项的计算方法与计算流程,并用实测数据分析了电离层延迟高阶项对观测值的影响,重点研究了电离层延迟高阶项对PPP定位精度的影响。

1 电离层延迟高阶项计算方法

目前常用双频无几何组合计算测量信号在卫星到接收机传播路径上的电离层延迟,该方法使用的前提是忽略电离层延迟高阶项对观测值的影响,但近年来的研究结果表明,电离层高阶项的影响可达到2～4 cm[13].顾及电离层高阶项对GPS观测的影响,GPS观测方程可写为[14-15]

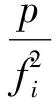
(1)

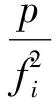
(2)

其中

(3)

≈2.2566×1012Bcosκ×TEC，

(4)

(1+cos2κ)ds

≈1602.7491×Nm×TEC，

(5)

式中:i为GPS系统的频率标识;f为频率值(f1=1 575.42 MHz,f2=1 227.60 MHz);λ为载波相位观测值的波长;N为对应载波相位观测值的模糊度;ρ为卫星和接收机间的几何距离;B为电离层穿刺点处的地磁感应强度;κ为卫星信号矢量与地磁感应强度矢量在穿刺点处的夹角;Ne为电离层电子密度;εP和εΦ分别为码和载波相位观测值未被模型化的残余误差; ds为积分路径;Nm为在电离层高度的最大电子含量;TEC为穿刺点处的电离层电子含量,可通过双频码伪距无几何组合得到

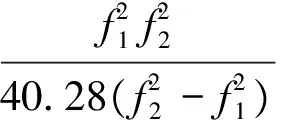
c(DCBr+DCBS)+ε12) ，

(6)

式中,DCBr、DCBS分别为接收机、卫星码间偏差(ns);c为光速(m/s);ε12为双频无几何组合观测噪声(m)。

从式(1)和式(2)可以看出,载波相位和码的电离层延迟一阶项大小相等,符号相反;码的电离层延迟二阶项是载波相位的2倍,符号相反;码的电离层延迟三阶项是载波相位的3倍,符号相反。

图1示出了电离层延迟高阶项的计算流程。首先进行粗差剔除、周跳探测等数据预处理,获得相位平滑伪距的观测值;其次组成双频无几何组合,计算得到穿刺点处电离层TEC;最后输入穿刺点处的地磁感应强度、电离层TEC等参数,得到电离层二阶项、三阶项对码和载波相位观测值影响的具体数值,并直接修正至原始观测文件中,输出新的观测文件供PPP定位使用。

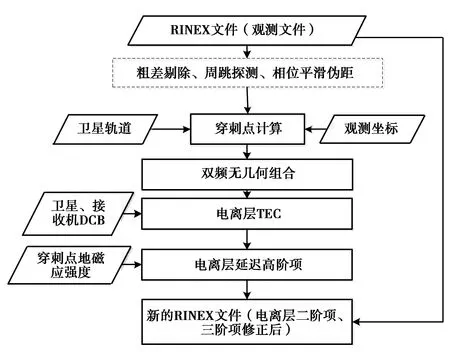
图1 电离层延迟高阶项计算流程

2 结果分析

实验数据选取5个IGS连续跟踪站(跟踪站详细信息见表1)2013-1-7～2013-1-9日3天GPS双频观测数据进行分析,采样间隔为30 s,截止高度角为10°.从表1可以看出,5个跟踪站分布在不同的地理纬度,且均安装了高性能接收机与扼流圈天线,可保证采集高质量的观测数据,下面重点分析电离层高阶项对观测值精度和对PPP定位精度的影响。

表1 跟踪站信息

2.1电离层延迟高阶项对观测值精度的影响

按照式(1)～(6)示出的理论方法与图1给出的计算流程,计算了2013年1月7日的5个测站电离层延迟的高阶项。计算过程中所需的电离层TEC值采用双频相位平滑伪距观测量计算得到,卫星和接收机DCB采用国际GNSS服务(IGS)提供的最终产品,卫星轨道从广播星历计算得到,测站坐标采用BERNESE软件计算[16],地磁感应强度参数B及与卫星信号间的夹角κ采用国际地磁标准IGRF 11模型计算得到[17]。

选取五个跟踪站分布在不同的地理纬度,BRFT站位于赤道附近,GUAO位于中纬度地区。图2示出了两站电离层二阶项、三阶项对GPS L1和GPS L2观测值精度的影响结果,横坐标为协调世界时(2013年1月7日),纵坐标为电离层高阶项对观测值的影响。可以看出,位于赤道附近的BRFT站的电离层延迟二阶项、三阶项对观测值的影响明显大于位于中纬度的GUAO站,电离层二阶项对观测值的影响在cm级,在赤道附近的峰值达到3 cm;电离层三阶项对观测值的影响在mm级,在赤道附近的峰值小于5 mm.结合其他几个站的计算结果看,电离层高阶项对观测值的影响具有随地理纬度分布的特征,在低纬度地区影响大,中高纬度地区影响比低纬度地区小很多。

图2 电离层延迟高阶项对GPS观测值的影响(a)信号传播路径上的电离层电子含量(电离层延迟一阶项)(b)电离层延迟二阶项对L1观测值的影响,(c)电离层延迟二阶项对L2观测值的影响(d)电离层延迟三阶项对L1观测值的影响; (e)电离层延迟三阶项对L2观测值的影响;

从电离层延迟二阶项、三阶项在一天内的变化看,二者与电离层TEC有相同的变化趋势,在当地时间午后14时左右达到最大峰值,在当地时间的夜间变化较为平缓,这与当地的太阳辐射强度相关。

电离层二阶项、三阶项对GPS L1频率的影响明显小于L2频率,结合式(1)分析,电离层延迟一阶项、二阶项、三阶项与观测频率的平方成反比例,GPS L2的频率值小于L1,电离层对L2观测值的影响大于L1观测值。

2.2电离层高阶项对精密单点定位精度影响

利用2.1节电离层高阶项修正后的观测数据与原始观测数据分别进行静态PPP解算,解算参数包括站坐标、接收机钟差、对流层延迟湿分量等参数,卫星精密星历、精密钟差、DCB、天线相位中心等产品从IGS下载得到,电离层延迟一阶项采用无电离层组合法消除,电离层延迟二阶项、三阶项采用模型改正。

图3示出了5个测站3天定位结果在N、E、U3个方向上的差异,图中纵坐标表示电离层延迟高阶项修正前后PPP定位结果在N、E、U方向的差异,横坐标表示测站,测站纬度从北向南由高到低依次排列。从图中可以看出电离层延迟高阶项对静态PPP定位结果有明显影响,从影响量级来看,电离层延迟高阶项对BRFT站PPP定位精度的影响明显大于其它测站,这2.1节与电离层高阶项对观测值精度的影响分析结果向匹配。电离层高阶项对位于赤道附近BRFT站PPP定位精度的影响大于为3 mm,对位于中纬度地区的CUT0和GUAO站的影响约为1 mm,对位于南北极附近的NRIL和CAS1站的影响小于1 mm.结合电离层延迟二阶项、三阶项对观测值精度的影响量级分析,在低纬度地区进行mm级需求静态PPP定位精度解算时,可忽略电离层延迟三阶项的影响,但进行电离层延迟二阶项改正是十分必要的;在中高纬度地区,电离层延迟高阶项的影响很小,可忽略不计。

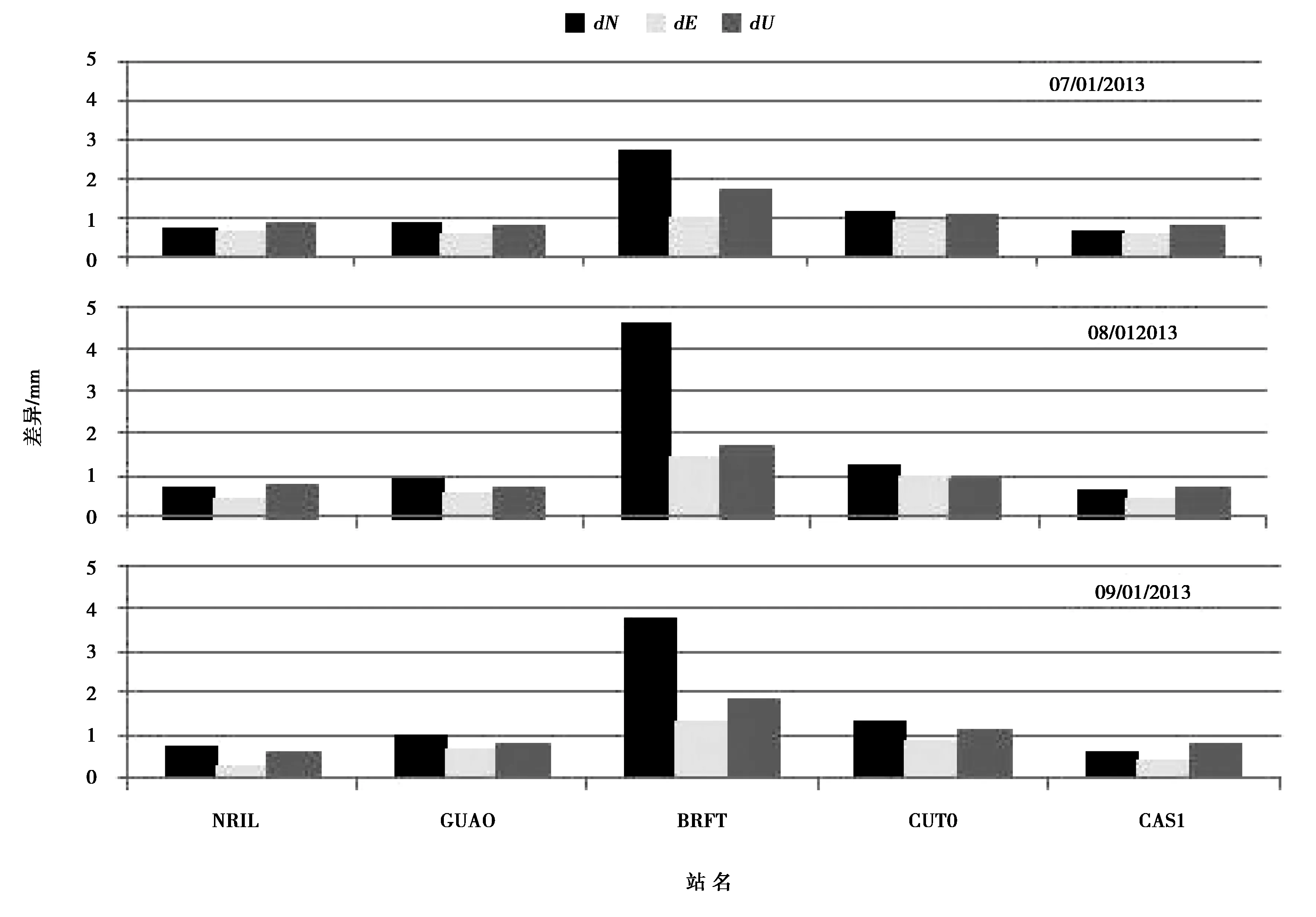
图3 电离层延迟高阶项对PPP定位精度的影响

3 结束语

本文给出了电离层延迟高阶项对GPS观测值精度影响量级,对比分析了电离层高阶项修正前后PPP定位精度的差异。电离层二阶项和三阶项对GPS观测值精度的影响分别为cm级和mm级,且在赤道附近(低纬度地区)的影响程度明显大于中高纬度地区。电离层高阶项对低纬度地区PPP定位精度的影响大于3 mm,对中纬度地区PPP定位精度的影响约为1 mm,对高纬度地区PPP定位精度的影响小于1 mm.因此,在低纬度地区,PPP技术要在地壳形变监测、板块运动测量、大型建筑物变形监测等mm级定位中使用,必须进行电离层延迟高阶项修正,尤其是电离层延迟二阶项。

[1] HOFFMANN-WELLENHOF B, LICHTENEGGER H, COLLINS J. Global positioning system: theory and practice[M]. Springer, New York, 2001.

[2] 邓连生,姜卫平,李昭,等.电离层高阶项改正对参考框架实现及测站坐标的影响分析[J].武汉大学学报(信息科学版),2015,40(2):193-198.

[3] ZHANG X H, ANDERSEN O B. Surface ice flow velocity and tide retrieval of the amery ice shelf using Precise Point Positioning[J]. Journal of Geodesy, 2006(80): 171-176.

[4] 李征航,张小红.GPS卫星导航定位新技术及高精度数据处理方法[M].武汉:武汉大学出版社,2009.

[5] 袁运斌,欧吉坤.利用GPS研究电离层延迟及电子浓度变化规律[J].全球定位系统,2001,36(1):19-21.

[6] ZHAO X, WANG S, LIU C,etal. Assessing the performance of multi-GNSS precise point positioning in Asia-Pacific region[J]. Survey Review, 2017,354(49):186-196.

[7] GÉRARD LACHAPELLE, PETOVELLO M. Precise Point Positioning and its challenges, aided-GNSS and signal tracking[J]. InsideGNSS, 2006(8):16-18.

[8] MARQUES H.A, MONICO J F G.RINEX-H O: second-and third-order ionospheric corrections for RINEX observation files[J]. GPS Solutions, 2011(15):305-314.

[9] 张双成,涂锐,张勤,等.电离层二阶项模型的构建及其变化规律分析研究[J].测绘学报,2011,40(Sup.):105-110.

[10] 伍岳,孟泱,王泽民,等.GPS现代化后电离层折射误差高阶项的三频改正方法[J].武汉大学学报(信息科学版),2005,30(7):601-603.

[11] 刘西凤,袁运斌,霍星亮.电离层二阶项延迟对GPS定位影响的分析模型与方法[J].科学通报,2010,55(12): 1162-1167.

[12] 张小红,任晓东,郭斐.顾及电离层延迟高阶项改正的精密单点定位[J]. 武汉大学学报(信息科学版),2013, 38(8):883-887.

[13] 魏子卿,葛茂荣.GPS相对定位的数学模型[M]. 北京: 测绘出版社, 1998.

[14] HERNA'NDEZ-PAJARES M, JUAN J M, SANZ J. Second-order ionospheric term in GPS: implementation and impact on geodetic estimates[J]. Journal of Geophysical Research Solid Earth, 2007(112): 1-16.

[15] KEDAR S, HAJJ A, WILSON B D, HEFLIN M B. The effect of the second order GPS ionospheric correction on receiver positions[J]. Geophysical Research Letters, 2003,30(16):1829. Doi:10.1029/2003.GL017639.

[16] DACH R, LUTZ S, WALSER P,etal. Bernese GNSS software version 5.2. user manual[M]. Astronomical Institute, Universtiy of Bern, Bern Open Publishing. 2015.

[17] 黄晓颖,边少锋.国际高精度地磁模型研究进展[J].海洋测绘,2010,30(3): 79-82.

AnInfluenceAnalysisofHigh-orderIonosphereonGPSPrecisePointPositioning

QINShanlan,WANGWenping,ZHUANGWenquan

(SecondMonitoringandApplicationCenter,ChinaEarthquakeAdministration,Xi′an710054,China)

With the continuous refinement of GPS satellite orbit, clock error and various error correction models, carrying out the study on the high-order ionospheric error correction of static Precision Point Position (PPP), which has an important reference value for improving the processing strategy of PPP observations. The influence degree of high-order ionospheric error on the accuracy of GPS observations and static PPP is analyzed and compared, using the observations from 5 IGS tracking stations, during January 7-9, 2013. The results show that: 1) the influence of the second-order and the third-order of the ionospheric error on the accuracy of GPS observation are cm level and mm level, respectively; 2) the influence of the high-order ionospheric error on the accuracy of GPS PPP is more than 3 mm in low latitude. But the influence degree on the accuracy of the observations and PPP in middle and high latitudes is much smaller than that in low latitudes.

High-order ionospheric delay; PPP; precision

10.13442/j.gnss.1008-9268.2017.05.007

P228.4

A

1008-9268(2017)05-0033-06

2017-10-09

国家自然科学基金(批准号:51479163)和地震行业科研专项(编号:201508009)

联系人: 秦姗兰 E-mail: shanlan_qin@163.com

秦姗兰(1984-),女,硕士,工程师,主要从事GNSS数据处理与分析工作。

王文萍(1965-)，女，高级工程师，主要从事数据分析研究。

庄文泉(1990-)，男，硕士,助理工程师，主要从事GNSS数据处理与应用。