基于IGGIII模型的高精度抗差坐标转换算法研究

张洋,张志刚,钱栋,黄岩松,于龙昊

(1.苏州地质工程勘察院,江苏 苏州 215129; 2.南京市测绘勘察研究院股份有限公司,江苏 南京 211100, 3.北京建筑大学 测绘与城市空间信息学院,北京 102616)

基于IGGIII模型的高精度抗差坐标转换算法研究

张洋1,张志刚1,钱栋1,黄岩松2,于龙昊3

(1.苏州地质工程勘察院,江苏 苏州 215129; 2.南京市测绘勘察研究院股份有限公司,江苏 南京 211100, 3.北京建筑大学 测绘与城市空间信息学院,北京 102616)

针对经典空间直角坐标转换没有考虑公共点坐标精度对求解坐标转换参数的影响,提出了一种基于稳健抗差估计理论的空间直角坐标转换方法,该方法采用IGGIII模型对精度较低或误差过大的公共点重新定权,逐渐降低其在求解坐标转换参数中的作用,进而获得可靠的坐标转换参数。最后利用编制的算法程序对某工程实例中的公共点坐标数据进行计算,结合设计的两个方案对比分析表明本文提出的方法实用、有效,可以达到高精度坐标转换的目的,在实际测量生产中具有一定的推广价值。

坐标转换;转换参数;空间直角坐标;稳健估计;IGGIII模型

0 引 言

在利用布尔萨七参数坐标转换模型进行三维空间直角坐标转换时,要通过所选择的公共点双重坐标解算两个坐标系之间的坐标转换参数,进而完成相应的坐标转换工作[1]。以往通常是利用经典最小二乘法解算坐标转换参数,但是根据现代平差理论,经典最小二乘法不具有抗干扰性,抵抗粗差的能力差[2],如果所选择使用的一个或多个公共点的精度较低或误差过大,那么将不可避免地影响所计算转换参数精度的高低,最终将整体影响所有待转换点的转换坐标的精度。但有时限于已知点数量的要求,个别坐标精度不高的已知点仍然需要使用,此时若根据最小二乘准则[3]解算坐标转换参数,会使解算结果精度降低,最终导致待转换点的转换坐标结果失真。因此,本文研究了稳健抗差估计理论,目的在于克服个别已知点坐标精度较低或误差过大对求解坐标转换参数带来的影响,探讨了一种高精度求解坐标转换参数的有效方法。

1 基于稳健估计理论的坐标转换算法

1.1经典最小二乘坐标转换算法

对于两个空间直角坐标系的坐标转换,存在着3个平移参数、3个旋转参数以及1个尺度变化参数,相应的坐标转换模型为[4]

(1)

令a1=m+1,a2=a1·εX,a3=a1·εY,a4=a1·εZ,则将式(1)改写为

(2)

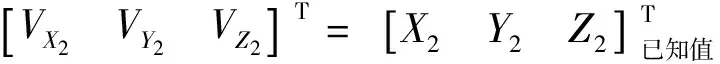
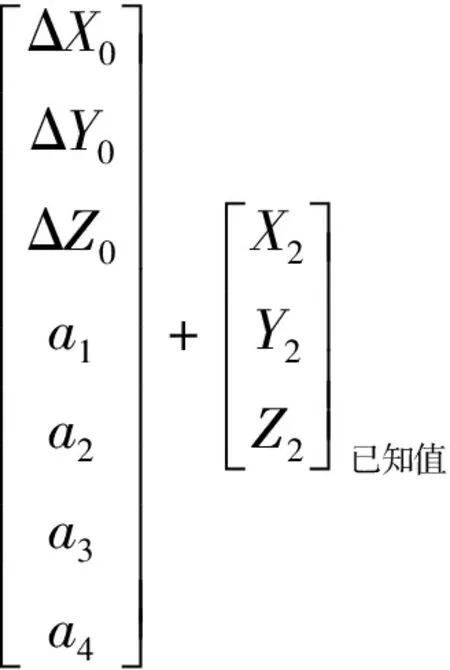
(3)

其矩阵形式为

V=B·ξX+L,

(4)

ξX=-(BTPB)-1BTPL.

(5)

由式(5)可进一步解算得到m=a1-1,εX=a2/a1,εY=a3/a1,εZ=a4/a1.

1.2结合IGGIII模型的抗差坐标转换算法

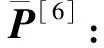
(6)

1.3抗差坐标转换迭代流程

1) 选取至少3个已知坐标的公共点,按照1.1节所述,通过经典最小二乘法解算坐标转换参数;

2) 将求解的坐标转换参数代入到布尔萨七参数坐标转换模型,对所选取的公共点进行坐标转换,与已知坐标进行比较,计算其差值,通过式(6)重新计算其权矩阵;

3) 重复步骤(2),直至计算得到的坐标差值小于所设置的阈值,阈值的选取和控制网的等级有关,在依次的解算中确定高精度坐标转换参数,利用最终得到的坐标转换参数对所有待转换点进行坐标转换。

2 算例分析

现将利用精密仪器及严密的测量手段布设得到的GPS首级控制网进行平差计算,得到某地区位于两个坐标系统下的4个高精度控制点的坐标,如表1所示。

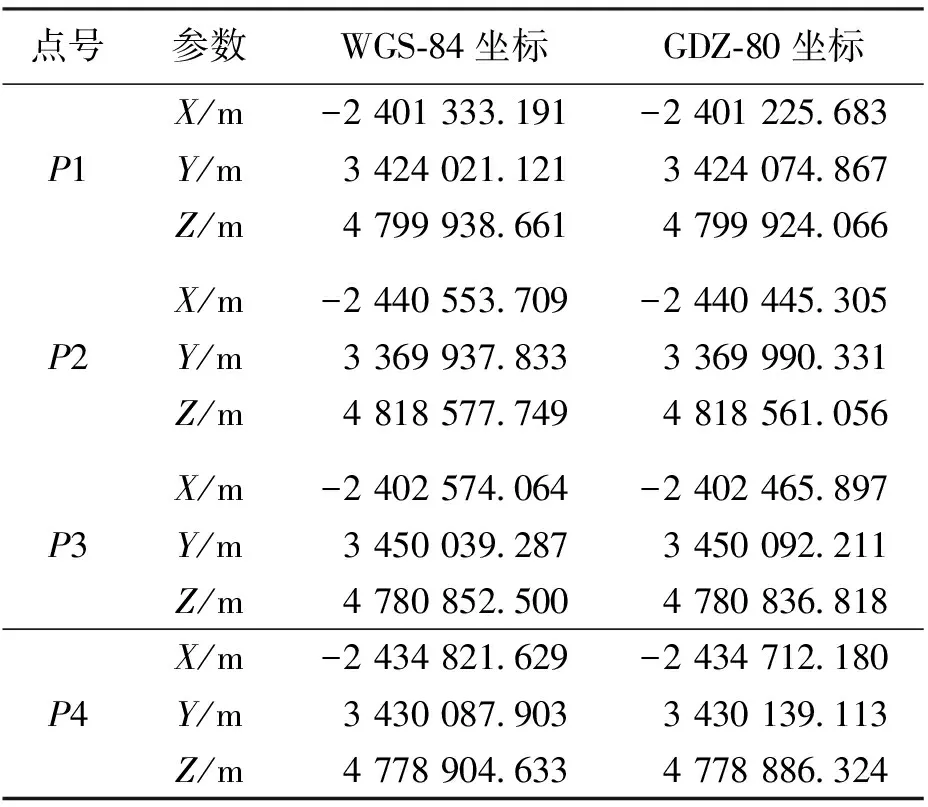
表1 已知点坐标信息

方案1: 选取p1、p2、p3、p4作为公共点,利用传统最小二乘法解算坐标转换参数,然后通过所求的坐标转换参数对点p1、p2、p3、p4的WGS-84坐标进行坐标转换,转换至GDZ-80坐标系统下,计算转换后的坐标与公共点原GDZ-80坐标的差值,记为|Δ1|。

方案2: 现将p1点的X、Y、Z坐标分别人为地加入4 cm、3 cm、2 cm的粗差(点位偏差约为5.4 cm),并保持其他各点坐标正确,然后利用p1、p2、p3、p4这四个公共点采用经典最小二乘法计算坐标转换参数。最后通过所求转换参数对点p1、p2、p3、p4的WGS-84坐标进行坐标转换,转换至GDZ-80坐标系统下,计算转换后的坐标与公共点原GDZ-80坐标的差值,记为|Δ1|,然后计算各点中误差m1。再利用含有粗差的p1点和p2、p3、p4公共点采用本文所述的抗差迭代坐标转换算法计算坐标转换参数(经计算一共迭代了3次),然后通过所求转换参数对点p1、p2、p3、p4的WGS-84坐标进行坐标转换,转换至GDZ-80坐标系统下,计算转换后的坐标与公共点原GDZ-80坐标的差值,记为|Δ2|,计算各点中误差m2.

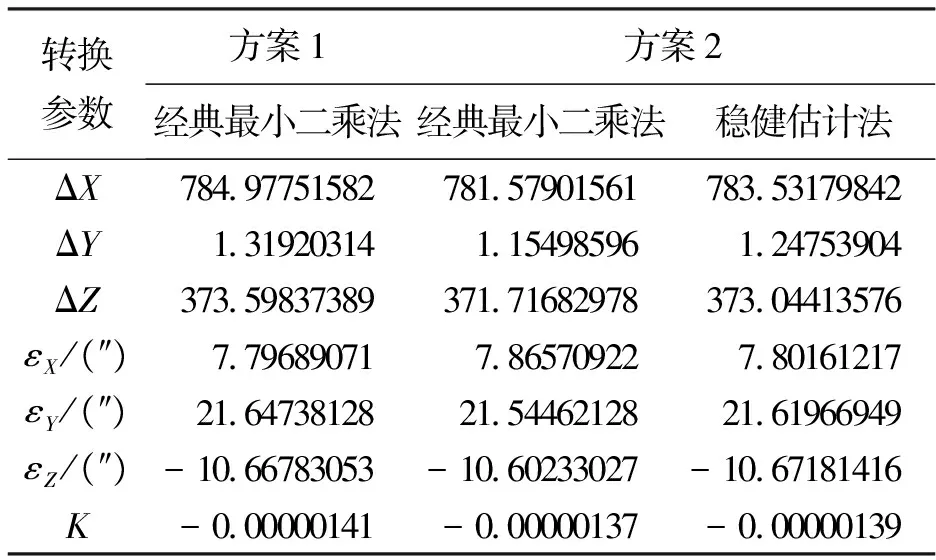
表2 两个方案坐标转换参数信息

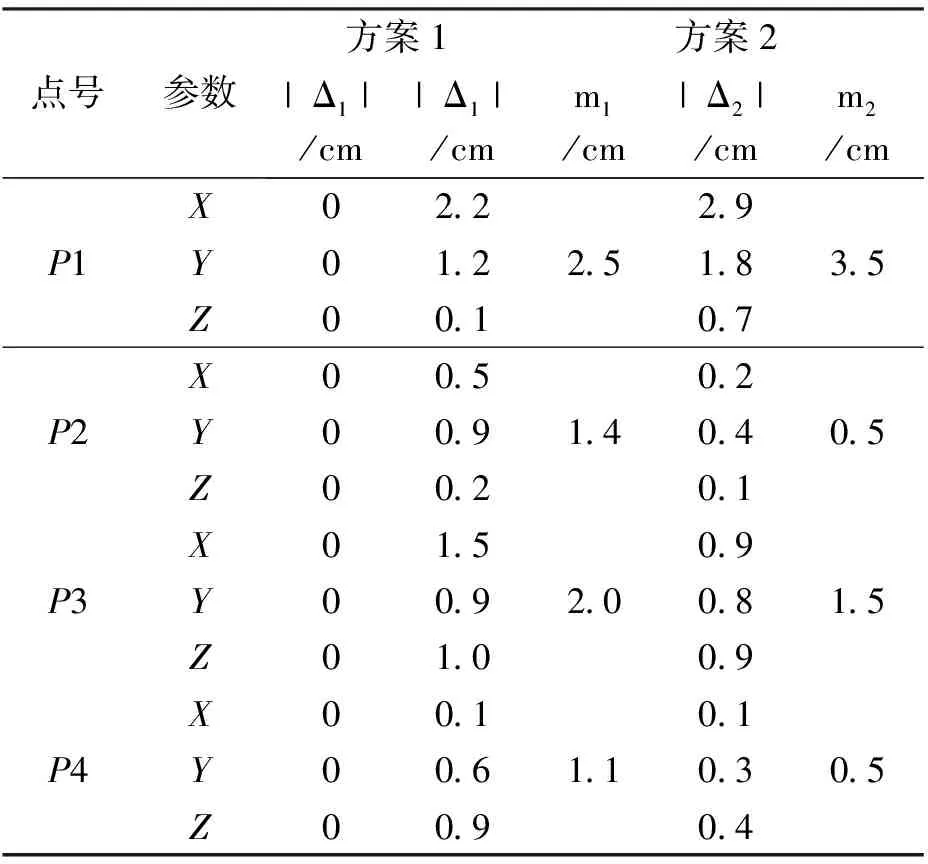
表3 各点转换后坐标差值及其精度

分析方案1: 由于公共点的精度非常高,所以转换后的坐标和已知坐标的差值均为0.

分析方案2: 可见由于p1点精度低、误差过大,所以各点坐标转换后的差值相较于方案1中的差值(全为0)全部增大,尤其是p1点转换后的坐标差值最大。综合分析表3中方案2的|Δ1|和|Δ2|、m1和m2,除了p1点外其它各点通过稳健估计原理进行坐标转换后的坐标的点位偏差都减小了。而对于点p1,虽然其点位偏差变大了,但其实它相对于利用经典最小二乘法计算的转换坐标更接近于真实值的。由此可见,将稳健抗差估计方法应用于坐标转换,是可行的、有效的,能够抵抗粗差。

3 结束语

本文将稳健抗差估计理论应用于三维空间直角坐标转换,介绍了基于IGGIII模型的抗差迭代坐标转换算法,采用C#语言进行了编程实现。通过对实际测量工程中的数据进行计算,分析表明当已知公共点中有一个公共点的坐标精度较低或误差过大时,本文提出的坐标转换方法可以有效的提高坐标转换的精度,在实际测量工作中是可行的。但是在工业安装测量、盾构机导向测量等许多实际测量中,经常会遇到旋转角为大旋转角的情况,如果仍简单套用已有的坐标转换模型,就可能得到错误的计算结果,因此,如何有效的提高旋转角为大旋转角情况下的坐标转换精度是作者接下来要研究和解决的问题。

[1] 刘大杰,施一民,过静珺. 全球定位系统(GPS)的原理与数据处理[M]. 上海:同济大学出版社,1999.

[2] 黄维彬. 近代平差理论及其应用[M]. 北京:八一出版社,1992.

[3] 崔希璋,於宗俦,陶本藻,等. 广义测量平差(新版)[M]. 武汉:武汉大学出版社,2009.

[4] 潘国荣,赵鹏飞. 基于空间向量的三维基准转换模型[J]. 大地测量与地球动力学,2009(6):79-82.

[5] 郭英起,唐彬,张秋江,等. 基于空间直角坐标系的高精度坐标转换方法研究[J]. 大地测量与地球动力学,2012(2):125-128.

[6] 邹进贵,李琴,王铜,等. Helmert方差分量估计理论的优化及其在形变监测网中的应用[J]. 武汉大学学报(信息科学版),2009,34(9):1076-1079.

[7] 刘长建,马高峰. 抗差Helmert方差分量估计及其应用[J]. 北京测绘,2002(1):16-21.

ResearchonResistanceCoordinateTransformationMethodofHighAccuracyBasedonIGGIIIModel

ZHANGYang1,ZHANGZhigang1,QIANDong1,HUANGYansong2,YULonghao3

(1.SuzhouGeologicalEngineeringInvestigationInstitute,Suzhou215129,China; 2.NanjingInstituteofSurveying,Mappingamp;GeotechnicalinvestigationStockCo.Ltd,Nanjing211100,China;3.CollegeofSurveyingandMappingEngineering,BeijingUniversityofCivilEngineeringandArchitecture,Beijing102616,China)

A high precision spatial coordinate transformation method based on the robust robustness estimation theory is proposed to avoid the influence of the coordinates of the common point coordinates or the error is too large to solve the coordinate transformation parameters. The method uses IGGIII model redefines the common point with low accuracy or large error, and gradually reduces its role in solving the coordinate transformation parameters, and obtains the reliable coordinate transformation parameters. Finally, the algorithm is used to calculate the common point coordinate data in a project instance. The comparison between the two schemes shows that the proposed method is practical and effective, and can achieve the goal of high precision coordinate transformation. In the actual measurement production has a certain value to promote.

Coordinate transformation; transformation parameters; cartesian coordinates; robust estimation; IGGIII model

10.13442/j.gnss.1008-9268.2017.05.005

P228.4

A

1008-9268(2017)05-0025-04

2017-04-21

江苏省地质矿产勘查局科研项目(编号：2016-KY-03)

联系人: 张洋E-mail: 873240839@qq.com

张洋(1968-),男,江苏徐州人,高级工程师,主要从事精密工程测量方面的研究。

张志刚(1971-),男,主要从事GPS测量与数据处理。

钱栋(1983-),男,主要从事轨道检测及变形测量。