小题大做
——一道向量小题的解法探究与教学反思
莫利琴 官 欣
(昆明一中,云南 昆明 650030;昆明市西山区粤秀中学,云南 昆明 650031)
小题大做
——一道向量小题的解法探究与教学反思
莫利琴 官 欣
(昆明一中,云南 昆明 650030;昆明市西山区粤秀中学,云南 昆明 650031)
通过一道向量小题的解法与错误分析,想到在数学具体内容教学和解题教学过程中的情景,提出学生在学习、考试中表现出的问题,其实是教师平时知识教学和解题教学中的问题.
平面向量;小题;解法;反思


命题解析本题以选择题的形式出现,是一道以三角形为背景的平面向量问题. 平面向量在高考中的考查通常是简单题到中档题,一般以选择题或填空题的形式出现(有时在解答题中和三角函数一起考查),常考三方面的内容:1.向量的坐标运算;2.平行四边形法则(三角形法则);3.一个向量在另一个向量上的投影问题.应该说考查内容、考察形式和难度基本都是相对固定的,属于必得分题.但本题学生普遍感觉比较困难,得分率很低.

解法、原理、错误分析

原理平面向量基本定理告诉我们:平面内的任一向量可以由这个平面内任意两个不共线的向量表示.选择好基底后,平面任一向量都可用这组基底来唯一表示.
错误原因思维定势,没有合理地选择基底.学生按照习惯选择以三角形的某一顶点引出的两条边所成的向量为基向量,而忽视了这两个向量的模和夹角都未知,从而无法求解.通常选基底的原则是这两个向量有尽量多的已知元素.
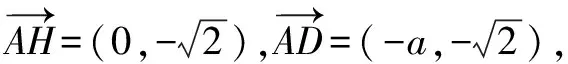
原理根据平面向量坐标运算法则:如果a=(x1,y1),b=(x2,y2),那么a·b=x1x2+y1y2.
错误原因对未知数(量)的恐惧 .学生们对于运算过程中的未知量总是觉得别扭,不敢主动设未知数,不敢带着未知数运算.

原理设θ为a与b的夹角,则acosθ叫做向量a在b方向上的投影
错误原因对向量投影的概念不熟,对直角三角形中的边角关系不敏感.
解法4 (特殊值法)由于题中△ABC没有限制条件,可以设为等腰直角三角形(A为直角顶点),建系,则其余各点坐标可得,计算即可.
原理从特殊到一般是高中数学主要思想方法之一,对于没有太多限制的题目,特殊点、特殊位置、特殊图形是我们找到答案的快速方法,尤其选择题填空题,省时省力,是得分利器.
错误原因对高中数学思想方法理解掌握不够,拿到题就做,没有养成“一慢,二想,三动手”的习惯,也没有归类总结题型、做法的习惯.
反思提高学生的数学思维能力和解题能力(包括运算能力),一直是我们高中数学教学中想达到的目标之一,但很多时候,往往教师一眼可以看穿,觉得容易的题目,学生却问题多多.反思自己的教学过程,觉得问题大半在日常教学上:模式化明显,人为痕迹重;重讲授,轻启发;重纵向练习,轻横向联系;往往围绕一个问题,一种题型,甚至于一种做法反复训练,学生机械训练,疲于奔命.往往满足于完成老师拿来的题目,到后来,连单纯的解题,也会陷入题海,落入“见树不见林”的境地,思路越练越窄.最后形成教师“凌绝顶”,学生却“只在此山中,云深不知处”.
1.对于数学内容教学的反思“要使学生感到自己是一个研究者、思考者,而不是消极的知识“掌握者””.我们的课堂教学应该让学生经历数学问题的发展过程,逐步体验和学会从直观感知到观察发现,从抽象概括到推理证明,再到反思和构建的学习过程.然而在实际的课堂教学中,有时为了赶进度,有时怀疑学生的能力,有时是对教学目的认识有偏差,甚至为了省时省事,不敢不愿放手让学生自己探究,往往直接告诉学生:知识是什么样的,怎样用,用时应注意什么,然后开始大量的训练,还觉得课堂比较高效. “将数学作为一个现成的产品来教,留给学生活动的唯一机会就是所谓的应用,其实就是做问题.这不可能包含真正的数学,强有力作问题的只是一种模仿的数学……长期以来所教的沉闷的模仿数学,不是有效的数学,而是无价值的数学.”在这样的教学模式下学生知识之间没有联系,对知识理解不系统,知识结构没有建立起来,所以凡出现在知识点交汇处出的题目,就觉得困难重重,是似而非,畏手畏脚,更不要说自己探究什么数学问题了.
2.对于解题教学反思
“解题是一种实践性的技能…我们是通过模仿和实践来学会任何一种实践性技能的…在学习解题时,你必须观察和模仿别人在解题时的做法,最后你通过解题学会了解题.
想要提高学生的解题能力的教师,必须逐渐地培养学生思维里对题目的兴趣,并且给他们足够的机会去模仿和实践.…当教师在课堂上解一个题目时,他应当对他的思路稍加渲染,而且向自己提出那些他在帮助学生时使用的同样一些问题.受益于这样的引导,学生最终将发现这些问题和建议的正确用法.而且通过这样去做,学生将学到一些比任何具体的数学知识更重要的东西.”这两段话很好地阐述了作为教师应该怎样进行解题教学.“模仿-实践-兴趣-思路引导”,学生在此题中出现的问题,是在以前的学习中,光有模仿和实践,没有关于解题思路的真正理解,由于疲于解题,忙于应付,更谈不上兴趣,所以实际操作中,题目条件、问法、表述方法稍有变化,就处理不了.想想课堂上,如果我们仅仅是让学生反复地练习而忽视对思路的分析、对解题原理的探讨、对涉及到的知识点的再加工,必然会导致学生的思想僵化,方法单一,失去做题的动力和兴趣.形成课堂上“学生皆醉,老师独醒”,考试时,老师觉得简单,学生感觉痛苦的局面.
学生表现出来的问题,是以往教学中问题的堆积,而通过学生表现出的问题,老师更应该反思自己的问题,从而不断提高,实现教学相长.
[1] 人民教育出版社,课程教材研究所,中学数学课程教材研究开发中心编著.普通高中课程标准实验教科书:数学必修[M].北京:人民教育出版社,2011.
[2] [苏]B.A.苏霍姆林斯基著.给教师的建议[M]杜殿坤编译.教育科学出版社1984年第二版,537.
[3] 弗赖登塔尔.作为教育任务的数学[M].陈昌平,唐瑞芬,李士锜,等,译.上海:上海教育出版社,1995.
[责任编辑:杨惠民]
2017-07-01
莫利琴(1974.11-),女,云南省昆明人,中学一级教师,从事高中数学教学.
官欣(1975.12-),男,云南省昆明人,中学一级教师,从事高中数学教学.
G632
A
1008-0333(2017)28-0032-02

