导数复习几点例谈
冯厚发
(南京市雨花台中学,江苏 南京 210000)
导数复习几点例谈
冯厚发
(南京市雨花台中学,江苏 南京 210000)
导数教学是函数教学的升华,运用导数知识可以将函数模型的研究上升到更高的层面,解决各种高次函数、复合函数等一系列复杂函数.如何运用导数解决相关问题,在复习中注重哪些知识层面,本文做一番简单的梳理.
导数;函数;基础;单调性;最值;分类;多元降解
有了导数,中学数学对于函数的学习向前大大推进了一大步.以往的初等基本函数可以各式各样的进行整合,对于学生理解函数、解决函数问题有了更广阔的空间.导数的基本知识并不是太复杂,如何利用好这些基本知识以及所涉及到的其他相关数学思想,才是导数复习最为关注的地方.本文结合基本的知识使用,利用一定的知识层面、数学思想方法,将导数复习做一番合理的梳理,力争让导数知识在解决函数问题时更为有效.
一、注重几何意义
导数最基本的几何意义是切线的斜率,对于基本知识的理解需要从几何意义出发.
问题1 若曲线y=x4的一条切线l与直线x+4y-8=0垂直,则l的方程为________.
分析导数的几何意义是在该点处切线的斜率,中学数学教材对此有明确的推导和证明,要掌握和理解几何意义是问题解决的最基本保障.与直线x+4y-8=0垂直的直线l为4x-y+m=0,即y=x4在某一点的导数为4,而y′=4x3,所以y=x4在(1,1)处导数为4,此点的切线为4x-y-3=0.
二、注重单调最值
导数的作用在于方便地解决了函数单调性,与定义研究单调性不同的是,导数站在更高的系统的角度思考了函数的变化,进而方便地获得了函数的最值.
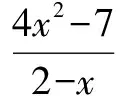


x00,1/2()1/21/2,1()1f′(x)-0+f(x)-7/2↘-4↗-3
三、注重分类讨论
对于定值研究,学生并没有特别的困难,但是对于变量的引入,往往产生了大量的讨论,这也是很多学生开始陷入导数复习困扰的地方.学会变量的如何介入讨论,是导数复习的关键.
1.二次项系数的切入
问题3 已知函数f(x)=plnx+(p-1)x2+1,当p>0时,讨论函数f(x)的单调性.

显然,本题的讨论主要是从二次项系数出发的,与二次函数讨论一致,二次项系数是突破本题的关键.
2.对称轴引发的思考

分析由已知得g(x)=ln(x+1)+3-(-2x2+4ax+3)=ln(x+1)+2x2-4ax,

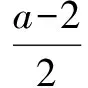
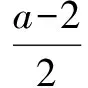
综上,实数a的取值范围是a≤0.
对于导函数来说,二次项系数为定值时,一次项系数为变量,从而从这里介入讨论是最为合适的.
四、注重多元降解
导数考查的更高层次是多元变量的介入,当遇到多元变量时,我们如何利用导数解决问题?从思想角度来说,笔者将其称之为多元变量讲解,即多元转少元.
问题5 函数f(x)=alnx+x2+bx存在极大值.(1)若a=1,求b的取值范围;(2)求a的最大值,对满足题意的所有的b而言,函数f(x)的极大值恒小于0.

总之,导数是一种工具性的知识,和向量知识一样,其解决初等数学问题的时候,大大向前推进了一大步,这是我们学习导数的主要目的.复习导数最为关键的是依赖其本质出发,本文阐述的前两个方面就是点出了这两点,即如何思考运用几何意义和单调性最值的解决,是导数最基本的工具性作用;进一步运用导数是借助其工具性作用和思想方法的结合,笔者认为比较重要的是分类讨论思想和多元降解方式的处理,这是导数复习问题中较难掌控的因此值得复习教学多加以关注.
[1]柴贤亭.数学教学中的导数问题设计[J].数学教学研究,2015(10).
[2]鲍建生等.导数变式教学研究[J].数学教学,2013(1).
[责任编辑:杨惠民]
2017-07-01
冯厚发(1971.04-),男,江苏南京人,大学本科,从事数学教学.
G632
A
1008-0333(2017)28-0005-02

