小议数形结合求最值

骆纤雨

(华中师范大学附属中学高二(9)班，湖北 武汉 430000)

小议数形结合求最值

骆纤雨

(华中师范大学附属中学高二(9)班，湖北 武汉 430000)

本文论述了通过直线的斜率、截距、距离以及函数的增减性求函数的最值，并在此基础上通过数形结合让其更形象、更直观，进一步丰富数学数形结合的运用.

数形结合；最值

在数学问题的解决中，等价转化与数型结合思想有着极其重要的应用，尤其在一定条件下，求某些式子的最值问题，就可利用数形结合的方法，转化为求斜率、截距、距离等问题，从而使问题得到解决.

数形结合的思想在数学计算最值中有大量的应用，特别是在二次函数、三角函数等中求最值最为方便快捷，直观性性也比较强，但是，数形结合求最值的最大难点是在如何把这些函数转变成与几何图形相结合的等价变换，这不仅是个难点，还是重点.下面笔者简要地对利用直线的斜率、截距、距离求最值进行了解题分析与例举，希望读者有所收获.

一、转化为直线的斜率求最值

例1 如图1，若实数x、y满足(x-2)2+y2=3，求y/x的最大值及最小值.

点拨点(2，0)满足圆的方程，而y/x正是圆上的点与原点连线的斜率如果把(x,y)视为动点，借助图形观察，则y/x的最大值和最小值正是由原点向圆所引的两条切线的斜率.

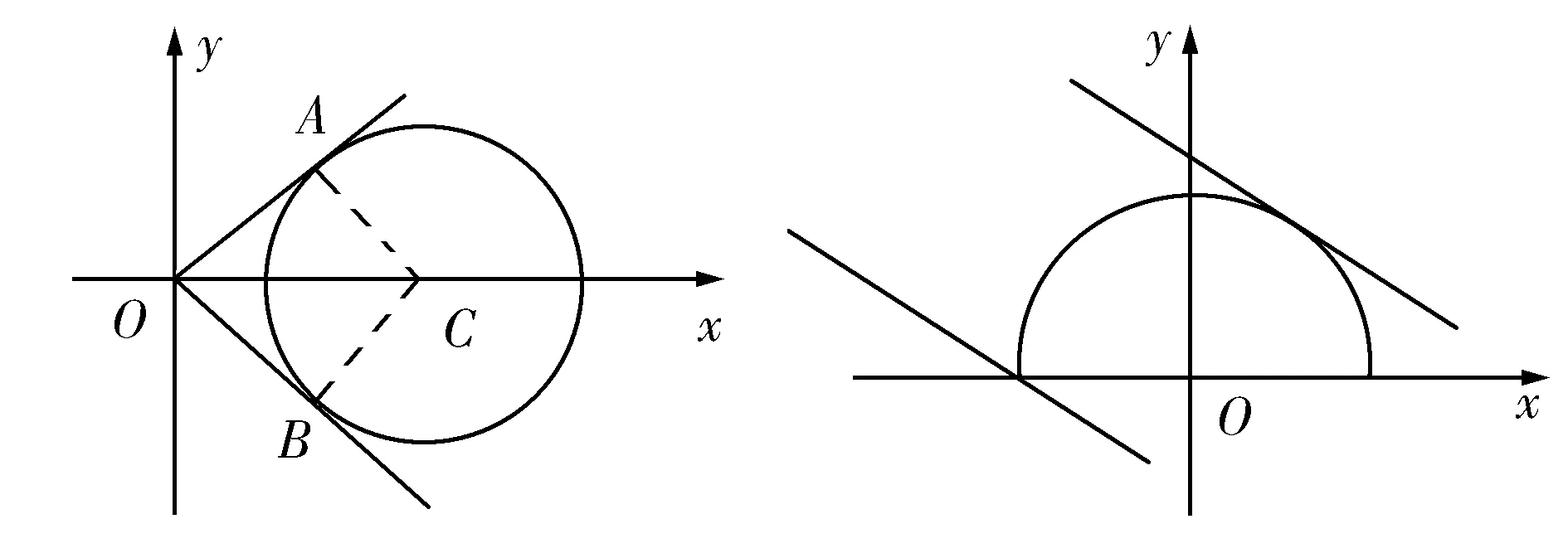
图1 图2

例题演练如实数x，y满足(x-2)2+y2=2.89，求y/x的最大值及最小值.方法如上.

二、转化为直线的截距求最值

例2 已知实数x，y满足x2+y2=1(y≥0)，求2x+y的取值范围.

点拨x2+y2=1(y≥0)是以原点为圆心位于x轴上半部分的一个半圆，设b=2x+y，问题就可以转化为直线与半圆的关系.

例题演练如实数x，y满足x2+y2=2.89(y≥0)，求4x+y的最大值及最小值.方法如上.

三、转化为距离求最值

例3 已知x，y满足x2+y2+4x-2y-4=0，求x2+y2的最大值.

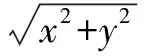
数形结合求最值，直观方便，但注意转换的时候必须是等价转换，自变量以及值域的范围既不能缩小也不能扩大，否则，就会引起不等价转换，会导致解题错误.

四、利用函数的增减性求最值

利用函数的增减性求最值，假如函数y=ax+b是增函数，那么在区间[c，d]上的最大值为x=d时y的值，最小值为x=c时y的值；假如函数y=ax+b是减函数，那么在区间[c，d]上的最大值为x=c时y的值，最小值为x=d时y的值.

例4 求y=6x+7在区间[-1，10]上的最大值与最小值.

解由于y=6x+7在区间[-1，10]为增函数，当x=-1时，y的最小为1；当x=10时，y的最大值为67.

例5 求y=-6x+7在区间[-1，10]上的最大值与最小值.

解由于y=-6x+7在区间[-1，10]为减函数，当x=-1时，y的最大为13；当x=10时，y的最大值为-53.

例题演练1.求y=5x+7在区间[1，9]的最大值与最小值.

五、利用函数图象的顶点与增减性求最大值与最小值

如果二次函数y=ax2+bx+c(a≠0)的图象开口朝上，那么顶点就是其最小值，如开口朝下，那么顶点就是其最大值，如求最值的区间不包括顶点，只是在函数图象的一侧，这时可以运用增减性 ，求最值.

例题演练1.求函数y=2x2+6x+4在区间[1，5]的最大值与最小值.

[1]南开大学数学系.空间解析几何引论[M].北京:人民教育出版社，1978.

[2]林崇德等.林崇德《学习与发展》观介绍[N].中国教育报，1991(03)：31.

[3]袁桂珍等.高中数学解题方法与能力训练[M].桂林:广西师范大学出版社,1996:29.

[责任编辑：杨惠民]

2017-07-01

骆纤雨(2000.05-)，浙江省，华中师范大学第一附属中学，高中在读.

G632

A

1008-0333(2017)28-0014-02