基于改进蚁群算法的行驶工况构建及精度分析

刘炳姣, 石 琴, 仇多洋, 陈一锴

(1.合肥工业大学 汽车与交通工程学院,安徽 合肥 230009; 2.合肥工业大学 机械工程学院,安徽 合肥 230009)

基于改进蚁群算法的行驶工况构建及精度分析

刘炳姣1, 石 琴1, 仇多洋2, 陈一锴1

(1.合肥工业大学 汽车与交通工程学院,安徽 合肥 230009; 2.合肥工业大学 机械工程学院,安徽 合肥 230009)

文章以合肥市典型道路为例,选取5条城市道路进行数据采集,采用主成分分析与遗传变异改进的蚁群算法(ant colony optimization,ACO)相结合的方法,构建了合肥市典型行驶工况。在划分了运动学片段的基础上,利用主成分分析法对13个运动学特征参数进行降维处理,以排名前3的主成分为聚类因子,用改进的蚁群算法对运动学片段样本进行分类,通过组合类内运动学片段,完成代表性工况的构建,并对代表性工况进行精度分析。研究结果表明,与K-means聚类法、系统聚类法相比,改进的ACO能够有效提高行驶工况的构建精度。

主成分分析;遗传变异;蚁群算法(ACO);行驶工况(DC)

0 引 言

随着科技的迅速发展,能源短缺和环境污染问题日益严重,节能减排已成为全世界的重大课题。汽车行驶工况(driving cycle,DC)是针对某一类型车辆在特定交通环境下用以描述车辆行驶特征的速度-时间曲线。它被用于评估车辆的污染物排放和燃油消耗状况、新车型的技术开发等。

最近数十年,美国、欧洲、日本等国家和地区已根据其相应的车辆及交通状况构建出各自的行驶工况。文献[1]研究了马尔可夫法在工况构建中的应用;文献[2]用K-means聚类法构建了德黑兰的行驶工况。近年来,国内学者在DC开发与构建方面也做了一些研究,文献[3]研究了改进的短行程法在城市公交行驶工况中的应用;文献[4]利用两阶段聚类法对西安市环卫车的行驶工况进行了研究;文献[5]通过分析车辆速度及能耗状态,构建了济南市的行驶工况。

目前,构建行驶工况过程中使用最广泛的是主成分分析和聚类分析相结合的方法,但因传统聚类算法或对初始值过于敏感,或易陷入局部最优解,导致工况的构建精度过低。因此,本文对传统蚁群算法(ant colony optimization,ACO)进行了改进,并以合肥市典型道路为例,利用主成分分析法与改进的ACO构建行驶工况,与常用的K-means算法和系统聚类法进行了精度对比,验证了本文提出方法的有效性。

1 理论基础

1.1 研究方法

主成分分析是数据降维的多元统计学方法,主要思想是通过对原始运动学片段的分析,提取少数几个能综合反映大部分特征参数信息的主成分,从而达到简化数据的目的。聚类分析则用于反映不同类型片段的运动学特征[6]。

常见的聚类方法有K-means聚类法、系统聚类法、模糊聚类法、动态聚类法等。K-means算法容易陷入局部最优解,对唯一参数K值的选择没有固定规律可参考[7]。系统聚类法则难以确定结果类的数目,在聚类过程中产生的合并项和分裂项都无法回复,对结果有较大影响。而传统的模糊聚类法对孤立点数据十分敏感,且因为其用迭代爬山式算法,所以易陷入局部极值点,得不到最优解[8]。

ACO 则是一种用来寻找优化路径的机率型算法,但基本ACO在搜索过程中容易出现停滞现象,不利于发现更优解。若在ACO中引入遗传算法中的变异因子,则可以很好地解决这一问题。

相比于其他算法,遗传变异改进的ACO有如下优点:能够在智能搜索的同时进行全局优化;有较强的稳健性和鲁棒性,不会出现停滞现象;数据个体间不断进行信息交换与传递,易于寻找更优解。

鉴于以上几点,本文将主成分分析与遗传变异的ACO相结合,用以构建行驶工况。

1.2 基本ACO

为解释遗传变异的ACO,首先需引入基本ACO的概念[9],简述如下。

设N={1,2,…,n}为n个地点的集合,A={(i,j)|i,j∈N}为N中元素两两连接的集合,bi(t)表示t时刻位于地点i的蚂蚁数,假设m只蚂蚁都随机选择一个地点作为其出发地点,则有:

(1)

蚂蚁在构建路径的每一步中,按照随机比例选择下个要到达的地点,即

(2)

其中,i,j分别为起点和终点;τij(t)为时间t由i到j的信息素浓度;ηij=1/dij为能见度,是i,j两点间距的倒数;allowedk为尚未访问过的节点集合;α、β为常数,代表信息素和能见度的加权值。

每只蚂蚁完成一次循环后,都会在其访问过的路径上留下相应信息素。

当所有蚂蚁完成一次循环后,各路径的信息素随之更新,即

τij(t+n)=ρτij(t)+Δτij

(3)

(4)

其中,ρ(0<ρ<1)为信息残留度;Δτij为迭代中边ij的信息素增量。

ACO不断地通过上述过程构建路径和更新信息素,最终得以寻找到最优解。

1.3 遗传变异改进的ACO

ACO作为一种本质并行的正反馈算法,个体间不断进行信息传递和交流,易发现最优解。但基本ACO有一些缺陷,如搜索时间较长,很难在短时间内找到较好的路径;当样本数据量较大时会陷入局部最优解,过早收敛。

为解决这些问题,本文引入遗传算法中变异率对基本ACO进行改进。具体方法如下:加入变异率p,并在所得最佳路径内局部寻优;同时产生一个随机数组,若数组中某值小于变异率p,则随机改变其对应的路径标记;随后计算各样本数据点到其相应的临时聚类中心的最小欧式距离之和F′及本次迭代的最佳路径,更新信息素,循环此过程直至寻找到最优解。

遗传变异改进的ACO流程如图1所示。

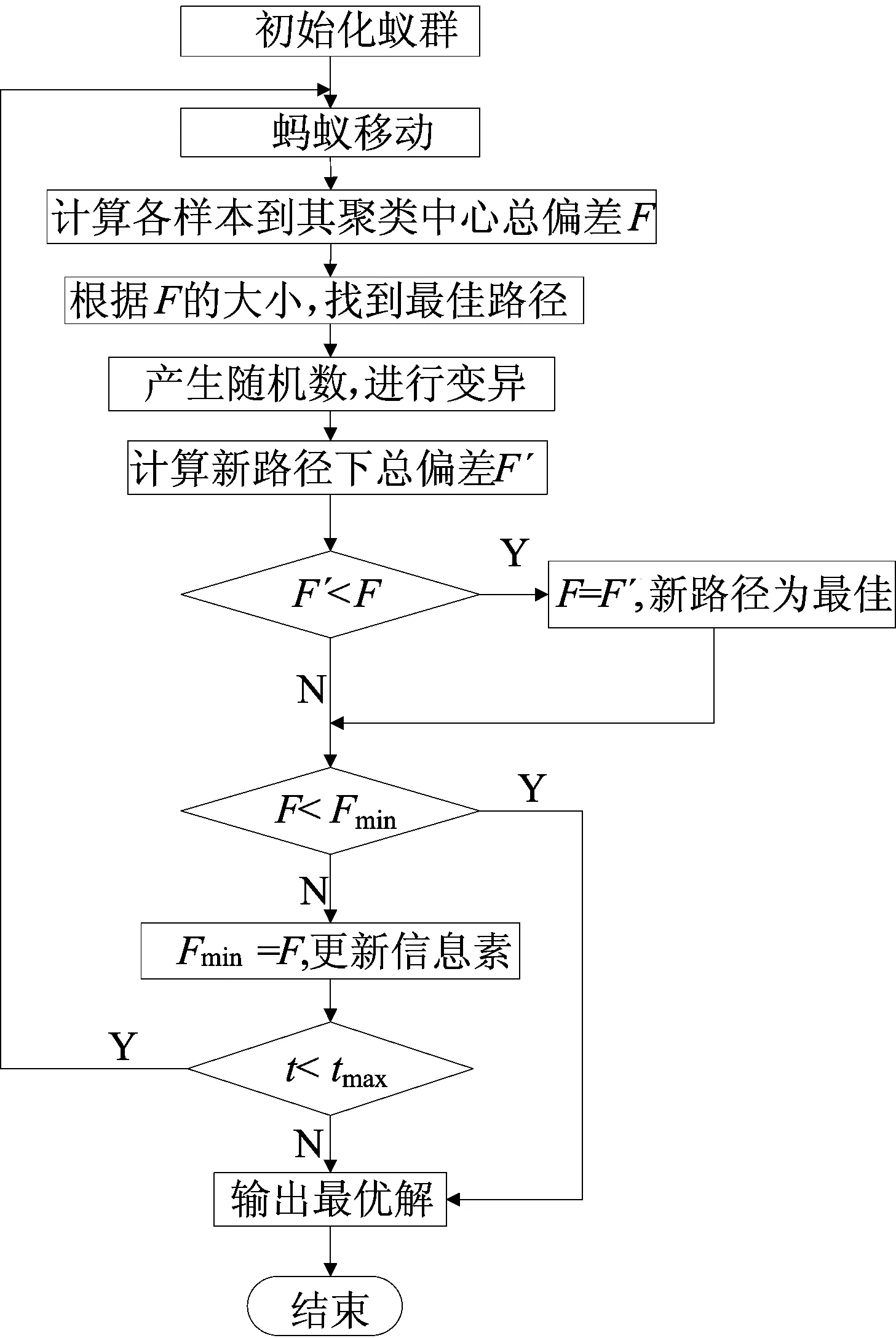
图1 遗传变异改进的ACO流程

2 试验数据获取与预处理

2.1 试验与数据采集

为反映城市典型道路的车辆行驶工况,综合考虑道路类型、车流密度、交叉口密度等因素,本文以合肥市区道路为例,选取5条(主干道的徽州大道、胜利路、明光路,次干道的桐城路,快速路的屯溪路)代表性的城市道路进行试验及数据采集。

考虑时间因素对工况的影响,本次试验采样时间定为上午7:00—9:00,下午13:00—15:00、16:30—18:30,包括每天的早、晚高峰期及平峰期,持续4 d,含工作日及非工作日。试验中某次行驶过程获取的工况数据如图2所示。

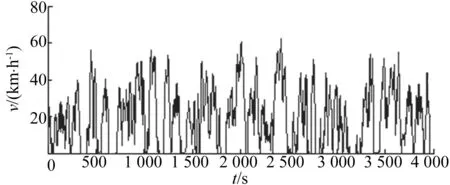
图2 实测工况数据

试验采用平均车流统计法,即驾驶员驾驶试验车,在选定的时间和道路上随平均车流行驶。数据使用OES-Ⅱ非接触式光电速度传感器采集,采集频率为1 Hz,可获得速度、加速度、路程以及时间等参数,最终得到4万余组数据。

从图2数据可以看出,车辆在行驶过程中会频繁加速、减速、停车、启动,为方便描述该过程,本文将整个行驶历程划分为多个数据单元,在此需引入运动学片段的概念。

2.2 运动学片段的划分

一个运动学片段是指在速度时间变化曲线上,从上一个怠速状态开始到下一个怠速状态结束之间的运动学单元,如图3所示。

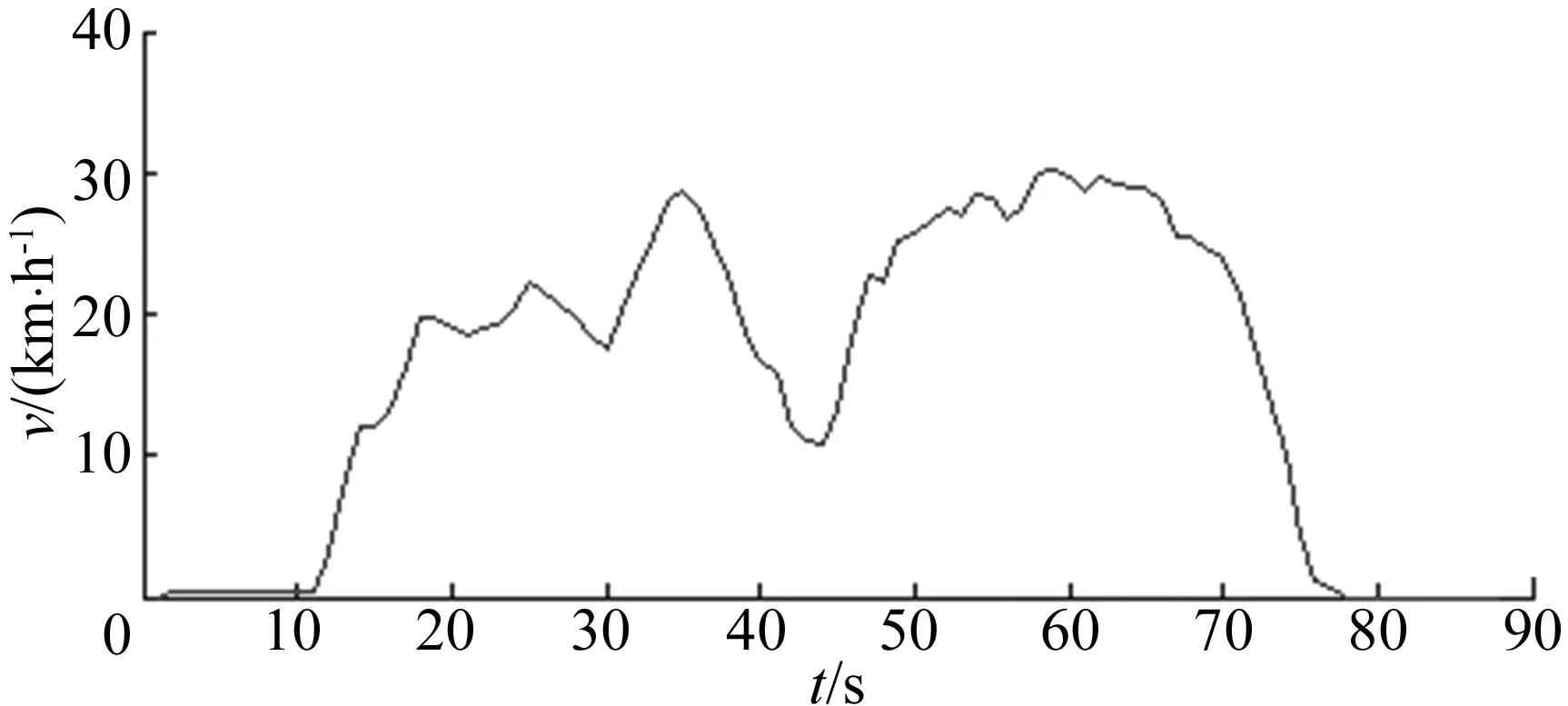
图3 运动学片段

参考国内外文献,将试验中采集到的数据按照以下原则进行运动学状态定义。

(1) 匀速状态。|a|<0.15 m/s2且v≠0的发动机连续工作状态。

(2) 怠速状态。a=0且v=0的发动机连续工作状态。

(3) 加速状态。a≥0.15 m/s2且v≠0的发动机连续工作状态。

(4) 减速状态。a≤-0.15 m/s2且v≠0的发动机连续工作状态

以此为划分规则,利用Matlab编程,对原始数据进行预处理,筛选得到126个有效的运动学片段。

2.3 运动学特征参数及参数矩阵

为准确描述各运动学片段,表征所用参数不可过少,否则会导致大量信息丢失;但参数过多,则会给分析过程增加不必要的难度和计算量。参考文献[10-12]对运动学参数的选取,本文选取了加速比例Pa、减速比例Pd、匀速比例Pc、怠速比例Pi等13个能够反映运动学片段特征的参数,以合理描述运动学片段。各运动学特征参数见表1所列。

以预处理阶段得到的126个运动学片段及其特征参数为研究对象,得到样本数×特征参数值的矩阵,见表2所列。

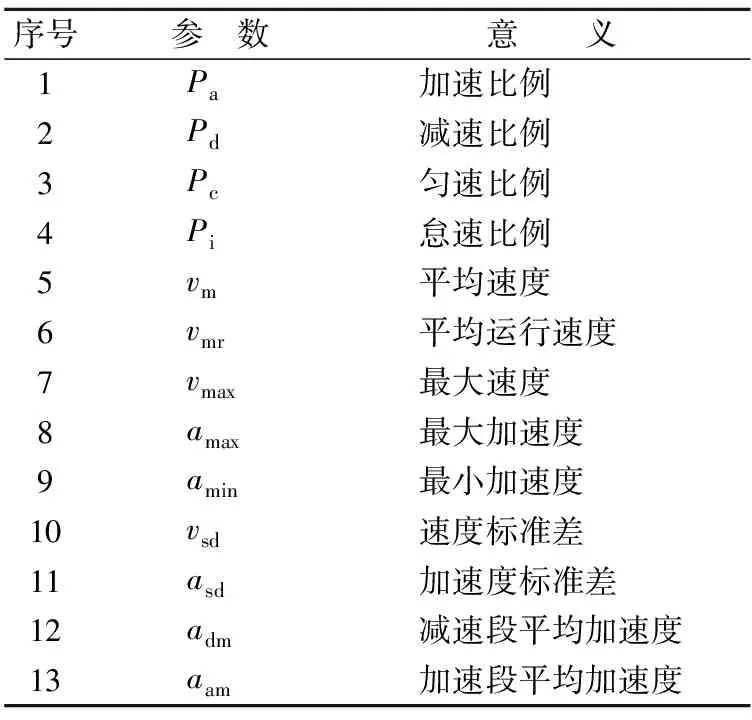
表1 运动学特征参数

注：平均运行速度指除怠速外的平均速度。

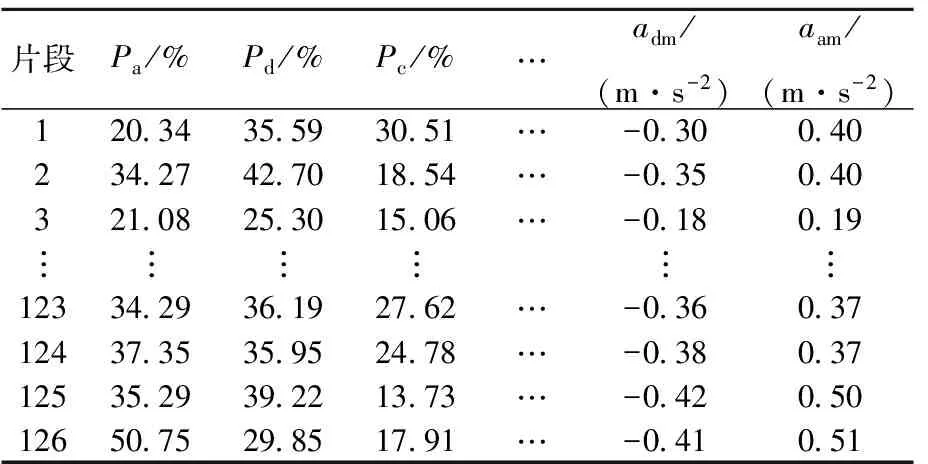
表2 运动学片段及其特征参数

2.4 主成分分析

主成分分析是利用降维思想,将多个参数转换为少数综合参数(即主成分)的过程。其中各主成分间没有相关性,且都是原始参数的线性组合,从而不重叠地反映原始参数的大部分信息,以达到简化问题的目的。

用SPSS软件对126个运动学片段及其特征参数进行主成分分析,得到各主成分(用Mi表示,i=1,2,3,…,13)特征值的方差贡献率及累计贡献率,见表3所列。

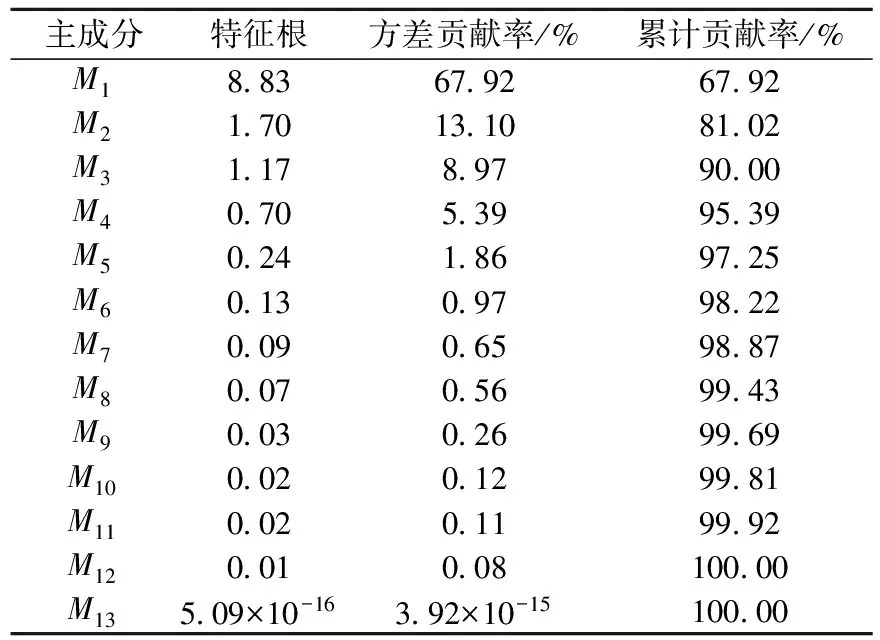
表3 各主成分贡献率

特征根是主成分影响力度的指标,代表引入该主成分后可解释的原始变量的信息量。若特征根大于1,说明该主成分的解释力度大于原变量的平均解释力度,因此一般将特征根大于1、累计贡献率大于85%作为主成分的纳入标准。由表3可以看出,前3个主成分的特征根均大于1,且方差的累计贡献率达到了90%,已足够描述运动学片段的特征,因此本文选取排名前3的主成分进行分析。主成分表达式为:

Fi=ai1X1+ai2X2+…+aijXj

(5)

其中,Fi为第i主成分;Xj为标准化后的第j个特征参数;aij为第i主成分对应的第j个特征参数的系数。由(5)式可得前3个主成分的数值。

3 行驶工况的构建与验证

3.1 聚类分析及结果

根据数据的交通特征,将运动学片段分为低速(多怠速、短运动学片段)、中速(加减速频繁、片段长度适中)和高速(少怠速、长运动学片段)3类。对排名前3的主成分数值进行遗传变异改进的蚁群聚类分析,并与常用的K-means聚类法及系统聚类法进行对比。遗传变异改进的ACO聚类结果如图4所示,K-means聚类结果和系统聚类部分结果分别见表4、表5所列。

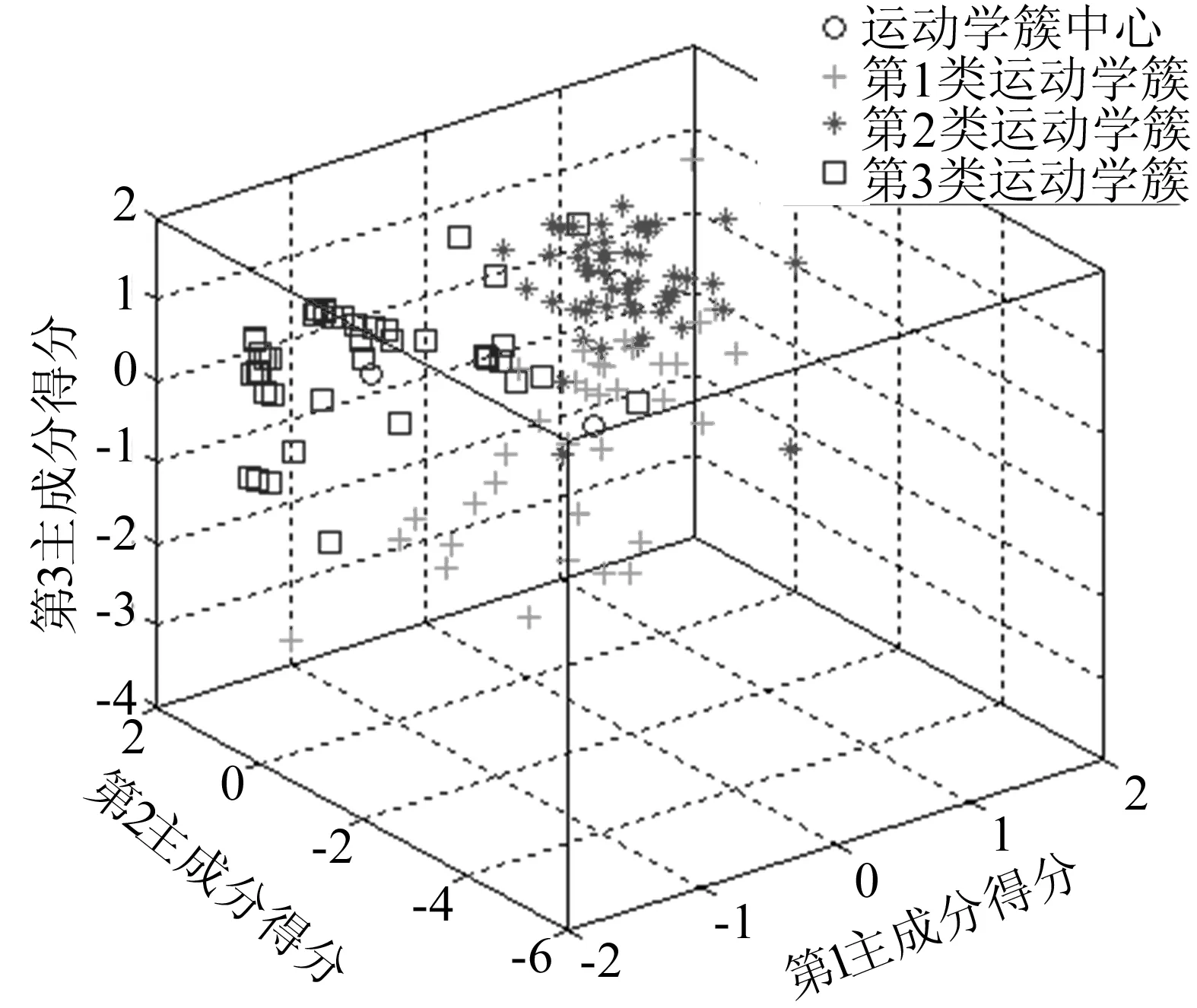
图4 遗传变异改进的ACO聚类结果

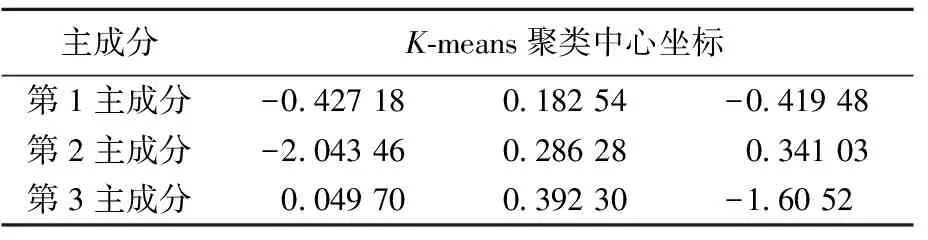
表4 K-means聚类结果

表5 系统聚类部分结果

由图4可以看出,用改进的ACO进行聚类,结果中第1类包括33个运动学片段,第2类包括55个运动学片段,第3类包括38个运动学片段。表4显示了K-means聚类法得到的前3个主成分聚类中心坐标;表5则展示了系统聚类法部分运动学片段的聚类结果。

3.2 建立代表性工况

将各类运动学片段分别进行组合,形成3种运动学片段簇。代表性工况一般为1 200 s左右,按各类所占总时间长度比及每个运动学片段与其所属运动学簇之间相关系数的大小,从改进的ACO聚类法形成的第1簇中选取片段110,第2簇中选取片段36、78、98,第3簇中选取片段29,拟合为代表性工况1。按照同样的选取规则,在K-means聚类法第1类的17个运动片段中选取片段47,第2类的73个运动片段中选取片段78、98、32,第3类的36个运动片段中选取片段35、114拟合为代表性工况2。同理,在系统聚类法第1类的72个运动片段中选取片段98、78、36,第2类的36个运动片段中选取片段67、95、119,第3类的18个运动片段中选取片段110,拟合为代表性工况3。

因数据变化幅度较大,拟合工况会产生“毛刺”现象,本文用五点三次平滑法对不规则抖动的速度时间曲线进行滤波处理,以减少对代表性工况的影响,形成的最终工况如图5所示。

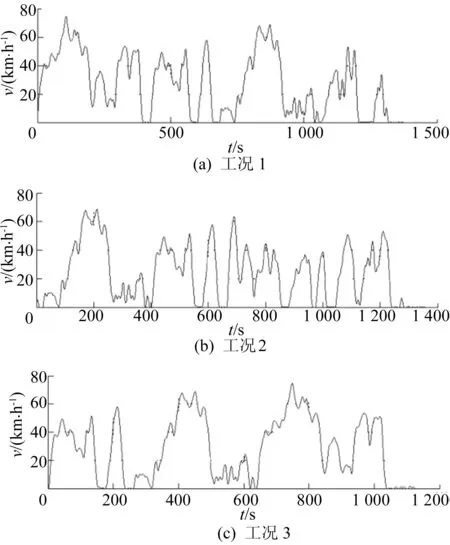
图5 3种拟合工况

3.3 基于特征参数的精度检验

为检验遗传变异改进的ACO聚类法在行驶工况中应用的精度,给出3种方法拟合工况与试验工况的相对误差,见表6所列。

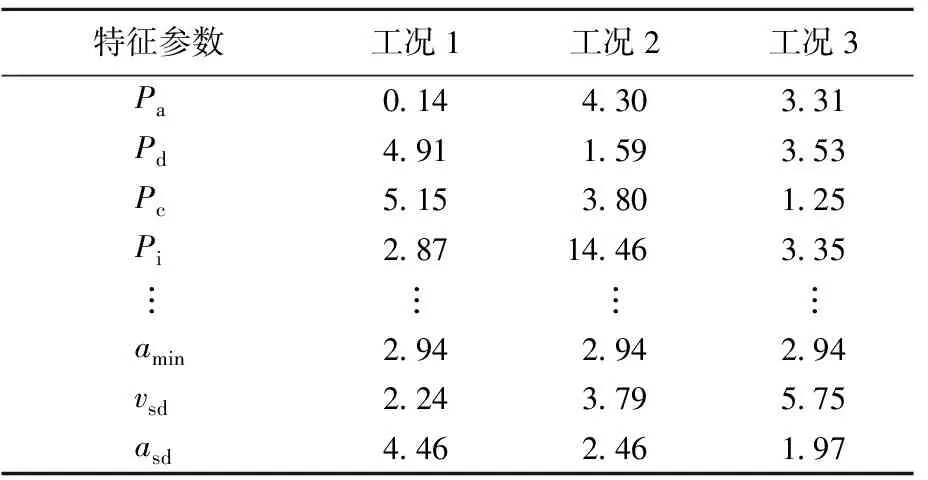
表6 3种拟合工况与试验工况特征参数的相对误差 %

本文引入平均误差,以期全面考察所建工况的精度。平均误差为:

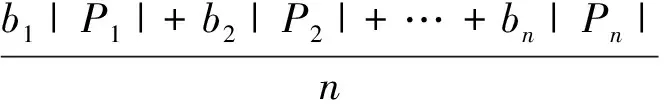
(6)

其中,bn为各参数的权重;Pn为各参数的相对误差。为简化计算,本文定义所有权重均为1。由表6数据可计算得到工况1、工况2、工况3的平均误差分别为3.64%、5.49%、4.51%。

由表6可以看出,以改进的ACO聚类法建立的拟合工况与试验工况的相对误差均在10%以内,且平均相对误差仅为3.64%,精度明显高于K-means均值聚类法及系统聚类法,说明了改进ACO在构建行驶工况中的优越性与有效性。

3.4 基于VA联合分布的误差分析

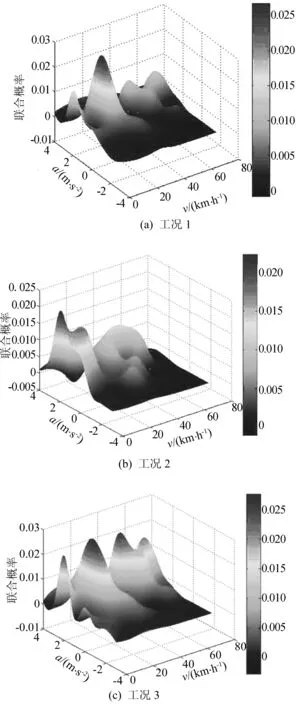
利用Matlab软件计算3种拟合工况的速度-加速度(velocity-acceleration,VA)联合分布平均误差,结果见表7所列。绘制拟合工况与原始数据的VA联合分布误差图,如图6所示,以便更直观地比较本文方法拟合的工况与原始数据的差异。

由表7可知,以改进ACO拟合的工况1的VA联合分布误差的平均值仅为0.26%,小于拟合工况2、工况3,这说明拟合工况1与试验工况有极高的相似度,优于工况2与工况3。

由图6可以看出,工况1与原始数据误差较大的区域仅集中于0

表7 拟合工况VA联合分布平均误差

图6 3种工况的VA联合分布误差

4 结 论

(1) 本文引入加速比例、减速比例、匀速比例、怠速比例、平均速度、平均运行速度、最大速度、最大加速度、最小加速度、速度标准差、加速度标准差、减速段平均加速度以及加速段平均加速度13个能够反映合肥市典型道路与交通状况的参数,用以描述工况特性。

(2) 通过主成分分析法对13个特征参数进行分析处理,提取出前3个主成分,并对其得分进行聚类分析,选取合适的运动学片段构建代表性工况。将改进ACO拟合的工况与K-means法、系统聚类法拟合的工况进行比较,结果表明,改进的ACO聚类精度更高。

(3) 以改进的ACO构建的代表性工况与原始数据相比,误差小于4%,可以综合反映合肥市实际道路交通状况,这为行驶工况的构建提供了新的研究方法。但ACO作为一种近年来兴起的模拟进化算法,仍有需要改进之处,如数据量大时,搜索时间较长。

[1] GONG Q,MIDLAM-MOHLWER S,MARANO V,et al.An iterative markov chain approach for generating vehicle driving cycles[J].SAE International Journal of Engines,2011(1):1035-1045.

[2] FOTOUHI A,MONTAZERI-GH M.Tehran driving cycle development using thek-means clustering method[J].Scientia Iranica,2013,20(2):286-293.

[3] 孙宏图,宋希庚,王天灵.改进的城市公交循环工况开发方法[J].大连理工大学学报,2009,49(6):837-841.

[4] 孙强,白书战,韩尔樑,等.基于试验测量的瞬时行驶工况构建[J].吉林大学学报(工学版),2015,45(2):364-370.

[5] 黄万友,程勇,李闯.基于车辆能耗状态的济南市道路行驶工况构建[J].西南交通大学学报,2013,47(6):989-995.

[6] 朱星宇,陈永强.SPSS多元统计分析方法及应用[M].北京:清华大学出版社,2011:241-248.

[7] 周大镯,姜文波,李敏强.一个高效的多变量时间序列聚类算法[J].计算机工程与应用,2010,46(1):137-139.

[8] 严骏.模糊聚类算法应用研究[D].杭州:浙江大学,2006.

[9] 杨剑峰.蚁群算法及其应用研究[D].杭州:浙江大学,2007.

[10] 李友文,石琴,姜平.基于马尔科夫过程的行驶工况构建中数据处理与分析[J].合肥工业大学学报(自然科学版),2010,33(4):491-494.

[11] ERICSSON E.Independent driving pattern factors and their influence on fuel-use and exhaust emission factors[J].Transportation Research Part D:Transport and Environment,2001,6(5):325-345.

[12] 艾国和,乔维高,李孟良,等.车辆行驶运动学参数构成分析[J].公路交通科技,2006,23(2):154-157.

Drivingcycleconstructionbasedonimprovedantcolonyoptimizationalgorithmandprecisionanalysis

LIU Bingjiao1, SHI Qin1, QIU Duoyang2, CHEN Yikai1

(1.School of Automobile and Traffic Engineering, Hefei University of Technology, Hefei 230009, China; 2.School of Mechanical Engineering, Hefei University of Technology, Hefei 230009, China)

Taking the measure data of five typical urban roads in Hefei City as an example, typical driving cycle(DC) of Hefei City is constructed with the method of principal component analysis and genetic variation improved ant colony optimization(ACO) algorithm. Based on the definition of the kinematic fragments, the method of principal component analysis is used to reduce the dimension of the 13 kinematic feature parameters, and the first three principal components are classified by the improved ACO algorithm. The representative DC is obtained through the combination of the class of kinematic fragments. The analysis of the precision is also conducted. The results show that compared withK-means clustering algorithm and system clustering algorithm, the improved ACO algorithm can improve the precision of DC construction effectively.

principal component analysis; genetic variation; ant colony optimization(ACO); driving cycle(DC)

2016-03-03；

2016-04-28

国家自然科学基金资助项目(71431003)

刘炳姣(1991-),女,新疆乌鲁木齐人,合肥工业大学硕士生;石 琴(1963-),女,安徽蚌埠人,博士,合肥工业大学教授,博士生导师,通讯作者,E-mail:shiqing7081@sohu.com.

10.3969/j.issn.1003-5060.2017.10.001

U270.14

A

1003-5060(2017)10-1297-06

(责任编辑 胡亚敏)