压电纤维复合材料驱动的机翼动态形状控制

王晓明，周文雅＊，吴志刚，2

压电纤维复合材料驱动的机翼动态形状控制

王晓明1，周文雅2，＊，吴志刚1，2

1．大连理工大学 工程力学系 工业装备结构分析国家重点实验室，大连 116024 2．大连理工大学 航空航天学院，大连 116024

利用压电材料实现柔性机翼的主动形状控制，能够有效提高机翼结构效率和气动性能；要实现连续、光滑的高精确形状控制效果，机翼变形过程必须满足一定的动态要求。本文利用在上下翼面反对称铺设的新型压电纤维复合材料——宏纤维复合材料（MFC）提供驱动力矩，研究了机翼扭转变形的前馈轨迹跟踪控制。首先建立了机翼结构有限元模型和气动力载荷模型，采用载荷比拟法得到MFC作动器的控制载荷向量，给出了气动弹性控制方程及其状态空间表达形式。为跟踪预设的变形参考轨迹，以跟踪误差的时域积分为目标函数，对MFC作动器的电压加载历程进行了优化设计。结果表明，采用规划后的电压加载历程，机翼气动弹性响应很好地跟踪了预期参考轨迹，实现了连续、光滑的动态形状控制效果，提高了控制精度。

柔性机翼；压电纤维复合材料；宏纤维复合材料；气动弹性；前馈控制；二次规划

飞行器的飞行性能与机翼气动特性密切相关，根据飞行状态改变翼面形状以提高机翼气动效率和飞行性能是未来飞行器机翼设计的发展方向［1］；机翼形状主动控制技术也得到了广泛关注和研究［2－3］。传统的机翼形状控制是通过多个控制面的协调偏转实现的［4］。随着材料科学的发展，基于压电材料等智能材料的机翼主动形状控制成为研究热点。这种主动机翼的外形可以实现连续变化，能够最大限度提高机翼空气动力效率；而且可以简化翼面结构设计复杂性，省略舵机系统等附加机构，在降低结构重量的同时提高结构可靠性［5］。

传统压电材料具有变形量小、脆性大等缺点，限制了其使用范围和应用环境［6］。而压电纤维复合材料克服了上述缺点，能够提供较大驱动应变并具备较好柔韧性。此外，面内驱动的压电纤维复合材料因其各向异性特点，能够产生面内切应变，实现结构扭转或弯扭耦合控制［7］。赵寿根等［8］研究了压电纤维复合材料主动结构的变形模式和扭转特性。宏纤维复合材料（Macro Fiber Composites，MFC）［9］是目前较为先进的新型压电纤维复合材料。利用MFC等压电纤维复合材料实现机翼形状控制在国内外得到了广泛研究。Bilgen等［10］采用MFC作为机翼变形驱动器以实现无人机的滚转通道控制，并进行了风洞试验和飞行试验。李敏等［7］详细分析了不同纤维铺设方式下的机翼形状控制效果。张红艳等［11］利用MFC实现了旋翼桨叶模型的扭转控制，并进行了试验。

虽然利用MFC等压电纤维复合材料来改善气动弹性特性和提高飞行性能的可行性得到了理论上的证明，并在缩比机翼模型和小型飞行器上实现了相关试验验证；但尚未实现成熟的实际型号应用。一方面是受到几何尺寸、制造成本和环境适用性等方面的制约［5］；另一方面机翼变形过程涉及到结构、气动和控制之间的相互耦合，动力学特性复杂，为控制律设计增加了困难。在利用MFC等压电纤维复合材料实现机翼形状控制研究中，一般将变形过程作为静态或准静态过程进行分析，而没有考虑变形的动态过程，如驱动电压加载时间历程的影响。在实际应用过程中，往往采用阶跃或 斜 坡 等 电 压 加 载 方 式［10，12－13］，这 些 简单的电压输入形式往往会引起结构的瞬态和残余振动，严重影响控制效果和精度［13］；相关风洞和飞行试验也证明了这一点［10，14］。陆宇平和何真［15］指出机翼的形状控制不仅要求结构能够精确地达到某种曲面形状，还要求变形过程能够满足一定的动态性能；因而需要精确的动态形状控制，以实现连续的、光滑的变形。此外，在实际应用中机翼需要按预定程序变形［15］，以实现特定的机动；这就需要设计控制系统跟踪预期的变形轨迹。Kalaycioglu和Silva［13］的研究表明通过规划驱动电压随时间的加载历程可以减少结构的振动幅值。Schrock等［16］研究了MFC驱动的柔性板结构变形的前馈轨迹跟踪控制，但仅考虑了结构动力学，没有涉及结构与气动的耦合效应。在机翼形状控制研究领域，面向轨迹跟踪的动态形状控制的研究还相对较少。

在本文研究中，利用上下翼面反对称铺设的MFC材料为作动器，以提供驱动机翼扭转变形的控制扭矩。结合机翼结构有限元模型、气动力载荷和MFC控制载荷，给出了气动弹性控制方程及状态空间模型。利用二次规划方法对MFC作动器驱动电压加载历程进行了优化设计，以跟踪预设的机翼变形参考轨迹，实现连续、光滑的动态形状控制效果。最后，以某缩比大展弦比机翼模型为例，验证了本文控制方法的有效性。

1 数学模型

1．1 模型描述

铺设MFC作动器的机翼结构示意图如图1所示。机翼展长为L、弦长为W、厚度为H；MFC作动器的长度为l、宽度为w、厚度为h。作动器中线与机翼中线重合，其在机翼展向位置可用L1和L2表示。每组MFC作动器均采用上下表面反对称的铺设方式（纤维铺设角度相反）。如此通过施加同向电场，可产生驱动机翼产生扭转变形的控制扭矩。具体的驱动方式分析将在1．4节中给出。这种铺设方式的另一个好处是不会改变机翼弹性轴的位置［7］。

1．2 结构有限元模型

采用四节点板单元建立机翼的结构有限元模型。由于铺设的MFC材料会引起结构局部刚度和质量特性的改变，研究中结合复合材料层合板理论计算主动单元的刚度矩阵和质量矩阵［17］。通过组装得到总体刚度矩阵和质量矩阵，并考虑阻尼效应；柔性机翼的动力学方程可表示为

式中：x为节点位移向量；M＝Mb＋Ma和K＝Kb＋Ka分别为结构整体质量矩阵和刚度矩阵，其中下标b和a分别表示机翼基体材料层和MFC主动材料层对结构质量矩阵和刚度矩阵的贡献；C为阻尼矩阵，研究中采用Rayleigh阻尼假设；Q为空气动力载荷向量；F为MFC作动器提供的控制载荷向量。

1．3和1．4节将给出气动力载荷向量Q和MFC作动器的控制载荷向量F的表达式。

1．3 气动力载荷

基于Grossman准定常理论建立气动力模型［18］。不考虑机翼的弯曲变形，将气动力载荷等效到机翼弹性轴上，如图2所示。俯仰力矩表达式为

式中：Qm（）x为单位展长机翼绕弹性轴的抬头气动力矩；α（）x为扭转角（迎角）；ρ为空气密度；V为飞行速度；为升力系数；b为机翼半弦长；珔a为机翼弹性轴到中弦线之间的无量纲距离。

机翼展向的气动力分布采用“片条原理”计算［18］。因此，气动力载荷向量可表示为

式中：Cac和Kac为气动力影响系数矩阵。

1．4 MFC控制载荷

图3给出了机翼上下表面铺设MFC作动器的机翼局部示意图。对上下表面作动器施加同向电场，产生的驱动应力如图3（a）所示。可见，由于MFC纤维铺设方向是反对称的，能够产生驱动机翼扭转变形的扭矩，如图3（b）所示。图中Oxyz为机翼总体坐标系，O′123为上表面MFC材料的局部坐标系；其中1方向表示MFC纤维铺设方向（即材料主轴方向），与x方向夹角为θ（见图4（a））。MFC作动器产生的驱动应力以及控制载荷向量可利用载荷比拟法计算得到［19］。采用载荷比拟法能够大大降低有限元模型的自由度，且物理意义直观，非常适用于工程研究；在机翼等结构的变形和振动主动控制方面得到了应用［7，20－21］。

压电纤维复合材料总应变可分解为

式中：ε为总应变；εe和εE分别为弹性应变和压电应变；σ为应力；E为电场强度；s为恒电场强度下的柔度；d为压电应变常数矩阵。压电驱动的比拟应力和比拟载荷表达式为

式中：σs为比拟应力；Fs为等效比拟载荷；A为作动器有效面积；c为弹性矩阵。MFC作动器的厚度h远小于长度l和宽度w，因此厚度方向的应力σs3可设为零，从而简化为平面应力问题［7］。MFC材料的1－2平面为正交各向异性平面，其柔度矩阵为

在材料坐标系O′123下的面内比拟应力（如图4（b）所示）为

式中：εE1＝d11E1和εE2＝d12E1为面内压电应变；d11和d12为压电应变常数；E1为1方向（MFC材料极化方向）的电场强度。将式（8）展开可得

以上是在材料坐标系下计算得到的应力，利用材料力学中的“莫尔圆”［22］可计算出在机翼总体坐标系下的比拟应力σx、σy和τxy，如图4（c）所示。例如，上表面铺设的MFC作动器在L1处形成的扭矩可写为

综上，MFC作动器的控制载荷向量可表示为

式中：Fp为作动器单位电压产生的驱动力；u为加载电压向量，其维数与作动器组数相同。其中，每一组作动器包括上下表面反对称铺设的2片MFC作动器。

1．5 模型降阶与状态空间表达式

将气动力载荷向量表达式（式（3））和 MFC控制载荷向量表达式（式（12））代入式（1），并整理可得

由于有限元模型单元数、节点数较多，动力学方程式（13）阶数较高，不便于进行控制律设计。研究中采用模态截断法进行模型降阶［23］，引入式（14）所示的模态坐标变换。

式中：q为广义坐标向量；Φ为扭转振型矩阵。将式（14）代入式（13），在公式两端左乘ΦT；并进一步整理可得

为便于设计控制器，将系统模型表示为状态空间形式为

式中：X＝ qTq［］TT为状态变量；y为控制输出。系统矩阵和控制输入矩阵的表达式为

设n为被控模态数，m为MFC作动器组数，则X和u分别为维数为2n×1和m×1的向量，A和B分别为维数为2n×2n和2n×m的矩阵。

系统的控制输出y以及输出矩阵Cy可根据不同任务或者控制目标而设定，如可将控制输出y选择为机翼的翼尖扭转角度或翼面升力增量等；其中翼面变形引起的升力增量计算公式为

2 机翼动态形状前馈跟踪控制器设计

设计跟踪控制器的目的是希望机翼形状的变化能够跟踪预设的参考轨迹，实现连续、光滑的动态变形过程，满足特定任务需求，如：按一定规律增加升力，实现特定的横滚机动，修正机翼形状误差等。

跟踪控制器的设计可转化为一个优化问题，即通过设计最优控制输入，使得实际控制输出与预设的参考输出轨迹之间的误差最小。

2．1 优化问题提法

具有一般性的前馈跟踪控制问题可以描述为：寻求最优控制输入式（20），使得式（21）的二次型目标函数（性能指标）取得极小值。

式中：yr为预先给定的参考输出轨迹；珚Q和R为加权矩阵。目标函数中的第1项表征实际输出与参考输出之间的跟踪误差，第2项表征控制能量。式（21）可展开为

此外，设计变量和目标函数受到系统动力学方程、初边值条件以及MFC电压限制等条件的约束。约束方程可表示为

式中：X0为系统初始状态；umin和umax为 MFC作动器允许可用的最小和最大加载电压。

2．2 优化方法

式（20）、式（21）和式（23）给出了优化问题的三要素：设计变量、目标函数和约束条件。求解上述优化问题可利用多种优化算法。该优化问题的目标函数是系统状态和输入的二次型积分表达式，约束条件为线性约束；针对该特点，本研究将采用非线性规划理论中的二次规划方法对优化问题进行求解。首先将目标函数（积分形式）和系统方程（微分形式）在时间域上采用有限差分法离散；从而将目标函数和动力学方程转化为代数表达式。进而采用二次规划方法进行求解，使得目标函数极小化，并给出对应的最优控制输入。优化过程需要考虑不等式约束，因此本文采用二次规划理论中的“有效集”算法进行求解［24］。

3 算例与结果分析

3．1 算例介绍

本文以文献［7］给出的大展弦比机翼缩比模型为例验证第2节动态形状控制算法的有效性；算例中机翼和MFC作动器的参数如表1所示。共铺设2组MFC作动器，上下表面的纤维铺设角度分别为＋45°、－45°。结构阻尼比设为0．02，用于计算Rayleigh阻尼比例系数。飞行状态设定为：飞行速度V＝120m／s，空气密度ρ＝0．088 9kg／m3（飞行高度为20km）。

仿真中，首先以翼尖扭转角为控制输出。设机翼初始为未变形状态，初始控制输入为零，即X0＝0，u0＝0。期望通过控制作用使机翼的翼尖扭和式（17）可求出达到期望控制输出所需的MFC作动器稳态电压值为uf＝［379．1 531．8］TV。值得一提的是，如果不考虑气动力载荷的作用，即令Q＝0，则所需电压值为［424．9 597．7］TV；这体现了气动弹性效应的影响。

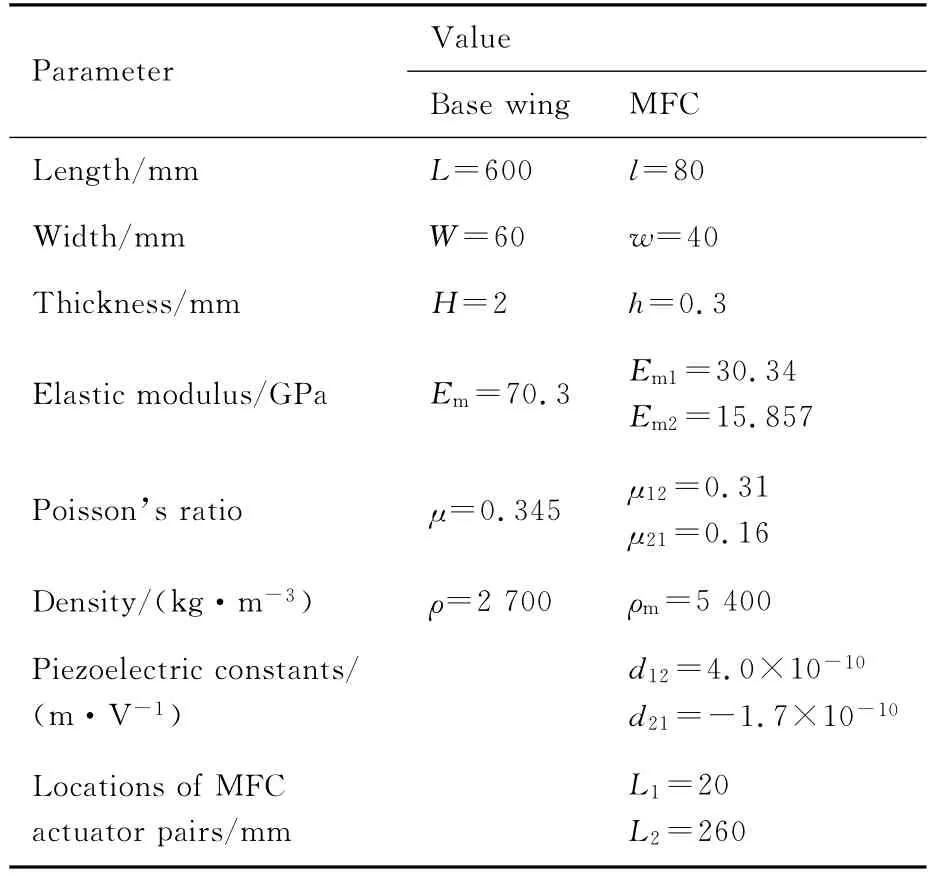
表1 仿真中机翼与MFC作动器的参数Table 1 Parameters of wing and MFC actuators in simulations

如前所述，MFC作动器电压加载的时间历程（电压值从u0加载到uf的过程）对机翼变形过程的动态响应有较大影响。图5给出了机翼翼尖扭转角和翼面升力在斜坡电压加载历程下的响应曲线。在这种加载方式下，机翼达到目标形状后仍存在残余振动。虽然机翼的振动幅值在阻尼作用下会逐渐衰减，但所需时间较长；短时间内机翼振动得不到有效抑制。文献［10］进行了利用MFC驱动机翼变形实现小型飞行器飞行控制的试验；试验中采用了阶跃输入信号。文章中指出施加电压后机翼产生了低频的扭转振动，导致明显降低了实际控制效果。因此如果在实际应用中采用这类简单的电压加载方式，容易导致机翼振动和气动力波动的问题。机翼振动会严重降低形状控制精度，引起结构的强度和疲劳问题；而气动力的波动会对飞行器飞行稳定性造成不利影响。

3．2 机翼动态形状控制

为实现连续、光滑的动态形状控制过程，提高控制精度，图6给出了一条预先设计的控制输出参考轨迹。跟踪该参考轨迹有两个作用：① 实现特定的动态控制目标，达到所需控制性能；② 抑制机翼在形状控制过程中的瞬态和残余振动。

利用第2节给出的前馈跟踪控制方法，可以规划出实现跟踪图6给出的参考轨迹所需的最优控制输入，如图7（a）所示。在最优控制输入作用下，机翼翼尖扭转角的响应曲线如图7（b）所示。

可以看出，在二次规划方法优化设计得到的MFC作动器最优电压加载历程下，机翼形状的变化过程很好地跟踪了预设参考轨迹；且没有产生明显的瞬态和残余振动，实现了连续、光滑的形状控制效果。

增加升力以提高飞行器气动性能是机翼主动形状控制的重要目的之一［6］。下面以翼面升力增量为控制输出给出机翼动态形状控制效果。为满足飞行机动的需要，假设需要翼面升力按图8给出的参考轨迹规律增加。

利用第2节给出的前馈跟踪控制算法，可以计算出跟踪预期升力变化轨迹所需的最优控制输入如图9（a）所示，跟踪控制效果如图9（b）所示。

可以看出，利用优化设计得到了MFC作动器最优电压加载历程，翼面升力的变化过程很好地跟踪了预设的参考轨迹。气动力没有产生明显波动，这对于飞行器的飞行稳定性具有重要作用。

对比图5、图7和图9，在利用压电纤维复合材料实现机翼形状控制过程中，不仅需要机翼能够精确地达到某个形状，还须满足一定的动态性能。利用本文的前馈跟踪控制算法，可以规划出最优电压加载历程，实现较好的轨迹跟踪控制，可以提高机翼动态形状控制效果和飞行器飞行性能。

4 结 论

1）利用MFC材料面内驱动的各向异性特点，在机翼上下表面反对称铺设MFC作动器可实现机翼的扭转控制。

2）建立了MFC驱动的机翼气动弹性主动控制方程；仿真结果表明，不合理的电压加载方式会引起机翼瞬态和残余振动，影响形状控制效果。

3）基于给定的预设控制输出参考轨迹，利用二次规划方法，通过优化设计得到了最优电压控制输入信号，较好地跟踪了参考轨迹，实现了连续、光滑的机翼动态形状控制效果。

［1］ SOFLA A Y N，MEGUID S A，TAN K T，et al．Shape morphing of aircraft wing：Status and challenges［J］．Materials ＆ Design，2010，31（3）：1284－1292．

［2］ 冷劲松，孙健，刘彦菊．智能材料和结构在变体飞行器上的应用现状与前景展望［J］．航空学报，2014，35（1）：29－45．LENG J S，SUN J，LIU Y J．Application status and future prospect of smart material and structures in morphing aircraf［J］．Acta Aeronautica et Astronautica Sinica，2014，35（1）：29－45（in Chinese）．

［3］ 杨超，陈桂彬．主动气动弹性机翼技术分析［J］．北京航空航天大学学报，1999，25（2）：171－175．YANG C，CHEN G B．Analysis of active aeroelastic wing technolog［J］．Journal of Beijing University of Aeronautics and Astronautics，1999，25（2）：171－175（in Chinese）．

［4］ KUDVA J N，MARTIN C A，SCHERER L B，et al．Overview of the DARPA／AFRL／NASA smart wing program［C］／Proceedings of the 1999Symposium on Smart Structures and Materials．Bellingham，WA：International Society for Optics and Photonics，SPIE，1999：230－236．

［5］ 李敏，陈伟民，贾丽杰．压电驱动器的气动弹性应用［J］．航空学报，2009，30（12）：2301－2310．LI M，CHEN W M，JIA L J．Application of piezoelectric actuators to aircraft aeroelastic performance enhancement［J］．Acta Aeronautica et Astronautica Sinica，2009，30（12）：2301－2310（in Chinese）．

［6］ 李继威，张勇，陈继春．压电材料在飞行翼形控制方面的一些应用［J］．电子元件与材料，2009，28（6）：74－78．LI J W，ZHANG Y，CHEN J C．Application to control airfoil of aerocraft using piezoelectric materials［J］．Electronic Components and Materials，2009，28（6）：74－78（in Chinese）．

［7］ 李敏，陈伟民，贾丽杰．压电纤维复合材料铺层用于翼面设计的驱动特性与刚度影响［J］．航空学报，2010，31（2）：418－425．LI M，CHEN W M，JIA L J．Drive characteristics and stiffness influence with piezoelectric fiber composite actuators on airfoil surface［J］．Acta Aeronautica et Astronautica Sinica，2010，31（2）：418－425（in Chinese）．

［8］ 赵寿根，程伟，管德．1－3型压电纤维主动叠层板扭转特性的研究［J］．航空学报，2006，27（4）：624－629．ZHAO S G，CHENG W，GUAN D．Torsion characteristics of active laminates with 1－3PFC layers［J］．Acta Aeronautica et Astronautica Sinica，2006，27（4）：624－629（in Chinese）．

［9］ WILLIAMS R B，PARK G，INMAN D J，et al．An overview of composite actuators with piezoceramic fibers［C］／Proceedings of IMAC－XX：A Conference on Structural Dynamics．Bellingham，WA：SPIE，2002：421－427．

［10］ BILGEN O，KOCHERSBERGER K，DIGGS E C，et al．Morphing wing aerodynamic control via macro－fiber－composite actuators in an unmanned aircraft［C］／Proceedings of the 2007AIAA InfoTech at Aerospace Conference．Reston：AIAA，2007：303－319．

［11］ 张红艳，白长青，沈亚鹏．粗纤维压电复合材料（MFC）对旋翼桨叶模型扭转控制的实验及数值研究［J］．应用力学学报，2009，26（3）：456－460．ZHANG H Y，BAI C Q，SHEN Y P．Experimental and numerical analysis for twist control of rotor blade model with macro fiber composite（MFC）［J］．Chinese Journal of Applied Mechanics，2009，26（3）：456－460（in Chinese）．

［12］ 脱朝智，钱卫，杨睿．主动压电纤维的驱动仿真与试验研究［C］／第十二届全国空气弹性学术交流会论文集．北京：中国空气动力学学会，中国力学学会，2011：581－586．TUO Z Z，QIAN W，YANG R．Simulation and experimental study on the active piezoelectric fiber driver［C］／Proceedings of the 12th National Aeroelasticity Academic Communication．Beijing：Chinese Aerodynamics Research Society，The Chinese Society of Theoretical and Applied Mechanics，2011：581－586（in Chinese）．

［13］ KALAYCIOGLU S，SILVA D．Minimization of vibration of spacecraft appendages during shape control using smart structures［J］．Journal of Guidance Control and Dynamics，2000，23（3）：558－561．

［14］ LI M，CHEN W M，GUAN D．Improvement of aircraft rolling power by use of piezoelectric actuators［J］．Chinese Journal of Aeronautics，2004，17（2）：87－92．

［15］ 陆宇平，何真．变体飞行器控制系统综述［J］．航空学报，2009，30（10）：1906－1911．LU Y P，HE Z．A survey of morphing aircraft control systems［J］．Acta Aeronautica et Astronautica Sinica，2009，30（10）：1906－1911（in Chinese）．

［16］ SCHROCK J，MEURER T，KUGI A．Motion planning for piezo－actuated flexible structures：Modeling，design，and experiment［J］．IEEE Transactions on Control Systems Technology，2013，21（3）：807－819．

［17］ 沈观林，胡更开．复合材料力学［M］．北京：清华大学出版社，2006：202－204．SHEN G L，HU G K．Mechanics of composite materials［M］．Beijing：Tsinghua University Press，2006：202－204（in Chinese）．

［18］ 杨超，吴志刚，万志强．飞行器气动弹性原理［M］．北京：北京航空航天大学出版社，2011：52－54．YANG C，WU Z G，WAN Z Q．Aeroelasticity principle of aircraft［M］．Beijing：Beihang Press，2011：52－54（in Chinese）．

［19］ 李敏，陈伟民，王明春，等．压电驱动的载荷比拟方法［J］．中 国 科 学 （E 辑：技 术 科 学），2009，39（11）：1810－1817．LI M，CHEN W M，WANG M C，et al．A load simulation method of piezoelectric actuator in FEM for smart structures［J］．Science in China（Series E：Technological Sciences），2009，39（11）：1810－1817（in Chinese）．

［20］ 高仁璟，张莹，吴书豪，等．面向结构形状控制的驱动器结构参数与控制电压协同优化设计［J］．光学精密工程，2014，22（6）：1538－1546．GAO R J，ZHANG Y，WU S H，et al．Integrated design optimization of actuator structural parameters and control voltages for morphing structural shapes［J］．Optics and Precision Engineering，2014，22（6）：1538－1546（in Chinese）．

［21］ 孙杰，李敏，张骞．垂直尾翼抖振的压电主动控制研究［C］／北京力学会第20届学术年会论文集．北京：中国力学学会，2014．SUN J，LI M，ZHANG Q．Piezoelectric active control of vertical tail buffeting［C］／Proceedings of the 20th Annual Seminar of the Beijing Society of Theoretical and Applied Mechanics．Beijing：The Chinese Society of Theoretical and Applied Mechanics，2014（in Chinese）．

［22］ 单辉祖．材料力学教程［M］．北京：高等教育出版社，2004：202－204．SHAN H Z．Material mechanics course［M］．Beijing：Higher Education Press，2004：202－204（in Chinese）．

［23］ FORSTER E E，YANG H T Y．Flutter control of wing boxes using piezoelectric actuators［J］．Journal of Aircraft，1998，35（6）：949－957．

［24］ 陈宝林．最优化理论与算法［M］．北京：清华大学出版社，2005：417－422．CHEN B L．Theory and algorithms of optimization［M］．Beijing：Tsinghua University Press，2005：417－422 （in Chinese）．

Dynamic shape control of wings using piezoelectric fiber composite materials

WANG Xiaoming1，ZHOU Wenya2，＊，WU Zhigang1，2
1．State Key Laboratory of Structural Analysis for Industrial Equipment，Department of Engineering Mechanics，Dalian University of Technology，Dalian 116024，China
2．School of Aeronautics and Astronautics，Dalian University of Technology，Dalian 116024，China

The structure efficiency and aerodynamic performance of flexible wings can be effectively improved with active shape control using piezoelectric materials．In order to realize the effect of continuous smooth dynamic shape control with high precision，some dynamical requirements must be satisfied in shape control process of the wings．In this study，new piezoelectric fiber composite materials—macro fiber composite（MFC），which are laid anti－symmetrically on the top and bottom wing surfaces，are used for actuation to achieve feedforward tracking control of twist motion of the wing．The structural finite element model for the wing and the aerodynamic loads are established．The control input vector for the MFC is obtained using load simulation method．The active aeroelastic equations and the state space representation are presented．In order to track the pre－defined deformation reference trajectory，the voltage profiles for MFC actuators are optimized with time－domain integration of tracking errors being chosen as the objective function．The simulation results show that the aeroelastic responses of the wing follow the prospective reference trajectory well with application of the optimal voltage profiles．Continuous smooth dynamic shape control effect has been realized，and control precision has been improved．

flexible wings；piezoelectric fiber composite materials；MFC；aeroelasticity；feedforward control；quadratic programming

2016－04－11；Revised：2016－05－15；Accepted：2016－07－06；Published online：2016－07－21 08：39

URL：www．cnki．net／kcms／detail／11．1929．V．20160721．0839．002．html

s：National Natural Science Foundation of China（11432010，11502041）

V214．3

A

1000－6893（2017）01－220313－09

http：／hkxb．buaa．edu．cn hkxb＠buaa．edu．cn

10．7527／S1000－6893．2016．0207

2016－04－11；退修日期：2016－05－15；录用日期：2016－07－06；网络出版时间：2016－07－21 08：39

www．cnki．net／kcms／detail／11．1929．V．20160721．0839．002．html

国家自然科学基金 （11432010，11502041）

＊通讯作者 ．E－mail：zwy＠dlut．edu．cn

王晓明，周文雅，吴志刚．压电纤维复合材料驱动的机翼动态形状控制［J］．航空学报，2017，38（1）：220313．WANG X M，ZHOU W Y，WU Z G．Dynamic shape control of wings using piezoelectric fiber composite materials［J］．Acta Aeronautica et Astronautica Sinica，2017，38（1）：220313．

（责任编辑：徐晓）

＊Corresponding author．E－mail：zwy＠dlut．edu．cn